In this document, one presents the manual of FeResPost.
When sizing a structure with FE software, the engineer is often lead to use or develop tools that automate the computation of margins of safety, reserve factors or other results from outputs obtained with a FE solver. Then the engineer is facing several problems:
He has to take into account the possibility of modifications of the structure and of its corresponding finite element model during the project.
Also, the allowables may change during the course of the project.
Sometimes, the calculation methods are imposed by a client or a methodology department in the company, and these methods may also be modified, or be defined concurrently with the sizing activities.
For long duration projects, the members of the calculation team are often displaced as the work proceeds, and time is lost to transfer the information from one engineer to another.
All these problems induce difficulties in the management of the automated post-processing. These must be as simple and cleanly written as possible to allow an easy understanding by everyone. Also their architecture must be flexible to make the modifications easy to implement and reduce the risk of errors.
The problems mentioned above are very similar to the kind of problems a programmer is facing when writing a large program. To help the programmer in this task, the object-orientation has emerged as a new programming language concept. Object-oriented languages allow the development of more flexible programs with a better architecture and allow the re-usability of code. Many object-oriented languages are now available. They can be compiled languages (C++, Fortran 90,...) or interpreted ones (Ruby, Python, Visual Basic,...).
FeResPost is a compiled library devoted to the programming of automated post-processing of finite element results. It provides the definition of several classes and one module. It uses object orientation at two levels:
With object-oriented languages, it allows to write interpreted and object-oriented automated post-processing. An example of such an object-oriented post-processing program is given in Chapter IV.4.
The FeResPost library is mainly written in C++, which is also an object-oriented language. Then a Ruby wrapping is provided around the C++ code.
During the development of FeResPost, the developer has been trying to maintain as much as possible the simplicity and clarity of the language in which post-processing programs are written.
FeResPost can be accessed from different languages and on different platforms:
As a ruby extension. Binaries are available for Windows and Linux distributions of ruby.
As a Python copiled library on Windows and Linux.
As a COM component on Windows. Then, the library can be used with different languages that support COM interface: C, C++, ruby, Python, VBA...
As a .NET assembly that allows the programming with VB.NET, C++.NET, C#...
One gives here some advice to people starting to use FeResPost. The order in which the knowledge is acquired matters. One of the worst way to try to learn FeResPost is to read the manual while writing bits of code meant to solve the particular problem the user has in mind. Instead, one suggests the following sequence of knowledge acquisition:
FeResPost is an extension of ruby programming language. This means that the examples provided in the document are small ruby programs. Therefore a basic knowledge of ruby is necessary. People trying to learn ruby and FeResPost at the same time will probably fail in both tasks.
Very good books on ruby language are available in libraries. Internet resources are also a source of information (newsgroups, tutorials with examples...).
Note that people already familiar with one or several object-oriented programming languages will have no difficulty to acquire a basic knowledge of ruby.
Then, the user may test FeResPost by running the small examples. These are provided in the sub-directories in “RUBY” directory. Note that the Nastran bdf files should first be run in order to have the op2 result files available. It may be a good idea to try first to understand the structure of the bdf files and of the organization of the finite element model.
The small examples are meant to be increasingly difficult. So, the user should first run the examples in “EX01” directory, then in “EX02”... For each example, every statement should be understood, and the corresponding pages of the user manual should be carefully read.
When all the small examples have been run and understood, the user will probably have acquired a reasonable understanding of the various capabilities of FeResPost. Then it may be a good idea to start to read the user manual. For example, to read a few pages each day in such a way that the information can be digested efficiently.
The two examples “PROJECTa” and “PROJECTb” illustrate the programming of more complex post-processing of Results involving loops on load-cases, on several types of post-processing calculations... These two projects should be studied at the very end.
“PROJECTa” is meant to be studied before “PROJECTb”. Indeed, “PROJECTa” is easier to understand than “PROJECTb”, because it is less object-oriented. but it is also less complete and less nice from a programming point of view.
The reason why the advices above is given is that many users send mails of questions or complaints because they fail to understand something about FeResPost which is clearly illustrated in the examples. Sometimes, the problems faced by the users are simply related to a lack of understanding of the ruby programming language.
This document is organized as follows:
In Part I one presents the various classes defined in FeResPost library, and their member functions. One emphasizes the definition of the concepts to which they correspond, and their relevance for the developments of post-processing tools.
Part II is devoted to the presentation of the classes devoted to composite calculations with the Classical Laminate Analysis Theory.
Part III is devoted to the presentations of the preferences for the different solvers supported by FeResPost.
In Part IV, several examples of post-processing written with the ruby library are presented.
Part VI contains the description of FeResPost COM component. This Part is less detailed as most methods in COM component have the same characteristics as the corresponding methods in ruby extension.
Examples of programs with the COM component are given in Part VII.
Part VIII contains the description of FeResPost NET assembly. Here again, the description is shortet than for the ruby extension.
Examples of programs with the NET assembly are given in Part IX.
Part V contains the description of FeResPost Python library. Both the library and the examples are described in that part which is vry short as the Python and ruby languages are very similar.
Part X contains the annexes.
References are given in Part XI.
A list of the different classes defined in FeResPost with pointers to Tables listing the methods defined by these classes is given in Table 1.
| Class | Chapter | Table | Page |
| “Common” Classes | |||
| DataBase | I.1 | I.1.1 | 52 |
| CoordSys | I.2 | I.2.1 | 79 |
| Group | I.3 | I.3.1 | 91 |
| Result | I.4 | I.4.1 | 100 |
| ResKeyList | I.5 | I.5.1 | 179 |
| Post (module) | I.6 | I.6.1 | 186 |
| Classical Laminate Analysis
| |||
| ClaDb | II.2 | II.2.1 | 459 |
| ClaMat | II.3 | II.3.1 | 468 |
| ClaLam | II.4 | II.4.1 | 478 |
| ClaLoad | II.5 | II.5.1 | 513 |
| Solver Preferences
| |||
| NastranDb | III.1 | III.1.1 | 534 |
| SamcefDb | III.2 | III.2.1 | 670 |
FeResPost is still at the very beginning of its development and much work is still necessary to cover a wider range of applications. One gives below a few examples of possible improvements, more or less sorted by order of emergency or facility:
Correction of bugs...
Addition of specialized post-processing modules programmed at C++ level to provide efficiency. For examples:
A module devoted to fatigue and damage tolerance analysis.
A module devoted to the calculation of stresses in bar cross-sections from the bar forces and moments.
...
Extension of FeResPost by providing interfaces towards other FE software like Abaqus,...
...
Of course, we are open to constructive remarks and comments about the ruby library in order to improve it.
.NET515–527, 531–535
Abaqus6
abbreviations47–48, 314
Acceleration of computation118–119, 361–362, 575–585, 608
asef317
Autodesk266, 697
Bacon313, 314, 495
bacon314
banque313–314
BBBTsee Binary Blocked Balanced Tree, see Binary Blocked Balanced Tree
big endian275–277
Binary Blocked Balanced Tree270
BLOB65, 101, 115, 381–383, 436, 473, 492, 497–498, 500–501, 535
bolt group621
bolt group(617
bridge609–615
C467
C++62, 67, 70, 465–466
CLA449–450, 521–522
ClaDb125, 203–208, 449, 521
ClaLam125, 217–235, 450, 522
ClaLoad125, 237–243, 450, 522
ClaMat125, 209–215, 449–450, 521
Classical Laminate Analysis449–450, 521–522
code327–330
COM441–455, 459–512, 609
Combined strain criterion182
Complex, Complex98–100
Component Object Model441–455, 459–512
Composite48–49, 125–243
CoordSys35, 53–59, 263–264, 314–315, 366
COPYING623–637
CRMS296
DataBase35, 37–52, 92–94
DataBase, flags, readDesFac318
DataBase, flags, readDesFac318
DataBase, key43–44
des316–324
disable269, 276, 318
dynam317
ECMAScript268
EDS266, 268
enable269, 276, 318
endiannes275–277
EQEXINE286
EQEXING286
Equivalent Strain134, 166, 181, 182
ESAComp125, 207
excel413–415, 423, 425–426, 443, 472–473, 475–489, 491–512, 609–615
exception119, 433, 447
fac316–324
FEM265
FeResPost35
Fick199
FieldCS73, 75, 93, 366
finite elements35
Fourrier195
General Public License623–637
Gmsh50–52, 381, 492–495, 497–498, 500–501, 577
GNU543
GPL623–637
Group35, 37, 41–43, 61–66, 80, 109, 264–265, 315–316, 354–357
Hash Key271
Hashin criteria189–191
HD5119, 389–390, 395–396, 435–436
HDF119, 257–259, 288–293, 389–390, 395–396, 435–436, 542
HKsee Hash Key, see Hash Key
Hoffman criterion186
Honeycomb criterion193–194
I-DEAS266, 268
identifier125
IDispatch444, 466
Ilss criterion194–195
Ilss_b criterion194–195
include256
instance method436, 605
Inventor Nastran266, 697
iterator49–50, 65, 101–102, 107–108, 293–294, 325
iterators357–358
keysee DataBase, key, see Result, key
lambda436
layersee Result, layer
Lesser General Public License623–637
LGPL623–637
little endian275–277
Makefile542
Maximum strain criterion181–182
Maximum stress criterion180
mecano317
Mechanical Strain134, 166, 181, 182
Microsoft444, 466
Microsoft Office414, 425–426
MINGW543
Mohr83, 84
MSYS543
Nastran64, 198, 249–309, 335
NET515–527, 531–535
NX314
op2257–259, 265–269, 295–309, 392–393
Patran35, 41, 42, 61, 63, 97, 307, 344
Post35, 81, 89, 109–119
post-processing35
Predefined criterion118–119, 361–362, 575–585, 608
proc436, 604
PSD115–118, 296, 371–372
Puck criterion187
Puck_b criterion187–188
Puck_c criterion188
Python431–437
python461–463
random115–118, 270
random access277–288, 319–324
Regular expression267–269
Reserve Factor176
ResKeyList35, 71, 76, 78, 79, 105–108
Result35, 37, 38, 43–47, 67–103, 105, 109, 112, 119, 270–293, 295–309, 319–324, 358–372
Result, Complex98–100
Result, key70–71, 76, 79, 94, 100–102, 105, 108, 360
Result, layer70–71
Result, value44, 70, 73–74, 79, 100–102
Results563–571
results35
rfalter256
rfinclude256
RMSINT117
ruby35, 67, 464
Samcef47, 311–331, 483, 489, 492, 494–496
scalar73, 78, 79, 81–84, 87, 92, 94, 96, 97, 100
Siemens314
SQL65, 101, 115, 381–383, 436, 473, 492, 497–498, 500–501, 535
SQLite381–383, 436, 473, 492, 497–498, 500–501, 535
stabi317
Strength Ratio176
superelement257–259, 390–396
tensorial73, 83–85, 87, 92, 94, 100
Tresca criterion178–179
Tsai-Hill criterion183–184
Tsai-Wu criterion184–186
tuple432, 436
Unigraphics266, 268
valuesee Result, value
VBA413, 443, 472–473, 475–489, 491–512, 609–615
VBA-Ruby bridge609–615
VBscript464
vectorial73, 82, 83, 87, 92, 94, 100
Von Mises83, 84
Von Mises criterion179
word414, 425–426
xdb257–259, 270–288, 295–309, 393–395, 435–436
Yamada-Sun criterion192
FeResPost is a library that allows the manipulation of finite element entities and results. Its purpose is to ease the development of post-processing programs. The supported solvers and corresponding program preferences are discussed in Part III of the document.
The various capabilities implemented in the ruby extension are mainly inspired by Patran capabilities. Several types of objects can be manipulated:
The “DataBase” class corresponds to the Patran concept of dataBase. It is used to store the finite element model definition, the results, the groups,... It also allows to perform operations on the corresponding objects. This class is presented in Chapter I.1.
The “CoordSys” class allows the definition and manipulation of coordinate systems. This class is very practical for some manipulation of Results. It is presented in Chapter I.2.
The “Group” class corresponds to the Patran “group”. This class is presented in Chapter I.3.
The “Result” class is used to retrieve, store, transform finite element results. This class is presented in Chapter I.4.
The “ResKeyList” class is very useful to define lists of entities on which results are to be retrieved. This class is presented in Chapter I.5. Actually, this class is still under construction. However, the ResKeyList objects are already used for the manipulation of Results (section I.4.3).
Finally, additional functions, not member of any class are defined in a module called “Post”. “Post” module is discussed in chapter I.6. In the same chapter one also discusses other topics, as exceptions.
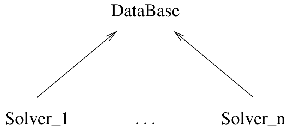
Basically, a “DataBase” class is a container used to store a finite element model, Groups, Results, and other less important entities. The DataBase class also allow to retrieve, manipulate or modify these objects. The DataBase class is a generic class that cannot be instantiated. The specialized classes that inherit the generic DataBase class are described in Part III. Other solvers might be supported in the future. The class hierarchy is schematically represented in Figure I.1.1.
As three classes are represented in Figure I.1.1, the methods described in this Chapter may belong to the generic DataBase class or to the derived classes. A few basic principles should help the user to “guess” in which class some of the methods are defined:
All methods related to the definition of the model stored in the DataBase are defined in the specialized classes.
All methods related to the reading of Results from solvers output files are defined in the specialized classes.
Most methods for the manipulation of Groups and of Results are defined in the generic “DataBase” class.
Throughout the Chapter one specifies for the different methods, in which class they are defined. This Chapter is divided in several sections:
One presents in section I.1.1 the methods devoted to the initialization of the finite element model in the DataBase.
Section I.1.2 is devoted to the DataBase’s methods devoted to the manipulation of Groups.
Section I.1.3 is devoted to the DataBase’s methods devoted to the manipulation of Results.
In section I.1.4, the manipulation of abbreviations stored in the DataBase is described.
The interaction of CLA classes with DataBase classes is discussed in section I.1.5.
The iterators of Class DataBase are described in section I.1.6.
Finally, general purpose methods are presented in section I.1.7.
A list of the methods defined in “DataBase” class is given in Table I.1.1.
No generic “DataBase” object can be created because “DataBase” class cannot be instantiated. This means that a statement like:
db=DataBase.new()
leads to an error message. All the methods described in this section are defined in the specialized versions of the DataBase class. So no “new”, “initialize” or “clone” method is defined in DataBase class.
One defines three methods that allow to retrieve the number of entities of certain types stored in DataBase FE model:
“NbrCoordSys” attribute returns the number of coordinate systems stored in the DataBase.
“NbrElements” attribute returns the number of elements stored in the DataBase.
“NbrNodes” attribute returns the number of nodes stored in the DataBase.
Each of these methods has no argument and returns an integer. Other methods allow to check the existence of finite element entities:
“checkCoordSysExists” returns true if the specified coordinate system exists, false otherwise.
“checkElementExists” returns true if the specified element exists, false otherwise.
“checkNodeExists” returns true if the specified node exists, false otherwise.
“checkRbeExists” returns true if the specified RBE exists, false otherwise.
Each of these four methods has one integer argument corresponding to the entity the existence of which is checked.
Several methods allow to retrieve elements information. Each of the following methods has one integer argument corresponding to the element ID:
“getElementType” returns an integer corresponding to the type ID of the element.
“getElementTypeName” returns a string corresponding to the type name of the element.
“getElementDim” returns an integer corresponding to the topological dimension of the element.
“getElementNbrNodes” returns an integer corresponding to the number of nodes defining the element.
“getElementNbrCornerNodes” returns an integer corresponding to the number of corner nodes defining the element.
“getElementNodes” returns an array of integers that corresponds to the element nodes.
“getElementCornerNodes” returns an array of integers that corresponds to the element corner nodes.
Normally one class corresponds to each solver supported by FeResPost. The preferences for the different supported solvers are described in Part III.
Groups can be stored in, and retrieved from a DataBase object. One presents here the methods defined in generic class DataBase, or in its derived classes, and that are devoted to the manipulation of Group objects. In the DataBase, the Group objects are stored in a mapping associating their names to the Group. This association allows to retrieve the Group when needed.
One makes the distinction between the simple manipulation of Groups described in section I.1.2.1 and the more complicated operation where new Groups are created by association operations (section I.1.2.2). The methods related to these associative operations are often defined in the specialized versions of the Database class.
One describes here methods that allow the manipulation of Groups stored in a generic DataBase object. All the methods described in this section are defined in generic DataBase class. These methods are described below:
“readGroupsFromPatranSession” reads one or several Groups from a Patran session file obtained using the utility “Patran–>utilities–>groups–>exportToSessionFile”. The argument is a String corresponding to the name of the session file. The method returns nil. If some of the entities read in the session file do not exist (for example, missing elements or nodes), then the read entities will not be added to the Group. This corresponds to the behavior of Groups in Patran. Therefore the session file containing the definition of Groups should be read after the finite element model.
Note that, even though the method is related to an MSC software, it can be used with DataBase related to different solvers. This is the reason why the method “readGroupsFromPatranSession” is defined in generic DataBase class.
The method “readGroupsFromPatranSession” works as follows:
It searches in the file the statements “ga_group_entity_add” and stores the while PCL statement in a string.
Then, the name of the Group being initialized is scanned from the string.
Finally, the entity definition is scanned:
The statement searches words like “Node”, “Element”, “MPC”, “CoordSys”. Note that “MPC” corresponds to the definition of a list of rigid body elements (RBEs). Nastran MPC cards cannot be inserted in a Group.
For any of the four first words, the method builds a list of integers corresponding to the identifiers of the entities to be added to the Group. For the three last words above, the method skips the entities.
The entities can be defined by a list of integers separated by blanks, or by pairs of integers separated by “:” which defines a range of integers, or by groups of three integers separated by two “:” which defines a range with a stepping argument.
Prior to storing the Group in DataBase, the method checks that the entities of the Group are defined in the DataBase. If not, the are erased from the Group.
Note that the definition of Groups in Ruby by range specification uses the same kind of formats as ”setEntities” method in Group class. (See section I.3.3.)
“writeGroupsToPatranSession” writes the Groups stored in the DataBase in a text file corresponding to a Patran session defining groups. This method is the reverse of method “readGroupsFromPatranSession” an has one argument: the name of the Patran session file. Note that “MPC” corresponds to the definition of a list of rigid body elements (RBEs). Nastran MPC cards cannot be inserted in a Group.
“addGroupCopy” is used to add a Group to a DataBase. The method returns nil and has one argument: the Group object. Note that, when adding a Group to the DataBase, a check is done to verify that all its entities are present in the DataBase. If not present, then the corresponding entities are erased from the Group. As this involves the modification of the Group definition, all operations are performed on a copy of the Group argument. In the DataBase, the added Group is associated to the name of the group argument. If a Group associated to the same name existed prior to adding the new Group, the method replaces the former Group by the new one.
“NbrGroups” attribute has no argument and returns the number of Groups stored in the DataBase.
“getAllGroupNames” has no argument and returns an Array of String objects corresponding to the names of all the Groups contained in the DataBase on which the method is called.
“checkGroupExists” allows to check whether a Group exists in the DataBase. The argument is a String object corresponding to the name of the Group. The returned value is true if the Group has been found, false otherwise.
“getGroupCopy” has one argument: a String object corresponding to the name of the Group one tries to retrieve. The method returns a copy of the Group stored in the DataBase, if the Group with the appropriate name exists. The method returns an error is no Group with the appropriate name exists in the DataBase.
“eraseGroup” erases a Group from the DataBase. The argument is a String object corresponding to the name of the Group to be erased. If the Group does not exist in the DataBase, nothing is done.
“eraseAllGroups” erases all Groups stored in the DataBase. This method has no argument.
“getGroupAllElements” returns a Group containing all the elements that define the model stored in the DataBase.
“getGroupAllNodes” returns a Group containing all the nodes that define the model stored in the DataBase.
“getGroupAllRbes” returns a Group containing all the RBEs that define the model stored in the DataBase.
“getGroupAllCoordSys” returns a Group containing all the coordinate systems that define the model stored in the DataBase.
“getGroupAllFEM” returns a Group containing all the elements, nodes, rbes and coordinate systems that define the model stored in the DataBase.
This section is devoted to methods that allow the construction of a new Group by selecting entities associated to other entities of the finite element model. For all these methods, the association is checked by inspection of the finite element model stored in the DataBase. Therefore, these methods are defined in the specialized version of the “DataBase” class. Therefore, these methods are systematically defined in specialized versions of the “DataBase” class. For each supported solver, a description of these methods is given. (See Part III.)
As explained in the introduction of this Chapter, the DataBase can be used to store Results. Internally, a mapping between keys and Results allows to associate Result objects to an identifier. Each key1 is characterized by three String objects corresponding respectively to the load case name, to the subcase name and to the Result type name.
The class “Result” is described in Chapter I.4. In this section, one describes the methods of the generic “DataBase” class that deal with “Result” objects. The “Result” methods are:
“getResultLoadCaseNames” is a method without argument that returns an Array containing the names of all the load cases for which Results are stored in the DataBase.
“getResultSubCaseNames” is a method without argument that returns an Array containing the names of all the subcases for which Results are stored in the DataBase.
“getResultTypeNames” is a method without argument that returns an Array containing all the Result identifiers for Results stored in the DataBase.
“checkResultExists” is used to check whether a certain Result is present in the DataBase. The method returns a Boolean value and has three String arguments corresponding to the load case name, the subcase name, and the Result name.
“getResultSize” returns the size of a Result object stored in the DataBase. The method returns an integer value and has three String arguments corresponding to the load case name, the subcase name, and the Result name. If the corresponding Result is not found, “-1” is returned.
“getResultLcInfos” returns the integer and real ids associated to a Result object stored in the DataBase. The method has three String arguments corresponding to the load case name, the subcase name, and the Result name. Integer and real ids are returned in an Array of 4 elements. If specified Result is not found in the DataBase, method returns nil.
“addResult” is used to add a Result to the DataBase. The arguments are three String objects corresponding to the key (load case name, subcase name and Result type name), and the Result object. If a Result with the same key is already present in the DataBase, it is deleted and replaced by the new one.
“generateCoordResults” has three String arguments and builds a Result corresponding to Coordinates of elements and nodes. The arguments correspond to the key to which the Result object is associated in the DataBase. (load case name, subcase name, and Result name respectively.) If the String arguments are omitted, one assumes “”, “” and “Coordinates” for the Result key.
“generateElemAxesResults” has two or three arguments. The two first arguments are the load case name and subcase name to which the produced Results will be associated. These arguments are mandatory. The method produces several vectorial Results:
“Axis 1” corresponding to the first element axis.
“Axis 2” corresponding to the second element axis.
“Axis 3” corresponding to the third element axis.
“Normals” corresponding to the normals to 2D elements.
“Axis” corresponding to the first element axis of 1D elements.
“Coordinates” corresponding to the coordinate Results generated by “generateCoordResults” method.
By default, components are expressed in element axes, except for the “Coordinates” Result which follow the conventions of “generateCoordResults” method. The third argument allows to modify this default behavior by expressing the components in another coordinate system specified by a String or an integer argument. This argument is optional. The use of this option leads to a very significant increase of the computation time of the method.
Note also that the vectorial values are associated to element centers, and element corners. For the “Coordinates” Result, values are also associated to nodes.
“buildLoadCasesCombili” allows the definition of Result by linear combination of other Results. The selection of the new Result and elementary Results is done by load case names. The first argument is a String containing the new load case name of the Results being created. The second argument contains an Array of real numbers corresponding to the factors of the linear combination. The third argument is an Array of Strings containing the name of load cases to which elementary Results are associated. The lengths of the two Array arguments must match.
“renameResults” is used to modify the key by which Results stored in the DataBase can be accessed. The method has two arguments:
An Array of three String objects corresponding to the identification of the Results that must be renamed. If one of the String is void or replaced by nil, then all the Results matching the non void Strings are renamed. Of course, at least one of the three Strings must be non-void.
An Array of three Strings containing the new key identifiers. Strings must be void or nil at the same time as the Strings of “From” argument.
“copyResults” has the same arguments as “renameResults”, and performs nearly the same operation. The difference is that the Result stored in the DataBase is now duplicated, and not simply renamed.
“removeResults” is used to delete Results from the DataBase. This method has two String arguments corresponding to the method of selection of Results and to an identifier respectively. The “Method” argument has three possible values: “CaseId”, “SubCaseId” or “ResId”. It specifies whether the Results to be deleted are identified by their load case name, their subcase name or their Result type name. The second String argument corresponds to the identifier of Results to be deleted.
“removeAllResults” erases all Results stored in the DataBase. This method has no argument.
“getResultCopy” returns a Result object containing a copy of a portion of a Result stored in the DataBase. This method has generally six arguments (see below for other possibilities):
A String argument corresponding to the load case name.
A String argument corresponding to the subcase name.
A String argument corresponding to the Result type name.
A String argument corresponding to the method of selection. Possible values of this argument are listed and explained in Table I.4.6 of section I.4.3. This “Method” string argument can be replaced by a Result or ResKeyList object. Then it correspond to the target entities on which the values are extracted. (See remark below.)
A Group argument corresponding to the Target (selection of elements or nodes on which the Results are recovered).
An Array corresponding to the list of layers on which results are to be recovered. This Array can be void. If not void, its elements must be String or integer objects.
Some of the arguments given above are optional. For example, the function can be called with 3 or 4 arguments only.
When the fourth argument is a Result or a ResKeyList object, the function must have exactly four arguments. Then, it returns a new Result obtained by extracting the pairs of key and values on the keys of the Result or ResKeyList argument.
Valid calls to the function are illustrated below:
res=db.getResultCopy(lcName,scName,resName,"ElemCenters",
targetGrp,layersList)
res=db.getResultCopy(lcName,scName,resName,"NodesOnly")
res=db.getResultCopy(lcName,scName,resName,layersList)
res=db.getResultCopy(lcName,scName,resName)
res=db.getResultCopy(LcName,ScName,ResName,targetRes)
res=db.getResultCopy(LcName,ScName,ResName,targetRkl)
res=db.getResultCopy(lcName,scName,resName,"ElemCenters",
targetGrp)
In the third example above, the extraction is done on the list of layers only, no selection is done for the elements or nodes. In the fourth example, a copy of the Result stored in the DataBase is returned without selection on a list of elements, nodes, layers or sub-layers..
When the method has four arguments, the fourth one is interpreted as a selection method if it is a String. As no extraction Group argument is provided, the extraction is done on all nodes or elements. Also, when four arguments are provided, a single layer cannot be specified as a String argument. It shoud be specified as an Array of Strings. For example:
res=db.getResultCopy(lcName,scName,resName,["Z1"])
is valid, but:
res=db.getResultCopy(lcName,scName,resName,"Z1")
is not.
Methods devoted to the importation of Results from binary Results files are specific to the peculiar solver that produced the Results. These methods are described in Part III.
Four singleton methods allow to enable or disable partially or totally the reading of composite layered Results from finite element result files. These methods influence the behavior of methods defined in the “specialized” versions of the “DataBase” class. (See Part III.) The four methods are:
“enableLayeredResultsReading” enables the reading of layered laminate Results (stresses, strains, failure indices...). This method has no argument. Actually, this method is used to re-enable the reading of layered laminate Results as this reading is enabled by default.
“disableLayeredResultsReading” disables the reading of layered laminate Results (inverse of the previous method). Again, the method has no argument.
“enableSubLayersReading” enables some sub-layers for the reading of composite layered Results from result files. The method has one argument: a String or an Array of Strings chosen among “Bottom”, “Mid” and “Top”. Here again, as by default all the sub-layers are enabled, the method is rather a “re-enabling” method.
“disableSubLayersReading” disables some sub-layers for the reading of composite layered Results from result files. The method has one argument: a String or an Array of Strings chosen among “Bottom”, “Mid” and “Top”.
By default the reading of layered composite Results is enabled for all sub-layers. The disabling may help to reduce the size of Results stored in specialized DataBases. Actually, the reading of composite results is no longer mandatory as most composite results can be produced with the appropriate methods of the “CLA” classes (Part II).
When a Samcef banque is read into a DataBase, the abbreviations defined in the Samcef model are read as well and stored into the Samcef DataBase in a mapping of string objects. Five methods allow the manipulation of abbreviations stored in the DataBase:
“clearAbbreviations” has no argument and clears all the abbreviations stored into the DataBase.
“addAbbreviation” adds one abbreviation to the DataBase. The method has two String arguments: the key and the value.
“addAbbreviations” adds a list of abbreviations to the DataBase. The method has one argument: A Hash object containing the correspondence between keys and values. Each pair is of course a pair of String objects.
“NbrAbbreviations” attribute has no argument and returns the number of abbreviations stored in the DataBase.
“getAbbreviation” returns the String value of one abbreviation. The method has one String argument: the key of the abbreviation.
“checkAbbreviationExists” returns “true” if the abbreviation exists. The method has one String argument: the key of the abbreviation.
“getAbbreviations” returns a Hash object containing all the abbreviations stored in the DataBase. This method has no argument.
Note that, even though no abbreviation is defined in other solver models, the abbreviation methods defined in DataBase class can also be used when one works with all models. This is why the methods listed above are defined in generic “DataBase” class and not in “SamcefDb” class described in Chapter III.2.
The DataBase Class provides one method that returns a ClaDb object corresponding to the materials, plies and Laminates stored in the DataBase. This method is called “getClaDb” and has no argument. The units associated to this ClaDb object are the default units as defined in Table II.1.4. If the finite element model is defined in another unit system, it is the responsibility of the user to define correctly the units of the ClaDb database and of all its entities using the method “setUnitsAllEntities” of ClaDb class. (See section II.2.4.)
Another method corresponding to the calculation of Results related to laminate load response has been added. This method called “calcFiniteElementResponse” has the same arguments as the corresponding method defined in the “ClaLam” class. The method and the meaning of its arguments are described in section II.4.8. The method defined in “DataBase” class differs from the one defined in “ClaLam” class by the fact that the algorithm tries to retrieve the Laminate corresponding to the element to which Result values are attached. The information is found in the DataBase object. More precisely, The algorithm performs as follows:
The property ID or laminate ID corresponding to the element is identified. Then, the algorithm tries to retrieve a laminate with the same ID from the ClaDb argument.
If a laminate object has been identified and extracted, the algorithm performs the same operations has for the method described in section II.4.8.
Otherwise, no Result values are produced for the current key and one tries the next one.
Similarly, one defined the method “calcFiniteElementCriteria” which has exactly the same arguments and outputs as the corresponding method of “ClaLam” class described in section II.4.8. The difference between the two methods resides in the fact that the method in DataBase class retrieves the ClaLam object corresponding to the element to which the tensorial values are attached.
Finally, a third method allows to retrieve laminate engineering properties in the format of Result objects. The method “calcFemLamProperties” has three arguments:
A ClaDb object which is used for the calculations of the different laminate properties.
A ResKeyList object that corresponds to the finite element entities for which values shall be inserted in Result object. Note that the produced Result object are non layered. (Only the ElemId and NodeId of the ResKeyList keys matter.)
A Hash with String keys and values corresponding to the requests. The key corresponds to the name by which the returned Result shall be referred. The value corresponds to the laminate engineering property that is requested. Presently, possible values of this parameter are: “E_f_xx”, “E_f_yy”, “E_k0_xx”, “E_k0_yy”, “E_xx”, “E_yy”, “G_f_xy”, “G_k0_xy”, “G_xy”, “nu_f_xy”, “nu_f_yx”, “nu_k0_xy”, “nu_k0_yx”, “nu_xy”, “nu_yx”, “thickness”, “surfacicMass”, “averageDensity”.
The method returns a Hash with String keys and Result values.
An example of use of this method follows:
...
compDb=db.getClaDb
res=db.getResultCopy("COORD","coord","coordinates")
rkl=res.extractRkl
requests={}
requests["res1"]="thickness"
requests["res2"]="E_xx"
requests["res3"]="E_yy"
resList=db.calcFemLamProperties(compDb,rkl,requests)
resList.each do |id,res|
Util.printRes(STDOUT,id,res)
end
...
For the different “finite element” methods listed above, the units considered for the returned “Result” objects are the units of the “ClaDb” object argument. This characteristic differs from the behavior of the corresponding methods in “ClaLam” class.
One describes here the iterators of the generic DataBase class only. The iterators of the specialized versions of the class are described in Part III.
“each_abbreviation” loops on the abbreviations stored in the DataBase. It produces pairs of Strings corresponding to the name of the abbreviation, and to the corresponding value respectively. Again, one insists on the fact that this iterator is defined in generic DataBase class.
“each_groupName” loops on the Groups stored in the DataBase and produces String elements containing Group names.
The iterator “each_resultKey” produces Arrays containing the keys to which stored Results are associated. This iterator can be used in two different ways. Either:
db.each_resultKey do |lcName,scName,tpName|
...
end
or:
db.each_resultKey do |resKey|
...
end
In the second case, resKey is an Array containing three Strings.
The following methods iterate on the CaseId, SubCaseId and ResultId corresponding to the Results stored in the DataBase:
Each iterator produces String elements.
“each_resultKeyLcScId” iterator produces the pairs of load case names and subcase names for which Results are stored in the DataBase. This iterator can for example be used as follows:
db.each_resultLcScId do |lcName,scName|
...
end
However, if a single argument is passed in the block, it corresponds to an Array of two Strings.
A few more methods with general purpose are defined:
These methods are defined in the generic “DataBase” class.
The “writeGmsh” method defined in generic “DataBase” class is used to create a Gmsh result file in which parts of the model and of the Results are saved for later visualization. The purpose of the method is to allow the user to visualize parts of the model and Results. An example of use of the method is as follows:
db.writeGmsh("brol.gmsh",0,[[res,"stress","ElemCenters"],\
[displ,"displ","Nodes"]],\
[[skelGrp,"mesh slat"]],\
[[skelGrp,"skel slat"]])
The method has six parameters:
A string containing the name of the file in which the model and Results will be output.
An integer corresponding to the id of a coordinate system in which the positions are located and in which the components of Result values are expressed. The coordinate system must be defined in the dataBase db and must be a rectangular one.
An Array containing the Results to be stored in Gmsh file. Each element of the Array is An Array of three elements:
A Result object.
A String corresponding to the name with which the Result shall be referenced in Gmsh.
A String that can have five values: “ElemCenters”, “ElemCorners”, “Elements”, “Nodes”, “ElemCenterPoints” and “ElemNodePoints”. It corresponds to the location of values that are extracted from the Result object to be printed in the Gmsh file. Note:
“ElemCenterPoints” prints the values at center of elements but on a point, no matter the topology of the element. This may be handy for the visualization of Results on zero length elements.
“ElemNodePoints” prints the values at nodes of elements elements on points, no matter the topology of the element.
“Elements” output location combines the outputs at “ElemCorners” and “ElemCenters”. If no value is found at a corner, the algorithm checks whether an output is found at center of element, and uses that value if it is found.
An Array containing the Meshes to be stored in Gmsh file. Each element of the Array is An Array of two elements:
A Group object. The elements contained in the Group will be output in the Gmsh file.
A String corresponding to the name with which the mesh shall be referenced in Gmsh.
An Array containing the parts of the model for which a “skeleton” shall be saved in the Gmsh file. (A skeleton is a representation of the mesh with only a few edges.)
A Group object. The elements contained in the Group will be output in the Gmsh file.
A String corresponding to the name with which the skeleton shall be referenced in Gmsh.
A logical parameter specifying whether a binary output is requested. If the parameter is “true” a binary output is done, otherwise, the output is an ASCII one. The parameter is optional and binary output is the default. A binary output is significantly faster than an ASCII one.
Parameters 3, 4 and 5 are optional. They can be a void Array or replaced by nil argument. All the last nil parameters may be omitted. Parameter 6 is optional too. If no pair of key-values is found for a Result to be printed. Nothing is output in the gmsh file.
It is the responsibility of the user to provide Results that associate values to a single valid key. Otherwise, an error message is issued and exception is thrown. In particular, as Results written in GMSH files are not layered, the user should be careful not to output multi-layered Results. The details in error message output are controlled by the debugging verbosity level. (See I.6.6.)
Note also that if the values that the user try to output are not correct, a substitution is done: Inifinite float values are replaced by MAXFLOAT value, NaN values are replaced by MINFLOAT value. (Of course it is advised to output Result objects with valid values.)
The “writeGmshMesh” method defined in generic “DataBase” class saves a Gmsh mesh file. The method has up to four arguments (last argument is optional):
A String containing the name of the file in which the mesh is output.
An integer argument corresponding to the coordinate system in which the nodes are expressed.
A Group corresponding to the entities to be saved in the mesh file.
An optional Boolean argument specifying whether the mesh is output in binary format. The default value of the argument is “true” and corresponds to a binary output.
An example of use follows:
db.writeGmshMesh("brol.msh",0,skelGrp,false)
It may be practical to manipulate coordinate systems at post-processing level. Therefore, a “CoordSys” class devoted to the manipulation of coordinate systems is proposed. The methods defined in that class are described in sections I.2.2 and I.2.5. A list of the methods defined in “CoordSys” class is given in Table I.2.1.
| Method Name | Description | Example |
| Creation and initialization methods
| ||
| new (s) | I.2.2 | IV.2.4.5 |
| initialize | I.2.5 | |
| clone | I.2.5 | |
| Definition
| ||
| initWith3Points | I.2.2.1 | IV.2.4.5 |
| initWithOV1V2 | I.2.2.2 | |
| initWithOV2V3 | I.2.2.2 | |
| initWithOV3V1 | I.2.2.2 | |
| initWithOV2V1 | I.2.2.2 | |
| initWithOV3V2 | I.2.2.2 | |
| initWithOV1V3 | I.2.2.2 | |
| updateDefWrt0 | I.2.2.2 | |
| Modifying point coordinates
| ||
| changeCoordsA20 | I.2.3.1 | IV.2.4.5 |
| changeCoords02B | I.2.3.2 | IV.2.4.5 |
| changeCoordsA2B | I.2.3.3 | IV.2.4.5 |
Modifying vector or tensor components
| ||
| changeCompsA20 | I.2.4.1 | IV.2.4.5 |
| changeComps02B | I.2.4.2 | IV.2.4.5 |
| changeCompsA2B | I.2.4.3 | IV.2.4.5 |
| Printing
| ||
| to_s | I.2.5 | |
| Attributes
| ||
| Id | I.2.5 | |
A CoordSys object corresponds to a coordinate system. CoordSys objects are generally created in a DataBase when a model is imported.
Besides the data corresponding to the definition of the coordinate system, the CoordSys object also contains a definition of the coordinate system wrt the most basic coordinate system “0”. The corresponding member data are used by functions like the Result methods of modification of reference coordinate systems to perform the transformations of components (sections I.4.6.7 and I.4.6.8). Practically those functions work in two steps:
The components of the Result object are expressed wrt the basic coordinate system “0”.
Then, the components are expressed wrt the new coordinate system.
The definition of the corresponding member data is done by calling the method “updateDefWrt0” (section I.2.2.3).
Besides the “new” class method that returns a new coordinate system initialized to the “0” structural coordinate system, several functions can be used to modify the CoordSys objects.
“initWith3Points” method is used to define a coordinate system with the coordinates of three points A, B and C. (See the definition of “CORD2C”, “CORD2R” and “CORD2S” in [Sof04b].) This function has 5 arguments:
A string argument corresponding to the type of coordinate system being build. Three values are accepted: “CORDC”, “CORDR” and “CORDS”. (Remark that the “2” of Nastran has disappeared.)
A DataBase object that will allow the definition of coordinate system wrt the base coordinate system.
An integer argument corresponding to the reference coordinate system (coordinate system wrt which the coordinates of points A, B and C are given). A coordinate system corresponding to this integer must be defined in the DataBase passed as previous argument.
A vector containing the coordinates of point A. (Point A corresponds to the origin of the coordinate system.)
A vector containing the coordinates of point B. (Point B defines the axis Z of the coordinate system. More precisely, point B is on axis Z.)
A vector containing the coordinates of point C. (Point C defines the axis X of the coordinate system. More precisely, the axis X of the coordinate system is defined in the half-plane defined by the straight-line AB and the point C.)
The three vectors mentioned above are actually Arrays of three real values corresponding to the coordinates of points given in coordinate system identified by the integer argument.
Note that no check is made in a DataBase to ensure that the data are consistent. (For example, checking that the reference coordinate system exists.)
The three methods are “initWithOV1V2”, “initWithOV2V3”, “initWithOV3V1”, “initWithOV2V1”, “initWithOV3V2” and “initWithOV1V3”. They produce CoordSys objects defined by their origin and two direction vectors corresponding to vector and to the orientation of vector respectively.
The six arguments of these methods are:
A string argument corresponding to the type of coordinate system being build. Three values are accepted: ‘CORDC”, “CORDR” and “CORDS”.
A DataBase argument that provides the information needed to complete the definition of the coordinate system.
An integer argument corresponding to the reference coordinate system (coordinate system wrt which the origin and direction vectors are specified).
A vector containing the coordinates of the origin. This origin is specified with an Array of three real values corresponding to the components of O wrt the reference coordinate system identified with the integer argument.
A vector (Array of three real values) corresponding to the direction of the coordinate system. The components of the vector are given wrt to the reference coordinate system (estimated at point if the reference coordinate system is curvilinear).
A vector (Array of three real values) corresponding to the orientation of base vector of the coordinate system. The components of the vector are given wrt to the reference coordinate system (estimated at point if the reference coordinate system is curvilinear).
Note that the orientation vector is not necessarily orthogonal to . If the vectors are not orthogonal, then is a unit vector parallel to , and vector is the unit vector perpendicular to closest to . The last vector of the coordinate system is a unit vector perpendicular to both and .
Here again, no check is made in a DataBase to ensure that the data are consistent. (For example, checking that the reference coordinate system exists.)
“updateDefWrt0” method updates the definition of a CoordSys object wrt to “0” (most basic coordinate system). This function has one argument: the DataBase in which the information needed to build the definition wrt 0 is found.
Note that if one works with several DataBases, the responsibility of managing the correspondence of coordinate systems and DataBases lies on the user.
The “CoordSys” class defines three methods devoted to the transformation of a point coordinates from one coordinate system to another.
Method “changeCoordsA20” is used to calculate the coordinates of a point wrt basic or “0” coordinate system:
The coordinate system on which the method is called is the coordinate system in which the initial coordinates of the point are defined. (Coordinate system “A”.)
The method has one “CoordA” argument: an Array of three real values corresponding to the initial coordinates of the point in coordinate system “A”.
The method returns a “Coord0” Array of three real values corresponding to the coordinate of the same point, but expressed wrt basic coordinate system “0”.
The method is called as follows:
coords0=csA.changeCoordsA20(coordsA)
Method “changeCoords02B” is used to calculate the coordinates of a point wrt a given coordinate system “B”:
The coordinate system on which the method is called is the coordinate system in which one wants to express the point coordinates (Coordinate system “B”.)
The method has one “Coord0” argument: an Array of three real values corresponding to the initial coordinates of the point in basic coordinate system “0”.
The method returns a “CoordB” Array of three real values corresponding to the coordinate of the same point, but expressed wrt coordinate system “B”.
The method is called as follows:
coordsB=csB.changeCoords02B(coords0)
Method “changeCoordsA2B” is used to calculate the coordinates of a point wrt a given coordinate system “B”. The initial coordinate system is a given “A” coordinate system:
The coordinate system on which the method is called is the initial coordinate system in which the point coordinates are expressed (Coordinate system “A”.)
The first “CoordA” argument is an Array of three real values corresponding to the initial coordinates of the point in coordinate system “A”.
The second “CsB” argument is a “CoordSys” object wrt which one wants to calculate the point new coordinates.
The method returns a “CoordB” Array of three real values corresponding to the coordinate of the point expressed wrt coordinate system “B”.
The method is called as follows:
coordsB=csA.changeCoordsA2B(coordsA,csB)
The “CoordSys” class defines three methods devoted to the transformation of a vector or tensor components from one coordinate system to another. These methods are similar to the methods used to transform point coordinates in section I.2.3 but with the following differences:
One modifies the components of a vector or of a tensor.
A vector is defined as an Array of three real values. A tensor is defined as an Array of three Arrays of three real values.
If a vector argument is given, the method returns a vector. If a tensor argument is given, the method returns a tensor.
For each of the methods given here, the coordinates of the point at which the vector or tensor argument is defined, are also given as argument. This means that the methods have one additional argument compared to the corresponding methods of section I.2.3.3. The position of the point matters when curvilinear coordinate systems are involved in the transformation.
Method “changeCompsA20” is used to calculate the components of a vector or tensor wrt basic or “0” coordinate system:
The coordinate system on which the method is called is the coordinate system in which the initial components are defined. (Coordinate system “A”.)
The first “CoordA” argument is an Array of three real values corresponding to the coordinates of the point in coordinate system “A”.
The second “vmA” argument corresponds to the components of vector or tensor (matrix) in coordinate system “A”. (An Array of three real values, or an Array of Arrays of three real values.)
The method returns the components of a vector or tensor, but expressed wrt basic coordinate system “0”. (An Array of three real values, or an Array of Arrays of three real values.)
The method is called as follows:
vm0=csA.changeCompsA20(coordsA,vmA)
Method “changeComps02B” is used to calculate the components of a vector or tensor wrt basic or “B” coordinate system:
The coordinate system on which the method is called is the coordinate system in which one wants to express the components. (Coordinate system “B”.)
The first “Coord0” argument is an Array of three real values corresponding to the coordinates of the point in coordinate system “0”.
The second “vm0” argument corresponds to the components of vector or tensor (matrix) in coordinate system “0”. (An Array of three real values, or an Array of Arrays of three real values.)
The method returns the components of a vector or tensor, but expressed wrt basic coordinate system “B”. (An Array of three real values, or an Array of Arrays of three real values.)
The method is called as follows:
vmB=csB.changeCoords02B(coords0,vm0)
Method “changeCompsA2B” is used to calculate the components of a vector or tensor wrt basic or “B” coordinate system:
The coordinate system on which the method is called is the coordinate system in which the initial components are defined. (Coordinate system “A”.)
The first “CoordA” argument is an Array of three real values corresponding to the coordinates of the point in coordinate system “A”.
The second “vmA” argument corresponds to the components of vector or tensor (matrix) in coordinate system “A”. (An Array of three real values, or an Array of Arrays of three real values.)
The third “CsB” argument is a “CoordSys” object wrt which one wants to calculate the new components.
The method returns the components of a vector or tensor, but expressed wrt basic coordinate system “B”. (An Array of three real values, or an Array of Arrays of three real values.)
The method is called as follows:
vmB=csA.changeCoordsA2B(coordsA,vmA,csB)
One gives here a list of functions that do not fit in any category listed above.
Method “initialize” initializes or clears a CoordSys object. After initializing, the definition corresponds to the “0” structural coordinate system.
“clone” method returns a Copy of the CoordSys object to which it is applied.
“to_s” method is used for printing the Result object.
“Id” integer attribute corresponds to the integer identifier of the CoordSys object. One defines a “setter” and “getter” attribute (“Id=” and “Id” methods respectively).
The “Group” corresponds to the Patran notion of group. Group objects can be stored in a DataBase object, retrieved from it and manipulated outside the DataBase. One describes here the manipulation methods outside the DataBase class.
A list of the methods defined in “Group” class is given in Table I.3.1.
| Method Name | Description | Example |
| Creation and initialization methods
| ||
| new (s) | I.3.2 | IV.2.5.1 |
| initialize | I.3.7 | |
| clone | I.3.7 | |
| Identification (attributes)
| ||
| Name= | I.3.7 | IV.2.2.3 |
| Name | I.3.7 | |
| Manipulation of entities
| ||
| getEntitiesByType | I.3.3 | IV.2.2.2 |
| getNbrEntities | I.3.3 | |
| getNbrEntitiesByType | I.3.3 | IV.2.2.2 |
| setEntities | I.3.3 | IV.2.5.1 |
| setEntitiesByType | I.3.3 | |
| addEntities | I.3.3 | |
| addEntitiesByType | I.3.3 | |
| removeEntities | I.3.3 | |
| removeEntitiesByType | I.3.3 | |
| clearAllEntitiesByType | I.3.3 | |
| matchWithDbEntities | I.3.3 | IV.2.5.1 |
| importEntitiesByType | I.3.3 | |
| containsEntity | I.3.3 | |
| Operators
| ||
| + | I.3.4 | IV.2.5.1 |
| - | I.3.4 | |
| * | I.3.4 | IV.2.2.4 |
| / | I.3.4 | |
| BLOBs for SQL
| ||
| toBlob | I.3.5 | |
| fromBlob | I.3.5 | |
| Iterators
| ||
| each_element | I.3.6 | |
| each_rbe | I.3.6 | |
| each_node | I.3.6 | IV.2.2.2 |
| each_coordsys | I.3.6 | |
| Other methods
| ||
| to_s | I.3.7 | |
| Attribute readers
| ||
| NbrElements | I.3.7 | |
| NbrNodes | I.3.7 | |
| NbrRbes | I.3.7 | |
| NbrCoordsys | I.3.7 | |
A Group is characterized by its name (a String object) and the entities it contains. Four type of entities can be contained in a FeResPost Group: coordinate systems, nodes, elements and rigid body elements (RBEs). At C++ level, for each type of entity, the class group manages a set of integers corresponding to the identifiers of the entities.
Part of the operations dealing with Groups are done by methods defined in DataBase class. The methods of DataBase specially devoted to operations mainly related to Groups are described in section I.1.2.
The singleton method “new” is used to create Group objects.
The class “Group” provides a large choice of methods devoted to the manipulation of the list of entities in its storage. One makes the distinction between operations that modify the content of a Group, and the operations that allow the inspection of this content.
The modification of the Group’s content can be done by calls to the following methods:
“setEntities” takes a String argument that contains the definition of Group entities in a format similar to the format of the Patran Group session file (section I.1.2.1). All entities previously stored in the Group are erased before the conversion of the String argument. The function returns “self” (the modified Group object). As the String argument follows Patran conventions, the list of RBEs follows “MPC” keyword.
“setEntitiesByType” has two arguments. The first argument, “TypeName” is a String object that specifies the type of entities to be added to the Group. This first argument may have four different values: “Node”, “Element”, “MPC” (for rigid body elements) or “CoordSys”. Any other argument is invalid. The second argument may have two different types:
The second argument may be a String object containing the definition of a group in a format similar to the format of the Patran Group session file (section I.1.2.1). However, in this case, only the entities of the type selected by the “TypeName” argument are stored in the Group.
The second argument may also be an Array of integers. Then the integers correspond to the entities added to the Group. The type of entities is specified by the “TypeName” argument.
As for the “setEntities” method, all entities previously stored in the Group are erased before inserting the new entities.
“addEntities” is identical to “setEntities” but the entities stored in the Group are not erased before adding the new entities. As the String argument follows Patran conventions, the list of RBEs follows “MPC” keyword.
“addEntitiesByType” is identical to “setEntitiesByType” but the entities stored in the Group are not erased before adding the new entities.
“removeEntities” is identical to “addEntities” but the selected entities are removed from the Group instead of being added to it. As the String argument follows Patran conventions, the list of RBEs follows “MPC” keyword.
“removeEntitiesByType” is identical to “addEntitiesByType” but the selected entities are removed from the Group instead of being added to it.
“clearAllEntitiesByType” has one String argument corresponding to the type of entities to be cleared from the Group. Possible arguments are “Node”, “Element”, “MPC” (for rigid body elements) or “CoordSys”.
“importEntitiesByType” is used to insert entities in a Group by importing them from another Group, or from the entities stored in a DataBase model. The method has two or four arguments:
The first argument is a String corresponding to the type of entities to be inserted. Possible arguments are “Node”, “Element”, “MPC” (for rigid body elements) or “CoordSys”.
The Second argument is either a Group, or a DataBase.
the third and four arguments are integers corresponding to the range of insertion (idMin and idMax). If omitted, then all entities of the corresponding type are inserted.
“matchWithDbEntities” is used to ensure that a Group contains only entities that are defined in a DataBase. The function has one DataBase argument. After calling this method, the entities that do not exist in the DataBase have been cancelled from the Group too.
Presently, four methods devoted to the manipulation of entities and not modifying the Group have been defined:
“getEntitiesByType” receives one String argument corresponding to the type of entity and returns an Array of integers containing the corresponding entity indices. The four possible values of the argument are “Node”, “Element”, “MPC” (for rigid body elements) and “CoordSys”.
“getNbrEntitiesByType” receives one String argument corresponding to the type of entity and returns an integer corresponding to the number of entities of the specified type contained in the Group. The four possible values of the argument are “Node”, “Element”, “MPC” (for rigid body elements) and “CoordSys”.
“getNbrEntities” has no argument and returns an Array of four integer corresponding to the number of entities of each of the following types, and in the same order as: “CoordSys”, “Element”, “Node” and “MPC” (for rigid body elements).
“containsEntity” allows to check whether a given entity belongs to the Group. The method has two arguments:
The first argument is a String corresponding to the type of entities to be inserted. Possible arguments are “Node”, “Element”, “MPC” (for rigid body elements) or “CoordSys”.
The second integer argument is the entityId.
The function returns a bool value.
A FeResPost Group cannot contain Nastran MPCs.
Eight such operators have been defined. One first explains the meaning and behavior of the four elementary dyadic operations.
“/” operator: if and are two Groups, then . (The operation is equivalent to a logical “exclusive or” operation on the entities.)
Group objects can be saved in SQL database as “BLOB” objects.
Two methods are defined in Group class to convert object to and from Blobs:
“toBlob” has no argument and returns the BLOB in a String object.
“fromBlob” has one String argument corresponding to the BLOB, and initializes the Group according to Blob content.
The class “Group” provides four iterators:
These iterators iterate on the corresponding entities stored in the Group object. They produce Integer values that are passed to the block.
One gives here a list of methods that do not fit in any category listed above:
Method “clone’ returns a Copy of the Group object to which it is applied.
Attribute “Name” returns a String containing the name of the Group.
Attribute “Name=” has one String argument and sets the name of the Group.
Attribute “NbrElements” returns an integer containing the number of elements stored in the Group.
Attribute “NbrNodes” returns an integer containing the number of nodes stored in the Group.
Attribute “NbrRbes” returns an integer containing the number of RBEs stored in the Group.
Attribute “NbrCoordsys” returns an integer containing the number of coordinate systems stored in the Group.
The “Name” and “Name=” methods correspond to the “Name” attribute.
The “Result” class is devoted to the manipulation of finite element Results. Examples of Results are stress tensor on volumic or surfacic elements, displacements, grid point forces,... The ruby class “Result” is a wrapping around the C++ class “Result”.
Results can be read from various solver binary files. See Part III for more information.
The “Result” class allows the storage and manipulation of Real as well as Complex values. Note however that several of the methods of Result class do not allow the manipulation of Complex Results. Therefore, indications are inserted here and there in this Chapter to provide information about the “Complex capabilities” of the different methods.
An important comment must be done: Even though the results can be imported into a DataBase, this does not mean that the manipulation of the results is correct. Indeed, all manipulation that involve transformation of coordinate systems can be incorrect because geometric non-linearities are not taken into account. Methods that can be affected by this limitation are for example: “modifyRefCoordSys”, “modifyPositionRefCoordSys” and “calcResultingFM”.
A list of the methods defined in “Result” class is given in Table I.4.1.
Basically, a Result may be considered as a mapping between “keys” and “values”. These two concepts are discussed in sections I.4.1.1 and I.4.1.2 respectively.
Otherwise several member data of Result objects can be accessed at ruby level. This is the case for Result name, integer and real identifiers. Those are discussed in section I.4.1.3.
The “keys” of Results correspond to the entities to which “values” are associated. For example, a key may be:
The index of an element.
The index of a node.
A pair of integers corresponding to the indices of an element and of a node (for Results given at corners of elements).
A pair of integers corresponding to the indices of an element and of a layer (for example, for layered Results corresponding to laminated properties).
...
So, at C++ level, each key is characterized by four integers:
A 32bits integer corresponding to the element index,
A 32bits integer corresponding to the node index,
A 32bits integer corresponding to the layer index,
An 8bits char corresponding to the sub-layer index (rarely used).
At ruby level, one can work with either the C++ integer ids, or their string correspondent. The correspondence between string and integers are given in Tables I.4.2, I.4.3, I.4.4 and I.4.5. The data given in these Tables can be completed by additional data peculiar to the different supported solvers. (See Part III for more information.)
In Table I.4.4, the last layers IDs cannot be attributed to Result keys. The elements corresponds to groups of layers and are used to perform extraction operations:
“Beam Points” is used to extract on layers “Point A”, “Point B”,...
“Shell Layers” is used to extract on layers “NONE”, “Z1” and “Z2”.
“All Plies ” is used to extract on all layers with positive Ids (i.e. laminate plies).
“All Layers ” extracts on all layers.
| No element association | |
| "NONE" | -1 |
For Results associated to elements | |
| "elem 1" | 1 |
| "elem 2" | 2 |
| "elem 3" | 3 |
| "elem ..." | ... |
| No node association | |
| "NONE" | -999 |
For Results associated to nodes | |
| "node 1" | 1 |
| "node 2" | 2 |
| "node 3" | 3 |
| "node ..." | ... |
| For unlayered Results
| |
| NONE | -999 |
| Undefined layer
| |
| UNDEF | -300 |
| For stress recovery in bars and beams
| |
| "Point A" | -201 |
| "Point B" | -202 |
| "Point C" | -203 |
| "Point D" | -204 |
| "Point E" | -205 |
| "Point F" | -206 |
| For 2D elements | |
| "Z0"1 | -100 |
| "Z1" | -101 |
| "Z2" | -102 |
| For Results in laminates (positive layers)
| |
| "layer 1" | 1 |
| "layer 2" | 2 |
| "layer 3" | 3 |
| "layer ..." | ... |
| Group of layers for extraction operations
| |
| "Beam Points" | -2001 |
| "Shell Layers" | -2002 |
| "All Plies" | -2003 |
| "All Layers" | -2004 |
| "NONE" | 0 |
| "All Sub-Layers" | 50 |
| "Bottom" | 101 |
| "Mid" | 102 |
| "Top" | 103 |
Note that the notion of “key” is also closely related to the “ResKeyList” ruby class which is simply a list of key objects (see Chapter I.5).
The values of Result are characterized by an integer value (32 bits integer) and one or several real values. The integer value corresponds to the coordinate system into which the components are expressed:
-9999 means that the results are not attached to a coordinate system. Their value corresponds to String “NONE”.
-2000 means that the values are expressed in a user defined coordinate system. This means a coordinate system which is not identified by an integer to be later retrieved from a DataBase. The corresponding String is “userCS”.
-1000 means that the values are expressed in a coordinate system projected on surfacic elements. This means also that the values are no longer attached to a peculiar coordinate system defined in a DataBase. The corresponding String is “projCS”.
-6 means the laminate coordinate system. The corresponding String is “lamCS”.
-5 means the patran element IJK coordinate system which correspond to the element coordinate system for most finite element software. The corresponding String is “elemIJK”.
-4 means the ply coordinate system when the element has laminated properties. The corresponding String is “plyCS”.
-3 means the material coordinate system. The corresponding String is “matCS”.
-2 means the nodal analysis coordinate system. Values must then be attached to a node (nodeId of key). The corresponding String is “nodeCS”.
-1 means the element coordinate system. The corresponding String is “elemCS”.
Any integer greater than or equal to zero: a coordinate system defined in a DataBase object. “0” denotes the base Cartesian coordinate system.
Obviously, for several types of coordinate system, the values must be attached to an element to make sense. This is the case for “elemIJK”, “plyCS”, “matCS”, “elemCS”,...
The real values correspond to the components:
A “vectorial” Result (res.TensorOrder=1) has three components named “X”, “Y” and “Z” respectively.
A “tensorial” Result (res.TensorOrder=2) has normally nine components. However, as all the tensors with which one deals are symmetric, only six components are stored: “XX”, “YY”, “ZZ”, “XY”, “YZ”, “ZX”.
A “FieldCS” Result (res.TensorOrder=-10) has nine components. The Result components corresponds to the components of the three direction vectors associated to each key and are given in the followinf order: “1X”, “1Y”, “1Z”, “2X”, “2Y”, “2Z”, “3X”, “3Y”, “3Z” if the three direction vectors are V1, V2 and V3. (See section I.4.1.5.)
Note that the name of the components given above matter, as they may be used to extract a single component out of a vectorial or tensorial Result. For Complex Result, the numbers of components mentioned above is multiplied by two. They are presented in the following order:
First all the Real or Magnitude components are presented.
Then all the Imaginary or Angular components follow. The angular components are expressed in (Nastran convention).
The components are stored in single precision real values (float coded on 32 bits). This means that there is no advantage at using double precision real values in your programming as far as the manipulation of results is concerned.
Besides the mapping from key to values, the Result objects contain information that allow their identification. The identification information is:
The name of the object (a String). This name can be set or retrieved with methods “Name=” and “Name”. These methods correspond to “Name” attribute.
Two integer identifiers that may contain information like the load case id, the mode number,... These member data can set or retrieved with methods “setIntId” and “getIntId”.
Two real identifiers that may contain information related to the time for a transient calculation, to continuation parameters, eigen-values,... These member data can set or retrieved with methods “setRealId” and “getRealId”.
The methods used to access these member data are described in section I.4.6.1.
A Result object is also characterized by two other integer values:
The tensorial order of the values it stores. This integer may be 0, 1 or 2 corresponding to scalar, vectorial or (order 2) tensorial values. (A Tensorial order of -10 corresponds to the special kind of FieldCS Result. See section I.4.1.5.)
The format of the result. This value may be 1 (Real values), 2 (Complex Result in rectangular format) or 3 (Complex Result in polar format).
Methods used to manipulate these data are described in section I.4.6.1. These two integers are attributes of the class.
“FieldCS” Results is a special kind of Result corresponding to the concept of coordinate system defined element by element, node by node, element corner by element corner, etc. Each key of the Result is associated to a Value of nine components corresponding to the components of three local vectors associated to the key.
When defining the “FieldCS” Result one must be careful:
The TensorOrder associated to the Result object is -10!
Only “real” Format makes sense for this kind of Result.
As explained above the FieldCS Result has 9 components corresponding to the components of the three base vectors associated to each key.
The coordinate system in the values must be zero or positive. No systematic check is done when thev Result is created. (Compliance with this rule depends entirely on the disciplin of FeResPost user.)
In each value, the three vectors corresponding to the nine components must be mutually orthogonal and have unit lengths. Again, FeResPost user is responsible for the compliance with this rule. (No check is done by FeResPost.)
FieldCS Results can be used in a limited number of operations only. Actually, They are meant to be used as coordinate system in modifyRefCoordSys method (section I.4.6.7). Note that the components of a FieldCS Result can also be modified by modifyRefCoordSys method but the new CS ID should be >=0.
Actually, as the function mainly meant to be used in method, better efficiency is generally obtained when values components are expressed wrt CS 0.
“assembleFieldCSFrom3Vectors” method is specific to the construction of “FieldCS” type of Results. This method has three vectorial Result arguments. The key-value pairs of the three Result arguments must match.
When Results are read from a Result output file produced by a solver (Part III), the information found in these Result files are used to produce Results with characteristics that are defined according to FeResPost conventions. These characteristics are related to Result naming conventions, Result tensor type, sign conventions, layer associations...
We consider that Nastran solver as a reference for FeResPost solver’s support. Therefore, the naming conventions and other characteristics defined in section III.1.2 are considered as the reference (default) FeResPost Result’s characteristics.
Note also that the subcase names associated to Nastran Results read from XDB, OP2 or HDF files are also considered the reference for other solvers.
The class “Result” defines several methods allowing the construction of a new Result object, or of a “ResKeyList” object from a previously existing Result by an appropriate selection on the keys. The extraction methods defined in class Result are defined in the following sections.
“extractResultOnEntities” method is used to extract a sub-set of keys and values from an existing Result object. The method returns the newly created Result object. The method has up to four arguments:
The “Method” argument is a String object specifying the algorithm to be used to select the keys and values to be inserted in the new Result object. Possible values of this argument are provided in Table I.4.6.
The “Target” argument is a Group containing the elements and/or nodes used by some of the algorithms described above to select sub-sets of Results.
The “LayersList” argument is an Array containing the list of layers on which the pairs of key and value must be extracted. If the Array is void, then data corresponding to all layers are extracted. If the Array is not void, the elements must be String or integer objects
The “SubLayersList” argument is an Array containing the list of sub-layers on which the pairs of key and value must be extracted. If the Array is void, then data corresponding to all sub-layers are extracted. If the Array is not void, the elements must be String or integer objects
The two last arguments are optional. Note that the “Method” argument described above is the same as the “Method” argument of the DataBase member method “getResultCopy” described in section I.1.3. Please refer to that part of the manual for more information on valid extraction data.
This method works for Real as well as for Complex Results.
| “Elements” | All the values associated to the elements of Group “Target” are inserted in the values of the returned Result object. This means that the new Result contains both values at center of element and at corners. |
| “ElemCenters” | All the values associated to the elements of Group “Target” but not associated to any node are inserted in the values of the returned Result object. This means that the extraction returns only values at center of the elements. |
| “ElemCorners” | All the values associated to the elements of Group “Target” and associated to any node are inserted in the values of the returned Result object. The extraction returns only values at corner of the elements. Note that the list of nodes of the “Target” Group is irrelevant for this extraction operation. |
| “Nodes” | All the values associated to the nodes of Group “Target” are inserted in the values of the returned Result object. |
| “NodesOnly” | All the values associated to the nodes of Group “Target” but associated to no elements are inserted in the values of the returned Result object. |
| “ElemNodes” | All the values associated to the elements of Group “Target” AND to the nodes of the same Group are inserted in the values of the returned Result object. This means that the new Result contains only values at corners of elements. |
| “MPCs” | All the values associated to the MPCs (RBEs) of Group “Target” are inserted in the values of the returned Result object. (This extraction method has been added to deal with Grid Point Forces MPC Forces or Moments Results when the “RIGID=LAGR” option is used.) |
| “MPCNodes” | All the values associated to the MPCs (RBEs) of Group “Target” AND to the nodes of the same Group are inserted in the values of the returned Result object. This means that the new Result contains only values at corners of elements. (This extraction method has been added to deal with Grid Point Forces MPC Forces or Moments Results when the “RIGID=LAGR” option is used.) |
“extractResultOnLayers” method is used to extract a sub-set of keys and values from an existing Result object. The method returns the newly created Result object. The method has one “LayersList” argument: it is an Array containing the list of layers on which the pairs of key and value must be extracted. The elements of the Array argument are integers or String values.
This method works for Real as well as for Complex Results.
extractResultOnSubLayers” method is used to extract a sub-set of keys and values from an existing Result object. The method returns the newly created Result object. The method has one “SubLayersList” argument: it is an Array containing the list of sub-layers on which the pairs of key and value must be extracted. The elements of the Array argument are integers or String values.
This method works for Real as well as for Complex Results.
extractResultOnRkl method returns a Result object build by extraction of the values corresponding to the keys contained in the ResKeyList “Target” argument.
This method works for Real as well as for Complex Results.
“extractResultOnResultKeys” method returns a Result object build by extraction of the values corresponding to the keys contained in the Result “Target” argument. (This method is very similar to “extractResultOnRkl” method, except that the target is given by a Result argument.)
This method works for Real as well as for Complex Results.
“extractResultOnRange” method returns a Result object build by extraction of the values selected by specifying a range. This method can be applied to scalar Result objects only as the range is specified by one or two Real values. The arguments of the method are:
The “Method” String argument specifies the extraction algorithm that is used. Four values are possible:
“below”: extraction of the values below the “LowerBound” Real argument value.
“above”: extraction of the values above the “UpperBound” Real argument value.
“between”: extraction of the values between the “LowerBound” and “UpperBound” Real argument value.
“outside”: extraction of the values not between the “LowerBound” and “UpperBound” Real argument value.
The “LowerBound” argument is a real value specifying the lower bound of the range. For some algorithms, this value may be unused and irrelevant.
The “UpperBound” argument is a real value specifying the upper bound of the range. For some algorithms, this value may be unused and irrelevant.
This method works for Real Results only.
“extractResultForNbrVals” method returns a Result object build by extraction of maximum “NbrVals” values. This method can be applied to scalar Result objects only and has two arguments:
The “Method” String argument specifies the extraction algorithm that is used. Two values are possible:
“smallest” causes the method to keep the smallest values of the Result object.
“largest” causes the method to keep the largest values of the Result object.
“NbrVals” is an integer argument corresponding to the number of values to be kept.
This method works for Real Results only.
“extractResultMin” method returns a Result object build by extraction of the minimum value and corresponding key. This method can be applied to scalar Result objects only.
This method works for Real Results only.
“extractResultMax” method returns a Result object build by extraction of the maximum value and corresponding key. This method can be applied to scalar Result objects only.
This method works for Real Results only.
“extractRklOnRange” method works exactly as method “extractResultOnRange” described in section I.4.3.6 but returns a ResKeyList object instead of a Result object. This means that one returns only a list of keys, but not the associated values.
This method works for Real Results only.
“extractRklForNbrVals” method works exactly as method “extractResultForNbrVals” described in section I.4.3.7 but returns a ResKeyList object instead of a Result object. This means that one returns only a list of keys, but not the associated values.
This method works for Real Results only.
“extractRklMin” method returns a ResKeyList object build by extraction of the key corresponding to the minimum value. This method can be applied to scalar Result objects only.
This method works for Real Results only.
“extractRklMax” method returns a ResKeyList object build by extraction of the key corresponding to the maximum value. This method can be applied to scalar Result objects only.
This method works for Real Results only.
“extractRkl” method returns a ResKeyList object build by extraction of all the keys of the Result object to which the method is applied.
This method works for Real as well as for Complex Results.
“extractGroupOnRange” method works exactly as method “extractResultOnRange” described in section I.4.3.6 but returns a Group object instead of a Result object. The Group contains the element and node entities for which values in the specified range have been found.
This method works for Real Results only.
“extractGroupForNbrVals” method works exactly as method “extractResultForNbrVals” described in section I.4.3.7 but returns a Group object instead of a Result object. The Group contains the element and node entities for which values in the specified range have been found.
This method works for Real Results only.
“extractGroup” method returns a Group object containing the elements and nodes that are referenced in the Result object. This method has no argument.
This method works for Real as well as for Complex Results.
“extractLayers” method returns an Array of String and integers corresponding to the layers that are referenced in the Result object. This method has no argument.
This method works for Real as well as for Complex Results.
“extractSubLayers” method returns an Array of String and integers corresponding to the sub-layers that are referenced in the Result object. This method has no argument.
This method works for Real as well as for Complex Results.
All the methods presented in this section are devoted to the production of new results by performing operations on the values of the Result object to which they are applied. Each method produces Results with as many pairs “key-values” as in the Result object to which it is applied, but the number of components associated to each key may be different than the original number of components. Indeed, the original Result and derived Result have not necessarily a same tensor order.
Most of the methods presented below have only one argument: a Method String object corresponding to the algorithm of derivation. The use of the methods defined below leads sometimes to very heavy notations for simple or very often used operations. Therefore, short-cuts to some methods have been defined in the “Post” module (Chapter I.6).
“deriveScalToScal” method builds a new Result object by performing an operation on all the values of the Result object to which it is applied. Both Result objects correspond to scalar values. The Possible values of the “Method” argument are:
“sin”: returns (angle in radians).
“cos”: returns (angle in radians).
“tan”: returns (angle in radians).
“asin”: returns (angle in radians).
“acos”: returns (angle in radians).
“atan”: returns (angle in radians).
“exp”: returns .
“log”: returns .
“exp10”: return .
“log10”: returns .
“abs”: returns .
“inv”: returns .
“sinh”: returns .
“cosh”: returns .
“tanh”: returns .
“sq”: returns .
“sqrt”: .
“sgn”: +1, 0 or -1 depending on the value of argument (arg>0, arg==0 or arg<0 respectively).
The method works for Real Results as well as Complex Results. However, some of the methods are not available for Complex Results: “asin”, “acos”, “atan” and “sgn” can be used with Real Results only. Note that when used with a Complex Result object, the method returns a Complex Result object. There is however one exception to this rule: the “abs” derivation method returns a Real Result.
“deriveScalPerComponent” method builds a new Result object by performing a scalar operation on all the values of the Result object to which it is applied. The Result object can be scalar, vectorial or tensorial. In case, of vectorial or tensorial Result, the scalar operation is performed component-per-component, regardless of the coordinate system in which the values are expressed. The Possible values of the “Method” argument are the same as for deriveScalToScal method. The method works for Real Results only. (Complex Results are not accepted and an exception is raised.)
“deriveVectorToOneScal” method builds a new Result object by performing an operation on all the values of the Result object to which it is applied. The Result object to which the method is applied must be vectorial. The created Result object is scalar. Possible values of the “Method” String argument are:
“Component X”: returns the first component of the vector.
“Component Y”: returns the second component of the vector.
“Component Z”: returns the third component of the vector.
“abs”: returns .
“sq”: returns .
This method works for Real Results as well as for Complex Results. When applied to a Complex Result object, the method works as follows:
The three “Component” methods produce a Complex scalar Result object.
The method “sq” produces the scalar product of the vector by its conjugate. This is a Real scalar Result.
The method “abs” produces the square root of the “sq” method. This is also a Real scalar Result.
“deriveVectorToVector” method builds a new Result object by performing an operation on all the values of the Result object to which it is applied. The Result object to which the method is applied must be vectorial. The created Result object is vectorial too. Possible values of the “Method” String argument are:
“normalize”: normalizes the vectorial values.
This method works for Real Results as well as for Complex Results.
“deriveVectorToTensor” method builds a new Result object by performing an operation on all the values of the Result object to which it is applied. The Result object to which the method is applied must be vectorial. The created Result object is tensorial too. Possible values of the “Method” String argument are:
“extSquare”: builds a tensor from a vector by calculating the external product of the vector by himself. More precisely:
|
|
This method works for Real Results as well as for Complex Results.
“deriveTensorToOneScal” method builds a new Result object by performing an operation on all the values of the Result object to which it is applied. The Result object to which the method is applied must be tensorial. The created Result object is scalar. Possible values of the “Method” String argument are:
“Component XX”: returns the corresponding component of the tensor.
“Component XY”: returns the corresponding component of the tensor.
“Component XZ”: returns the corresponding component of the tensor.
“Component YX”: returns the corresponding component of the tensor.
“Component YY”: returns the corresponding component of the tensor.
“Component YZ”: returns the corresponding component of the tensor.
“Component ZX”: returns the corresponding component of the tensor.
“Component ZY”: returns the corresponding component of the tensor.
“Component ZZ”: returns the corresponding component of the tensor.
“VonMises”: returns the equivalent Von Mises stress assuming that the tensorial Result is a stress.
“MaxShear”: returns the maximum shear evaluated from the maximum and minimum principal values according to Mohr’s theory.
“MaxPrincipal”: returns the maximum principal value.
“MinPrincipal”: returns the minimum principal value.
“det” or “abs”: returns the determinant of the tensor.
“2DMaxShear”: returns the maximum shear evaluated from the maximum and minimum principal values according to Mohr’s theory, assuming that the tensor is a 2D tensor (all components ).
“2DMaxPrincipal”: returns the maximum principal value assuming that the tensor is a 2D tensor (all components ).
“2DMinPrincipal”: returns the minimum principal value assuming that the tensor is a 2D tensor (all components ).
“VonMises2D”: returns the equivalent Von Mises stress assuming that the tensorial Result is a stress. The calculation is done considering that Szz, Sxz and Syz components are zero. (It is user’s responsibility to make sure that the stress tensor is expressed in a coordinate system such that the call to method makes sense.)
All the methods listed above work for Real Tensorial Results. For Complex Results, only the methods of Component extractions can be used.
“deriveTensorToTwoScals” method returns an Array of two Result objects derived from the tensorial Result object on which the method is applied. The returned Results are scalar. Possible values of the “Method” String argument are:
“Principals2D”: returns the principal values of a tensorial Result assuming that the tensor is a 2D tensor (all components ). The first Result contains minimum principal values, and the second Result contains maximum principal Values.
“PrincipalsMinMax”: returns the minimum and maximum principal values of a tensorial Result. The first Result contains minimum principal values, and the second Result contains maximum principal Values.
This method works for Real Results only.
“deriveTensorToThreeScals” method returns an Array of three Result objects derived from the tensorial Result object on which the method is applied. The returned Results are scalar. Possible values of the “Method” String argument are:
“Principals”: returns the principal values of a tensorial Result sorted by order of increasing values. (First Result contains minimum principal values, second Result corresponds to second principal value, and third Result contains the maximum principal values.)
This method works for Real Results only.
“eigenQR” method returns an Array of six Result objects derived from the tensorial Result object on which the method is applied. The method has no argument and the six Results returned correspond to:
The first eigen-value.
The first eigen-vector.
The second eigen-value.
The second eigen-vector.
The third eigen-value.
The third eigen-vector.
Eigen-values and vectors are sorted by order of increasing eigen-values. This method works for Real Results only.
“deriveByRemapping” method returns a Result object obtained by remapping the values of the Result object to which the method is applied. This method takes three parameters:
“FromTo”: a String object specifying the correspondence between the keys of the old Result object and the keys of the new Result object. Eleven different values of the “FromTo” argument are allowed:
“CentersToElemsAndNodes”: one selects all the values at center of elements (i.e. the key of which has an elemId, but no nodeId), then one produce a new Result object with values associated to the corners and edges of those elements.
“CentersToNodes”: one selects all the values at center of elements (i.e. the key of which has an elemId, but no nodeId), then one produce a new Result object with values associated to the nodes of those elements (i.e. the key of which has no elemId but has a nodeId).
“CentersToCorners”: one selects all the values at center of elements (i.e. the key of which has an elemId, but no nodeId), then one produce a new Result object with values associated to the corners of those elements.
“CentersToCornerNodes”: one selects all the values at center of elements (i.e. the key of which has an elemId, but no nodeId), then one produce a new Result object with values associated to the corner nodes of those elements (i.e. the key of which has no elemId but has a nodeId).
“NodesToCenters”: one selects all the values associated to nodes and produces a new Result in which the values are associated to the centers of the elements touching this node.
“NodesToElemsAndNodes”: one selects all the values associated to nodes and produces a new Result in which the values are associated to the elements touching this node, but one keeps the association to the initial node.
“CornersToCenters”: one selects all the values associated to corners (i.e. the key of which has both an elemId and a nodeId corresponding to a corner of this element), and one builds a Result object with values associated to the center of elements.
“CornersToNodes”: one selects all the values associated to corners (i.e. the key of which has both an elemId and a nodeId that corresponds to an element corner), and one builds a Result object with values associated to the corresponding nodes.
“MergeLayers”: one produces a Result object in which for each pair of Element, Node and SubLayer only one Layer is kept. The layerId of each key of the produced Result object is kept uninitialized (i.e. set to -1).
“MergeLayersKeepId”: one produces a Result object in which for each pair of Element, Node and SubLayer only one Layer is kept. The layerId of each key of the produced Result object is the one of the selected key-value of the original Result. For this option only “min” and “max” selection methods are accepted.
“MergeSubLayers”: one produces a Result object in which for each pair of Element, Node and Layer only one SubLayer is kept. The subLayerId of each key of the produced Result object is kept uninitialized (i.e. set to 0).
“MergeSubLayersKeepId”: one produces a Result object in which for each pair of Element, Node and Layer only one SubLayer is kept. The subLayerId of each key of the produced Result object is the one of the selected key-value of the original Result. For this option only “min” and “max” selection methods are accepted.
“MergeAll” merges all the keys and produces a Result object with a single “key-value” pair. The “sum”, “average”, “min” and “max” selection methods are accepted.
“NodesToCorners”: one selects all the values associated to nodes and produces a new Result in which the values are associated to the elements touching this node and of which the node is a corner, and one keeps the association to the initial node.
“CornersToElemsAndNodes”: one selects the values associated to element corners and produces a new Result in which values are associated to all the nodes defining the element. Values are associated to element ID and node IDs.
“ElemsAndNodesToCenters”: one selects all the values associated to elements and nodes (i.e. the key of which has both an elemId and a nodeId), and one builds a Result object with values associated to the center of elements.
“ElemsAndNodesToNodes”: one selects all the values associated to corners (i.e. the key of which has both an elemId and a nodeId), and one builds a Result object with values associated to the corresponding nodes but not to the elements.
“ElemsAllToCenters”: one selects all the values associated to elements corners and center, and one builds a Result object with values associated to the center of elements.
“CornersToElemsAllNodes”: reinterpolates the result values at element corners to other element nodes (typically edge nodes, or node at element center). The available methods are “average” and “sum”. (See below.) Currently, this method is available for Nastran results only.
The different “fromTo” parameters are summarized in Table I.4.7. Remark that one distinguishes the “CornerNodes” (Result keys associated to elements and nodes at corner of elements) and the “ElemsAndNodes” (Result keys associated to elements and nodes of elements but not necessarily at their corners).
“Method”: a String object used to specify the way values associated to different keys are merged into a single value (if this happens). An example of situation in which the case may occur is for example when one uses the “NodesToCenters” option and that the values of several nodes are merged into the value of a single element. Five values of “Method” argument are allowed:
“average”: each merged value is defined as the average of its different contributions.
“sum”: each merged value is defined as the sum of its different contributions.
“min”: one keeps the smallest value. This option can be used for scalar Results only.
“max”: one keeps the largest value. This option can be used for scalar Results only.
“NONE”: this option is used when one is sure that no merging of several values is possible.
Note that when vectorial or tensorial Results are merged (“sum” or “average” options, their respective coordinate systems must be identical. Otherwise an error message is issued.
“DB”: a DataBase object used by the method to recover the association of node and elements. This association is often needed to perform the remapping.
The “deriveByRemapping” method can be used with Real as well as Complex Results. Only, for Complex Results, there are some restriction about the type of “Method” argument for merging values: the “min” and “max” values are not accepted for Complex Results.
| “fromTo” argument | Source | target | Target key types |
| “CentersToCorners” | Element Centers | Element Corners | EN** |
| “CentersToNodes” | Element Centers | Nodes of Elements | -N** |
| “NodesToCenters” | Nodes | Element Centers | E-** |
| “NodesToCorners” | Nodes | Element corners | EN** |
| “CornersToCenters” | Element Corners | Element Centers | E-** |
| “CornersToNodes” | Element Corners | Nodes of Elements | -N** |
| “MergeLayers” | Layers | - | EN-* |
| “MergeLayersKeepId” | Layers | Layers | EN** |
| “MergeSubLayers” | Sub-layers | - | EN*- |
| “MergeSubLayersKeepId” | Sub-layers | Sub-layers | EN** |
| “MergeAll” | All keys | - | —- |
| “CentersToElemsAndNodes” | Element Centers | Element Nodes | EN** |
| “CornersToElemsAndNodes” | Element Corners | Element Nodes | EN** |
| “CentersToCornerNodes” | Element Centers | Element Corner Nodes | -N** |
| “ElemsAndNodesToCenters” | Element Nodes | Element Centers | -N** |
| “ElemsAndNodesToNodes” | Element Nodes | Nodes | -N** |
| “NodesToElemsAndNodes” | Nodes | Element Nodes | EN** |
Presently, only one such method is defined: the “deriveDyadic” method. This method returns a new Result object corresponding to the dyadic derivation. This method has two arguments:
The “Method” String argument corresponds to the name of the dyadic method that is used for the calculation of new Result’s values.
The ”Second” argument can be a Result object or a real value. The Result object is always a valid argument if its tensor order is compatible of the operation being performed. The “real” argument is valid only if the invoked method is “atan2” or “pow”.
Possible values for the “Method” argument are:
“atan2” performs the “atan2” operation on its argument values (). The object on which the method is called must be a scalar Result object. The “Second” argument must be either a scalar Result or a real value. For a real argument, one calculates
“pow” performs the “pow” operation on its argument (). The object on which the method is called must be a scalar Result object. The “Second” argument must be either a scalar Result or a real value. For a real argument, one calculates for each .
“vectProduct” calculates the vectorial product of its arguments. Several types of arguments are accepted:
The two arguments are vectorial Result objects. Then, .
The second argument can be replaced by a vector (Array of three real elements). Then, one calculates .
The first argument can be replaced by a vector (Array of three real elements) or a complex vector (Array of three complex elements). Then, .
“sumVectProduct” calculates the sum of the vectorial product of its arguments: . The two arguments are vectorial Result objects.
“min” keeps the minimum of the two values. Values must be Real. If the arguments are not scalar, they must have common tensorial order, and for each key-value pair, the coordinate system ID of the arguments must match. Then, the derivation is done component per component.
“max” keeps the maximum of the two values. Values must be Real. If the arguments are not scalar, they must have common tensorial order, and for each key-value pair, the coordinate system ID of the arguments must match. Then, the derivation is done component per component.
“compare” sets the value of new Result to -1, 0 or 1 depending on the relative first and second values. Values must be scalar and Real. If the arguments are not scalar, they must have common tensorial order, and for each key-value pair, the coordinate system ID of the arguments must match. Then, the derivation is done component per component.
“merge” or “mergeKeepFirst” keeps the value of the first Result if a given key is present in the two values. Otherwise the pair key-value of the second Result is kept.
“mergeKeepLast” keeps the value of the second Result if a given key is present in the two values. Otherwise the pair key-value of the first Result is kept.
Note that several of the methods above for dyadic derivation have corresponding short-cuts in the “Post” module.
The different methods listed above are available for real Results. For Complex Results, only the methods “vectProduct”, “sumVectProduct”, “merge”, “mergeKeepFirst” and “mergeKeepLast” can be used. Of course, if the ”Second” argument is a Real object, the “deriveDyadic” method cannot be invoked on a Complex Result object.
Note also that all the dyadic derivation methods discussed here are invoked on a Result object which is the first argument. Dyadic derivation methods that allow to replace the first argument by a real or vector object are also defined in the Post module. (See section I.6.3.)
One presents here methods that modify the Result object to which they are applied.
Each Result object is also characterized by two integer and two real identifiers. Different methods allow to retrieve or modify the Result data.
“Name” returns a String containing the name of the Result. The method has no argument.
“Name=” has one String argument and sets the name of the Result.
“Format” returns an integer corresponding to the format of the Result (1="Real", 2="Real-Imaginary", 3="Magnitude-Phase").
“Format=” has one integer argument and sets the format of the Result object. (Same possible values as for “Format” attribute “getter”.)
“TensorOrder” returns an integer corresponding to the tensorial order of the Result. (Possible values are 0, 1, 2 and -10.)
“TensorOrder=” has one integer argument and sets the tensorial order of the object. (Possible values are 0, 1, 2 and -10.)
“clearData” has no argument and clears the keys and values stored in a Result object. The method returns the modified “Result” object.
“insert” has two Array arguments corresponding to a result::key and a result::values respectively:
The “Key” argument is an Array of between 1 and 4 elements corresponding to element, node and layer identifiers respectively. These elements can be of String or integer types.
The “Values” argument is an Array of elements the number of which depends on the tensorial order of the Result object that is filled. (This tensorial order must have been defined already.) The first element of the Array is always the coordinate system identifier (a String or integer object). The other elements of the Array are Real values corresponding to the components.
The method returns the modified “Result” object.
“insertRklVals” has two arguments corresponding to a ResKeyList or Result object and a result::values object respectively:
The “Rkl” is a ResKeyList or Result object containing the list of keys for which values are inserted. This argument can be replaced by a Result object; then, only the keys of the Result are used for insertion of data.
The “Values” is the same argument as in “insert” method described above. Note that one inserts identical values for the different keys of the “Rkl” ResKeyList object.
The method returns the modified “Result” object.
“insertResultValues” has one “Result” argument. The keys and values of the argument “Result” object are inserted to the Result object on which the method is called. The method returns the modified “Result” object.
“setComponent” has two or three arguments and allows to modify a selected component of the values stored in the Result object on which the method is called:
If the method has three arguments:
The first “oComp” argument is an integer corresponding to the index of the component that shall be modified.
The second “inRes” argument is a Result object from which the new component values are read.
The third “iComp” argument is an integer corresponding to the index of the component that is read from the “inRes” Result object.
The values of the target Result object (on which the method is called) are modified only for the keys that are found in the “inRes” Result argument. It is the responsibility of the user to defined correct “oComp” and “iComp” indices. (First component corresponds to index 0.)
If the method has two arguments:
The first “oComp” argument is an integer corresponding to the index of the component that shall be modified.
The second “fValue” argument is a real value corresponding to the new component value.
With this version of the method, all the values of the target Result object are modified. Here again, the user is responsible for the correct definition of “oComp” argument.
The method returns the modified “Result” object.
“removeKeysAndValues” is used to remove keys and values from an existing “Result” object. If the method has one argument, the arguments is either a “Result” or a “ResKeyList” object. Then, keys and values are removed for all the keys found in the argument. If two arguments are provided, they must be a “method” String argument, and a “Group” argument, and the method keys are eliminated according to the “getData” method. The method returns the modified “Result” object.
“setIntId” has two arguments: the index of integer ID to be set, and its new value.
“getIntId” has one argument: the index of integer ID that is to be retrieved.
“setRealId” has two arguments: the index of real ID to be set, and its new value.
“getRealId” has one argument: the index of real ID that is to be retrieved.
For the four last methods listed above, the value of index argument can be 0 or 1. Note that several of the methods listed above correspond to the “Name”, “Format” and “TensorOrder” attributes.
All these methods can be used with Real Results as well as with Complex Results.
“setRefCoordSys” is used to attribute a reference coordinate system to the values of a Result. The method has one argument that can have to types:
An integer corresponding to the integer ID of the associated coordinate system.
A String corresponding to the names of peculiar coordinate systems. The possible values for the String are “NONE”, “userCS”, “projCS”, “elemCS”, “nodeCS”, “matCS”, “plyCS” and “elemIJK”.
Note that only the coordinate system ids of the pairs of key and values are modified. The components of the vectorial or tensorial values are left unchanged.
This method can be used with Real Results as well as with Complex Results and returns the modified “Result” object.
“renumberLayers” is a method used to renumber the layer integer ids of Result keys. The method has one Hash argument corresponding to the pairs of “old integers IDs” and “new integer IDs”.
This method can be used with Real Results as well as with Complex Results and returns the modified “Result” object.
“renumberSubLayers” is a method used to renumber the sub-layer integer ids of Result keys. The method has one Hash argument corresponding to the pairs of “old integers IDs” and “new integer IDs”.
This method can be used with Real Results as well as with Complex Results and returns the modified “Result” object.
“removeLayers” is a method used to remove pairs of key and values selected on the basis of the layer ID of the key. The method has one “LayersList” argument: it is an Array containing the list of layers for which the pairs of key and value must be removed. The elements of the Array argument are integer or String values.
This method can be used with Real Results as well as with Complex Results and returns the modified “Result” object.
“removeSubLayers” is a method used to remove pairs of key and values selected on the basis of the layer ID of the key. The method has one “SubLayersList” argument: it is an Array containing the list of sub-layers for which the pairs of key and value must be removed. The elements of the Array argument are integer or String values.
This method can be used with Real Results as well as with Complex Results and returns the modified “Result” object.
“modifyRefCoordSys” is used to modify the reference coordinate system wrt which the components of a vectorial or a tensorial Result are applied. If the Result is vectorial it can represent any vectorial quantities except the coordinates. For coordinate vectorial Result, the method “modifyPositionRefCoordSys” must be used. This method has no effect on scalar Results.
The methods returns nil (no new Result object is created) and takes two, three or five arguments:
An object corresponding to the definition of the coordinate system to which one switches. This object may have different types:
A String object with one of the following values: “elemCS”, “nodeCS”, “matCS”, “plyCS”, “elemIJK”, “lamCS”. All those coordinate systems are local to an element or to a node.
More information about the peculiarities of “matCS”, “plyCS” and “lamCS” coordinate system transformations is given in section X.B.5.
The argument may by a CoordSys object. Then it must be defined wrt a coordinate system defined in the DataBase argument.
The argument may by a Results object. This should then be a FieldCS Result. (See I.4.1.5.)
The argument may also be an integer larger than or equal to 0. Then the coordinate system must be defined in the DataBase.
The third argument is the direction vector used to build the projected coordinate system on surfacic elements. The vector is given by an Array of three real objects, and is expressed wrt to the coordinate system given in second argument. If one does not wish to transform into a projected coordinate system, then the third argument must be omitted or nil. (However if arguments 4 and 5 are provided, the third argument cannot be omitted.)
An object corresponding to the definition of the coordinate system from which one switches. This object may have the same values as the second argument.
The last argument is a direction vector used to build the projected coordinate system on surfacic elements. The vector is given by an Array of three real objects, and is expressed wrt to the coordinate system given in second argument. If one does not wish to transform into a projected coordinate system, then the third argument must be nil.
The reason why a DataBase object is given as argument is that for curvilinear coordinate systems, much information about the location of Result value is necessary to perform a correct transformation of the components. Also, all coordinate systems are stored in the DataBase object. Therefore, it is very important that the programmer keeps in mind that all Results are related to a DataBase.
Note that some transformation vectorial or tensorial coordinate systems cannot be reversed. For example, once a Result is expressed in a projected coordinate system. Also, if a conversion has been done in a coordinate system that is not defined in the DataBase, the conversion is impossible. After transformation, the coordinate system referenced in Result values is altered (section I.4.1.2).
If arguments 4 and 5 are provided, the method assumes that the values are expressed in that coordinate system definition. This means that the CsId found in each pair “key-values” pair of the Result object is totally disregarded. The use of arguments 4 and 5 may allow the modification of Results expressed in a user or projected coordinate system.
More information on the transformation of coordinate systems is given in section X.B.4.
This method can be used with Real Results as well as with Complex Results and returns the modified “Result” object.
“modifyPositionRefCoordSys” method is used to modify the reference coordinate system wrt which vectorial Results corresponding to coordinates are expressed. The Results must be vectorial.
The method returns nil (no new Result object is created) and takes two arguments:
An integer object corresponding to the index of the coordinate system to which one switches. This index must be larger than or equal to 0 and defined in the DataBase argument. One can also provide a CoordSys object instead of the integer argument.
For the reason of the presence of the DataBase argument, see section I.4.6.7.
This method can be used with real Results only and returns the modified “Result” object.
“setToCombili” method fills the values of the Result object on which the method is called with the linear combination of the elementary Results given as arguments. The arguments are defined as follows:
An Array of Real values containing the factors of the linear combination.
An Array containing the elementary Results.
The lengths of the two Array arguments must match. Also the type of elementary Results (scalar, vectorial or tensorial) must be identical and the coordinate systems must be the same for a same key.
This method can be used with Real Results as well as with Complex Results. Also, the real factors of the linear combination can be replaced by Complex values. However, all the elements of the Array must be of the same type (Real or Complex).
The “setToCombili” method returns the modified “Result” object.
“setToCombiliPerComponent” method fills the values of the Result object on which the method is called with the linear combination of the elementary Results given as arguments. The difference with “setToCombili” method is that the factors of the linear combination are given component-per-component. Practically, the “factors” argument is a 2D Array (Array of Arrays):
The first index corresponds to the lines of the “factors” Array, and one has as many lines as one has results in the linear combination.
The second index corresponds to the columns of the “factors” Array, and one has as many columns as results have components.
Five elementary operators on Result objects have been defined. Also, their corresponding assignment method have been defined. Unless otherwise specified, in the examples given below, , and are Result objects. One of the two operands can be replaced by a “constant” value in most cases, but at least one of the operands must be a Result object:
By “constant” value, one means a scalar real value, a scalar complex value, a real vector (Array of three real values), a complex vector (Array of three complex elements), or a real matrix (Array of real values). These arguments can be used in addition, substraction and multiplication operations. Note that no constant complex matrix is supported.
For the division operation, can be replaced by a scalar real or complex argument, but not by a vector or a matrix. on the other hand, can be replaced by constant scalar, vectorial or matrix, real or complex (except for the matrix).
For the exponentiation operator, the two Results must be scalar. Either or can be replaced by a constant real value.
One can make a few general remarks:
When the two arguments are vectorial or tensorial Results, the coordinate system ids must be the same for each corresponding values.
The coordinate system associated to the values of the constructed Result is defined according the following rules:
For a scalar Result , the cId is always set to -9999 (Result not associated to a coordinate system).
For a vectorial or tensorial Result, the coordinate system for each value is set to the corresponding coordinate systems of the vectorial or tensorial arguments.
When it is not possible to determine the Result coordinate system according to the preceding rules, the CID is set to 0 for all values. An example of such a case is the division of an Array by a scalar Result.
The operators are defined in the Result class. This means that the first operand must be a Result object. However, to the different operators defined in Result class corresponding “operator” methods defined the “Post” module. Several of the “Post” methods allows to replace the first operand by a real object or an Array. (See section I.6.4.)
Note that this rule does not apply to the .NET assembly that allows the first operand of the different operators to be replaced by constant values.
The support for Complex Result operators depends on the type of dyadic operation. See the sub-sections below for more information.
The addition operator can be used as follows:
|
|
In the previous expression, the Results and must have the same tensorial order. Of course, the returned object is also of the same tensor order as and .
The substraction operator can be used as follows:
|
|
In the previous expression, the Results and must have the same tensorial order. Of course, the returned object is also of the same tensor order as and .
The multiplication operator can be used as follows:
|
|
The meaning of this operation depends on the tensorial orders of and . The various possibilities are summarized in Table I.4.8 with a short explanation of the meaning of the operation when deemed necessary.
| meaning | |||
| S | S | S | — |
| V | S | V | — |
| M | S | M | — |
| V | V | S | — |
| S | V | V | scalar product of two vectors |
| V | V | M | left multiplication of a matrix by a vector |
| M | M | S | — |
| V | M | V | right multiplication of a matrix by a vector |
The division operator can be used as follows:
|
|
In the last expression can have any tensorial order. The tensorial order of the returned Result is identical to the tensorial order of . The argument can be either a scalar Result object, or a real value.
Complex Results are partially supported by the division operator. The limitations of the operator for complex arguments are the same as for the multiplication operator.
The exponentiation operator can be used as follows:
|
|
In the last expression must be a scalar Result. The tensorial order of the returned Result is identical to the tensorial order of . The argument can be either a scalar Result object, or a real value. Complex Results cannot be arguments to this operator. The real values of first Result argument must also be positive.
The three following expressions are equivalent:
z=x**y z=Post.pow(x,y) z=Post.opPow(x,y)
“calcResultingFM” method is a class method used to estimate the total force and moment corresponding to a distribution of forces and moments on several points. The method has between 4 and 6 arguments:
A DataBase object containing the model used to calculate the total forces and moments.
A first Result object corresponding to the vectorial forces.
A second Result object corresponding to the vectorial moments.
An object corresponding to the coordinate system in which results and position of recovery point are expressed. If the argument is an integer, it must correspond to the index of a CoordSys object defined in the dataBase. The argument can also be a CoordSys object, but its definition must refer a coordinate system defined in the dataBase.
A vector (Array of three real values) corresponding to the position of the point wrt which the total force and moment are calculated. The position of the point is defined wrt the coordinate system corresponding to the previous argument. (This may different than what other post-processing tools like Patran do.)
A Result object corresponding to the coordinates of the connections that are used to estimate the global moment. (See additional remarks below.)
Note that the two last arguments are optional:
If argument 5 is omitted, the method assumes that the recovery point is located on the origin of the coordinate system.
I argument 6 is omitted, the nodal coordinates are used to estimate the global moment corresponding to the nodal forces (). Then, the forces used to estimate the global moment must be associated to nodes.
The sixth parameter containing the coordinates must be associated to the same Result keys as the forces Result. The parameter can be very useful when the forces are not associated to nodes. This is, for example, the case when the forces correspond to CBUSH element forces. For example, let us assume that the coordinate Results have been generated in the database:
db.generateCoordResults("COORDS","COORDS","coords")
The coordinates corresponding to the forces can be obtained as follows:
coords=db.getResultCopy("COORDS","COORDS","coords",forces.extractRkl())
And the global force and moment calculated as follows:
fm=Result::calcResultingFM(db,forces,moments,csId,nil,Coords)
If argument Results are in Real format, the method returns an Array containing two vectors (i.e. two Arrays of Real objects). These vectors correspond to the total force and total moment respectively. Note that the method produces no new Result object.
If argument Results are Complex, the method returns an Array containing two Complex vectors (i.e. two Arrays of Complex objects). Note However that the Complex values in the resultants are always given in rectangular format (real and imaginary parts). This is true even when the argument Results are in polar (magnitude-phase) format.
Several methods correspond to operations specific to complex Results. These methods are described below.
Two methods allow to tranform Complex Results expressed in real-imaginary format to magnitude-phase format, and reversely:
“set2RI” produces a complex Result in rectangular (real-imaginary) format. The method has 0 or 1 argument. If the method has one argument, the object on which the method is called is set to the rectangular complex values of its argument. Otherwise, the object on which the methods is called is modified.
“set2MP” produces a Complex Result in polar (magnitude-phase) format. The method has the same characteristics as “set2RI”.
For these two methods, no complex conversion is performed if the Result is already in the requested format.
“conjugate” produces a Result by initializing its values to conjugate of other values (). The method has 0 or 1 argument. If the method has one argument, the object on which the method is called is set to the rectangular complex values of its argument. Otherwise, the object on which the methods is called is modified. Note that the method can also be called on a Real Result but has then no effect.
The method “rotateBy” is used to modify the values of a Complex Result by adding an angle specified in degrees to the corresponding phases. However, the method can be used indifferently with Complex Results in rectangular or in polar formats. The method may have one or two arguments:
If the method has only one argument, it is the angle that is added to the phase. The modified argument is the Result object on which the method is called.
If the method has two arguments, the first one is a Result object, and the second one is the rotation angle in degrees. Then the Result object on which the method is applied is initialized to the rotated argument Result object.
Note that the rotation is done by multiplying the Result by a Complex value obtained as follows:
|
|
Angle is always given in .
Four methods produce Real Results from Complex Results by extracting the appropriate components:
These methods must be called on Complex Results. The polar or rectangular format of the Complex Results does not matter: if needed a polar-rectangular conversion of the components is done before the extraction.
The two methods “getR” and “getI” may have an optional Real argument that corresponds to a rotation applied to the Result before extracting the Real or Imaginary component Result. More precisely, each component of each value is multiplied by before extracting the real or imaginary component. Angle is always given in . Note that the Result on which the method is called is left unmodified.
The “assembleComplex” method is used to assemble a Complex Result object from two Real Results. The method is called on a Result object and has three arguments:
An integer corresponding to the format of the new Complex Result. The accepted values are 2 (real-imaginary or rectangular format) or 3 (polar or magnitude-phase format).
A first Result object that will correspond to the real or magnitude components of the assembled Result.
A second Result object that will correspond to the imaginary of phase components of the assembled Result.
Note that the two Result arguments must satisfy several requirements:
They must be Real Results.
They must have the same number of key-values pairs, with exact key matches.
Their values must have the same number of components.
When one pair of value objects are merged, their Coordinate System IDs must be the same.
An example of valid (but not very useful) call to “assembleComplex” follows:
resR=res2.getR resI=res2.getI resRI=Result.new resRI.assembleComplex(2,resR,resI)
(At the end, resRI should be the same as res2.)
The getData method returns an Array of Arrays containing the data stored in a Result object. The returned Array may actually be considered as a two-dimensional Array with as many lines as there are pairs of key-value in the Result object. Each line of the Array contains 6, 8 or 11 elements:
The first element corresponds to the elemId.
The second element corresponds to the nodeId of the key.
The third element corresponds to the layerId of the key.
The fourth element corresponds to the subLayerId of the key.
The fifth element corresponds to the coordinate system in which the value components are associated. The possible values are summarized in Table I.4.9.
The other elements are real values corresponding to the components (1, 3 or 6 values for a scalar, vectorial or tensorial Result respectively). For the precise meaning of the returned value corresponding to coordinate system, see also section I.4.1.2.
The method may have 5, 4, 3, 2, 1 or no argument. The arguments correspond to the type of the Array elements corresponding to elemId, nodeId, layerId, subLayerId or coordSysId. In the returned Array, these elements may be of String or Integer types. Correspondingly the arguments are Strings the value of which can be "int", "string" or any other String. If any other String is used as argument (for example a void string), the default Integer or String type elements are returned.
For element, node and layer ids, the negative values correspond to “special” values. (See Tables I.4.2 to I.4.4.)
| integer in C++ “value” class | returned value in ruby |
| -9999 | nil |
| -2000 | "userCS" |
| -1000 | "projCS" |
| -5 | "elemIJK" |
| -4 | "plyCS" |
| -3 | "matCS" |
| -2 | "nodeCS" |
| -1 | "elemCS" |
| any other integer | the same integer |
Result objects can be saved in SQL database as “BLOB” objects.
Two methods are defined in Result class to convert object to and from Blobs:
“toBlob” has no argument and returns the BLOB in a String object.
“fromBlob” has one String argument corresponding to the BLOB, and initializes the Result according to Blob content.
Three iterators are defined in the class:
“each” iterates on the data and produces pairs of key and values. Each key is an Array of four elements, and each “values” and Array of 2 to 7 elements. The iterator may have between 0 and 5 arguments. The arguments are Strings that specify whether some of the data are to be returned in String or integer format. The consecutive arguments correspond to the formatting of element id, node id, layer id, sub-layer id and coordinate system id.
“each_key” iterates on the data and produces Arrays of three elements corresponding to keys. The iterator may have between 0 and 4 argument. The arguments are Strings that specify whether some of the data are to be returned in String or integer format.
“each_values” iterates on the data and produces Arrays of 2 to 7 elements. The iterator may have 1 or no String argument specifying the Type of the element corresponding to the coordinate system identifier.
For the meaning of the arguments, see more information in section I.4.10. One difference between the “each” iterator and the getData method is that the key and values elements are separated into two Arrays in the block. So the iterator is to be used as follows:
strain.each("int","int","int") do |key,values|
...
end
...
strain.each("int","int","string","string") do |key,values|
...
end
Note that, as the “each_key” and “each_values” iterators return Arrays, one can indifferently recover an Array argument, or its elements in the arguments of the block that follows the iterator. For example, in the following lines:
stress.each_key do |stressKey| ... end
“stressKey” is an Array of three elements. However in the following lines:
stress.each_key("int","int","int") do |elemId,nodeId,layerId|
...
end
the arguments correspond to the different identifiers of the Result key.
Four singleton methods allow to convert layers and sub-layers string/integer IDs:
“layerStr2Int” converts a layer name to its corresponding layer integer ID.
“layerInt2Str” converts a layer integer ID to the corresponding name (String).
“subLayerStr2Int” converts a sub-layer name to its corresponding layer integer ID.
“subLayerInt2Str” converts a sub-layer integer ID to the corresponding name (String).
One gives here a list of methods that do not fit in any category listed above.
“new” method is used to create a new Result object.
“initialize” method initializes or clears a Result object.
“clone” method returns a Copy of the Result object to which it is applied.
“cloneNoValues” method returns a Copy of the Result object to which it is applied, except that no values are inserted. Practically, it means that one copies attributes like the name, the tensor order, the format...
“initZeroResult” method is used to initialize a Result with zero values using the keys of an existing Result object. The Method has four arguments:
A String corresponding to the Name of the Result.
An integer corresponding to the tensor order (0, 1 or 2).
An integer corresponding to the Format of the Result.
A Result object that provides the keys to which the zero values of the new Result object will be associated.
The method returns the Result object on which it has been called.
“Size” returns an integer containing the numbers of pairs “key-value” contained in the Results object. This method has no argument. It corresponds to the “Size” read-only attribute.
“to_s” method is used for printing the Result object.
A ResKeyList object is basically a set of Result keys (see Chapter I.4). Actually, a ResKeyList object is a kind of Result with no values associated to the keys.
One shows in section I.4.3 that several methods of class Result allow to build ResKeyList objects from Results, and to extract Results from other Results using ResKeyList objects.
A list of the methods defined in “ResKeyList” class is given in Table I.5.1.
| Method Name | Description | Example |
| Creation and initialization
| ||
| new (s) | I.5.1 | IV.2.5.1 |
| initialize | I.5.1 | |
| clone | I.5.1 | |
| insert | I.5.1 | |
| getData | I.5.6 | |
| Size | I.5.7 | |
| Identification
| ||
| Name= | I.5.7 | |
| Name | I.5.7 | |
| Extractions
| ||
| extractLayers | I.5.2 | |
| extractSubLayers | I.5.2 | |
| extractGroup | I.5.2 | |
| Layers and sub-layers manipulation
| ||
| renumberLayers | I.5.3.1 | |
| renumberSubLayers | I.5.3.2 | |
| removeLayers | I.5.3.3 | |
| removeSubLayers | I.5.3.4 | |
| Operators
| ||
| + | I.5.4 | |
| - | I.5.4 | |
| * | I.5.4 | |
| / | I.5.4 | |
| Iterators
| ||
| each_key | I.5.5 | |
| Printing
| ||
| to_s | I.5.7 | |
| Attributes
| ||
| Name | I.5.7 | |
| Size | I.5.7 | (read only) |
The usual “new” and “initialize” singleton methods are defined in the ResKeyList class. These methods have no arguments. The class member method “clone” has no argument and returns a copy of the object.
The user can fill its one ResKeyList object with the “insert” method. This method takes one Array Argument with between 1 and 4 elements corresponding to the element identifier, the node identifier, the layer identifier and the sub-layer identifier. Each element can be a String or an integer.
Two extraction functions have been defined:
“extractLayers” returns an Array of String and integers corresponding to the layers that are referenced in the ResKeyList object.
“extractSubLayers” returns an Array of String and integers corresponding to the sub-layers that are referenced in the ResKeyList object.
“extractGroup” returns a Group object containing the elements and nodes that are referenced in the ResKeyList object.
These methods have no arguments.
The two methods described below correspond with the methods with identical names defined in “Result” class.
“renumberLayers” is a method used to renumber the layer integer ids of ResKeyList keys. The method has one Hash argument corresponding to the pairs of “old integers IDs” and “new integer IDs”.
“renumberSubLayers” is a method used to renumber the sub-layer integer ids of ResKeyList keys. The method has one Hash argument corresponding to the pairs of “old integers IDs” and “new integer IDs”.
“removeLayers” is a method used to remove keys selected on the basis of the layer ID of the key. The method has one “LayersList” argument: it is an Array containing the list of layers for which the keys must be removed. The elements of the Array argument are integer or String values.
“removeSubLayers” is a method used to remove keys selected on the basis of the layer ID of the key. The method has one “SubLayersList” argument: it is an Array containing the list of sub-layers for which the keys must be removed. The elements of the Array argument are integer or String values.
Eight such operators have been defined. One first explains the meaning and behavior of the four elementary dyadic operations.
“/” operator: if and are two ResKeyLists, then . (The operation is equivalent to a logical “exclusive or” operation on the entities.)
One “each_key” iterator is defined in the class: it iterates on the data and produces Arrays of three elements corresponding to keys. The iterator may have between 0 and 4 arguments argument. The arguments are Strings that specify whether some of the data are to be returned in String or integer format.
Actually, the “each_key” iterator of ResKeyList class is identical to the “each_key” iterator of Result class.
“getData” method returns an Array of Arrays containing the data stored in a ResKeyList object. The returned Array may actually be considered as a two-dimensional Array with as many lines as there are pairs of keys in the ResKeyList object. Each line of the Array contains four elements:
The first element corresponds to the elemId.
The second element corresponds to the nodeId of the key.
The third element corresponds to the layerId of the key.
The fourth element corresponds to the subLayerId of the key.
The method may have 4, 3, 2, 1 or no argument. The arguments correspond to the type of the Array elements corresponding to elemId, nodeId, layerId or subLayerId. In the returned Array, these elements may be of String or Integer types. Correspondingly the arguments are Strings the value of which can be "int", "string" or any other String. If any other String is used as argument (for example a void string), the default Integer or String type elements are returned.
Actually, this method corresponds to the “getData” method of Result class (See section I.4.10). The special key names are the same as those listed in Tables I.4.2 to I.4.4.
One gives here a list of methods that do not fit in any category listed above:
Method “Name” attribute getter returns a String containing the name of the ResKeyList. This method corresponds to “Name” attribute.
Method “Name=” attribute setter has one String argument and sets the name of the ResKeyList. This method corresponds to “Name” attribute.
Method “Size” attribute returns an integer corresponding to the number of keys stored in the object. This method corresponds to “Size” read-only attribute.
The “Post” module contains the definition of methods belonging to no particular class. These methods are all devoted to manipulation of Results or Groups.
A list of the methods defined in “Post” module is given in Table I.6.1.
Several methods of “Post” Module allow to manipulate the information and warning messages issued by FeResPost. In C++ code, the messages are saved into a C++ ostrstream object. At the end of each FeResPost method, the content of this stream is flushed into the the output selected by the client. Several methods allow to control how information and warning messages are output:
“setInfoStreamToKeep” just keeps the information and warning messages in the ostrstream. Nothing is written to selected output.
“setInfoStreamToNone” clears the ostrstream at the end of each FeResPost method but doe not write its content anywhere.
“setInfoStreamToClientStream” sets the output to a client (ruby in this case) output stream.Tthe argument is client output stream. For ruby, it may correspond to stderr or a file that has been opened for writing.
“setInfoStreamToCppStream” sets the output to a standard C++ stream. Arguments is a String identifying the output stream. Two values are accepted: “std::cout” and “std::cerr”.
“setInfoStreamToCppFile” Selects an output corresponding to a C++ output file that is opened by FeResPost. The method has one or two arguments:
“FileName” is a String that contains the path to file that must be opened for writing.
“Mode” is a String that contains the opening mode for opeining the output file. Accepted values are “w” and “w+”. This argument is optional. Default opening mode is “w”.
“getInfoStreamContent” returns a String containing the content of information ostrstream. This method can be used when the output has been set to “keep” with “setInfoStreamToKeep” method.
“clearInfoStreamContent” clears the content of information ostrstream. This method can be used when the output has been set to “keep” with “setInfoStreamToKeep” method.
“getAndClearInfoStreamContent” returns a String containing the content of information ostrstream and clears the content of this ostrstream. (This method combines methods “getInfoStreamContent’ and “clearInfoStreamContent’.) Again, this method can be used when the output has been set to “keep” with “setInfoStreamToKeep” method.
The default standard output generally corresponds to clients (ruby, in this case) standard output. This selection is done when FeResPost library is loaded.
The redirection of standard output is useful when FeResPost is not run in “console” mode. Moreover, it is sometimes handy to separate the outputs of FeResPost from those of the ruby post-processing program. Two methods allow adding content in the selected output stream:
“writeAboutInformation” writes the FeResPost information message to standard output, or corresponding output files. (Information contains among other things the version of FeResPost and its date of compilation.)
“writeMsgOutputLine” writes a line in the standard output stream.
In section I.4.4, one defines functions that allow the creation of new Result objects from existing ones. Here, one present short-cuts to some of these functions (for the following functions, x and y are Result objects):
y=Post.exp(x) is equivalent to “y=x.deriveScalToScal("exp")”.
y=Post.log(x) is equivalent to “y=x.deriveScalToScal("log")”.
y=Post.exp10(x) is equivalent “to y=x.deriveScalToScal("exp10")”.
y=Post.log10(x) is equivalent “to y=x.deriveScalToScal("log10")”.
y=Post.abs(x) is equivalent to “y=x.deriveScalToScal("abs")”,
“y=x.deriveVectorToOneScal("abs")” or “y=x.deriveTensorToOneScal("abs")”.
y=Post.inv(x) is equivalent to “y=x.deriveScalToScal("inv")”.
y=Post.sq(x) is equivalent to “y=x.deriveScalToScal("sq")”
or “y=x.deriveVectorToOneScal("sq")”.
y=Post.sqrt(x) is equivalent to “y=x.deriveScalToScal("sqrt")”.
y=Post.sgn(x) is equivalent to “y=x.deriveScalToScal("sgn")”.
In section I.4.4, one defines functions that allow the creation of new Result objects from existing ones. Here, one present short-cuts to some of these functions (for the following functions, x, y and z are Result objects):
z=Post.pow(x,y) is generally equivalent to “z=x.deriveDyadic("pow",y)”. But the “pow” method defined in “Post” module also allows to replace the first “x” operand by a Real value. However, at least one of the two arguments must be a Result object.
z=Post.atan2(x,y) is generally equivalent to “z=x.deriveDyadic("atan2",y)”. But the “atan2” method defined in “Post” module also allows to replace the first “x” operand by a Real value. However, at least one of the two arguments must be a Result object.
z=Post.vectProduct(x,y) is generally equivalent to “z=x.deriveDyadic("vectProduct",y)”. However the first argument can be replaced by a vector (Array of three real elements). However, at least one of the two arguments must be a Result object.
z=Post.sumVectProduct(x,y) is equivalent to “z=x.deriveDyadic("sumVectProduct",y)”.
Also other functions that have no correspondence in Result class methods can be used to define new Results
z=Post.min(x,y) returns a Result build by selecting the minimum values of x and y. The method works with scalar, vectorial or tensorial results. Either x or y can be replaced by a Real value.
z=Post.max(x,y) returns a Result build by selecting the maximum values of x and y. The method works with scalar, vectorial or tensorial results. Either x or y can be replaced by a Real value.
z=Post.cmp(x,y) returns a Result build by setting the corresponding values to -1 if x<y, 0 if x==y and 1 if x>y. Both results must be scalar. Either of the two Results can be replaced by a real argument.
z=Post.mergeKeepFirst(x,y) returns a Result build by merging the two arguments. When a key is present in the two argument Results, the values extracted from the first Result are kept.
z=Post.merge(x,y) is identical to z=Post.mergeKeepFirst(x,y).
z=Post.mergeKeepLast(x,y) returns a Result build by merging the two arguments. When a key is present in the two argument Results, the values extracted from the second Result are kept.
Most of the dyadic functions insert a pair “key-value” in the created Result only if the corresponding key is found in the two Result arguments. “Post.min”, “Post.max” and the ‘Post.merge” methods are an exception: if a given key is found in only one of the two argument it is inserted in the new Result.
Five “operator” methods (functions) are defined in the “Post” module: “opAdd”, “opSub”, “opMul”, “opDiv” and “opPow”. The four first methods correspond to the four “+”, “-”, “*” and “/” operators defined in “Result”, “Group” and “ResKeyList” classes:
If first argument is a “Group” object, the second argument must also be a “Group” object.
If first argument is a “ResKeyList” object, the second argument must also be a “ResKeyList” object.
If either first or second argument is a “Result” object, then the possible arguments are those of the corresponding operators in “Result” class (section I.4.7).
The first argument can be a “Result” object, a real value, a complex value, an Array of three real values or three complex values, or a matrix of real elements.
The second argument can be a “Result” object, a real value, a complex value, an Array of three real values, or a matrix of real elements.
The “opPow” method is an alias to the “pow” method and at least one of its arguments must be a “Result” object.
Method “readGroupsFromPatranSession” reads Groups from a Patran session file and returns a Hash containing the list of Groups. The keys are Group names, and the values are the Groups. The method has two arguments:
A String corresponding to the name of the session file.
A DataBase. This argument is optional. If it is provided, the reading method removes from the created Groups all the entities undefined in the DataBase argument.
The session file from which Groups are read is as defined in section I.1.2.1. Examples of use of the method follow:
...
h=Post::readGroupsFromPatranSession("groups.ses")
...
h=Post::readGroupsFromPatranSession("groups.ses",DB)
...
Method “writeGroupsToPatranSession” is used to save groups in a Patran session file. This method does the inverse of method “Post::readGroupsFromPatranSession”. The method has two arguments:
The first argument of the method is a String containing the name of the output session file.
The second argument if the list of Groups. This can be a Hash similar to the one produced by method “Post::readGroupsFromPatranSession”, or an Array of Group objects.
When the second argument is a Hash, the String keys are used as reference names for the groups. If the second argument is an Array of Groups, their names are used in the session file.
The following statements:
...
h=Post::readGroupsFromPatranSession("groups.ses")
...
Post::writeGroupsToPatranSession("hash.ses",h)
Post::writeGroupsToPatranSession("values.ses",h.values)
...
produce equivalent Patran session files, but the order in which the Groups are defined may differ.
Two methods allow to set the verbosity level of several operations. The level of verbosity is a parameter global for FeResPost and may be used to write several information messages during operations in which the risk of inconsistent data has been deemed high. These information messages may be used to debug FeResPost, or your programs using FeResPost. Actually, the majority of programming errors you will find will be related to your own program, but the printing of FeResPost messages may help you to help find your errors. The two methods defined in “Post” Module are:
“setVerbosityLevel” has one “level” integer argument and is used to set the level of verbosity.
“getVerbosityLevel” returns an integer corresponding to the verbosity level.
The verbosity level may presently range from 0 to 2. 0 corresponds to no information messages. The amount of information messages increases with verbosity level.
Presently, the operations influenced by the verbosity level are the operations related to reading finite element models, accessing Results in disk files, Gmsh output...
Two methods are defined to convert CLA identifiers to Strings, or Strings to CLA identifiers. (See chapter II.0 for the notion of identifier.) The two methods are defined in the “Post” Module:
Examples of valid Strings corresponding to CLA identifiers:
"testLam", "15", "[15,testLam]", ...
The methods “convertBlob” returns a “Result” or “Group” object corresponding to a String argument. The String must correspond to a valid FeResPost BLOB object produced by method “toBlob” of one of the FeResPost classes.
Method “calcRandomResponse” is used to calculate a PSD and/or integrate a PSD and/or a transfert function. We summarize here the theoretical background extracted from [Sof10] that is necessary to understand what the method does. Reader is referred to [Sof10] for more information.
The purpose of a random calculation is to assess structural response as power spectral density assuming that structure behavior to a given type of excitation is known by its transfert function, and that the excitation is specified as an input power spectral density (PSD).
More precisely, one assumes that a unique excitation is present, and one calculates the response at output location :
|
|
In previous expression:
is the structure transfert function at location for an excitation . This transfert function depends on the frequency and is supposed to be obtained by computing a frequency response analysis with Nastran with a unit excitation.
is the input PSD depending on the kind of excitation and unit system used in the finite element analysis, its units are , , ... The input PSD is scalar.
is the output PSD at location . Depending on the kind of quantity that is calculated, the output PSD units may differ: for displacements, for accelerations, for stresses, for forces... FeResPost considers that the output PSD can be scalar, vectorial or tensorial depending on the kind of quantity that is calculated.
Note that the input and output PSD have always positive real values for all components.
Once a PSD is calculated, an equivalent RMS output can be calculated as follows:
|
|
Practically, FeResPost calculates the integral on a finite range of frequencies:
|
|
Practically, the transfert function is known by its values at different frequencies , . Then the integrations above are replaced by integrations on smaller frequency ranges:
|
|
Assuming a log-log dependence of between and , one has
|
|
in which
|
|
The integral in range is then calculated by:
If or :
|
|
If and :
|
|
If one assumes that function varies linearly between and , then the integral in range becomes simply:
|
|
Note that in Nastran, the assumption of log-log or linear interpolation on each frequency interval is managed by the option RMSINT. In FeResPost , the “integTyp” parameter of method “calcRandomResponse” allows choosing the type of integration. (See below.)
“calcRandomResponse” method in “Post” Module can be used to calculate output PSD from a transfert function, to integrate the PSD, and/or calculate the RMS value. The method is called as follows:
... arr=Post.calcRandomResponse(bOutputPsd,bOutputIntPsd, inputResults,freqs,psdIn,integType,addRes) psdOut=arr[0] intPsdOut=arr[1] rms=arr[2] ...
The method has 6 or 7 arguments:
“bOutputPsd” is a logical parameter that specifies whether the output PSD must be returned by the method.
“bOutputIntPsd” is a logical parameter that specifies whether the integration of the output PSD at each frequency must be returned by the method. (If one does not require the value at each frequency, only the last value is returned.)
“inputResults” is an Array of Result objects containing the transfert function (complex Result) or only its magnitude (Real result).
“freqs” is an Array of real values corresponding to the frequencies at which the transfert function and input PSD have been discretized. The size of this array must correspond to the size of the “inputResults” Array.
“psdIn” is an Array of real values corresponding to the input PSD level (excitation) at discretization frequencies. The number of elements in this Array must match the number of elements in “inputResults” and “freqs” Arrays.
“integType” is a String that specifies the interpolation and integration rule on frequency intervals. Possible values are “LogLog” or “LinLin”. If another value is provided, “calcRandomResponse” raises an exception.
“addRes” is a Real Result that must be considered as the initial value from which the integration of output PSD starts. (This parameter can be very useful when integration is “sliced” on sub-ranges of the entire frequency range.) If no starting value is specified, parameter can be omitted. If parameter is “nil”, one also considers that no starting value is specified.
Note that the different Result arguments must have the same size and keys. The method returns an Array of 3 elements:
The first element corresponds to the output PSD. It is an Array of Result objects that is filled if “bOutputPsd” argument is true. Otherwise, “nil” is returned.
The second element corresponding to the integrated output PSD:
If “bOutputIntPsd” is true, then this element is an Array of Result object corresponding to the integration at each frequency.
If “bOutputIntPsd” is false, then this element is a Result object corresponding to the last value of the integrated output PSD.
Note that the optional “addRes” parameter defines the start for the integration.
The third output corresponds to the RMS value of the output PSD. This is a Result object. Practically, the components of the output RMS are calculated as the square root of the corresponding component of the integrated output PSD. (Or the last value of the integrated output PSD, if “bOutputIntPsd” is set to “true”.)
Method “calcPredefinedCriterion” allows to calculate a pre-defined criterion “hard-coded” in C++. The parameters of the method are:
“CritName”, a String argument that specifies which criterion is required.
“InputValues”, an Array containing the arguments for the calculation. (Each argument may be a DataBase, a String an integer, a real value, a Boolean Value, a Result object, a Group object, ...)
The method returns an Array of “OutputValues” similar to the Array of input arguments.
Note that the arguments that are passed by reference in function calcPredefinedCriterion can be modified in the predefined criterion. Each predefined criterion should be documented, and the possible side effects of the method should be clearly explained.
Some advantages of using predefined criteria are listed below:
The predefined criteria give a lower level access to the FeResPost object at C++ level. This allows to perform operations on the objects that could be tricky with higher level language access, and this allows optimizations of the computations. (A marvelous example of optimization is presented in section IV.2.4.3.)
As the predefined criteria are provided in a compiled shared library, it becomes possible to hide the immplementation to the final user of FeResPost.
Once a predefined criterion is programmed and debugged, it is easier to guaranty that the same calculation is performed with ruby extension, COM component or .NET assembly.
Of course, the adoption of pre-defined criteria has also some disadvantages:
The programming of a criterion is C++ can be difficult and errors difficult to track.
The addition of a criterion, or the modification of an existing criterion requires the re-compilation of FeResPost library.
Also, if a user has developed is own pre-defined criterion, a recompilation of each new version of FeResPost is necessary to include his criterion.
So far, only a limited number of predefined criteria have been included in FeResPost. They are presented in Appendix X.C.2.
Method “loadHdf5Library” is used to load the HDF5 shared library. It is simply used as follows:
Post.loadHdf5Library("C:/NewProgs/HDF5/HDF5-1.8.20-win32/bin/hdf5.dll")
This method has been introduced in the “Post” Module, even though it is presently used only as prelude to loading results from HDF5 files in Nastran Database. We hope actually that other solves like Samcef will have the good idea to use this file format for their results.
When something wrong happens, FeResPost raises an exception with a message providing some information about the problem. Exception information can be displayed, for example, by the following code:
begin
db.readBdf("unit_xyz_V1.bdf",["../../MODEL/MESH/"],"bdf",{},true)
rescue Exception => x then
printf("\n\nMaybe you should modify the two first include statements in main file!\n")
printf("**********************************************************************\n\n")
printf("We have an exception with the following information:\n\n")
puts x.message
end
Method “getLastErrorMessage” of the “Post” module retrieves the message associated to last exception raised by FeResPost.
This chapter concerns the ruby extension only!
One class and some ruby methods are directly defined in ruby language. This part of the programming concerns the operators in which the second argument is a “Result” object, but the first argument has another type (Real, Complex, Array...). Then, a ruby type coercion is performed thanks to the “Result” class “coerce” method. This small part of code allows to perform the operations using the different “Post.op???” methods.
It seems that the built-in “Array” class defines its own “coerce” method, which conflicts with the “Result” coerce mechanism. Therefore, a modification of the “Array” class is restored in version 4.4.4 of FeResPost. (See below.)
This part of FeResPost is programmed in the “FeResPost.rb” file. content looks as follows:
# encoding: utf-8
require "FeResPost.so"
module FeResPost
class ROpResult
@x=nil
def initialize(res)
@x=res
end
def +(other)
return Post.opAdd(other,@x)
end
def -(other)
return Post.opSub(other,@x)
end
def *(other)
return Post.opMul(other,@x)
end
def /(other)
return Post.opDiv(other,@x)
end
def **(other)
return Post.pow(other,@x)
end
end
class Result
def coerce(x)
[ROpResult.new(self),x]
end
end # Result
end # FeResPost
class Array
alias _FeFesPost_old_opAdd +
alias _FeFesPost_old_opSub -
alias _FeFesPost_old_opMul *
def +(second)
if second.class==Result then
return Post.opAdd(self,second)
else
return self._FeFesPost_old_opAdd(second)
end
end
def -(second)
if second.class==Result then
return Post.opSub(self,second)
else
return self._FeFesPost_old_opSub(second)
end
end
def *(second)
if second.class==Result then
return Post.opMul(self,second)
else
return self._FeFesPost_old_opMul(second)
end
end
def /(second)
if second.class==Result then
return Post.opDiv(self,second)
else
raise "Invalid second operand for / operator"
end
end
end # Array
puts "End \"FeResPost\" module initialization.\n"
puts "\n\n"
Four classes specific to Classical Laminate Analysis calculations have been defined in FeResPost module:
The “ClaDb” class allows the definition of composite databases used to store the definition of composite materials, laminates and loadings. This class is presented in Chapter II.2.
The “ClaMat” class allows the definition and manipulation of materials. This class is presented in Chapter II.3.
The “ClaLam” class allows the definition and manipulation of laminates. This class is presented in Chapter II.4.
The “ClaLoad” class allows the definition and manipulation of loadings to be applied to laminates. This class is presented in Chapter II.5.
Throughout the composite manual pages, the concept of identifier is often used. An identifier can be:
An Integer,
A String,
Or an Array of two elements (an integer and a String).
This concept is introduced to provide a general way to identify and access materials, laminates or loads stored in a ClaDb object. Indeed, the methods used to access those data must be compatible with several software (ESAComp or finite element solvers...). As entities manipulated by these software are sometimes identified by integers, sometimes by strings and sometimes by both an integer and a String, this peculiar way to identify the entities in a ClaDb object had to be developed. For example, if a ClaLam object has been stored in a ClaDb, it can be retrieved with:
...
db.insertLaminate(lam1)
...
lam2=db.getLaminateCopy(5)
...
lam2=db.getLaminateCopy("panel1")
...
lam2=db.getLaminateCopy([5,"panel1"])
...
Note however that the identifier used to retrieve lam2 must match exactly the identifier of lam1. For example, if lam1 has [5,"panel1"] identifier, only the third “getLaminateCopy” statement works.
This leads us to a last remark about interfaces with other software. The composite classes are meant to be used with the rest of FeResPost. Among other things, it allows:
To produce layered results automatically, using the definition of laminates and, for example, Results corresponding to in-plane forces and bending moments in 2D elements,
To calculate the corresponding failure indices, strength ratios and reserve factors, all these being instances of the FeResPost::Result class.
...
The composite capabilities programming is based on the Classical Laminate Analysis as presented widely in literature. The programmer based its developments on [Gay97]. For the in-plane and flexural parts of laminate response, the approximations done in the development of equations are common to what has been found in the rest of literature. On the other hand, few references have been found about the out-of-plane shear behavior of laminates. In [Gay97], this aspect of laminate analysis is presented with a few assumptions. For example, Gay assumes a mirror symmetry of the laminate. This is obviously not a characteristic of all laminates. Therefore, the out-of-plane shear responses calculated by composite classes should be used with care.
More information about the conventions used for FeResPost composite calculations are given in Chapter II.1.
One presents below a list of limitations, which should not be considered as exhaustive:
When a mechanical loading is applied to a laminate, this loading is also characterized by an angle giving the orientation of the loading wrt the laminate. Then the definition of the loading angle follows the same conventions as the ply angle represented in Figure II.1.2. This convention for the definition of loading angle may be different of conventions used in other software. For example, ESAComp seems to consider that the angle provided for loading is the angle of the laminate wrt loading. This results in a change of sign of the corresponding angle.
As the composite classes are under development, modifications of ruby functions related to the composite classes are still possible (and likely).
The purpose of this Chapter is to summarize the classical laminate theory, and to provide the information needed by the user of composite classes to understand a few conventions that have been assumed for the programming of Classical Laminate Analysis in FeResPost (axes, angles, numbering of layers,...).
The programmer will find a presentation of the classical laminate theory that follows closely what is programmed in C++ language in FeResPost. However those who are interested in studying the theory, or who are not familiar with it are referred to more extensive presentations of the classical laminate theory [Gay97, Pal99]. Only for the out-of-plane shear behavior of the laminate, is the presentation original, even though inspired by information found in [Sof04a].
The Chapter is organized as follows:
Section II.1.1 presents the conventions used for the numbering of plies, orientations of plies, laminate axes...
Section II.1.2 summarizes the calculation rules for the rotation of tensors and vectors. Some of the notions and notations used in the rest of the Chapter are introduced in the section.
The constitutive equations describing ply materials behavior are given in section II.1.3. One also introduces several notations that are used in the rest of the Chapter and one presents the calculation rules that must be used to perform material property rotations.
In section II.1.5, the calculation of laminate in-plane and flexural properties is described. Note that the influences of temperature and moisture are not considered in the section.
Section II.1.6 is devoted to the out-of-plane shear behavior of laminates. The explanation is more detailed than what is given in section II.1.5. Here again, temperature and moisture effects are not considered.
Section II.1.7 is devoted to the influence of temperature and moisture. One considers the influence of these loading contributions on the in-plane, flexural and out-of-plane shear laminate behavior and load response.
Section II.1.8 presents the calculation of load response of laminates submitted to a loading. Among other-things, one explains how the ply stresses and strains are calculated.
Section II.1.10 is devoted to the calculation criteria available in FeResPost.
Section II.1.13 is devoted to a presentation of the units of many of the quantities introduced in this Chapter.
Figure II.1.1 represents some of the conventions used for the definition of laminate in FeResPost. The laminate coordinate system is defined in such a way that the axis is perpendicular to laminate surface and points from bottom to top surface. and vectors are parallel to the laminate plies. Plies are numbered from the bottom to the top surface. If is the index of a ply, one considers that it is limited by coordinates and . The origin of the coordinate system is located at mid laminate thickness so that if is the laminate total thickness and the laminate has plies, top surface of the laminate is located at and bottom surface at . (The plies are numbered from 1 to .)
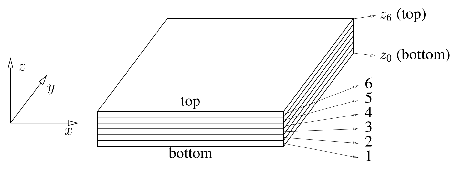
In the laminate, the plies are characterized by their material, thickness and by their angle in the laminate. Figure II.1.2 shows the convention for the orientation of a ply in a laminate. , and are the ply axes; , and are the laminate axes. Of course, because only 2D laminates are considered here, one has always . If is the angle of the ply in the laminate, this angle is as represented in Figure II.1.2: a positive angle corresponds to a rotation from axis to axis . If the angle is , the first ply axis 1 is parallel to the first laminate axis .
One common operation in classical laminate analysis is to rotate vectors, tensors and matrices. One summarizes here the operations one uses in the rest of this Chapter and in FeResPost. This rotation is represented in Figure II.1.3.
For such a rotation, the vectors and are expressed as a function of and as:
|
|
To simplify the notations, one introduces the symbols and . Also, one prefers to write the more general 3D version of the transformation:
|
| (II.1.1) |
The inverse relation corresponds to a rotation of angle and is obtained by changing the signs of the sinuses in the rotation matrix:
|
| (II.1.2) |
The expressions (II.1.1) and (II.1.2) can be used to transform the components of vectors. For example:
|
| (II.1.3) |
For the transformation of 2D tensors, the transformation matrix is used twice. For example, a Cauchy stress tensor is transformed as follows:
|
| (II.1.4) |
As the Cauchy stress tensor is symmetric, expression (II.1.4) is more conveniently written in a matricial form as follows:
|
| (II.1.5) |
The same expression applies to the components of the strain tensor, which is also symmetric:
|
|
However, unfortunately, the classical laminate analysis is universally written using angular shear components for the strain tensor:
|
|
Using the angular components, the matricial expression to be used for the rotation becomes:
|
| (II.1.6) |
An interesting aspect of the transformations (II.1.5) and (II.1.6) is that one can apply the transformation separately on sub-groups of components:
For the in-plane components, one uses the following transformations:
|
| (II.1.7) |
|
| (II.1.8) |
For the out of plane shear, the transformation is:
|
|
The relation has been written for the out-of-plane shear components of strain tensor. Note however, that the relation is the same for the out-of-plane shear components of Cauchy stress tensor.
The or component is left unchanged.
This contributes to justify some of the simplifications of the classical laminate analysis; among others, the decoupling of in-plane and flexural deformation of the laminate on one hand from the out-of-plane shear on the other hand. The third direction is systematically neglected: . The inverse of relation (II.1.7) is obviously;
|
| (II.1.9) |
|
|
In order to simplify the notations, one introduces the following notations:
|
|
|
|
|
|
|
|
|
|
|
| (II.1.10) |
These matrices are not independent. For example:
|
|
|
|
|
|
|
|
The transformations of the components of strain tensor (II.1.8) and stress tensor (II.1.9) are then written:
|
|
|
|
|
|
|
|
Similarly, for the out-of-plane shear stresses and strains one writes the following relations:
|
|
|
|
|
|
|
|
One summarizes in this section a few results that are commonly found in composite literature.
Each ply is defined by:
One material (constitutive equation),
One thickness,
One orientation wrt laminate axes,
Its allowables.
The orientation of the ply is given by an angle .
When a material is used in the definition of a laminate, assumptions are done about the axes defined in the laminate. Axes 1 and 2 are parallel to the laminate plane and axis 3 is orthogonal to the laminate.
The classical laminate analysis is based on the assumption that the relation between stress and strain tensors is linear. Then, as these two tensors are symmetric, a matrix contains all the elastic coefficients defining the material:
|
| (II.1.11) |
One shows that, because the peculiar choice of angular strain tensor components, the matrix containing the elastic coefficients is symmetric. Therefore, the matrix has only 21 independent coefficients. is the stiffness matrix of the material.
Equation (II.1.11) can be reversed as follows:
In expression (12), one added the thermo-elastic and moisture expansion terms in previous expression. They are characterized by CTE and CME tensors noted and respectively. Note that shear components of these two tensors are angular components. Practically, it does not matter much as most materials have zero shear components for CTE or CME tensors. is the compliance matrix of the material. Obviously . One often defines laminates with orthotropic materials:
For a fabric, 1 corresponds generally to the warp direction, and 2 to the weft direction. The corresponding tensile/compressive moduli are noted and respectively. denotes the out-of-plane tensile/compressive modulus.
Correspondingly, one defines shear moduli noted , and .
In general six Poisson coefficients can be defined: , , , , , . However, these coefficients are not independent. The relations
|
| (II.1.13) |
|
| (II.1.14) |
|
| (II.1.15) |
allow to eliminate the coefficients , and so that only the three Poisson coefficients , and have to be introduced when defining a material.
The constitutive equation of an orthotropic material is given by
For an isotropic material, the definition of and either or is sufficient to characterize the material. Then one has:
|
|
|
|
|
|
, and satisfy the following relation:
|
|
Finally, one introduces shorter notations that allow to rewrite expressions (II.1.11) and (12) respectively as follows:
|
| (II.1.17) |
|
|
One introduces also the “Mechanical Strain Tensor” estimated as follows:
|
| (II.1.18) |
This new strain tensor differs from the one defined by (II.1.17) by the fact that no thermo-elastic or hygro-elastic contribution is taken into account to estimate its components. It is the strain that corresponds to the actual material stress, when no thermo-elastic or hygro-elastic expansion is considered. This “Mechanical Strain Tensor” is also sometimes called “Equivalent Strain Tensor”.
One considers the properties of the ply in a plane parallel to the laminate. Then the constitutive equation (16) reduces to:
|
| (II.1.19) |
The indices in this notation are integers and indicate that the corresponding properties are given in ply coordinate system. The equation (II.1.19) is written more shortly as follows:
|
| (II.1.20) |
One introduces in (II.1.20) the material in-plane compliance matrix . In order to avoid too complicated notations, one uses the same notations as for the full material compliance matrix introduced in (II.1.17). This will be done systematically for the in-plane matricial and vectorial quantities in the rest of the document (, , , , ,...
The inverse of expression (II.1.20) is noted:
|
| (II.1.21) |
In (II.1.21) one introduces the in-plane stiffness matrix .
Plies are characterized by their orientation in the laminate. Let be the angle of the ply in the laminate axes. Then, the laminate axes are obtained by rotating the ply axes by an angle . Equations (II.1.20) and (II.1.21) are expressed in the laminate coordinate system as follows:
|
|
This leads to the new expression in laminate axes:
|
|
|
|
where one introduces new notations for in-plane ply properties rotated by an angle (in laminate axes):
|
| (II.1.23) |
|
| (II.1.24) |
|
| (II.1.25) |
|
| (II.1.26) |
|
|
|
|
When a matrix is transformed as in (II.1.23) or a vector as in (II.1.24), one says that they are rotated with rotation matrix.
One makes developments similar to those in the previous section. The out-of-plane shear constitutive equations are written as follows:
|
| (II.1.27) |
|
| (II.1.28) |
If is the angle of the ply in the laminate, the previous relations can be written in laminate axes by rotating them by an angle . For example:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Then, one makes consecutive transformations of relations (II.1.27) as follows:
|
|
where one introduced:
|
|
One says that tensor is rotated by matrix which corresponds to the expression of the shear stiffness tensor in a new coordinate system obtained by rotating the previous one by an angle .
The transformation of the out-of-plane shear compliance tensor by the same angle is made with the same expression as for the stiffness tensor:
|
|
The total laminate thickness is the sum of the thickness of each of its plies:
|
|
Correspondingly the surfacic mass is given by:
|
|
And the laminate average density is:
|
|
The classical laminate analysis is based on the assumption that in-plane and flexural behavior of the laminate is not related to out-of-plane shear loading. The corresponding laminate properties can be studied separately. The same remark is true for the load response calculation. In this section, the in-plane and flexural behavior of laminates are studied.
In this section the thermal and moisture expansions are not taken into account. The out-of-plane shear properties and loading of laminates is also discussed in a separate section. One summarizes the results of classical laminate analysis. The reader shall refer to the literature if more information on the developments that lead to these results are needed. In this section, the different equations are written in laminate axes and the corresponding indices are noted and .
Laminate compliance and stiffness matrices relate the in-plane forces and bending moments on one hand to the average strain and curvatures on the other hand. Those different quantities are defined as follows:
In-plane normal forces tensor:
|
|
Bending moment tensor:
|
| (II.1.31) |
Average deformation tensor:
|
|
Curvature tensor:
|
| (II.1.32) |
Note that average strain tensor, as well as the true tensor are not “real” tensors because their shear components (i.e. non-diagonal components are angular components.)
The relations between the four tensors are then given by two equations:
|
|
|
|
One defines below the different matrices and vectors introduced in these equations:
Matrix is a matrix corresponding to the in-plane stiffness of laminate. Its components are calculated as follows:
|
|
Matrix is a matrix corresponding to the flexural stiffness of laminate. Its components are calculated as follows:
|
|
Matrix is a matrix corresponding to the coupling between flexural and in-plane behavior of the laminate. It is calculated as follows:
|
|
All the new matrices and vectors are obtained by summation of the ply contributions. In order to obtain the ply stiffness matrix in laminate axes and the ply thermo-elastic CTE coefficients in thermo-elastic axes , one uses the transformations (II.1.24) and (II.1.26) respectively. Note however that if a ply is characterized by an orientation wrt to laminate axes, the rotation of ply properties must be of an angle .
The laminate compliance matrices , and are obtained by inversion of the matrix:
|
| (II.1.33) |
Then the average laminate strain and its curvature tensor can be calculated as follows:
|
|
|
|
One often calculates equivalent moduli corresponding to the calculated stiffness matrices and . We follow the expressions presented in [Pal99]:
One calculates the normalized in-plane, coupling and flexural stiffness and compliance matrices:
|
|
|
|
|
|
Equivalent in-plane moduli and Poisson ratios are then given by:
|
|
|
|
These moduli correspond to a case for which the laminate is free to curve under in-plane loading. This can be the case when there is coupling of in-plane and flexural laminate behavior. (Matrix is not zero.) The laminate in-plane engineering constants with suppressed curvature are calculated as follows:
|
|
|
|
|
|
Similarly, equivalent flexural moduli and Poisson ratios can be calculated. One notes the following relation:
|
|
If there is no coupling between laminate flexural and membrane properties
|
|
Generally, the “no-coupling” behavior is assumed. (See for example section II.1.6.) Therefore, one simply writes:
|
|
|
|
One presents one version of the out-of-plane shear theory for laminates based on information found in Chapter 13 of [Sof04a]. Only, one presents here a more general version of the calculation that takes and components of the out-of-plane shear stress into account at the same time.
In Chapter 13 of [Sof04a] one considers the equilibrium in direction of a small portion of the material (Figure II.1.4) of lengths and respectively:
|
|
Similarly, the equilibrium of a portion of the full laminate is given globally by the expression:
|
|
Then, in Chapter 13 of [Sof04a], developments are done to calculate the relations between and . All the developments are based on the local equilibrium relation.
In this document, a more general presentation of the out-of-plane shear behavior of laminates is done. The and components of in-plane local equilibrium are written as follows:
|
| (II.1.34) |
|
| (II.1.35) |
Correspondingly, a global equilibrium is expressed by the two equations:
|
| (II.1.36) |
|
| (II.1.37) |
Those equations shall be developed and will ultimately allow the calculation of and from the global shear and .
In most expressions below, the components of tensors are expressed in laminate axes. Therefore, the “lam” underscore is often added to the different quantities used in the equations.
First, one calculates the components of Cauchy stress tensor. However, a few simplifying assumptions shall be done. The strain tensor components are calculated from the laminate average strain tensor and curvature as follows:
|
|
|
|
|
|
(The thermo-elastic contributions have been neglected.) In most out-of-plane shear theories presented in the literature, one assumes a decoupling between in-plane load response and out-of-plane shear response. This allows us to neglect a few terms in the equations:
|
|
|
|
One then writes a simple expression of the in-plane laminate deformation tensor:
|
|
Then, the components of Cauchy stress tensor are given by:
|
| (II.1.38) |
In this last expression, the matrix corresponds to the plies in-plane moduli expressed in laminate axes. It depends on because the components generally change from one ply to another. However, one shall assume that the components of the moduli matrix are constant in each ply.
Note that, in the local and global equilibrium relations (II.1.34) to (II.1.37), only partial derivatives of bending moments and Cauchy stress tensor components appear. One assumes the decoupling between the out-of-plane shear behavior and the absolute bending in laminate. However, as shown by expressions (II.1.36) and (II.1.37), the out-of-plane shear is related to the gradient of bending moment. One derives equation (II.1.38) wrt to and :
|
|
|
|
At this point, one no longer needs to assume a dependence of the gradient of bending moments wrt and . The same is true for the gradient of Cauchy stress tensor. One also introduces a new notation:
|
|
Then, the components of Cauchy stress tensor gradient are obtained from the components of bending moments gradient with the following expression:
|
| (II.1.39) |
Note that the global equilibrium equation (II.1.36) and (II.1.37) do not contain the components and of the bending moments tensor. Similarly, the local equilibrium equations do not contain the components and of the Cauchy stress tensor. Then, these components can be considered as nil without modifying the result of the developments. The corresponding lines and columns could be removed from the equations (II.1.39).
Actually, one can do better than that. The local equilibrium equations (II.1.34) and (II.1.35) are rewritten as follows:
|
| (II.1.40) |
The substitution of (II.1.39) in (II.1.40) leads to the following expression:
This allows to find a new expression of the relation between bending moment gradients and out-of-plane shear stress. One first calculates a new matrix as follows:
|
|
is a matrix that relates the out-of-plane shear stress components partial derivatives wrt to the in-plane bending moment components:
|
| (II.1.42) |
The matrix depends on for two reasons: because of the triangular distribution of strains through the thickness, and because material moduli depend on plies material and orientation. In a given ply of index , one has:
|
|
in which the components of the two matrices and are constant. Similarly one can write a polynomial expression for if one splits the definition by plies:
Of course, one has the two relations:
|
|
|
|
The out-of-plane shear stress components are obtained by integration of expression (II.1.42) along the thickness. This leads to:
|
|
One assumes zero shear stress along the bottom surface of the laminate. This corresponds to a free surface, or at least to a surface that receives no contact forces in direction and . This assumption leads to the following expression:
in which one introduces a new matrix notation:
|
|
and a new vector notation for the gradient of bending moments:
|
|
The new matrix is of course a matrix.
An explicit expression of the integrated matrix is calculated ply-by-ply, from bottom layer to top layer. If :
In expression (II.1.44), one introduced new matrices that are calculated as follows:
|
|
|
| (II.1.45) |
|
|
Note that the expression above involve the a priori unknown quantity . To calculate this expression, one uses the continuity of across ply interfaces:
|
|
This relation corresponds to the continuity of out-of-plane shear stress at each interface between two consecutive plies. One develops the relation as follows.
The last line of this development allows to calculate recursively the components of from bottom ply to top ply. For bottom ply, the condition leads to the following expressions:
|
|
Then, it becomes possible to calculate recursively the matrices.
One checks easily that the condition ensures also that . Indeed, one has:
The last line of previous equation contains twice the integral of along the laminate thickness. One develops this integral as follows:
On the other hand, equation (II.1.33) allows to write:
(The “lam” subscript has been omitted for concision sake.) The identification of the right upper corner of the last expression with the integration of along the laminate thickness shows that this integral must be zero. Consequently, one also has:
It is interesting to remark that the ply out-of-plane shear moduli have not been used in the calculations to obtain (II.1.43). The out-of-plane shear stresses depend only on laminate in-plane bending moments and ply in-plane material properties. One shows in section II.1.6.6 that on the other hand, the calculation of out-of-plane shear strains caused by out-of-plane shear forces requires the knowledge of ply out-of-plane material constants.
Expression (41) shows that out-of-plane shear stresses in the laminate are related to partial derivatives of bending moment components, but not directly to out-of-plane shear force components. Intuitively, one would have expected a dependence of out-of-plane shear stresses on laminate out-of-plane shear forces:
Such a choice allows a reduction of size for the matrices involved in out-of-plane shear stress calculation, as one has only two components for the out-of-plane shear forces instead of 6 independent components for the gradient of bending moments.
FE solvers produce different result outputs in shell elements, as in-plane forces, in-plane bending moments and out-of-plane shear forces. They do not output gradient of in-plane bending moments however. The calculation of bending moment gradient would lead to a significant amplification of numerical errors, and to unacceptable out-of-plane shear stress results.
Previous observation might explain why most laminate analysis software calculate out-of-plane shear stresses from the out-of-plane shear forces.
In the end, we propose a calculation method based on out-of-plane shear force components because this is what most software do. The rest of this section is devoted to the presentation of different approaches to calculate dependence on shear forces.
One would like to eliminate the six and partial derivative of bending moment tensor components in the previous expression. For this, one uses the global equilibrium equations (II.1.36) and (II.1.37). This leaves some arbitrary choice in the determination of dependence wrt out-of-plane shear. For example:
The choice gives more symmetry to the relation between and . Indeed, this choice leads to:
It seems however that the choice is more common.
If the approach is adopted, one can introduce a new matrix:
This matrix allows to write a simple relation between out-of-plane shear stresses in laminate and the total out-of-plane shear force:
|
|
The matrix introduced in equation (II.1.43) also allows to introduce a new matrix:
The presentation of laminate out-of-plane shear theory in Nastran Reference Manual [Sof04a] is based on a kind of beam theory in which laminate shear response is calculated separately in directions X and Y. This corresponds to a simplification of our approach in which:
One assumes a total decoupling between the X and Y components for membrane and bending behaviour of the laminate when out-of-plane shear stresses are calculated.
No and parameters are considered in the theory.
We investigated different ways to reproduce Nastran out-of-plane shear stress calculations with FeResPost and found a few modifications that allow the calculation of out-of-plane shear stresses very similar to those produced by Nastran. We modify the calculation method as follows:
The matrix is modified in such a way that one no longer has a coupling between , and compnents. Practically, this is done by setting matrix components responsible for this coupling to zero:
|
|
(The non-diagonal components of the four matrices have been set to zero.) Note that the membrane-flexural coupling is maintained by this modification.
Corresponding to this matrix, we calculate a compliance matrix:
|
|
This new matrix has the same structure as . (, and compnents are also mutually decoupled.)
Uncoupling of , and components is also done for the material stiffness matrix :
|
|
Then, a new version of the matrix is calculated:
|
|
This new matrix also uncouples , and components of the equations.
And in the end, one no longer needs components in the calculation. Practically, this means that equation (II.1.40) becomes
|
|
and the relation between gradient of moments tensor, and out-of-plane shear forces can be written
|
|
The uncoupling also affects the calculation of out-of-plane shear stiffness matrix. (See section II.1.6.6.) In the corresponding equations in sections II.1.6.3 and II.1.6.4, matrix is replaced by . A consequence of this approximation is that the out-of-plane shear stiffness matrix is diagonal.
The “Uncoupled X-Y” approach is an impoverished version of the “” approach.
Using “” approaches, one decides that laminate axes have a special physical meaning for the composite. This choice is arbitrary however. For example, one can also write the relation between bending moments and out-of-plane shear force in a coordinate system related to the shear loading direction.
Let us define a coordinate system associated to shear loading defined as follows:
|
|
|
|
In which is shear force magnitude. In this new coordinate system, the shear force vector has only one non zero component:
|
|
Then, one can assume a simple relation between bending moments and out-of-plane shear force:
|
|
all the other components of bending moments gradient being zero. As the gradient of bending moments tensor is an order 3 tensor, previous relation can be written in laminate axes as follows:
|
| (II.1.49) |
One checks easily that this relation between shear forces and bending moments is non-linear. For example:
|
| (II.1.50) |
|
| (II.1.51) |
and
|
| (II.1.52) |
Clearly, the gradient of bending moments tensor in (II.1.52) is not the sum of corresponding tensors in (II.1.50) and (II.1.51), but the out-of-plane shear force in (II.1.52) is the sum of corresponding vectors in (II.1.50) and (II.1.51). This demonstrates the non-linearity of an approach based on a calculation in shear loading axes.
The main disadvantage of approach is that the laminate out-of-plane shear equations lose their objectivity wrt rotations of the laminate axes around axis as illustrated by the example described in section IV.3.5. (This example also allows to estimate the effects of the approximation on the precision of results given by the theory.)
On the other hand, approach leads to linear calculations, which is an advantage compared to the “resolution in shear force axes” approach. Actually, resolution in shear force axes approach is a little paradoxical wrt this aspect, as in many cases the laminate out-of-plane shear stress will be the only non-linear response of an otherwise linear problem.
This means that none of the three approaches is perfect, and the imperfections result from the fact that both approaches are approximations of the reality. Both approaches are inaccurate, and it is not possible to decide which one is better. In practical problems, one expects the three approaches give good results however.
To simplify the notations, we rewrite equation (II.1.49) as follows:
|
|
Actually, this notation also applies to the approach except that the function is then linear:
Finally, we summarize below our recommendations regarding the calculation of out-of-plane shear in laminates:
Our recommended approach is to use the “” approach with . This is the default option proposed by FeResPost.
The “uncoupled X-Y” aproach is a poorer version of the previous one. It should be used only when a very close match with Nastran results is needed.
The “resolution in shear force axes” approach advantage is that the approach is objective. Results do not depend on the choice of laminate axes. Note however that this approach leads to a non-linear dependence of ply shear stresses on the laminate loading. Also, be aware that this approach affects only the calculation of ply out-of-plane shear stresses. The laminate out-of-plane shear stiffness matrix will be the same as with “” approach
But again, the three approaches are approximate, and none of the thre appraoch is better than the other ones as far as results accuracy is concerned.
One assumes a linear relation between out-of-plane shear components of strain tensor and the corresponding components of Cauchy stress tensor:
|
|
To this relation should correspond a relation between the average out-of-plane shear strains and the out-of-plane shear force:
|
| (II.1.53) |
One attempts in this section to justify the calculation of matrix in previous expression.
By writing equation (II.1.53), one makes implicitly the assumption that there is a linear relation between the average out-of-plane shear strain tensor components and the out-of-plane shear forces tensor components. We have seen however in section II.1.6.5 that the calculation of laminate out-of-plane shear stress tensor in out-of-plane shear forces loading axes leads to a non-linear dependence of shear stresses on shear forces. A consequence of this non-linear dependence is that expression (II.1.53) is not valid if laminate out-of-plane shear equilibrium equations are solved in shear loading axes.
The developments in current section II.1.6.6 assume that the approach of section II.1.6.5 is adopted for stiffness calculations. This does not prevent us to use the “out-of-plane shear forces loading axes” approach for the calculation of ply out-of-plane shear stresses however:
We have seen in section II.1.6.5 that the approach as well as “out-of-plane shear forces loading axes” approach are both inaccurate. Calculations mixing the two approaches looses some internal consistancy, but does not lead to an increase of this inaccuracy.
Finite element solvers have adopted the approach for the calculation of laminate out-of-plane shear stiffness properties. It is no big surprise, because the calculation of laminate stiffnesses is done in solver’s code to estimate shell element properties before any information on the loading is available.
An advantage of the approach for shear stiffness calculation is that it simplifies considerably governing equations.
Also, approach allows to calculate laminate shear stiffness properties only once before load response calculations. This leads to a considerable reduction of CPU usage. The out-of-plane shear stiffness tensor is calculated wrt laminate coordinate system. Its components can then easily be obtained in any other coordinate systems by performing simple rotations.
As the purpose of FeResPost and of its composite classes is to post-process finite element results, it makes sense to adopt approaches similar to those of other finite element solvers. Remark however that other composite calculation software, like ESAComp, sometimes adopt other approaches.
In the definition of loadings, the out-of-plane components of shear force can be replaced by average out-of-plane shear stress . Then the conversion between these two types of components is done simply by multiplication or division by laminate total thickness :
|
|
One introduces notations that simplifies the writing of equations:
|
|
|
|
|
|
In these expressions the subscripts can be replaced by a symbol specific to the coordinate system in which the components of the vector are expressed (for example "load", "ply", "lam"...).
The components of matrix are easily obtained from the orientation and material of plies. The components of are obtained by a calculation of out-of-plane shear strain surface energy. One first calculates an estimate of this surface energy using the local expression of shear strains:
Note that we have used the introcuded by equation (II.1.48) in section II.1.6.5. This is possible only because we use the approach.
Surface energy can also be estimated from the out-of-plane shear global equation:
Then, as there is only one surfacic energy, and one should have
Here again, the integration can be calculated ply-by-ply. More precisely, one calculates on ply :
where
Then the integral above develops as follows:
One notes the stiffness matrix and the compliance matrix . Note that once the laminate out-of-plane shear stiffness and compliance matrices are known, the laminate out-of-plane shear equivalent moduli are calculated from the components of the compliance matrix with the following expressions:
|
|
|
|
in which the matrix has first been rotated into the appropriate axes.
One describes below the calculation sequences that is used to calculate the laminate out-of-plane shear stiffness properties, and the out-of-plane shear stresses related to a given loading of the laminate.
The calculation sequence is described below. It involves two loops on the laminate layers.
Calculate laminate in-plane and flexural properties. This is necessary because one needs the matrices and to calculate out-of-plane shear properties.
One initializes the matrix to zero.
Then for each layer with , one performs the following sequence of operations:
One estimates the matrix of in-plane stiffness coefficients in laminate axes . For other calculations, one also need properties like the laminate thickness and the positions of different layer interfaces.
This matrix is used to calculate the two matrices and . (See section II.1.6.3 for more details.) One has:
|
|
Then, one calculates two other matrices and . (See section II.1.6.3.) One has:
|
|
Then one calculates the matrices:
|
|
|
|
|
|
As the expression of is recursive, one needs another expression for the first value. The expression is:
One calculates the matrix. (See the end of section II.1.6.6 for the expressions to be used.) Then to , one adds one term:
|
|
At the end of the loop on layers, the shear stiffness matrix is calculated by inversion of .
One also defines an out-of-plane shear compliance matrix calculated as follows:
|
|
This matrix allows to calculate the laminate out-of-plane shear moduli:
|
|
|
|
Note that the values calculated above do not correspond to an out-of-plane shear stiffness of a material equivalent to the defined laminate. To convince yourself of this you can define a laminate with a single ply of orthotropic material. Then, you will observe that in which is material shear modulus. (The usual factor in shell theory is recovered.)
When the approach is adopted, matrices allow the calculation of out-of-plane shear stress from the global out-of-plane shear force:
|
|
|
|
Actually, one is interested in stresses in ply axes, rather than in laminate axes. If is the orientation of the ply in laminate axes, then:
|
|
Then, one has simply:
One stores a matrix for each station through laminate thickness where out-of-plane shear stress might be requested. Actually it is done at top, mid and bottom surfaces in each ply. This means that matrices are stored in the ClaLam object.
One first estimates the components of bending moments gradient in laminate axes with equation (II.1.49):
|
|
Then, the laminate out-of-plane shear stresses can be estimated by an expression like (II.1.43):
|
|
In this expression, is given by (II.1.44):
|
|
The three matrices , and are calculated recursively using the expressions (II.1.46), (II.1.45) and (II.1.45):
|
|
|
|
|
|
To resolve the recursion for one need an estimate for the first ply. One uses (II.1.47):
|
|
Again, one is more interested in the out-of-plane shear stresses in ply axes than in laminate axes.
One stores a matrix for each station through laminate thickness where out-of-plane shear stress might be requested. Actually it is done at top, mid and bottom surfaces in each ply. This means that matrices are stored in the ClaLam object.
One assumes a linear dependence of the temperature on the location through the laminate thickness:
|
|
Similarly, the water uptake depends linearly on :
|
|
The calculation of laminate response to hygrometric loading is very similar to its response to thermo-elastic loading. Therefore, the following developments are done for thermo-elastic loading only. Later, they are transposed to hygrothermal solicitations.
One calculates the stresses induced in plies for a thermo-elastic loading assuming that the material strain components are all constrained to zero. Equation (II.1.21) becomes:
|
|
In laminate axes, the equation is rewritten:
|
|
One substitutes in the equation the assumed temperature profile:
|
|
The corresponding laminate in-plane force tensor is obtained by integrating the Cauchy stress tensor along the thickness:
In the previous expression, two new symbols have been introduced that are calculated as follows:
Similarly the bending moment tensor is obtained by integrating the Cauchy stress tensor multiplied by along the thickness:
In the previous expression, one new symbol has been introduced:
Because of the linearity of all the equations, the thermo-elastic loading may be considered as an additional loading applied to the laminate, and if one considers an additional imposition of average in-plane strain and of a curvature, the laminate in-plane forces and bending moments are given by:
Using relation (II.1.33), the previous expression is reversed as follows:
In the last expression, four new quantities can be identified:
|
| (II.1.61) |
|
| (II.1.62) |
|
| (II.1.63) |
|
| (II.1.64) |
So that finally, the “compliance” equation is:
Starting with the out-of-plane shear constitutive equation (II.1.28) and of the expression defining the out-of-plane shear force vectors one makes developments similar to those of section II.1.7.1 and defines the following quantities:
They are used in the expression:
|
| (II.1.68) |
Correspondingly, one estimates the laminate out-of-plane shear CTE vectors:
|
| (II.1.69) |
|
| (II.1.70) |
These two expressions allow to write the expression of the inverse of (II.1.68):
|
|
One transposes below the results for thermo-elastic behavior. It is done simply by replacing the CTE by the CME in the definitions and equations.
|
| (II.1.75) |
|
| (II.1.76) |
|
| (II.1.77) |
|
| (II.1.78) |
|
|
|
| (II.1.82) |
|
| (II.1.83) |
|
|
Finally, the full set of constitutive equation written with stiffness matrices looks like:
The two previous expressions are inversed as follows:
One always considered a decoupling of in-plane and flexural of laminates on one side, and the out-of-plane shear of laminates on the other side. These two aspects are discussed in sections II.1.8.1 and II.1.8.2 respectively.
Beside thermo-elastic or hygro-elastic loading, the composite classes of FeResPost allows the definition different types of mechanical loads:
By specifying normal forces and bending moments .
By specifying average strains and curvatures .
By specifying average stresses and flexural stresses.
The type of loading is specified component-by-component. This means that a single loading may have some components imposed as normal forces and bending moments, with other components imposed as average strains, and other components as average stresses or flexural stresses. The mechanical part of loading is also characterized by a direction wrt laminate axes. The subscript “load” indicates that the components are given in loading axes. One explains below how the laminate response is calculated.
The solver first checks if average or flexural stresses are imposed. If such components of the loading are found, they are converted to in-plane forces and bending moments with the following equations:
|
|
|
|
in which is the laminate thickness.
The mechanical part of loading is characterized by a direction wrt laminate axes. This direction is given by an angle . In order to have laminate properties and loading given in the same coordinate system, the laminate stiffness matrices and CTE vectors are calculated in this new coordinate system. (It is more convenient for the elimination of components imposed as average strains or curvatures.) More precisely, the stiffness matrices and CTE vector are rotated with the following expressions:
|
|
|
|
|
|
|
|
|
|
|
|
The calculation of CTE and CME related quantities is done only if the corresponding temperature or moisture contributions have been defined in the loading. The system of equations looks like:
(Here again the CTE and CME related terms are optional.) Actually, one can write a single set of 6 equations with 6 unknowns. The general form of this system is
|
|
Now, one considers a case in which one component of vector is constrained to be a certain value. For example . This equation replaces the equation of the system:
The unknown can be easily eliminated from the linear
The first line above corresponds to a new linear system of equations with unknowns. The set of two lines define the algebraic operations that are performed in FeResPost when one imposes an average strain or curvature component.
Actually, the operation can be simplified. It is sufficient to replace line in the linear system of equations by the constraint equation and perform the “usual” Gaussian elimination to solve the linear system of equations.
When all the components of loading imposed as average strains or curvature have been eliminated from the linear system, a classical Gaussian elimination algorithm calculates the other unknowns of the system.
Then the components of tensors and are known in loading axes.
The normal forces and bending moments are then calculated in loading axes with the following equations:
(The CTE and CME related terms are optional.)
If is the angle characterizing the loading orientation wrt laminate axes a rotation of of the two vectors gives the average strain and curvature tensors in laminate axes: and .
|
|
|
|
Similarly, the normal forces and bending moments components are re-expressed in laminate axes:
|
|
|
|
For each ply, one calculates (if required) the stresses and strains as follows:
One rotates the laminate average strain and curvature tensors to obtain them in ply axes. If the ply is characterized by an angle wrt laminate axes, the two tensors are rotated by the same angle :
|
|
|
|
Note that, even though the components of these two tensors are now given in one of the plies coordinate system, they correspond to strain or curvature of the laminate at mid-thickness.
At the different stations through the thickness at which strains and stresses are required, the strain components are calculated with:
|
| (II.1.91) |
In FeResPost may have the values , , . Then the stress components are given by:
(Here again the CTE and CME related terms are optional.) A peculiar version of the ply strain tensor that corresponds to ply stresses, but without thermo-elastic or moisture contribution is calculated as follows:
|
|
This version of the strain tensor is called the “Mechanical Strain Tensor” or “Equivalent Strain Tensor”. This is the version of the strain tensors that is used for the strain failure criteria. Note however that a “Total Strain” version of the criteria is proposed as well.
At the end of the calculations, the laminate object which has been used to perform those calculations stores a few results:
The average strain and curvature of the laminate in laminate axes and .
The laminate in-plane membrane forces and bending moments in laminate axes and .
The ply results in ply axes , and , being the different stations through the thickness for which the ply results have been calculated.
The ply results may be used later to calculate failure indices or reserve factors.
Some of the quantities calculated above, and stored in the ClaLam object are used to estimate laminate shear loading response.
The different steps of the calculation are described below:
The first step of the calculation is to resolve the loading in out-of-plane shear forces in loading axes (or ). For this, one proceeds as in section II.1.5, but with the following differences: the conversion of average out-of-plane shear strain to out-of-plane shear force components requires the knowledge of out-of-plane shear stiffness matrix in loading axes. This one is readily obtained by transforming the corresponding matrix in laminate axes:
|
|
The out-of-plane shear loading can be expressed by specifying the out-of-plane shear forces, or the out-of-plane average shear strain, or a combination of the two. In all cases, the components are specified in loading axes.
If out-of-plane average shear forces are specified, the resolution of the following linear system of equations allows to calculate the corresponding out-of-plane shear strains:
(The CTE and CME related terms are optional.) The resolution of this equation is done following the same approach as for the in-plane and bending loading. One performs a Gaussian elimination in a matrix. Constraints can be imposed if out-of-plane shear strains are specified for some components of the loading instead of out-of-plane lineic shear force.
At this stage, whatever the type of loading applied to the laminate, is known. One can obtain the lineic out-of-plane shear forces with
(The CTE and CME related terms are optional.) Once and are known, the corresponding loading in laminate axes is obtained with:
|
|
|
|
For the calculation of ply out-of-plane shear stresses, one makes a distinction depending on the calculation approach that has been adopted:
With approach ply out-of-plane shear stress components are calculated at the different requested locations by:
|
|
in which the matrix is relative to the station at which the stress is requested.
If the “resolution in shear force axes” approach is adopted, one first calculates an estimate of the gradient of bending moments tensor with equation (II.1.49):
|
|
Then, ply stresses are given by
|
|
in which the matrix is relative to the station at which the stress is requested.
Finally, for the stations where out-of-plane shear stresses have been calculated the out-of-plain shear strain is also calculated using the corresponding ply material coefficients:
(The CTE and CME related terms are optional. One takes benefits of the “decoupling of out-of-plane shear” assumption.)
The Classical Lamination Theory is based on the assumption that . Consequently, and are generally not zero. These strain tensor components can be estimated from (12):
|
|
|
|
In section II.1.8, one explained the different steps to solve the laminate load response equation, and estimate ply stresses and strains. The number of operations involved in these calculations is very important, and when repetitive calculation of laminate load response is done, the computation time can increase unacceptably. This is the case, for example, when laminate load response analysis is performed on loads extracted from finite element model results.
However, many operations described in section II.1.8 will be the same for each different loading. This means that these operations could be done only once for the different laminate loads considered in the analysis. We investigate in this section the possible accelerations of laminate load response analysis.
We explain in this section how the laminate load response calculation can be accelerated. In particular, when the calculation of laminate load response is done repititively with similar loading, the benefit of simplifying the sequence of operations to estimate laminate loading becomes obvious.
One explains the calculation of laminate in-plane and flexural load response in section II.1.8.1. The sequence of operations results in the building of matrix that depends on laminate definition and loading angle. For all the calculations done with a common laminate and loading angle, the operations can be simplified as follows:
The matrix is assembled.
The components of loading that are specified as in-plane strain, or curvature lead to the imposition of constraints on matrix . For example, if one imposes , it is sufficient to replace the elements of line in matrix by 0, except =1. When all the constraints have been imposed, one obtains a new matrix that we call .
Finally, this matrix is inversed, and on obtained the matrix .
This matrix is the same for all the loadings that we apply with on the same laminate, with the same loading angle , and with the same constraints. When calculating load response, this matrix is used as follows:
For each laminate load, one assembles the 6 components vector as explained in section II.1.8.1. The components usually correspond to shell forces or moments, but the “constrained components” (components specified as strains or curvature) are replaced by components of shell in-plane strains or curvatures.
Shell in-plane strains and curvatures in loading axes are obtained by calculating the following matricial product:
|
|
Then, the shell strains and curvature components can be expressed in laminate axes by performing the following matricial operation:
Finally, the last expression leads to the definition of a new matrix
|
|
that allows to write
|
| (II.1.97) |
This matrix can be constructed once and for all for a given laminate, loading angle and loading characteristics.
A similar approach can be used for the simplification of the laminate out-of-plane shear response calculation:
The construction of a matrix allows to write:
|
|
in which corresponds to the out-of-plane shear loads (forces or strains).
Then
|
|
And this leads to the definition of a new matrix that allows to write:
|
|
|
| (II.1.98) |
Finally, now that the laminate strains and curvatures have been estimated in laminate axes, the corresponding laminate forces and moments are estimated as follows:
One can substitute (II.1.97) and (II.1.98) in expressions (99) and (100). This leads to the following expressions:
From equations (II.1.97), (II.1.98), (101) and (102), one identifies four matrices and four vectors that allow the calculation of laminate stress/strain state in laminate axes:
The matrix ,
The matrix ,
The matrix ,
The matrix ,
The 6-components vector ,
The 2-components vector ,
The 10-components vector ,
The 6-components vector .
The four matrices depend on laminate definition, angle of the loading wrt laminate axes, and on the set of components that are constrained to strain or curvature values. The four vectors also depend on the values of the particular loading that is examined. This means that the four matrices can be calculated once and for all the particular loadings. On the other-hand the four vectors must be re-estimated for each element defining the load.
The calculation of ply stresses and strains from the laminate loads is easily accelerated. Indeed, let us consider a laminate loading corresponding to:
Laminate in-plane average strain and curvature tensors and (in laminate axes),
Laminate bending gradient (in laminate axes),
Laminate temperature loading characterized by the two real values and ,
Laminate moisture loading characterized by the two real values and .
These quantities correspond to 16 real values that characterize entirely the laminate loading. For a given ply, the stresses can be calculated at a given height ( value) from these 16 real values. All the calculations are linear.
If one defines a vector with 16 components as follows:
|
|
That contains all the laminate loading, there must be a matrix that allows to calculate ply stresses as follows:
|
|
Matrix is a matrix that depends only on laminate definition. This means that this matrix can be calculated once and for all when laminate is created in the database.
Similarly one can also define matrices and for the calculations of and respectively. We explain here, how these three matrices can be constructed.
The first step of ply stresses or strain calculations consists in expressing the laminate loading in ply axes. The following operations are performed:
|
|
|
|
|
|
The four real values corresponding to laminate temperature and moisture loading are not affected by the modification of coordinate system. The three relations above allow us to write the following equation:
|
| (II.1.103) |
Note that the out-of-plane shear response is now expressed as out-of-plane shear stresses at the specified height in selected ply and no longer as laminate out-of-plane shear forces.
The strains, temperatures and moisture at height in selected ply is easily obtained with the following expressions:
|
|
|
|
|
|
The combination of these three expressions in a single matricial expression gives:
|
| (II.1.104) |
( and are and unit matrices respectively.) Then, considering equation (92), one writes:
|
| (II.1.105) |
The vector at left hand side of expression (II.1.105) contains all the ply stress components. One can remove the two lower lines of the equation as follows:
|
| (II.1.106) |
Then, the components can be reordered as follows:
|
| (II.1.107) |
One will also use:
|
| (II.1.108) |
One uses (12) to estimate the strain tensor:
|
| (II.1.109) |
The vector that appears in right-hand-side of the previous expression The so-called “mechanical strain tensor” is given by:
|
| (II.1.110) |
All the operations (II.1.103) to (II.1.110) reduce to matricial products. The characteristics of the matrices used in these operations are summarized in Table II.1.1. Two of these matrices are “re-ordering” metrices, and do not depend on the ply material or position accross laminate thickness. The other matrices depend on the ply material. Only two of the matrices depends on height .
In the end, one writes:
We have shown that if one wishes to calculate stresses and strains in plies from the laminate loading , at the three “bot” “mid” and “sup” heights of laminate plies, one needs to calculate matrices per ply. Each of the matrices has size and depends only on the laminate definition. This means that these matrices can be calculated once and for all when laminate is defined.
Note that the acceleration matrices for the ply stresses and strains calculation must be re-estimated each time the laminate or one of its materials is modified. This is the reason why method “reInitAllPliesAccelMatrices” has been added to the “ClaLam” and “ClaDb” classes.
Finally, as usual, the out-of-plane shear calculation approach will influence the results, because the gradient of bending tensor can be calculated different ways:
With approach, one calculates:
|
| (II.1.114) |
If the “resolution in shear force axes” approach is adopted, this vector is given by:
|
|
The adoption of the first or second approach affects only the corresponding components of vector. Matrices , and remain the same.
When stresses and strains have been calculated in plies (or some of the plies), the failure indices can be estimated too. One presents below the different failure theories that are proposed in FeResPost, and how these failure theories can be used to estimate laminate reserve factors.
In this section, one conventionally uses integer subscripts to denote that tensor components are given in ply axes and Roman subscripts to indicate principal components. Often, only in-plane components of ply stress or strain tensors are used to estimate criteria. Then, the principal components are estimated as follows:
|
|
In the rest of this section all the allowables used in failure criteria have positive values. Even the compressive allowables are .
Table II.1.2 summarizes the criteria available in FeResPost. For each criterion, the Table provides:
A String corresponding to the argument that identifies the selected criterion when derivation is asked.
A description of the type of material (metallic or isotropic, unidirectional tape, fabric,...).
A reference to the section in which the criterion is presented and discussed.
Specification whether an equivalent stress for this criterion can be derived in FeResPost or not.
One specifies whether a failure index can be derived with FeResPost. Generally, the failure index is calculated according to the “usual” definition in litterature. when no such standard failure index definition is available, one provides a default definition which corresponds to the inverse of the reserve factor calculated with .
One specifies whether a reserve factor and/or strength ratio can be calculated with FeResPost:
The “reserve factor” (RF) can be defined as the factor by which laminate loads can be multiplied to reach the threshold of composite failure according to the selected failure criterion. A safety factor is included in the calculation of reserve factor.
The “strength ratio” (SR) is defined as the inverse of the reserve factor. Here again; the factor of safety is taken into account for the calculation of strength ratio.
| Criterion | Material | Section | Derived | ||
| Name | Type | Number | Stress | F.I. | R.F. and S. R. |
| “Tresca2D” | metallic | II.1.10.1 | yes | yes | yes |
| “VonMises2D” | metallic | II.1.10.2 | yes | yes | yes |
| “VonMises3D” | metallic | II.1.10.3 | yes | yes | yes |
| “MaxStress” | tape or fabric | II.1.10.4 | no | yes | yes |
| “MaxStress3D” | tape or fabric | II.1.10.5 | no | yes | yes |
| “MaxStrain” | tape or fabric | II.1.10.6 | no | yes | yes |
| “MaxStrain3D” | tape or fabric | II.1.10.7 | no | yes | yes |
| “CombStrain2D” | tape or fabric | II.1.10.8 | no | yes | yes |
| “MaxTotalStrain” | tape or fabric | II.1.10.6 | no | yes | yes |
| “MaxTotalStrain3D” | tape or fabric | II.1.10.7 | no | yes | yes |
| “CombTotalStrain2D” | tape or fabric | II.1.10.8 | no | yes | yes |
| “TsaiHill” | fabric | II.1.10.9 | no | yes | yes |
| “TsaiHill_b” | fabric | II.1.10.10 | no | yes | yes |
| “TsaiHill_c” | fabric | II.1.10.11 | no | yes | yes |
| “TsaiHill3D” | fabric | II.1.10.12 | no | yes | yes |
| “TsaiHill3D_b” | fabric | II.1.10.13 | no | yes | yes |
| “TsaiWu” | fabric | II.1.10.14 | no | yes | yes |
| “TsaiWu3D” | fabric | II.1.10.15 | no | yes | yes |
| “Hoffman” | fabric | II.1.10.16 | no | yes | yes |
| “Puck” | tape | II.1.10.17 | no | yes | yes |
| “Puck_b” | tape | II.1.10.18 | no | yes | yes |
| “Puck_c” | tape | II.1.10.19 | no | yes | yes |
| “Hashin” | tape | II.1.10.20 | no | yes | yes |
| “Hashin_b” | tape | II.1.10.20 | no | yes | yes |
| “Hashin_c” | tape | II.1.10.20 | no | yes | yes |
| “Hashin3D” | tape | II.1.10.21 | no | yes | yes |
| “Hashin3D_b” | tape | II.1.10.21 | no | yes | yes |
| “Hashin3D_c” | tape | II.1.10.21 | no | yes | yes |
| “YamadaSun” | tape | II.1.10.22 | no | yes | yes |
| “YamadaSun_b” | fabric | II.1.10.23 | no | yes | yes |
| “Honey3D” | honeycomb | II.1.10.24 | no | yes | yes |
| “HoneyShear” | honeycomb | II.1.10.25 | no | yes | yes |
| “HoneyShear_b” | honeycomb | II.1.10.26 | yes | yes | yes |
| “Ilss” | all | II.1.10.27 | yes | yes | yes |
| “Ilss_b” | all | II.1.10.27 | yes | yes | yes |
Note that many of the criteria presented here are particular cases of a general quadratic criterion that requires first the calculation of a failure index:
then a test is done on the calculated value:
|
|
This means that no failure occurs if (ply or laminate passes the failure test) and one has failure if .
Several failure theories discussed below are obtained by expressing the coefficients in the expressions above by expressions depending on the material allowables. Also for the Tsai-Wu criteria discussed in section II.1.10.14 and II.1.10.15, the parameters are directly characterized for the material.
Note that the 2D criteria defined in this section often correspond to the failure criteria defined in ESAComp.
| ESAComp failure criterion | CLA criterion ID | section |
| “Maximum Shear Stress (Tresca)” | “Tresca2D” | II.1.10.1 |
| “Von Mises” | “VonMises2D” | II.1.10.2 |
| “Maximum Strain” (in ply axes) | “MaxStrain” | II.1.10.6 |
| “Maximum Stress” (in ply axes) | “MaxStress” | II.1.10.4 |
| “Tsai-Wu” | “TsaiWu” | II.1.10.14 |
| “Tsai-Hill” | “TsaiHill” | II.1.10.9 |
| “Hoffman” | “Hoffman” | II.1.10.16 |
| “Simple Puck” | “Puck” | II.1.10.17 |
| “Modified Puck” | “Puck_b” | II.1.10.17 |
| “Hashin” | “Hashin” | II.1.10.20 |
Using the stress tensor components a scalar equivalent shear stress is given by:
|
|
Ply passes the failure criterion if
|
|
This equivalent shear stress allows to define a Tresca failure index as follows:
|
|
The reserve factor is given by:
|
|
and the strength ratio by:
|
|
This criterion is referred to as “Tresca2D” criterion in FeResPost.
Using the stress tensor components a scalar equivalent shear stress is given by:
|
|
Ply passes the failure criterion if
|
|
The corresponding failure index is:
|
| (II.1.116) |
The reserve factor is given by:
|
| (II.1.117) |
and the strength ratio by:
|
| (II.1.118) |
This criterion is referred to as “VonMises2D” criterion in FeResPost.
Using the stress tensor components a scalar equivalent shear stress is given by:
|
|
Ply passes the failure criterion if
|
|
As for the 2D version, the corresponding failure index is given by II.1.116, the reserve factor by II.1.117 and the strength ratio by II.1.118. This criterion is referred to as “VonMises3D” criterion in FeResPost.
The failure index is calculated as follows:
|
|
in which the and allowables depend on the sign of and respectively. (Generally, tensile and compressive allowables are different for orthotropic materials.) Ply passes the test if the three following conditions are satisfied:
|
|
|
|
|
|
The reserve factor is calculated as follows:
|
|
and the strength ratio is given by:
|
|
This criterion is referred to as “MaxStress” criterion in FeResPost.
The failure index is calculated as follows:
|
|
in which the , and allowables depend on the sign of , and respectively. (Generally, tensile and compressive allowables are different for orthotropic materials.) Ply passes the test if the six following conditions are satisfied:
|
|
|
|
|
|
|
|
|
|
|
|
The reserve factor is calculated as follows:
|
|
and the strength ratio is given by:
|
|
This criterion is referred to as “MaxStress3D” criterion in FeResPost.
The criterion is very similar to maximum stress criterion, except that it is calculated from the mechanical (or equivalent) strain tensor components. The failure index is calculated as follows:
|
|
in which the and allowables depend on the sign of and respectively. Ply or laminate passes the test if the three following conditions are satisfied:
|
|
|
|
|
|
The reserve factor is calculated as follows:
|
|
and the strength ratio is given by:
|
|
This criterion is referred to as “MaxStrain” criterion in FeResPost.
FeResPost proposes a second version of the criterion where the “total” strain tensor is used instead of the mechanical strain tensor . This version of the criterion is referred to as “MaxTotalStrain” criterion in FeResPost.
The criterion is very similar to maximum stress criterion, except that it is calculated from the mechanical (or equivalent) strain tensor components. The failure index is calculated as follows:
|
|
in which the , and allowables depend on the sign of the corresponding mechanical strain tensor component. Ply or laminate passes the test if the six following conditions are satisfied:
|
|
|
|
|
|
|
|
|
|
|
|
The reserve factor is calculated as follows:
|
|
and the strength ratio is given by
|
|
This criterion is referred to as “MaxStrain3D” criterion in FeResPost.
FeResPost proposes a second version of the criterion where the “total” strain tensor is used instead of the mechanical strain tensor . This version of the criterion is referred to as “MaxTotalStrain3D” criterion in FeResPost.
The criterion is a strain criterion that uses a combination of several components of the strain tensor. This criterion can be considered as a Tsai-type criterion adapted to strain tensor. The combined strain failure index is calculated as follows:
|
|
in which the and allowables depend on the sign of and respectively. (The criterion is calculated from the mechanical or equivalent strain tensor components.) Ply or laminate passes the failure criterion if the two following conditions are respected:
|
|
|
|
The reserve factor is calculated as follows:
|
|
and the strength ratio is given by:
|
|
This criterion is referred to as “CombStrain2D” criterion in FeResPost.
FeResPost proposes a second version of the criterion where the “total” strain tensor is used instead of the mechanical strain tensor . This version of the criterion is referred to as “CombTotalStrain2D” criterion in FeResPost.
The Tsai-Hill criterion is a quadratic criterion. The 2D version of this criterion has a failure index calculated as follows:
|
|
Here again, the allowables and depend on the signs of and respectively. Ply passes the failure criterion if
|
|
The Tsai-Hill failure index depends quadratically on the different components of the stress tensor. Therefore, the reserve factor is calculated as follows:
|
| (II.1.119) |
and the strength ratio is given by:
|
| (II.1.120) |
This criterion is referred to as “TsaiHill” criterion in FeResPost.
This criterion is very similar to the one described in section II.1.10.10. It differs by the fact that only the tensile allowables and are considered for the calculations.
The calculation of reserve factor is as for the more classical Tsai-Hill criterion (II.1.119) and (II.1.120). This criterion is referred to as “TsaiHill_b” criterion in FeResPost.
This criterion is very similar to the one described in section II.1.10.9. The criterion has a failure index calculated as follows:
|
|
The criterion differs from the previous one by the fact that the allowable is used in the calculation. This allowable is set to or depending on the sign of .
The calculation of reserve factor is as for the more classical Tsai-Hill criterion (II.1.119) and (II.1.120). This criterion is referred to as “TsaiHill_c” criterion in FeResPost.
The Tsai-Hill criterion is a quadratic criterion. The 3D version of this criterion has a failure index calculated as follows:
The allowables , and depend on the signs of , and respectively. Ply passes the failure criterion if
|
|
The Tsai-Hill failure index depends quadratically on the different components of the stress tensor. The reserve factor is calculated as follows:
|
| (II.1.122) |
and the strength ratio is given by:
|
| (II.1.123) |
This criterion is referred to as “TsaiHill3D” criterion in FeResPost.
This criterion is very similar to the one described in section II.1.10.13. It differs by the fact that only the tensile allowables , and are considered for the calculations.
The calculation of reserve factor is as for the more classical Tsai-Hill criterion (II.1.122) and (II.1.123). This criterion is referred to as “TsaiHill3D_b” criterion in FeResPost.
The Tsai-Wu criterion is a quadratic criterion. The 2D version of this criterion has a failure index calculated as follows:
In this expression, is a material parameter to be obtained by characterization tests. This parameter must satisfy the following relation:
|
| (II.1.125) |
Its units are, for example, . Sometimes the corresponding dimensionless parameter is used instead:
|
| (II.1.126) |
This dimensionless parameter must satisfy the relation:
|
| (II.1.127) |
The value corresponds to a generalized Von Mises criterion. The value
|
| (II.1.128) |
leads to the Hoffman criterion discussed in section II.1.10.16. Ply passes the failure criterion if
|
|
In some of the terms of expression (124) the components of Cauchy stress tensor appear linearly, and other terms, they appear quadratically. Therefore, the reserve factor expression is a little more complicated. FeResPost calculates it as follows:
|
|
|
|
|
|
|
|
and the strength ratio is given by:
|
|
This criterion is referred to as “TsaiWu” criterion in FeResPost.
The 3D version of Tsai-Wu failure criterion leads to the following expression of the failure index:
The values of and are submitted to the same limitations as in section II.1.10.14. Ply passes the failure criterion if
|
|
The RF calculation is done as follows:
|
|
|
|
|
|
and the strength ratio is given by:
|
|
This criterion is referred to as “TsaiWu3D” criterion in FeResPost.
The Hoffman criterion is very similar to the Tsai-Wu criterion. Only the last term of failure index is different:
Ply passes the failure criterion if
|
|
In some of the terms of previous expression the components of Cauchy stress tensor appear linearly, and other terms, they appear quadratically. Therefore, the reserve factor expression is a little more complicated. FeResPost calculates it as follows:
|
|
|
|
|
|
|
|
and the strength ratio is given by:
|
|
This criterion is referred to as “Hoffman” criterion in FeResPost.
This criterion is adapted to the justification of laminates with unidirectional plies. This criterion distinguishes two failure mode: one fiber failure mode in direction 1 and one matrix failure mode. One distinguishes three versions of the Puck criterion.
The first version of Puck failure index is calculated as follows:
|
|
in which the allowables and depend on the signs of and respectively. Ply passes the failure criterion if the two following conditions are satisfied
|
|
|
|
The reserve factor is simply given by:
|
|
and the strength ratio is given by:
|
|
This criterion is referred to as “Puck” failure criterioncriterion in FeResPost.
A modified version of Puck criterion is defined as follows:
|
|
Ply passes the failure criterion if the two following conditions are satisfied
|
|
|
|
The reserve factor is calculated as follows:
|
|
|
|
|
|
|
|
|
|
|
|
The calculation of failure index is based on the calculation of the reserve factor:
|
|
in which the safety factor used in the calculation of the RF is 1. The advantage of this new expression is that the failure index is proportional to the components of stress tensor. This criterion is referred to as “Puck_b” criterion in FeResPost.
For the strength ratio, one uses the same expression, but the safety factor is not set to 1:
|
|
Sometimes, an additional term is given in the expression corresponding to the fiber failure and the modified version of Puck criterion is defined as follows:
|
|
Ply passes the failure criterion if the two following conditions are satisfied
|
|
|
|
The calculation of reserve factor is done as for version “b” of Puck criterion, but one uses a modified expression for parameter:
|
|
This criterion is referred to as “Puck_c” criterion in FeResPost.
This criterion is meant to be used for uni-directional materials. Direction 1 is assumed to be direction of fibers. One first presents the way the reserve factor is calculated:
If , ply passes the failure criterion if the following condition is satisfied:
|
|
Reserve factor is given by:
|
|
If , ply passes the failure criterion if the following condition is satisfied:
|
|
The corresponding reserve factor is
|
|
The calculation of matrix failure is slightly more complicated. if , ply passes the failure criterion if the following condition is satisfied:
|
|
one has simply:
|
|
Otherwise, ply passes the failure criterion if the following condition is satisfied:
|
|
A quadratic equation is solved to obtain the corresponding reserve factor.
|
|
|
|
|
|
|
|
Finally, the reserve factor is given by:
|
|
Here again, the calculation of failure index is based on the calculation of the reserve factor:
|
|
in which the safety factor used in the calculation of the RF is 1, and the strength ratio is calculated as
|
|
in which one keeps the value of safety factor.
The criterion presented above is referred to by “Hashin” criterion in FeResPost. Correspondingly, one defines version “Hashin_b” in which only the fiber failure is checked and “Hashin_c” in which only the matrix failure is checked. (These correspond to the values and calculated above.)
A 3D version of the 2D criterion defined in section II.1.10.20 is defined as follows
If , ply passes the failure criterion if the following condition is satisfied:
|
|
and reserve factor is given by:
|
|
If , ply passes the failure criterion if the following condition is satisfied:
|
|
The corresponding reserve factor is
|
|
The calculation of matrix failure is slightly more complicated. If ply passes the failure criterion if the following condition is satisfied:
|
|
Reserve factor is then given by:
|
|
Otherwise, ply passes the failure criterion if the following condition is satisfied:
|
|
For that case, one successively calculates:
|
|
|
|
|
|
|
|
Finally, the reserve factor is given by:
|
|
Here again, the calculation of failure index is based on the calculation of the reserve factor:
|
|
in which the safety factor used in the calculation of the RF is set to 1, and the strength ratio is calculated as
|
|
in which one keeps the value of safety factor.
The criterion presented above is referred to by “Hashin3D” criterion in FeResPost. Correspondingly, one defines version “Hashin3D_b” in which only the fiber failure is checked and “Hashin3D_c” in which only the matrix failure is checked. (These correspond to the values and calculated above.)
The Yamada-Sun criterion is a kind of Tsai criterion adapted to tape (unidirectional) materials. Its failure index is calculated as follows:
|
|
The allowable depends on the sign of . Ply passes the failure criterion if the following condition is satisfied
|
|
The reserve factor is calculated as follows:
|
|
and the strength ratio is given by:
|
|
This criterion is referred to as “YamadaSun” in FeResPost.
A second version of Yamada-Sun criterion more adapted to fabrics is proposed. The “tape” version of Yamada-Sun criterion is calculated in two directions, and the worst direction is considered for failure. The failure index is calculated as follows:
|
|
The allowables and depends on the signs of and respectively. Ply passes the failure criterion if the two following conditions are satisfied:
|
|
|
|
The reserve factor is calculated as follows:
|
|
and the strength ratio is given by:
|
|
This criterion is referred to as “YamadaSun_b” in FeResPost.
A general honeycomb criterion uses the out-of-plane tension/compression and the two out-of-plane shear components of the Cauchy stress tensor. The criterion read as follows:
|
|
The allowable depends on the sign of (Generally, the compressive allowable is significantly smaller than the tensile one). The honeycomb material is generally defined in such a way that the allowable is in ribbon direction (longitudinal allowable) and is the transverse allowable . Core passes the failure criterion if the following condition is satisfied
|
|
The reserve factor is calculated as follows:
|
|
and the strength ratio is given by:
|
|
This criterion is referred to as “Honey3D” in FeResPost.
Depending of the modeling, the component of Cauchy stress tensor is sometimes zero. Then a simplified “shear” criterion is often used:
|
|
Core passes the failure criterion if the following condition is satisfied
|
|
The reserve factor is calculated as follows:
|
|
and the strength ratio is given by:
|
|
This criterion is referred to as “HoneyShear” in FeResPost.
Sometimes, one simplifies the criterion described in section II.1.10.25 by using the smallest shear allowable . This new criterion is referred to as “HoneyShear_b”.
As a single allowable is used, an equivalent shear stress can be defined:
|
| (II.1.132) |
The failure index is then calculated as follows:
|
|
Core passes the failure criterion if the following condition is satisfied
|
|
The reserve factor is calculated as follows:
|
|
and the strength ratio is given by:
|
|
This criterion is referred to as “HoneyShear_b” in FeResPost.
The inter-laminar shear criterion is based on the comparison of inter-laminar shear stress with resin shear allowable:
|
|
In which the inter-laminar shear stress is a scalar stress calculated as follows:
|
| (II.1.133) |
An interface between two plies passes the failure criterion if the following condition is satisfied
|
|
The reserve factor is of course:
|
|
and the strength ratio is given by:
|
|
This criterion is different from the other criteria in this that it does not use ply material allowables. Instead, the ply ilss allowable or the laminate ilss allowable is used.
Note also that FeResPost calculates the inter-laminar shear criterion on the lower face of plies only. This criterion is referred to as “Ilss” in FeResPost.
A second version of the inter-laminar shear stress criterion, referred to as “Ilss_b” criterion in FeResPost, is defined in FeResPost. This criterion differs from the more usual “Ilss” criterion by the fact that its calculation is not limited to the lower face of laminate plies. It can also be calculated at mid-ply or ply upper face. This can be handy when one wishes to evaluate the ILSS criterion on finite element results that are extracted at mid ply thickness only. (Actually, the calculation of ILSS failure criterion using stresses extracted from FE results, or calculated from FE shell forces and moments, is the reason that has justified the introduction of this second version of ILSS criterion.)
The thermal conservation equation in a solid material is written as follows:
|
|
where is the temperature, is the heat capacity of the material and vector is the heat flux. Note that and are used for transient thermal calculations only. Generally, the heat flux is related to the gradient of temperature by Fourrier’s law:
|
|
where is the tensor of thermal conductivity coefficients. We consider that thermal conductivity tensor is symmetric. A justification of this symmetry can be found in [LLK86] with part of the demonstration in [LL13].
When thermal conductivity calculations are performed with laminates, two homogenized quantities must first be calculated:
The laminate global conductivity tensor,
The laminate global thermal capacity.
These two quantities are obtained by integrating material properties along laminate thickness.
Two scalar parameters influence the transient thermal behavior of laminates: the density and the heat capacity (per unit of mass) . As these two parameters are scalar, their characteristics do not depend on the possible anisotropy of the material.
On the other hand, the thermal conductivity is a order tensor. Generally, for an anisotropic material, the thermal conductivity equation can be written as follows:
|
|
For an orthotropic material, the previous equations reduces to:
|
|
Then, only three material parameters define the thermal conductivity. Finally, for an isotropic material the thermal conductivity is defined by a single parameter :
|
|
As has been done for the motion equations, one assumes a decoupling of in-plane laminate thermal conductivity and out-of-plane conductivity. Therefore, the thermal flux is separated into an in-plane flux:
|
|
and the out-of-plane component .
Correspondingly, the tensor of thermal conductivity coefficients is separated into an in-plane conductivity tensor:
|
|
and the out-of-plane conductivity . The “shear” components and are neglected in the homogenization theory. (This means that out-of-plane and in-plane conductivities are decoupled.)
The material scalar properties are left unmodified by in-plane rotations. The same is true for the out-of-plane quantities and . The transformation of components for and is noted with the transformation matrices defined in expressions (II.1.10) to (II.1.10):
|
|
|
|
|
|
|
|
One considers separately the laminate thermal in-plane conductivity, thermal out-of-plane conductivity and thermal capacity.
To calculate the laminate in-plane thermal conductivity properties, one assumes that temperature is constant along the laminate thickness. Consequently, the temperature gradient does not depend on . The thermal flux however depends on because the thermal conductivity does:
|
|
The laminate in-plane thermal conductivity is calculated as follows:
In the previous equation, one introduced the laminate in-plane thermal conductivity:
where is the thickness of ply .
One assumes that out-of-plane thermal flux is constant across laminate thickness. Then, as thermal conductivity depends on , so will the out-of-plane gradient of temperature:
|
|
The integration across the thickness gives the difference of temperature between upper and lower laminate surfaces:
In previous expression, one introduced the out-of-plane thermal resistance:
To estimate the laminate thermal capacity, one again assumes a temperature constant across the laminate thickness. Then, the heat energy stored per unit of surface is:
In previous expression, one introduced the surfacic thermal capacity
Note that in Nastran, when a thermal material MAT4 or MAT5 is defined, the density and the heat capacity per unit of mass are defined separately. So it is the responsibility of the user to select appropriate values for these two quantities. Also, in Nastran, the thickness is defined separately in the PSHELL property card. (PCOMP or PCOMPG cards do not accept thermal materials.)
The moisture conservation equation in a solid material is written as follows:
|
|
where is the moisture content (for example in [kg/m]) and vector is the massic flux of moisture (in [kg/ms]). When several materials are present in a structure, as often in laminates, it is more practical to work with moisture percentage (in [%w]). The moisture percentage is related to moisture content by the following expression:
|
|
where is the moisture coefficient in [kg/(m%w)].
Generally, the moisture flux is related to the gradient of moisture by Fick’s law, and the moisture diffusion equation can be written:
|
|
Here is the tensor of moisture conductivity coefficients. This expression is very similar to the equation of thermal diffusion:
The components of are defined the same way as the components of depending on the type of material (isotropic, orthotropic or anisotropic).
The calculation of laminate global conductivity properties is done the same way as for thermal conductivities:
|
|
|
|
As one works with moisture percentages, nothing equivalent to the laminate thermal capacity is defined for moisture.
All the quantities introduced in this Chapter have been given without dimensions. Since version 3.0.1, units can be attributed to all the CLA quantities defined in FeResPost, except of course the dimensionless quantities. This allows the user to express all the CLA quantities in a units system compatible, for example, with the unit system used for finite element modeling.
An engineer should be able to figure out the units of the different quantities introduced in this Chapter from the definitions given for the quantities or from the expressions used for their calculations. However, we think it might be useful to remind the units of the different quantities to avoid ambiguities.
In the rest of the section, one assumes a consistent set of units compatible with MKS system is used. This is what we recommend for FeResPost, as well as finite element models. The default “base” units are:
Lengths are expressed in meters [m].
Masses are expressed in kilograms [kg].
Time is expressed in seconds [s].
Force is expressed in Newtons [N].
Energy is expressed in joules [J].
Temperatures are expressed in Celsius degrees [C].
Moisture contents are expressed in percentage of weight [%w]. (Weight of water divided by the weight of dry material in %.)
One notes that units have been defined for force and energy, despite the fact that they can be derived from mass, length and time units. Practically, the definition of additional base units for the force and energy are of interest for mechanical engineers.
All the other units of FeResPost are obtained by combining these base units. The most important ones are summarized in Tables II.1.4, II.1.5 and II.1.6.
If one of the base units above is modified, the user is responsible for modifying the derived units coherently. For example, we expressed the moisture content in [%w]. This influences the units of moisture content as well as the units of coefficients of moisture expansion .
| Quantities | Symbols | Units |
| Strains | , or | [L/L] or [-] |
| Stresses | or | [F/L] |
| Curvatures | [1/L] | |
| Forces | or | [F/L] |
| Moments | [FL/L] or [F] | |
| Temperatures | [T] | |
| Moistures | [W] (always [%w]) | |
| Failure indices | [] | |
| Reserve factors | [] | |
| Quantities | Symbols | Units |
| Materials stiffnesses or moduli | , , or | [F/L] |
| Materials compliance matrices | , , | [L/F] ] |
| Poisson coefficients | [-] | |
| Thermal conductivity | [E/(LT)] | |
| Coefficients of thermal expansion | [L/(LT)] or [1/T] | |
| Moisture conductivity | [1/(Lt)] | |
| Coefficients of moisture expansion | [L/(LW)] or [1/W] | |
| Density | [M/L] | |
| Heat specific capacity | [E/(MT)] | |
| Coefficients of quadratic failure criteria | [L/F] | |
| Coefficients of quadratic failure criteria | [L/F] | |
| Quantities | Symbols | Units |
| Thicknesses | [L] | |
| Membrane stiffness matrix | [F/L] | |
| Membrane-bending coupling stiffness matrix | [F] | |
| Bending stiffness matrix | [FL] | |
| Out-of-plane shear stiffness matrix | [F/L] | |
| Membrane compliance matrix | [L/F] | |
| Membrane-bending coupling compliance matrix | [1/F] | |
| Bending compliance matrix | [1/(FL)] | |
| Out-of-plane shear compliance matrix | [L/F] | |
| In-plane thermal conductivity matrix | [E/(tT)] | |
| Out-of-plane thermal resistance | [LTt/E] | |
| Surfacic heat capacity | [E/L/T] | |
| In-plane moisture conductivity matrix | [1/t] | |
| Out-of-plane moisture resistance | [Lt] | |
Other units systems can be used with the CLA classes. Each CLA object has an attribute corresponding to the units system in which all its characteristics are defined.
Length: “micron”, “mm”, “cm”, “m”, “mil” (milli-inch), “in”, “ft”.
Mass: “g”, “kg”, “t” (tons), “dat” (deca-tons), “lbm”, “kbm” (kilo-pounds).
Time: “s”, “min”, “hour”.
Force: “N”, “daN”, “kN”, “kgf” (kilogram-force), “lbf” (pound-force), “kips” (kilo-pound-force).
Energy: “J”, “cal”, “BTU”, “ft.lbf”, “in.lbf”, “kgf.m”.
Temperature: “C”, “F”, “K”.
Moisture content: “%w”.
The units of CLA object can be obtained with “getUnits” method that returns a Hash containing pairs of Strings. The first String describes the kind of dimension: “L” for length, “M” for mass, “t” for time, “T” for temperature, “E” for energy, “W” for moisture and “F” for force. The second String corresponds to one of the unit listed above for the selected quantity.
The units of a CLA object can also be modified by calling “setUnits” or “changeUnits” methods:
The “setUnits” method changes the units attributed to an object without modifying the values of the different quantities defining the object. (No unit conversion is done.)
The “changeUnits” method performs the units conversion.
Both “setUnits” and “changeUnits” methods have an Hash argument corresponding to the object returned by “getUnits” method.
When laminate calculations are done, the properties of material used in laminate layup definition are converted in laminate system of units if necessary. The same is true for loading units for the calculation of laminate load response. The ply results (shell forces, shell moments, stresses, temperatures...) are expressed in laminate system of units. When a failure criterion is calculated, calculations are done in laminate system of units. This means that ply allowables are first convered to the laminate system of units. Of course, the use of a consistent system of units for all the composite calculations is recommended, as it reduces the risk of errors and the calculation time.
A ClaDb object may be considered as an object in which collections of materials, laminates and loads are stored. The ClaDb Class also provides the “glue” that bonds the objects of the other composite Classes together.
Table II.2.1 gives the list of methods defined in “ClaDb” class.
The singleton method “new” is used to create ClaDb objects. This method has no argument. (Nor has the “initialize” method an argument.)
Two methods allow the manipulation of the identifier of ClaDb objects (“Id” attribute):
“Id” attribute setter has one argument and sets the identifier. The argument is an identifier (an integer, a String or an Array[int,String]).
“Id” attribute getter has no argument and returns the identifier of the object (same types as above), or nil if no identifier has been attributed to the object.
The ClaDb class provides three methods to insert objects in the collections, and three methods to retrieve objects stored in the collections:
“insertMaterial” makes a copy of the ClaMat argument and inserts it into the materials collection.
“eraseMaterial” removes the specified material from the stored materials collection. The argument is an identifier corresponding to the material to be retrieved.
“‘getMaterialsNbr” returns the number of materials stored in the materials collection.
“getMaterialCopy” returns a copy of a material stored in the materials collection. The argument is an identifier corresponding to the material to be retrieved.
“insertLaminate” makes a copy of the ClaLam argument and inserts it into the laminates collection.
“eraseLaminate” removes the specified laminate from the stored laminates collection. The argument is an identifier corresponding to the laminate to be retrieved.
“‘getLaminatesNbr” returns the number of laminates stored in the laminates collection.
“getLaminateCopy” returns a copy of a ClaLam stored in the laminates collection. The argument is an identifier corresponding to the laminate to be retrieved.
“reInitAllPliesAccelMatrices” re-initializes the ply acceleration matrices of all the laminates stored in the dataBase. (See sections II.4.8.2 and II.1.9.2 for more information.)
“insertLoad” makes a copy of the ClaLoad argument and inserts it into the loads collection.
“eraseLoad” removes the specified load from the stored loads collection. The argument is an identifier corresponding to the load to be retrieved.
“‘getLoadsNbr” returns the number of loads stored in the loads collection.
“getLoadCopy” returns a copy of a ClaLoad object stored in the loads collection. The argument is an identifier corresponding to the load to be retrieved.
The six methods described above create copies of the entities they store to, or retrieve from the ClaDb.
Internally, the ClaDb manages 3 associative containers that associate identifiers to materials, laminates or loads respectively. When an object is stored into the ClaDb, the key which allows to retrieve the object is the identifier one attributed to it with the “Id” attributes. (See Chapters II.3 to II.5.) Note that the identifier used to retrieve an object from the ClaDb must match exactly the key to which the object is associated. For example, if the identifier of a load is [17,"QS_and_bending"], then 17 or "QS_and_bending" will not allow to retrieve a copy of the object. [17,"QS_and_bending"] must be used as argument of the ‘getMaterialCopy” method.
When a ClaLam object is stored into the ClaDb, its properties are calculated automatically. (Stiffness matrix and vector.)
Note also that when a CLA object is extracted from the database, or inserted into the database, the object keeps the units that are attributed to it. These units may be different than the database units. (See also section II.2.4.)
Units are associated to the database, and to all the entities stored in the database. The units associated to the stored entities are independent of each other, and of the database units.
The “ClaDb” class defines several methods for the management of units:
“getDbUnits” returns a Hash containing the definition of units associated to the database.
“setDbUnits” has a Hash argument and sets the units associated to the database. The method does not modify anything else to the CLA entities stored in the database.
“setUnitsAllEntities” has a Hash argument and sets the units associated to the database and all the CLA entities stored in the database.
“setUnitsAllMaterials” has a Hash argument and sets the units associated to all the ClaMat entities stored in the database.
“setUnitsAllLaminates” has a Hash argument and sets the units associated to all the ClaLam entities stored in the database.
“setUnitsAllLoads” has a Hash argument and sets the units associated to all the ClaLoad entities stored in the database.
“changeUnitsAllEntities” has a Hash argument and changes the units associated to the database and all the CLA entities stored in the database.
“changeUnitsAllMaterials” has a Hash argument and changes the units associated to all the ClaMat entities stored in the database.
“changeUnitsAllLaminates” has a Hash argument and changes the units associated to all the ClaLam entities stored in the database.
“changeUnitsAllLoads’ has a Hash argument and changes the units associated to all the ClaLoad entities stored in the database.
The Hash arguments or return values mentioned above have String keys and values as explained in section II.1.13. The difference between the “setUnits” and “changeUnits” methods is also explained in the same section.
Presently, three interface functions are defined:
“readEdf” is used to import the data stored in an ESAComp data file. The function has one argument: a String containing the name of the "edf" file.
When a load is read from an ESAComp file, the reader should keep in mind that the numbering of plies follows different conventions in FeResPost and ESAComp. When a thermo-elastic loading is defined, the ESAComp “bottom” temperature corresponds to FeResPost “Tsup”, and the “top” temperature corresponds to “Tinf”. The same remark applied to thermo-elastic loading.
“readNeutral” is used to import the data stored in a neutral data file. The function has one argument: a String containing the name of the “ndf” file.
“writeNeutral” is used to export the data stored to a neutral data file. The function has one argument: a String containing the name of the “ndf” file.
Note that the neutral data files (“ndf” files) mentioned above are files with a format specific to the FeResPost.
Two methods allow to save or read ClaDb objects from an Array of Strings in neutral format. For each of these two methods, instead of reading or saving the lines from or to a disk file, each line is saved or read from or to an Array of Strings. The two methods are:
“initWithNeutralLines” that initializes the ClaDb object from an Array of Strings interpreted as the content of an NDF file. The argument is the Array of Strings containing the lines.
“getNeutralLines” that returns an Array of Strings corresponding to the lines that would have been written in the NDF file by “writeNeutral” method. This method has no argument.
The ClaDb class provides 6 iterators:
“each_material” iterates on the materials storage and produces pairs of identifier and ClaMat object.
“each_materialId” iterates on the materials storage and produces the identifiers only.
“each_laminate” iterates on the laminates storage and produces pairs of identifier and ClaLam object.
“each_laminateId” iterates on the laminates storage and produces the identifiers only.
“each_load” iterates on the loads storage and produces pairs of identifier and ClaLoad object.
“each_loadId” iterates on the loads storage and produces the identifiers only.
These iterators have no argument.
“clone” method has no argument and returns a copy of the ClaDb object.
The “ClaMat” class is used to store the materials used in the definition of laminates. Each material is characterized by:
An identifier,
A type which can be "isotropic", "orthotropic" or "anisotropic".
Its moduli and Poisson’s coefficients,
Its thermal and moisture expansion coefficients,
Its allowables.
Several methods of the ClaMat class allow to access to data stored in an object. Table II.3.1 gives the list of methods defined in the class.
The singleton method “new” is used to create ClaMat objects. This method has no argument. (Nor has the “initialize” method an argument.)
Two attributes are defined for the “ClaMat” object: “Id” and “Type”. Five methods allow the manipulation of the identifier of material and of its type:
“Id” attribute setter has one argument and sets the identifier. The argument is an identifier (an integer, a String or an Array[int,String]).
“Id” attribute getter has no argument and returns the identifier of the object (same types as above), or nil if no identifier has been attributed to the object.
“Type” attribute setter has one String or integer argument corresponding to the type of the material. Presently, three values are allowed: "isotropic", "orthotropic" or "anisotropic". The type of the object must be set prior to the attribution of material moduli, thermal expansion coefficients and allowables. Note that the attribute “getter” returns an integer.
“TypeName” attribute getter returns a String corresponding to the type (same values as for the “Type” attribute arguments, or "NONE" if no material type is defined).
Note that for the type definition, the integers are 0, 1, 2 or 3 and correspond to "NONE", "isotropic", "orthotropic" or "anisotropic" respectively.
Twelve methods allow to set moduli and Poisson’s coefficients, thermal expansion coefficients and allowables. These methods have one Hash argument that associates String keys to real values.
“clearModuli” has no arguments and erases all the moduli stored in a ClaMat object.
“insertModuli” is used to specify moduli and Poisson coefficients of the material. The keys used to insert mechanical data depend on the type of material:
For an orthotropic material, the different possible keys are: "E1", "E2", "E3", "G12", "G23", "G31", "nu12", "nu23", "nu31".
For isotropic materials the possible keys are "E", "nu" and "G".
For anisotropic materials the components of matrix as defined by (II.1.11) are specified. The keys can be "C1111", "C1122", "C1133"... (Note that when a non-diagonal component of the matrix is defined, its symmetric value is initialized too.)
“fillModuli” is used to set material moduli and Poisson coefficients. This method has the same arguments as “insertModuli” but differs by the fact that moduli and Poisson coefficients are re-initialized before insertion of values.
“clearCTEs” has no arguments and erases all the CTEs stored in a ClaMat object.
“insertCTEs” is used to define different components of the thermal expansion coefficients. For orthotropic and anisotropic materials, possible keys are "alfa1", "alfa2", "alfa3", "alfa12", "alfa23" and "alfa31". For isotropic materials, key "alfa" only can be used.
“fillCTEs” is used to set material CTEs. This method has the same arguments as “insertCTEs” but differs by the fact that CTEs are re-initialized before insertion of values.
“clearCMEs” has no arguments and erases all the CMEs stored in a ClaMat object.
“insertCMEs” is used to define different components of the moisture expansion coefficients. For orthotropic and anisotropic materials, possible keys are "beta1", "beta2", "beta3", "beta12", "beta23" and "beta31". For isotropic materials, key "beta" only can be used.
“fillCMEs” is used to set material CMEs. This method has the same arguments as “insertCMEs” but differs by the fact that CMEs are re-initialized before insertion of values.
“clearAllowables” has no arguments and erases all the allowables stored in a ClaMat object.
“insertAllowables” is used to add material allowables. The possible keys are "sc", "st", "ss", "ec", "et", "gs", "s1c", "s1t", "s2c", "s2t", "s12", "s23", "s31", "e1c", "e1t", "e2c", "e2t", "e3c", "e3t", "g12", "g23", "g31", "F12", "F23" and "F31". "st" is used to calculate isotropic stress criteria or reserve factors. "F12" "F23" and "F31" correspond to the , and of the Tsai-Wu failure criteria (sections II.1.10.14 and II.1.10.15). Note that the "ilss" allowable defined at material level has no effect because for Ilss criterion calculation, the allowable is always extracted from the laminate definition. (More precisely, the ilss laminate allowable, or the ply allowables are used.)
“fillAllowables” is used to set material allowables. This method has the same arguments as “insertAllowables” but differs by the fact that material allowables are re-initialized before insertion of values.
“clearThermalData” has no arguments and erases all the thermal data stored in a ClaMat object.
“insertThermalData” is used to define the thermal data. For orthotropic and anisotropic materials, possible keys are "lambdaT1", "lambdaT2", "lambdaT3", "lambdaT12", "lambdaT23" and "lambdaT31". For isotropic materials, key "lambdaT" only can be used. For all types of materials "rho" and "Cp" keys can be used.
“fillThermalData” is used to set material thermal data. This method has the same arguments as “insertThermalData” but differs by the fact that thermal data are re-initialized before insertion of values.
“clearMoistureData” has no arguments and erases all the Moisture data stored in a ClaMat object.
“insertMoistureData” is used to define the moisture data. For orthotropic and anisotropic materials, possible keys are "lambdaH1", "lambdaH2", "lambdaH3", "lambdaH12", "lambdaH23" and "lambdaH31". For isotropic materials, key "lambdaH" only can be used.
“fillMoistureData” is used to set material Moisture data. This method has the same arguments as “insertMoistureData” but differs by the fact that moisture data are re-initialized before insertion of values.
The type of ClaMat object must have been set prior to the use of any of the three previous methods. (See “Type” attribute described in section II.3.2.) Several methods allow to retrieve the data that define a material:
“getDataModuli” returns the moduli that define the ClaMat object.
“getDataCTEs” returns the CTEs that define the ClaMat object.
“getDataCMEs” returns the CMEs that define the ClaMat object.
“getDataAllowables” returns the allowables that characterize the ClaMat object.
“getThermalData” returns the thermal data that define the ClaMat object.
“getMoistureData” returns the moisture data that define the ClaMat object.
Each of these “get” methods returns a Hash that associates String and Real objects. (See the “fill” corresponding methods for possible values.)
Obviously, the different data inserted in, or retrieved from the ClaMat object should be consistent with the set of units attributed to the same object. This set of units can be attributed to the object after initialization of the data.
Several methods allow to recover stiffness, compliance or conductivity matrices in a specified direction.
“getCompliance” returns an Array of elements corresponding to the material compliance matrix.
“getStiffness” returns an Array of elements corresponding to the material compliance matrix.
“getInPlaneCompliance” returns an Array of elements corresponding to the in-plane material compliance matrix.
“getInPlaneStiffness” returns an Array of elements corresponding to the in-plane material compliance matrix.
“getInPlaneAlfaE” returns an Array of 3 elements corresponding to the in-plane vector.
“getInPlaneBetaE” returns an Array of 3 elements corresponding to the in-plane vector.
“getInPlaneAlfa” returns an Array of 3 elements corresponding to the in-plane vector.
“getInPlaneBeta” returns an Array of 3 elements corresponding to the in-plane vector.
“getOOPSCompliance” returns an Array of elements corresponding to the out-of-plane shear material compliance matrix.
“getOOPSStiffness” returns an Array of elements corresponding to the out-of-plane shear material compliance matrix.
“getOOPSAlfaG” returns an Array of 2 elements corresponding to the out-of-plane vector.
“getOOPSBetaG” returns an Array of 2 elements corresponding to the out-of-plane vector.
“getOOPSAlfa” returns an Array of 2 elements corresponding to the out-of-plane vector.
“getOOPSBeta” returns an Array of 2 elements corresponding to the out-of-plane vector.
“getInPlaneLambdaT” returns an Array of elements corresponding to the in-plane thermal conductivity matrix .
“getInPlaneLambdaH” returns an Array of elements corresponding to the in-plane moisture conductivity matrix .
All these methods have one optional argument: an angle corresponding to the direction of observation wrt material axes, and in which the components of the matrix are expressed.
On the other hand, three methods return material scalar characteristics and have no argument:
“getRho” returns a real value corresponding to the material density .
“getCp” returns a real value corresponding to the material specific heat capacity .
“getRhoCp” returns a real value corresponding to the material volumic heat capacity .
The different calculated results from the ClaMat object are expressed in the units system associated with the object.
The “ClaMat” class defines three methods for the management of units:
“getUnits” returns a Hash containing the definition of units associated to the material.
“setUnits” has a Hash argument and sets the units associated to the material.
“changeUnits” has a Hash argument and changes the units associated to the material.
The Hash arguments or return values mentioned above have String keys and values as explained in section II.1.13. The difference between the “setUnits” and “changeUnits” methods is also explained in the same section.
Two methods allow to save or read ClaMat objects from an Array of Strings in neutral format. These two methods are “initWithNeutralLines” and “getNeutralLines” that work in a similar way as the corresponding methods in “ClaDb” class (section II.2.6).
However, the lines transmitted to “initWithNeutralLines” or returned by “getNeutralLines” correspond to a single ClaMat object definition.
“clone” method has no argument and returns a copy of the ClaMat object.
The “ClaLam” class is used to store lay-ups and calculate laminate mechanical properties and load responses. They are characterized by the lay-up the define.
Table II.4.1 gives the list of methods defined in “ClaLam” class.
One shows in section II.1.6 that two arbitrary parameters and define the relations between and partial derivatives of laminate bending moment components and out-of-plane shear forces when the ” approach is adopted. The default values of these parameters are . Two Class Methods allow the manipulation of these parameters:
“setMuxMuy” has two Real parameters and is used to set the values of and respectively.
“getMuxMuy” returns an Array of two Real objects corresponding to and respectively.
As these methods are Class methods, the modification of or affects all the laminates defined in all the CLA databases.
Similarly, one methods allows to select the laminate out-of-plane shear calculation approach. The method is called “setOopsApproach” and has onesString parameter that has three acceptable values: “Standard”, “UncoupledXY” and “InShearLoadingAxes”. These values correspond to the calculation approaches discussed in section II.1.6.5. “Standard” is the default approach. Method “getOopsApproach” allows to check which approach has been selected. Here again, “setOopsApproach” affects all the laminates defined in all the CLA databases.
“setMuxMuy” and “setOopsApproach” should be used (if used) only once before they creation of the first laminate by FeResPost. Otherwise unexpected behaviour is possible. Indeed, intermediate matrices are stored in C++ laminate objects and the modification of the calculation approach after laminates have been created may lead to mixture of matrices and vectors obtained via different approaches.
The singleton method “new” is used to create ClaLam objects. This method has no argument. Nor has the “initialize” method an argument.)
Two methods allow the manipulation of the identifier of ClaLam objects (“Id” attribute):
“Id” attribute setter has one argument and sets the identifier. The argument is an identifier (an integer, a String or an Array[int,String]).
“Id” attribute getter has no argument and returns the identifier of the object (same types as above), or nil if no identifier has been attributed to the object.
The “clearPlies” method has no argument and erases all the plies defining a ClaLam object. After the method has been called, the number of plies of the laminate is zero.
One way to define the plies of the laminate is to add successively all the plies defined in the laminate starting at the bottom layer. The “addPly” method allows to insert plies in a ClaLam. This method has four or five arguments.
“PlyId” is the global identifier of the ply. This identifier can be an integer, a String or a pair "integer-String" stored in an Array. If one decides not to specify a global ID for the ply, the argument can be omitted (optional argument).
“MatId” is the material id of the ply. This identifier must correspond to an existing material stored in a ClaDb object. The identifier is used internally by the ClaLam class to retrieve material properties and calculate laminate properties.
“Thickness” is a Real argument corresponding to the thickness of the ply. The units must be consistent with those of other data. For example, the thickness may have to be given in meters.
“Angle” is a Real argument corresponding to the orientation of the ply in the laminate. This angle is specified in degrees.
“IlssInf” is the inter-laminar shear stress allowable between the ply being added and the previous ply (lower ply in the layup).
The sequence of plies in the laminate corresponds to the order of addition of the plies by calls to the “addPly” method. Of course each call of the method “addPly” increases the number of plies of the laminate by one.
Instead of defining the sequence of plies sequentially by successive calls to “addPly” method, the data of each ply can also be defined in random order by calls to “setPly” method. Its arguments are nearly the same as those of the “addPly” method:
“Index” is the position in laminate of the ply for which data are defined. It is an integer such that where is the number of plies defined in the Laminate.
“PlyId” (see “addPly” method). This argument is optional.
“MatId” (see “addPly” method).
“Thickness” (see “addPly” method).
“Angle” (see “addPly” method).
“IlssInf” (see “addPly” method).
As the “PlyId” second argument is optional, the method has 5 or 6 arguments. The “setPly” method is very handy when one defines a new laminate by modifying a few plies from a previously existing one. Of course, an entirely new laminate can also have its ply data initialized with “setPly” method, but then the number of plies must first be set... “setNbrPlies” method has one argument and sets the number of plies. Note that the ply definition data previously stored in the laminate may have random values after using this method.
Two methods allow to access and examine the plies stored in a ClaLam object:
“getNbrPlies” has no argument and returns the number of plies.
“getPlyData” returns the data for one specific ply. The method has one argument: the local index of the ply in the laminate (its position in the lay-up). if the laminate has plies, then the index must be . (The first ply has index 0.)
The method returns an Array containing 5 elements corresponding to the arguments of the “addPly” method.
Obviously, the different data inserted in, or retrieved from the ClaLam object should be consistent with the set of units attributed to the same object. This set of units can be attributed to the object after initialization of the data.
The reference temperature of a laminate is accessed with the two following methods:
“clearAllowables” has no arguments and erases all the allowables stored in a ClaLam.
“insertAllowables” is used to add material allowables. This method must be used if the calculation of failure indices or reserve factor is done using laminate allowables instead of ply materials allowables. (See section II.3.3 for more explanation on the use of this method.)
“getDataAllowables” has no arguments and returns a Hash containing the data defining allowables. (See the corresponding method in ClaMat class section II.3.3.)
“setRefT” has one Real argument and sets the reference temperature of the laminate.
“getRefT” returns the reference temperature (a Real object).
“setRefH” has one Real argument and sets the reference moisture of the laminate.
“setLaminateIlss” has one Real argument and sets the value of laminate inter-laminar shear strength allowable at laminate level.
“setAllPliesIlss” has one Real argument and sets the value of laminate inter-laminar shear strength allowable for all the plies defined in the ClaLam.
Note that an ILSS criterion is calculated, the allowables are always extracted from the laminate definition. When no ClaDb argument is provided for the calculation of the criterion, the laminate “ilss” allowable is used; when a ClaDb argument is provided, the ply “ilss” allowables are used. This means that the “ilss” allowable provided in ClaMat materials is never used.
Obviously, the different data inserted in, or retrieved from the ClaLam object should be consistent with the set of units attributed to the same object. This set of units can be attributed to the object after initialization of the data.
The method “calcLaminateProperties” calculates the laminate properties of the ClaLam object. This means that the stiffness and compliance matrices, the thermal-expansion vectors are estimated and stored into the laminate object. This method can be called only after all the plies of the laminate have been inserted into the object. The method has one argument: a ClaDb object in which all the materials used in the lay-up definition have to be stored (otherwise, an exception is raised). Note that when a ClaLam object is inserted into a ClaDb, the “calcLaminateProperties” method is called automatically, with this ClaDb object as argument.
Six methods allow to retrieve the properties of a laminate:
“get_ABBD” returns the ABBD stiffness matrix. More precisely, the object returned by this method is an Array of 6 elements. Each element corresponds to one line of the matrix and is an Array of 6 Real objects.
“get_G” returns the out-of-plane shear stiffness matrix. More precisely, the object returned by this method is an Array of 2 elements. Each element corresponds to one line of the matrix and is an Array of 2 Real objects.
“get_alfaEh1”, “get_alfaEh2” and‘ ‘get_alfaEh3” return 3-components vectors , and as defined by equations (II.1.56), (II.1.57) and (II.1.58) respectively.
“get_alfaGh1” and “get_alfaGh2” return 2-components vectors and as defined by equations (II.1.66) and (II.1.67) respectively.
“get_betaEh1”, “get_betaEh2” and “get_betaEh3” return 3-components vectors , and as defined by equations (II.1.71), (II.1.72) and (II.1.73) respectively.
“get_betaGh1” and “get_betaGh2” return 2-components vectors and as defined by equations (II.1.80) and (II.1.81) respectively.
“get_abbd_complMat” returns the abbd compliance matrix. (Format similar as “get_ABBD”.)
“get_g_complMat” returns the out-of-plane shear compliance matrix. More precisely, the object returned by this method is an Array of 2 elements. Each element corresponds to one line of the matrix and is an Array of 2 Real objects.
“get_alfae0”, “get_alfae1”, “get_alfak0” and “get_alfak1” return 3-components Array containing the components of laminate CTE vectors , , and as defined by expressions (II.1.61), (II.1.62), (II.1.63) and (II.1.64).
“get_alfas0” and “get_alfas1” return 2-components Arrays containing the components of laminate CTE vectors and defined by expressions (II.1.69) and (II.1.70).
“get_betae0”, “get_betae1”, “get_betak0” and “get_betak1” return 3-components Array containing the components of laminate CTE vectors , , and as defined by expressions (II.1.75), (II.1.76), (II.1.77) and (II.1.78).
“get_betas0” and “get_betas1” return 2-components Arrays containing the components of laminate CTE vectors and defined by expressions (II.1.82) and (II.1.83).
“get_engineering” returns a Hash containing equivalent engineering constants of the laminate. More precisely in-plane moduli and Poisson coefficients are returned for in-plane loading, in-plane with curvature constrained to zero, and pure flexion of the laminate. Each element of the Hash is a pair String-Real. The different values of the Strings are: "E_xx", "E_yy", "G_xy", "nu_xy", "nu_yx", "E_k0_xx", "E_k0_yy", "G_k0_xy", "nu_k0_xy", "nu_k0_yx", "E_f_xx", "E_f_yy", "G_f_xy", "nu_f_xy", "nu_f_yx", "G_xz", "G_yz".
“get_LambdaT” returns the in-plane thermal conductance matrix .
“get_LambdaH” returns the in-plane moisture conductance matrix .
These five methods have one optional Real argument that corresponds to a rotation angle wrt laminate axes. If the argument is omitted, zero value is assumed and the engineering constants are calculated in laminate axes. The angle is specified in .
Four methods return Real scalar values:
“get_thickness” returns the total thickness of the laminate .
“get_surfacicMass” returns the surfacic mass of the laminate .
“get_averageDensity” returns the average density of the laminate .
“get_R33T” returns the out-of-plane thermal conductance of the laminate .
“get_RhoCpH” returns the thermal surfacic capacity of the laminate .
“get_R33H” returns the out-of-plane moisture conductance of the laminate .
These methods have no arguments.
The different calculated results from the ClaLam object are expressed in the units system associated with the object.
The calculation of the laminate response to a specified loading is always done in two steps:
The laminate load response is calculated for a specific loading. This calculation is used to estimate laminate in-plane forces, bending moments, average strains, curvature, temperature variations... Also layered results are calculated if required. (See description of method “calcResponse” in section II.4.7.1.)
All these results are stored in the ClaLam object and remembered until the next calculation is performed.
Then, the laminate can be “interrogated” to obtain a restitution of stored results, or the calculation of new results from the information stored since the last calculation. (See the methods described in sections II.4.7.2, II.4.7.3 and II.4.7.5.)
This way of working allows at the same time much flexibility in the recovery of results at an acceptable computational cost.
The different calculated results retrieved from the ClaLam object are expressed in the units system associated to laminate object. This means that even if the loading units or the material units differ from laminate units, FeResPost performs the conversions needed to obtain stresses, forces, moments and other results in the units system associated to laminate.
The method “calcResponse” is used to calculate the laminate response to a specified loading. When this method is called, several results are systematically calculated and stored: in-plane forces, bending moments, average strains, curvature and temperature variation. The calculation and storage of ply results is optional and commanded by the Boolean arguments of the method.
The “calcResponse” may have from 3 up to 6 arguments:
A ClaDb object. This object is necessary, because information about the material properties of the different plies may be necessary to perform the calculation.
A real value corresponding to the orientation of loading wrt laminate axes. The angle is given in degrees.
A ClaLoad object containing the loading definition. (See Chapter II.5 for the description of loads.)
A logical parameter specifying whether the stresses and strains are to be calculated at the bottom of each laminate ply.
A logical parameter specifying whether the stresses and strains are to be calculated at mid thickness of each laminate ply.
A logical parameter specifying whether the stresses and strains are to be calculated at the top of each laminate ply.
The three last parameters are optional and default to false (no calculation of the corresponding layered results).
Several methods allow to recover results calculated at laminate level. All these results correspond to the laminate results for the last call to method “calcResponse”:
“isThermalLoadingDefined” returns a logical that specifies whether the last load response calculation has been calculated with a thermo-elastic contribution.
“getDeltaT” returns a Real values corresponding to the difference between the load average temperature and the reference temperature of the laminate.
“getT0” returns a Real values corresponding to the average temperature used in the last load response.
“getGradT” returns a Real values corresponding to the temperature out-of-plane gradient used in the last load response.
“isMoistureLoadingDefined” returns a logical that specifies whether the last load response calculation has been calculated with a hygro-elastic contribution.
“getDeltaH” returns a Real values corresponding to the difference between the load average moisture and the reference moisture of the laminate.
“getH0” returns a Real values corresponding to the average moisture used in the last load response.
“getGradH” returns a Real values corresponding to the moisture out-of-plane gradient used in the last load response.
“isMechanicaLoadingDefined” returns a logical that specifies whether the laminate contain a load response. (When a laminate load response is calculated, a mechanical contribution to the loading is mandatory.)
“getNormalForces” returns the in-plane normal forces in an Array of three Real values. This method has one optional argument corresponding to a rotation wrt laminate axes.
“getMoments” returns the bending moments in an Array of three Real values. This method has one optional argument corresponding to a rotation wrt laminate axes.
“getShearForces” returns the out-of-plane shear forces in an Array of two Real values. This method has one optional argument corresponding to a rotation wrt laminate axes.
“getNormalStrains” returns the in-plane average strains in an Array of three Real values. This method has one optional argument corresponding to a rotation wrt laminate axes.
“getCurvatures” returns the curvature tensor in an Array of three Real values. This method has one optional argument corresponding to a rotation wrt laminate axes.
“getShearStrains” returns the average out-of-plane shear strains in an Array of two Real values. This method has one optional argument corresponding to a rotation wrt laminate axes.
“getAverageInPlaneStresses” returns the average in-plane stress tensor components in an Array of three Real values. This method has one optional argument corresponding to a rotation wrt laminate axes.
“getFlexuralStresses” returns the top surface stress tensor components corresponding to bending moment assuming homogenous material. The components are returned in an Array of three Real values. This method has one optional argument corresponding to a rotation wrt laminate axes.
“getAverageShearStresses” returns the average out-of-plane shear stress tensor components in an Array of two Real values. This method has one optional argument corresponding to a rotation wrt laminate axes.
“getAverageInPlaneStrains” returns the in-plane average strain tensor components in an Array of three Real values. This method has one optional argument corresponding to a rotation wrt laminate axes.
“getFlexuralStrains” returns the top surface strain tensor components corresponding to bending moment. The components are returned in an Array of three Real values. This method has one optional argument corresponding to a rotation wrt laminate axes.
“getAverageShearStrains” returns the out-of-plane shear components of average strain tensor in an Array of three Real values. This method has one optional argument corresponding to a rotation wrt laminate axes.
The optional rotation is specified as an angle expressed in degrees. When the parameter is omitted, a zero value is assumed. When a tensor is returned the three components are given in the following order: XX, YY and XY.
Three methods give access to the ply results stored in ClaLam object:
“getPliesStrains” returns the components of the strain tensor stored in the layered results of the laminate.
“getPliesStresses” returns the components of the stress tensor stored in the layered results of the laminate.
“getPliesMechanicalStrains” returns the components of the Mechanical Strain Tensor stored in the layered results of the laminate according to (II.1.18). This tensor corresponds to the “Mechanical Strain Tensor” presented in Tables X.C.3 and III.2.4.
These three methods:
Have an arbitrary number of arguments. Each argument corresponds to an identifier of the layer and location at which the layered components are recovered. The identifier is given as an Array of two elements: the ply local integer index and an String that can have "Inf", "Mid" or "Sup" value. Among these layers, only those for which layered components have been previously calculated and stored are returned by the method. If the call is done without argument, all the layered results stored in the laminate are returned.
They return components expressed in the ply coordinate system.
The components are calculated assuming that .
The components are returned by the method only if their calculation and storage has been required in the last call to “calcResponse”. (See section II.4.7.1.)
The methods return an Array of which each element corresponds to the stresses/strains at one given location in the thickness of the laminate. More precisely, each element is an Array of 2+6=8 elements containing:
The two first elements identify the layer: they correspond to the integer index of the ply between 0 and , and the String location in the ply ("Inf", "Mid" or "Sup"). (Note that this does not correspond to the ply identifier. The integer index corresponds to the position of the ply in laminate lay-up.)
The next 6 real elements contain the components of the result in the following order: 11, 22, 33, 23, 13, 12.
To the three methods listed above correspond three other methods that return the ply stresses or strains with components expressed in a coordinate system defined wrt the laminate, and not expressed in ply axes. The three methods are called:
The first argument of these three methods are a real value corresponding to the rotation of restitution coordinate system wrt laminate axes. The following arguments are the same as those of the three first methods defined above.
Four methods give access to the temperature and moisture ply results stored in ClaLam object:
“getPliesDeltaT” returns the variation of temperature in plies.
“getPliesDeltaH” returns the variation of moisture in plies.
The arguments are the same as those of the method described in section II.4.7.3: they correspond to the identifiers of layers at which ply results are recovered. The methods return an Array of which each element corresponds to a layered Result. More precisely, each element is an Array of 3 elements containing:
The two first elements identify the layer: they correspond to the integer index of the ply between 0 and , and the String location in the ply ("Inf", "Mid" or "Sup").
The third element is a Real value containing the corresponding returned value.
Several methods of the ClaLam class allow to estimate values from the stored ply stresses and strains. Three such methods return the values calculated for several plies:
“getDerived” returns an equivalent stress or strain corresponding to the components stored in the laminate. For example, a Tresca or Von Mises equivalent stress.
“getFailureIndices” is devoted to the calculation of failure indices like the Tsai-Hill or Tsai-Wu. This method differs from the previous one by the fact that failure indices are calculated from the stored results and corresponding allowables.
“getDerived” and “getFailureIndices” have the same parameters:
A ClaDb object that provides the definition of materials used in the laminate, and of the corresponding allowables. If this first parameter is omitted, then the allowables stored in ClaLam object are used instead of material allowables.
An Array of Strings containing a list of criteria for the calculations.
Then follows an arbitrary number of arguments. Each argument corresponds to an identifier of the layer and location at which the layered components are recovered. (Same principle as methods returning plies strains and strains in section II.4.7.3.) If none of these arguments identifier is provided, the calculation is done for all layers.
So for example, “getFailureIndices” method may be called as follows:
criteria=["TsaiHill2D","MaxStress2D"] ... fiRes=getFailureIndices(criteria) ... fiRes=getFailureIndices(db,criteria) ... fiRes=getFailureIndices(db,criteria,[4,"Sup"],[7,"Inf"])
Note that several criteria can be calculated by a single call.
Methods “getReserveFactors” and “getStrengthRatios” have one additional parameter: the factor of safety. This parameters is a Real value provided after the list of criteria and before the optional layer identifiers. For example
criteria=["TsaiHill2D","MaxStress2D"] ... rfRes=getReserveFactors(db,criteria,1.25,[4,"Sup"],[7,"Inf"])
Each of the four methods described above returns an Array containing two elements:
The first element is an Array of Strings containing the list of criteria that have been calculated. Indeed, the criteria are calculated only if the criterion is available. This Array has X elements.
The second element contains the new layered results. Each element of this Array contains 2+X elements:
The two first elements of the sub-array identify the layer to which the calculated results correspond.
The X elements 3 to 2+X of the sub-array contain the Real calculated values. These X elements correspond to the X Strings referred to above in the list of criteria returned by the method.
The four methods “getDerived”, “getFailureIndices”, “getReserveFactors” and “getStrengthRatios” have “Min” and “Max” variants. This makes six additional methods: “getMinDerived”, “getMinFailureIndices”, “getMinReserveFactors”, “getMinStrengthRatios”, “getMaxDerived”, “getMaxFailureIndices”, “getMaxReserveFactors” and “getMaxStrengthRatios”. These methods have the same parameters as their basic corresponding methods and are used to return values associated to the most critical ply. (The ply leading to maximum or minimum calculated criterion.) The returned Array, however, is different. The returned value is an Array of which each element is an Array of four elements:
The calculated criterion (String).
Two elements identifying the critical layer (an integer and string value).
A Real object corresponding to the critical value.
The criteria presently available are summarized in Table II.1.2.
The “calcFiniteElementResponse” method allows the calculation of finite element load response. More precisely the method calculates several Result objects containing finite laminate finite element results, from loading of which some components are finite element results. The method has up to nine arguments:
The first argument is a “ClaDb” object in which the materials used in the laminate definition are stored.
The second argument, “theta”, is a real value corresponding to the angle in degrees of loading wrt laminate axes. In most cases, this angle will be zero. Note that the same angle is used to calculate laminate load response for all elements and nodes on which it is required.
The third argument is a ClaLoad object in which the loading is defined. This ClaLoad object must have some components defined as finite element results.
The fourth argument is an Array of three logical values. Each logical value corresponds to the request of results at bottom, mid and top location respectively, in each ply. (The components are similar to three of the arguments of “calcResponse” method described in section II.4.7.1.)
The fifth parameter is an Array of Strings specifying the non-layered laminate results that will be returned by the method.
The sixth parameter is an Array of Strings specifying the layered laminate results that will be returned by the method. (Results at ply level.)
The seventh parameter is a Real object corresponding to the safety factor. This parameter is used by the method only for the calculation of reserve factors, or strength ratios. (See the following argument.)
The eighth parameter is an Array of Arrays describing the failure indices, reserve factors or equivalent scalar derived values requirements. Each element of the first Array is an Array of up to five elements:
A String corresponding to the key by which the corresponding result shall be referred in the Hash returned by “calcFiniteElementResponse” method.
A String corresponding to the name of the criterion. This name must one of the names defined in Table II.1.2.
A string defining the type of Result that shall be defined. Values can be “FI”, “RF”, “SR” or “EQ”. They correspond to the calculation of Failure Indices, Reserve Factors, Strength Ratios or Scalar Derived values respectively. If a Reserve Factor or Strength Ratio is required, the factor of safety parameter is used for the calculation.
A logical value specifying whether the laminate allowables are used for the calculation of Result values. If this value is false, then the ply material allowables are used in the calculations.
A logical value specifying if Result values are required for all the plies. If the argument is “false”, the critical layer value only is inserted in the returned Result.
The Logical parameters are optional. If not defined, “false” values are assumed.
An Array containing the list of plies on which stresses, strains or scalar failure indices are to be calculated. (For example, an Array of integers corresponding to ply idfiers.)
The method returns a Hash object containing pairs of Strings and Results. One can make a few remarks that should help to understand Results returned by the method:
FeResPost first calculates a list of all the entities (elements, or elements and their corner nodes) for which mechanical, thermo-elastic or hygro-elastic loading components are defined in the ClaLoad object. FeResPost calculates a load response and corresponding finite element Results for all these finite element entities.
When mechanical loading components are defined as finite element Results, it is the responsibility of the user to first transform the components in such a way that their use by FeResPost makes sense. This means that the Results must be expressed in the appropriate coordinate system. (See also section II.5.6.)
When mechanical loading components are defined as finite element Results, and when for some components, and if some of the finite element entities (elements or nodes) are not present in all the corresponding finite element Result stored in the ClaLoad object, FeResPost assumes the corresponding components to be zero for the loading of the entity.
When thermo-elastic or hygro-elastic components are defined as finite element Results:
Values on upper and lower faces correspond to the finite element temperatures found at layers Z1 and Z2 respectively.
If values at Z1 and/or Z2 are not found, and a value is found at layer Z0 or NONE, this value is used instead. Note that when both Z0 and NONE layers are found in the layers, Z0 layer value supersedes the NONE layer value.
If either of the two values at Z1 or Z2 is not found by either of the two methods listed above, then the thermo-elastic or hygro-elastic contribution is not considered for laminate response analysis of the current FEM entity.
Non-layered vectorial or tensorial Results are calculated in laminate axes. Layered vectorial and tensorial Results are calculated in ply axes. Scalar Results are not associated to a coordinate system.
The “Ilss” and “Ilss_b” scalar results are always calculated at bottom layer of each ply, even if no explicit request of output to bottom sub-layer has been done.
The requirements for laminate non-layered and layered Results are summarized in Table II.4.2 and Table II.4.3 respectively.
An example of use of the method follows:
criteria = [] criteria << ["TS FI","TsaiHill2D","FI",true,true] criteria << ["TW FI","TsaiWu2D","FI",true,true] criteria << ["TW FI Critical","TsaiWu2D","FI",true,false] criteria << ["ILSS FI Critical","Ilss","FI",true,false] theta=0.0 outputs=lam.calcFiniteElementResponse(compDb,theta,ld,[true,true,true], ["Shell Forces","Shell Moments", "Shell Curvatures", "Average Strain Tensor"], ["Stress Tensor","Strain Tensor","Mechanical Strain Tensor", "Ply Temperature Variation"], 1.5,criteria)
| Requirement | Finite Element Result |
| “Shell Forces” | “Shell Forces” |
| “Shell Moments” | “Shell Moments” |
| “Shell Curvatures” | “Shell Curvatures” |
| “Average Strain Tensor” | “Average Strain Tensor” |
| Requirement | Finite Element Result |
| “Stress Tensor” | “Stress Tensor” |
| “Strain Tensor” | “Strain Tensor” |
| “Mechanical Strain Tensor” | “Mechanical Strain Tensor” |
| “Ply Temperature” | “Ply Temperature” |
| “Ply Temperature Variation” | “Ply Temperature Variation” |
| “Ply Moisture” | “Ply Moisture” |
| “Ply Moisture Variation” | “Ply Moisture Variation” |
Note that the same method with exactly the same arguments has been defined in the DataBase class. (See section I.1.5.)
The different calculated results from the ClaLam object are expressed in the units system associated with the object.
One explains in section II.1.9.2 how the plies stresses and strains calculation can be significantly accelerated by calculating once and for all intermediate acceleration matrices for each ply. These matrices must be recalculated each time the laminate or one of its materials is modified.
Method “reInitAllPliesAccelMatrices” has been added to the “ClaLam” class to re-initialize the laminate plies acceleration matrices. This ensures that the matrices will be re-calculated next time they are required.
The “calcFiniteElementCriteria” method allows the calculation of ply failure criteria, reserve factors or equivalent stress or strain from layered Results. The method has four arguments:
“ClaDB” a ClaDb object from which ply allowables and needed for the calculations are retrieved.
“InRes” a tensorial Result object corresponding to “Stress Tensor”, “Strain Tensor” or “Mechanical Strain Tensor” the components of which are used to estimate the criteria. It is the responsibility of the user to provide the tensor corresponding to the requested criteria.
“FoS” a Real object corresponding to the factor of safety.
“FiRfResReq” the requested criteria outputs. (See the description of method “calcFiniteElementResponse” for a detailed description of the argument.)
The method returns a Hash object containing pairs of Strings and Results. In this case, only scalar Result objects are returned.
The different calculated results from the ClaLam object are expressed in the units system associated with the object.
The “ClaLam” class defines three methods for the management of units:
“getUnits” returns a Hash containing the definition of units associated to the laminate.
“setUnits” has a Hash argument and sets the units associated to the laminate.
“changeUnits” has a Hash argument and changes the units associated to the laminate.
The Hash arguments or return values mentioned above have String keys and values as explained in section II.1.13. The difference between the “setUnits” and “changeUnits” methods is also explained in the same section.
Two methods allow to save or read ClaLam objects from an Array of Strings in neutral format. These two methods are “initWithNeutralLines” and “getNeutralLines” that work in a similar way as the corresponding methods in “ClaDb” class (section II.2.6).
However, the lines transmitted to “initWithNeutralLines” or returned by “getNeutralLines” correspond to a single ClaLam object definition.
The ClaLam class provides the iterator “each_ply” that iterates on the plies. This iterator returns pairs of elements corresponding to the ply index, and the ply definition. The ply definition is an Array of 5 elements identical to the one returned by “getPlyData” method.
“clone” method has no argument and returns a copy of the ClaLam object.
The “ClaLoad” class is used to define, store and manipulate loadings to be applied to laminates. A loading is characterized by:
The thermo-elastic loading of the laminate defined by a specified temperature.
The membrane part of mechanical loading. Three such components , and are given.
The flexural part of mechanical loading. Three such components , and are given.
The out-of-plane shear part of mechanical loading. Two such components and are given.
The types of solicitation for each component of the mechanical loading. This type is specified separately for each component of the mechanical loading. This means that three components are specified for the membrane part, three components for the flexural part and two components for the out-of-plane shear part. For each component, the type of solicitation can be:
“FM” means that a normal force are specified for a membrane component (expressed for example in N/m), a bending moments for a flexural component (in Nm/m) and again a force per unit of length for out-of-plane shear (in N/m). “femFM” has the same meaning as “FM” but specifies that the load components shall be extracted from the finite element results stored in the ClaLoad object when calculating laminate load response (“Shell Forces” or “Shell Moments”).
“SC” Means that strains are specified for membrane components (in m/m), curvature for flexural components (in 1/m), and again average shear strain for the out-of-plane shear components. Note that the shear components are given as angular components . Also the component of curvature tensor is a kind of angular component as defined by equation. “femSC” has the same meaning as “SC” but specifies that the load components shall be extracted from the finite element results stored in the ClaLoad object when calculating laminate load response (“Shell Strains” or “Shell Curvatures”, see equation II.1.32).
“NS” means that normalized stress is specified for the component whatever the part of the loading is concerned.
The default values of loading are of the type “FM” with zero components. This means zero normal forces, zero bending moments, and zero out-of-plane shear forces. When the laminate load response is calculated, moisture and temperature load contributions are taken into account only if they have been initialized in the ClaLoad object.
For thermo-elastic and hygrometric parts of loading, it is also possible to specify a loading with finite element results. The type of loading is determined by the value of String first argument of “setT” and “setH” methods which can be “fem” or “noFem”.
A list of the methods defined in “ClaLoad” class is given in Table II.5.1.
The singleton method “new” is used to create ClaLoad objects. This method has no argument. (Nor has the “initialize” method an argument.)
Two methods allow the manipulation of the identifier of ClaLoad objects (“Id” attribute):
“Id” attribute setter has one argument and sets the identifier. The argument is an identifier (an integer, a String or an Array[int,String]).
“Id” attribute getter has no argument and returns the identifier of the object (same types as above), or nil if no identifier has been attributed to the object.
Ten methods allow the manipulation of scalar characteristics of the loadings. (The scalar characteristics are the thermo-elastic and hygro-elastic contributions to loading.) The methods are:
“setT” is used to set thermo-elastic part of loading. The method has two or three arguments:
The first argument is a String specifying whether the laminate load response shall use the finite element Result temperatures to calculate load response, or the two constant values provided as arguments 2 and/or 3. (This argument is “fem” or “noFem”.)
The second and/or third argument(s) are the laminate bottom and top temperatures. These arguments are Real values. If only one temperature is provided, the bottom and top laminate temperatures are initialized to the same value.
“getTinf” returns a Real value corresponding to the bottom temperature.
“getTsup” returns a Real value corresponding to the top temperature.
“isTdefined” returns true if a temperature contribution has been defined in the ClaLoad, and returns false otherwise.
“unsetT” erases the temperature contribution defined in the ClaLoad object.
“setH” is used to set hygro-elastic part of loading. The method has two or three arguments:
The first argument is a String specifying whether the laminate load response shall use the finite element Result moistures to calculate load response, or the two constant values provided as arguments 2 and/or 3. (This argument is “fem” or “noFem”.)
The second and/or third argument(s) are the laminate bottom and top moistures. These arguments are Real values. If only one moisture is provided, the bottom and top laminate moistures are initialized to the same value.
“getHinf” This function returns a Real value corresponding to the bottom moisture.
“getHsup” This function returns a Real value corresponding to the top moisture.
“isHdefined” returns true if a moisture contribution has been defined in the ClaLoad, and returns false otherwise.
“unsetH” erases the moisture contribution defined in the ClaLoad object.
Obviously, the different data inserted in, or retrieved from the ClaLoad object should be consistent with the set of units attributed to the same object. This set of units can be attributed to the object after initialization of the data.
Three methods are used to set the mechanical part of loading stored in the ClaLoad object:
“setMembrane” sets the membrane part of the loading. The method has from 1 up to 4 arguments. The first argument is an Array of three Real values corresponding to the components of loading , and given in loading axes. The five following optional arguments are Strings giving the type of solicitation of the corresponding components. The possible values of these types of solicitations are "FM", "femFM", "SC", "femSC", and "NS". (See an explanation page 511.) If optional arguments are omitted, the default value "FM" is assumed.
The “fem” versions of component loading types specify that when laminate load response shall be calculated, the corresponding component shall be retrieved from the finite element results stored in the ClaLoad object.
“setFlexural” sets the flexural part of the loading. The method has the same argument types as method “setMembrane”.
“setOutOfPlane” sets the out-of-plane shear part of the loading. The method has from 1 up to 3 arguments. The first argument is an Array of two Real values corresponding to the components of out-of-plane shear: and . The two optional arguments are Strings corresponding to the type of solicitation of the components.
Each of the three “set” methods described above has a corresponding “get” method:
Each of these three “get” methods returns an Array containing the arguments of the respective “set” methods. The first element of this Array is an Array of 3 or 2 Real values. Then follow 3 or 2 Strings corresponding to the types of solicitation of each component.
Obviously, the different data inserted in, or retrieved from the ClaLoad object should be consistent with the set of units attributed to the same object. This set of units can be attributed to the object after initialization of the data.
“setToCombili” method allows to define a ClaLoad as a linear combination of pre-defined ClaLoads. This method has four arguments:
A reference temperature. This Real parameter is necessary because the top and bottom temperatures of the combined ClaLoad are calculated as follows:
|
|
A reference moisture. (Same remarks as for the reference temperature.)
An Array of Reals corresponding to the coefficients of the linear combination.
An Array of ClaLoad objects.
The sizes of the two Array arguments must match. Also the types of the different components of mechanical part of the loadings must be the same.
Eighteen methods are devoted to the manipulation of loading components defined as finite element Results. Six member data correspond to these methods: “Shell Forces”, “Shell Moments”, “Shell Strains”, “Shell Curvatures”, “Shell Temperatures” and “Shell Moistures”.
The mechanical components of loading correspond to non-layered Results. “Shell Temperatures” and “Shell Moistures” are defined at Shell lower and upper surfaces (layers “Z1” and “Z2” respectively). When calculating laminate load response, FeResPost does not check or considers the coordinate system to which mechanical loading components are associated. This means that all the components are assumed to be given in loading axes. It is the responsibility of the user to first transform the components in such a way that their use by FeResPost makes sense.
Three methods allow the manipulation of Shell Forces stored in the ClaLoad object:
“setShellForces” inserts a copy of the Result argument inside the ClaLoad object.
“getShellForcesCopy” has no argument and returns a copy of the “Shell Forces” Result stored in the ClaLoad object. The method returns “Nil” if the “Shell Forces” are not initialized.
“clearShellForces” erases the “Shell Forces” Result stored in the ClaLoad object.
For the other Results, the manipulation methods are build similarly. The other methods are:
“setShellMoments”, “getShellMomentsCopy” and “clearShellMoments” for the manipulation of “Shell Moments”.
“setShellStrains”, “getShellStrainsCopy” and “clearShellStrains” for the manipulation of “Shell Strains”.
“setShellCurvatures”, “getShellCurvaturesCopy” and “clearShellCurvatures” for the manipulation of “Shell Curvatures”.
“setShellTemperatures”, “getShellTemperaturesCopy” and “clearShellTemperatures” for the manipulation of “Shell Temperatures”.
“setShellMoistures”, “getShellMoisturesCopy” and “clearShellMoistures” for the manipulation of “Shell Moistures”.
Obviously, the different data inserted in, or retrieved from the ClaMat object should be consistent with the set of units attributed to the same object. This set of units can be attributed to the object after initialization of the data.
The “ClaLoad” class defines three methods for the management of units:
“getUnits” returns a Hash containing the definition of units associated to the load.
“setUnits” has a Hash argument and sets the units associated to the loads.
“changeUnits” has a Hash argument and changes the units associated to the loads.
The Hash arguments or return values mentioned above have String keys and values as explained in section II.1.13. The difference between the “setUnits” and “changeUnits” methods is also explained in the same section.
Two methods allow to save or read ClaLoad objects from an Array of Strings in neutral format. These two methods are “initWithNeutralLines” and “getNeutralLines” that work in a similar way as the corresponding methods in “ClaDb” class (section II.2.6).
However, the lines transmitted to “initWithNeutralLines” or returned by “getNeutralLines” correspond to a single ClaLoad object definition.
“clone” method has no argument and returns a copy of the ClaLoad object.
In this Part of the document, one describes the preferences for the different solvers supported by FeResPost. Most preferences are defined as methods and member data of the classes specializing the “DataBase” class defined Chapter I.1. Presently two solvers are supported: Nastran and Samcef. The corresponding classes specializing “DataBase” class are “NastranDb” and “SamcefDb” classes. The corresponding preferences are described in Chapters III.1 and III.2 respectively. The diagram of Figure I.1.1 representing the “DataBase” hierarchy can be more precisely represented as in Figure 1.
Most methods peculiar to the post-processing of Nastran finite element Results and models are defined in class “NastranDb” that inherits the “DataBase” class. This class is described in section III.1.1. A list of the methods defined in “NastranDb” class is given in Table III.1.1.
A “NastranDb” object can be created by a statement using “new” method like:
db=NastranDb.new()
Method “initialize” initializes or clears a NastranDb object. This class is a specialization of the FeResPost “DataBase” class.
The model can be defined by reading a bulk Data File, or an op2 file. (See the corresponding methods below.)
The finite element model can be imported from a Nastran Bulk Data File with method “readBdf”. The method has up to six arguments.
A String containing the name of the main Nastran Bulk Data File.
An Array of Strings containing the list of directories in which files specified by “include” statements shall be searched. Its default value is a void Array.
The name of an extension that may be added to the file names specified in include statements. Its default value is a void String. (This argument corresponds to the jidtype in Nastran.)
A Hash with String keys and values corresponding to the list of “symbols” that can be used in “include” statements in the Bulk Data Files. The default value is a void Hash.
A Logical that specifies verbosity for the reading of the Nastran Bulk Data File. Its default value is “false”. This parameter is redundant with “setVerbosityLevel” of “Post” Module: to set the parameter to “true” is equivalent to set “Post” verbosity level to 1.
A Logical that specifies whether the file contains only Bulk Data Section lines. Its default value is “false”. If the parameter is “true”, the “BEGIN BULK” and “ENDDATA” lines are ignored, and all the input lines, except comments, are interpreted. (See also the remarks below.)
Only the first argument of the method is mandatory. More information about the method is given in section III.1.1.1. Examples of valid “readBdf” statements follow:
db.readBdf("../../MODEL/MAINS/unit_xyz.bdf",
[],"",{},true)
db.readBdf("Z:/RD/ALCAS/TESTSAT/MODEL/MAINS/unit_xyz.bdf",
[],"",{},true)
db.readBdf("//CALC01/TESTSAT/MODEL/MAINS/unit_xyz.bdf",
[],"",{},true)
db.readBdf("//CALC01/TESTSAT/MODEL/MAINS/unit_xyz.bdf",
[],"",{},true,true)
The format of Nastran cards defined in a bulk data file is described in [Sof04b]. The user must take the following limitations of the interface into account:
Only ASCII characters should appear in the path specifying the BDF file. The path to BDF file should contain no special character like accentuated letters (“é”, “è”, “î”, “ò”, “ù”...) or other “strange” characters corresponding to other languages (Polish, Greek, Russian, Chinese, Arabic...). This rule is also valid for the sub-files read via an include statement.
Actually, this is more a recommendation that a rule because on some platforms, special characters seem to be supported. Tests have demonstrated good performance on LINUX system, but Failure of BDF reading on Windows when path to file contains special characters.
Generally, only the lines between “BEGIN BULK” and “ENDDATA” are interpreted. (These words can also be lowercase.) In that case, all the lines before “BEGIN BULK” statement are ignored, and if no “BEGIN BULK” statement appears in the file, no line is interpreted.
If the “BulkOnly” Logical parameter is set to “true”, the lines in the file are assumed to correspond to lines if the Bulk Data Section of Nastran input. Then, lines “BEGIN BULK” and “ENDDATA” are ignored.
Generally, the “readBdf” method is called only once after the NastranDb object creation to initialize the finite element model. However, additional files might help to add FEM entities to the model. (For example, additional nodes used for the post-processing.)
When a FEM entity that is supposed to be defined only once in a model, is read several times, or already is defined in the DataBase before the call to “readBdf” method, only the last entity is kept.
One advises to limit the number of calls to the “readBdf” method because the method can be time consuming. Indeed, at the end of each call, FeResPost updates a large number of data structures in the “NastranDb” class, in this can take some time. (These data structures correspond, for example, to containers associating elements and properties, elements and materials, nodes and elements...) Therefore, a good way to work would be to read all the BDF files by a single call to “readBdf”, the file being read including different sub-files.
The method accepts the reading of cards in short format fields, large format fields, and free format fields. But for free format field, the separator must be a comma (“,”), and the card must be written on one single line.
Recognized Nastran cards are:
The “GRID”, “POINT”, “SPOINT” and “EPOINT” cards.
The following element cards: “CBAR”, “CBEAM”, “CBEND”, “CBUSH”, “CBUSH1D”, “CDAMP1”, “CDAMP2”, “CDAMP3”, “CDAMP4”, “CDAMP5”, “CELAS1”, “CELAS2”, “CELAS3”, “CELAS4”, “CFAST”, “CGAP”, “CHEXA”, “CMASS1”, “CMASS2”, “CMASS3”, “CMASS4”, “CONM2”, “CONROD”, “CPENTA”, “CPYRAM”, “CQUAD”, “CQUAD4”, “CQUAD8”, “CQUADR”, “CROD”, “CSHEAR”, “CTETRA”, “CTRIA3”, “CTRIA6”, “CTRIAR”, “CTUBE”, “CVISC” and “PLOTEL”.
The following rigid body elements: “RBE1”, “RBE2”, “RBE3”,“RROD” and “RBAR”.
The multipoint constraints cards: “MPC” and “MPCADD”.
The following coordinate system cards: “CORD1C”, “CORD1R”, “CORD1S”, “CORD2C”, “CORD2R”, “CORD2S” and “CORD3G”.
Note however that the support for “CORD3G” coordinate system is limited. In particular, Transformation from/to this type of coordinate system are not possible. Actually, the support is limited to the reading of the “CORD3G” card from Nastran BDF file (no reading from OP2), and the correct identification of the CS type in such a way that an exception can be thrown if unsupported CS transformation is attempt.
The following property cards: “PBAR”, “PBARL”, “PBEAM”, “PBEAML”, “PBUSH”, “PCOMP”, “PCOMPG”, “PDAMP”, “PDAMP5”, “PDAMPT”, “PELAS”, “PELAST”, “PFAST”, “PGAP”, “PMASS”, “PROD”, “PSHEAR”, “PSHELL”, “PSOLID”, “PTUBE” and “PVISC” are totally supported. The cards“PBEND”, “PBUSH1D”, “PBUSHT”, “PLPLANE” and “PLSOLID” are only partially supported1 .
Four material cards are totally supported: “MAT1”, “MAT2”, “MAT8” and “MAT9”. Some other material cards are only partially supported: “CREEP”, “MATS1”, “MATT1”, “MATT2”, “MATT8”, “MAT3”, “MATT3”, “MAT4”, “MAT5”, “MATT4”, “MATT5”, “MATT9”, “MAT10”, “MAT11” and “MATHP”.
The “include”, “rfinclude” or “rfalter” statement lines are taken into account, but with some limitations:
The include statements must obviously comply with Nastran “include” syntax. Note however that the rule that one first attempt an include of a file starting from the Nastran working directory is not implemented. (How could one determine in which directory the Nastran command has been run?) instead, the first include directory that is tested is the current working directory of FeResPost.
when strings are quoted, use single quotes, and not double ones.
When variations of base file names are tested, the “UNIX” rules are followed. (See MSC.Nastran manual.)
The logical symbols in path names are interpreted. However no extensive tests have been done to check that the programming is correct.
Comments in file names may lead to problems.
Quoted strings that span on several lines may lead to problems.
The blank character is not completely supported so that its use should be avoided in the definition of include file names.
Only ASCII characters should appear in the path specifying the BDF file. The “Verbosity” parameter of “readBdf” method can be used to make sure that the generated include paths comply with this rule. Again, this is more a recommendation that an imposition as special characters seem to be well supported on some platforms.
The examples given in “RUBY/EX01” directory should help the reader to identify the kinds of include statements that are accepted by FeResPost. (See section IV.2.2.1.)
In case of problems, we suggest:
To be “defensive” and “reasonable” when using “include” statements in its bulk Data Files.
To check that the “include” statements comply with Nastran rules and the recommendations given above.
To set the “verbosity” argument to true to debug FeResPost (or the Nastran model).
To report any problem with a small example, so that we can debug FeResPost if necessary.
At the end of reading, the method issues an information message with a list of cards that have been skipped.
The correct working of method “readBdf” has not been tested for many of the Nastran cards listed above. So, bugs are possible when testing FeResPost for new finite element models. In order to reduce the severity of such bugs, Four singleton methods defined in NastranDb class to disable or (re-)enable some of the Nastran cards. See section III.1.1.8 for the use of that method. Note that the disabling of Nastran cards also influences the “readOp2” method when model entities are read.
It is also possible to read a finite element model from an “op2” file with “readOp2” method. The model stored in the file is imported into the NastranDb if the second string argument of the method is “Model” or “Model/Results”. The first String argument is the name of the “op2” file.
The format of these files is described in [Rey04]. One describes in section III.1.1.2 the reading of finite element entities, and in section III.1.1.8 the reading of Results. The reading of 32bits as well as 64bits “op2” files is possible. However there is no advantage in reading 64bits version. Actually, these files are larger and may take a longer time to read.
Note that the reading of “op2” files also checks the endianness of the file and, if needed, does corrections to the binary data. For example, it can switch the reading from little endians to big endians or reversely. This allows “op2” files produced on a machine to be read on another machine with different “endianness” so that the portability of results is improved. Also, the 32/64 bits version is checked when the file is opened.
Finite element entities are read into the NastranDb with method “readOp2” if one specifies “Model” or “Model/Results” for the entities to read. The finite element entities recognized by the method corresponding to the Nastran cards supported by the “readBdf” method (see section III.1.1.1). The corresponding Data Blocks in the “op2” file are “GEOM1”, “GEOM2”, “GEOM3”, “GEOM4”, “EPT” and “MPT” (see [Rey04]).
Note that one generally prefers to read FE entities from a Bulk Data File than from an “op2” file because the data stored are sometimes ambiguous in the “op2” file (orientation of material properties on 2D elements,...). However, the reading of op2 files is faster than the reading of BDF files.
The correct working of method “readOp2” has not been tested for many of the Nastran cards listed above. So, bugs are likely to occur when testing FeResPost for new finite element models. In order to reduce the gravity of such bugs, The NastranDb class allows to disable or enable some of the Nastran cards. See section III.1.1.8 for the use of the corresponding singleton methods. Note that the disabling of Nastran cards also influences the “readBdf” method.
Since version 5.0.5 of FeResPost, Nastran superelements are partially supported. More precisely, PART and external superelements are supported. (See [Hex22] for a definition of the different types of superelements.) The support is limited to the reading of models containing superelements from BDF or op2 files, and to the reading of corresponding Results from op2, xdb or hdf5 files. The purpose of FeResPost is not to generate models, superelements, or manage the assembly of a model divided in several partitions.
The following Nastran BDF cards or instructions related to super elements are supported:
The “BEGIN SUPER ...” or “BEGIN BULK SUPER ...” statements that mark the limits between the different parts of the model.
The “SEBULK" cards that allow the replication of an existing superelement.
Other cards related to the management of superelements are unsupported: “SELABEL”, “SELOC”, “SECONCT”, “SEEXCLD”, “SEMPLN’, “SETREE”’...
A finite element model can also be read from a Nastran op2 file, even though this is not recommended. The reading of op2 file identifies the different partitions and builds the corresponding superelement databases.
When a model containing several partitions is read, the corresponding NastranDb object contains sub-databases corresponding to the different superelements. Each database is a distinct NastranDb object. The main database is the “master” database. The sub-databases correspond to the different partitions. Several methods allow to obtain a superelement database from the master database. Also, it is possible to retrieve the master database from a superelement NastranDb object. Each database, including the master database, is identified by a positive integer SEID. For master database SEID=0.
To ease the management of NastranDb objects, a reference counter is added to the C++ nastran::database class. It ensures that the master database and the superelement databases are destroyed at the same time when all references to any of the database for a given model have been freed.
The following methods of the NastranDb class are related to the management of superelements:
Integer attribute “SEID” returns the superelement integer ID of a given NastranDb object.
Integer attribute “RefCounter” returns the number of references to a NastranDb object. More precisely, it gives the number of references to the different NastranDb objects of a given model, as a single counter monitors the number of references to master database and associated superelement databases. Normally, this attribute is used for debugging purpose only.
Integer attribute “NbrSuperElements” returns the number of superelements stored in NastranDb. The master database is not considered as a superelement.
Method “getMaster” returns the master database of a given superelement NastranDb object. (The NastranDb object from which the method is called must correspond to a superelement.)
Method “getSuperElementIdFromPos” returns the superelement integer SEID at a give position in the list of superelements associated to the master database. The superelement databases are stored in order of increasing SEID in the list of superelements. if superelements are stored in the master database, the postion argument must be between 0 and .
Method “getSuperElementFromId” returns a NastranDb object corresponding to the superelement specified by its SEID. If no superelement with specified SEID is found in the master database, nil is returned.
Method “getSuperElementFromPos” returns a NastranDb object corresponding to the superelement specified by its position in the lsit of superelements. If no superelement with specified SEID is found in the master database, nil is returned.
Method “removeResultsAllSE” erases the Results stored in the master and superelement databases. Arguments of the method are the same as those of removeResults method in DataBase class. Method has two String arguments corresponding to the method of selection of Results and to an identifier respectively. The “Method” argument has three possible values: “CaseId”, “SubCaseId” or “ResId”. It specifies whether the Results to be deleted are identified by their load case name, their subcase name or their Result type name. The second String argument corresponds to the identifier of Results to be deleted.
Method “removeAllResultsAllSE” removes all the Results stored in master and superelement databases.
The behaviour of ther methods is affected by the presence of superelements:
“readBdf” identifies the partition of model and manages the master and superelement DataBases. The same is true for the “readOp2” method when it is used to read a model. (This is not a recommended practice, however.)
Methods that read results into the DataBase identify whether Results are related to the master DataBase (residual structure) or to one of the superelement DataBases. Results are then stored into the master DataBase and into the superelement DataBases. FeResPost manages the correspondence between Results and and the DataBases. Methods of the NastranDb class concerned by this behaviour are “readOp2”, “readOp2FilteredResults”, “readXdb” and “readHdf”. Methods “removeResultsAllSE” and “removeAllResultsAllSE” described above have been defined to ease the cleaning of Results from the different DataBases in one single operation.
The Result files attachement methods “attachXdb” and “attachHdf” are meant to be called from the master DataBase. They allow however to access Results related to the different superelements. (See below.) Similarly, the two methods “detachXdb” and “detachHdf” are called from the master DataBase.
The methods that read results to a Hash object return the results corresponding to the DataBase on which the method is called (master DataBase or one of the superelement DataBase). Methods concerned by this are:
“readXdb2H”, “getAttachmentResults”, “importAttachmentResults”,
“getAttachmentResultsCombili”, “getAttachmentElementExtId”, and
“getAttachmentNodeInfo” for the XDB files.
“readHdf2H”, “getHdfAttachmentResults” and “readHdfAttachmentResults” for the HDF files.
The other XDB or HDF attachment methods are not affected by the presence of superelements. Many of these methods can be called from the master DB or from one of the superelements. (For example: checkAttachmentExists, getAttachmentNames, getAttachmentWordsSize...)
Groups are managed per database. This means that one manages groups separately with master DB and each superelement database. For example, for the reading of Groups from Patran session files, readGroupsFromPatranSession must be called separately for each database and with distinct session files.
Examples discussed in section IV.2.11 should clarify the management of models and Results with superelements, and the information provided here.
Method “writeBdfLines” is used to output the model or part of the model into a text file with a format compatible with Nastran BDF cards. The method has 5 or 6 arguments :
A string containing the name of the file to which the Nastran cards are printed.
A string corresponding to the opening mode for the file. Valid values are “w” and “w+” (for append mode).
A first format String argument specifying whether the fields in the cards output are left or right aligned. This argument may have three values: “left”, “right” or a void String. If the String is void, the format defaults to “left”.
A second format String argument specifying whether the fields in the cards output are narrow or wide. This argument may have three values: “short”, “wide” or a void String. If the String is void, the format defaults to “short”.
A third String argument corresponding to the type of entities that must be printed. The method scans the String argument and searches sub-strings that specify whether an entity type is to be printed or not. The sub-strings that are searched are “All”, “CoordSys”, “Nodes”, “Elements”, “RBEs”, “MPCs”, “Properties”, “Materials”.
The last argument is optional and corresponds to the Group for which cards are to be printed. It can be a String or a Group argument. If its type is String, then the corresponding Group defined in the DataBase is considered. Note that “Properties” and “Materials” are not printed if the Group argument is provided.
The “writeBdfLines” method must be used for debugging purposes only. The user must keep in mind that some entities are not totally supported and their output may be problematic.
One first singleton method may be used to output formatted Nastran cards. This method can be used, for example, to produce Nastran cards for inclusion in a Bulk Data File. The method name is “writeNastranCard” and has five or six arguments (the “output card name” argument is optional):
A String containing the name of the file to which the Nastran card is printed.
A String corresponding to the opening mode for the output file. Valid values are “w” and “w+” (for append mode).
A first format String argument specifying whether the fields in the card output are left or right aligned. This argument may have three values: “left”, “right” or a void String. If the String is void, the format defaults to “left”.
A second format String argument specifying whether the fields in the card output are narrow or wide. This argument may have three values: “short”, “wide” or a void String. If the String is void, the format defaults to “short”.
A String corresponding to the name of the output card. This name cannot have more than 8 characters and should correspond to a valid Nastran BDF card name. THIS ARGUMENT IS OPTIONAL.
An Array containing the fields to be printed. Possible types for the elements of this Array are Real, Integer and String:
If the previous “output card name” argument is omitted (5 arguments), then the first element of the Array must be a String corresponding to the output card name (Nastran card field 1).
if the previous “output card name” argument is given (method is called with 6 arguments), then the Array values start with Nastran card field 2 content.
Examples of calls to the method follow:
NastranDb.writeNastranCard("output.bdf","w+","right","short",card)
NastranDb.writeNastranCard("output.bdf","w+","right","short","RBE2",card)
Another singleton method called “writeNastranCards” allows to output several Nastran cards. This method has the same arguments as “writeNastranCard” except that the last argument is an Array of Arrays, each element of the “big” Array corresponding to one Nastran card. The other arguments are the same, which means:
If the number of arguments of the method is 5, the first element of each “card” Array must be a String corresponding to the Nastran card name.
If the number of arguments is 6, then the output card name argument is given and common to all the Nastran output cards. Then, the card name must not be included as first element of the different Nastran card Arrays.
Remark that when “writeNastranCards” is called with 5 arguments, it is possible, with a single call, to output different types of Nastran cards (“FORCE”, “MOMENT”,...). This is not possible when the method is called with 6 arguments. Examples of calls to the method follow:
NastranDb.writeNastranCards("output.bdf","w+","right","short",cards)
NastranDb.writeNastranCards("output.bdf","w+","right","short","RBE2",cards)
The use of “writeNastranCard” and “writeNastranCards” methods is clarified in section IV.2.5.1.
Method “writeNastranCardToVectStr” is similar to “writeNastranCard”. It produces a formatted BDF output but returns it in an Array of Strings, each String corresponding to one line in the output. The three or four arguments of the method are as follows:
A first format String argument specifying whether the fields in the card output are left or right aligned. This argument may have three values: “left”, “right” or a void String. If the String is void, the format defaults to “left”.
A second format String argument specifying whether the fields in the card output are narrow or wide. This argument may have three values: “short”, “wide” or a void String. If the String is void, the format defaults to “short”.
A String corresponding to the name of the output card. This name cannot have more than 8 characters and should correspond to a valid Nastran BDF card name. HERE AGAIN, THE ARGUMENT IS OPTIONAL.
An Array containing the fields to be printed. Possible types for the elements of this Array are Real, Integer and String:
If the previous “output card name” argument is omitted (3 arguments), then the first element of the Array must be a String corresponding to the output card name (Nastran card field 1).
if the previous “output card name” argument is given (method is called with 4 arguments), then the Array values start with Nastran card field 2 content.
Examples of calls to these two methods follow:
lines=[]
lines+=NastranDb.writeNastranCardToVectStr("right","short",card)
lines+=NastranDb.writeNastranCardToVectStr("right","short","RBE2",card)
lines+=NastranDb.writeNastranCardsToVectStr("right","short",cards)
lines+=NastranDb.writeNastranCardsToVectStr("right","short","RBE2",cards)
puts lines
As has been done for the “writeNastranCard” method, a “writeNastranCardsToVectStr” singleton method is defined in the “NastranDb” class. A single call to the method allows the output of several Nastran cards in an Array of Strings. The last argument of the method is an Array or Arrays.
The “fillCard” method allows to retrieve an Array corresponding to the a Nastran BDF card. The method has two arguments:
A String corresponding to the type of entity of which one requires the definition. Possible values of the argument are “CoordSys”, “Element”, “Node”, “RBE”, “MPC”, “Property” and “Material”.
An integer corresponding to the ID of the FEM item of which one searches the definition.
The method returns the definition in an Array:
The first element of the Array (corresponding to index 0), is a String containing the name of the Nastran card.
Elements 1 to 8 correspond to the first line in the card definition (small field format).
Elements 9 to 16 correspond to the second line in card definition (small field format).
For each line, the fields 1 and 10 are neglected, except for the first line in which field 1 contains the name of the Nastran card.
Note that Nastran model may contain several material cards sharing a common ID, or several MPC cards with the same ID. When this case occurs, an exception is thrown. Therefore, for MPC or material cards, it is advised to use “fillCards” method instead of “fillCard”. An exception is also thown when no FEM item matching specified ID is found.
The “fillCards” method allows to retrieve an Array containing BDF cards as those returned by “fillCard” method. (This means that “fillCards” method returns an Array of Arrays.) The method has two or three arguments:
A String corresponding to the type of entity of which one requires the definition. Possible values of the argument are “CoordSys”, “Element”, “Node”, “RBE”, “MPC”, “Property” and “Material”.
An integer corresponding to the minimum ID of the FEM items of which one searches the definitions.
An integer corresponding to the maximum ID of the FEM items of which one searches the definitions.
Third argument is optional. When omitted, one considers that maximum ID = minimum ID. In such cases, the method generally returns maximum one BDF card. However, for materials and MPCs, a single ID may correspond to several items. The method returns the definition in an Array of Arrays. Each element of the main Array is a Nastran BDF card as those returned by “fillCard” method.
Method “insertCard” performs the reverse operation: it allows to update the “NastranDb” database by insertion of FEM entity (coordinate system, node, element, RBE, material...). The method “insertCard” has one argument: an Array containing the different fields of the card. The conventions for the components of the Array are exactly the same as for the Array returned by method “fillCard” discussed above. (This means that first element of the Array, of index 0, is a String corresponding to the name of the Nastran card.)
Method “insertCards” corresponds to “insertCard” but allows to insert several cards with a single call to the method. The argument of the method is then an Array of Arrays.
Remarks about the insertion methods:
We strongly advise to use “insertCards” method instead of “insertCard” to limit the number of calls to the method. Indeed, at the end of each insertion, FeResPost updates a large number of data structures in the “NastranDb” class, in this can take some time. (These data structures correspond, for example, to containers associating elements and properties, elements and materials, nodes and elements...) Therefore, a good way to work would be to collect all the cards to be inserted in the model in a big Array, and perform the insertion operation only once.
If one inserts a FEM entity that already exists in the database, the pre-existing entity is replaced by the new one. If an entity is defined twice in the argument cards, only the last card will remain inserted in the database at the end.
The “CoordSys” class allows the manipulation of coordinate systems for post-processing purpose. This class is presented in Chapter I.2. One presents below the methods of NastranDb class devoted to the manipulation of coordinate systems.
The “getCoordSysCopy” method returns a CoordSys object which is a copy of a coordinate system stored in the DataBase. The method has one integer argument which is the index of the coordinate system.
Note that the CoordSys returned by the method may be a “generic” CoordSys as presented in Chapter I.2, or a Nastran coordinate system.
The “addCoordSys” method is used to add a coordinate system to the DataBase. The argument of the method is the CoordSys object. In the DataBase, the object is referenced by its index.
If a coordinate system with the same index already exists in the NastranDb, it is replaced by the new coordinate system. In that case, the user is responsible for all the modifications involved in the finite element model by the possible modification of the NastranDB coordinate system. Therefore, it is considered as a good practice not to modify a coordinate involved in the finite element model definition.
Note that the coordinate system index must be a strictly positive integer. Also, the CoordSys inserted by the method may be a “generic” CoordSys as presented in Chapter I.2, or a Nastran coordinate system.
This method updates the definition wrt 0 (most basic coordinate system) of all the coordinate systems stored in a NastranDB. This operation is necessary when a coordinate system of the NastranDB has been modified, because the definitions of other coordinate systems wrt 0 may be affected.
The list of “NastranDb” methods returning Groups defined by association follows:
“getElementsAssociatedToNodes” returns a Group containing the list of elements associated to the nodes of the Group argument.
“getElementsAssociatedToMaterials” returns a Group containing the list of elements associated to the material(s) given as argument(s). The argument is an integer or an Array of integers corresponding to the material IDs of the elements inserted in the list.
“getElementsAssociatedToProperties” returns a Group containing the list of elements associated to the property (properties) given as argument(s). The argument is an integer or an Array of integers corresponding to the property IDs of the elements inserted in the list.
“getElementsAssociatedToPlies” returns a Group containing the list of elements associated to the ply (plies) given as argument(s). The argument is an integer or an Array of integers corresponding to the ply IDs of the elements inserted in the list. The ply Ids are the global ply identifiers referenced by PCOMPG Nastran data cards (Nastran model).
“getNodesAssociatedToElements” returns a Group containing the list of nodes associated to the elements of the Group argument.
“getNodesAssociatedToRbes” returns a Group containing the list of nodes associated to the rigid body elements of the Group argument.
“getRbesAssociatedToNodes” returns a Group containing the list of rigid body elements associated to the nodes of the Group argument.
Several methods allow the reading of results from an “op2” file or to tune the behavior of reading this file. These methods are described below. The reading of 32bits as well as 64bits “op2” files is possible. However there is no advantage in reading 64bits version. Actually, these files are larger and may take a longer time to read.
Note that one strongly advises to attribute an integer ID, and a name to each sub-case defined in Nastran BDF file. For example, in the following example, the sub-case integer ID is 201, and its name is “ORBIT_ONE_MS2_X”:
SUBCASE 201 SUBTITLE=ORBIT_ONE_MS2_X SPC=702001 LOAD=601001
“readOp2” method is used to read FEM entities or Results into the DataBase from an “op2” file generated by Nastran. This method is also discussed in section III.1.1.2 for the reading of finite element model. Here, one discusses more precisely the reading of Results.
The method has up to 7 arguments:
A String that corresponds to the path to file from which model or Results are read.
A String that corresponds to the entities that are being read. Possible values of the second argument are “Model/Results”, “Model” and "Results". Generally, only the third possible argument is used.
A “LcNames” argument that corresponds to the list of load cases for which the Results are read. The argument may be:
A Single String corresponding to the name of one load case.
An Array of Strings corresponding to the list of load cases for which Results are read.
If this argument is omitted, or nil, or if the Array argument contains no elements, the Results of ALL load cases are read.
A “ScNames” argument that corresponds to the list of subcases for which the Results are read. The argument may be:
A Single String corresponding to the name of one subcase.
An Array of Strings corresponding to the list of subcases for which Results are read.
If this argument is omitted, or nil, or if the Array argument contains no elements, the Results of ALL subcases are read.
A “ResNames” argument that corresponds to the list of Results identifiers for which the Results are read. The argument may be:
A Single String corresponding to the Result ID.
An Array of Strings corresponding to the list of Result IDs for which Results are read.
If this argument is omitted, or nil, or if the Array argument contains no elements, ALL Results are read.
A “PostParam” integer argument corresponding to the parameter “POST” in Nastran Bulk Data File. Possible values of the parameter:
“-1” (for Patran output).
“-2” (for EDS I-DEAS output). It seems to correspond also to the output produced by Autodesk’s Inventor Nastran with “PARAM POST -1”.
The default value of this argument is “-1” (op2 created for Patran). Note that readOp2 will not work with the values “-4’ and “-5” which are valid POST parameters for Nastran.
An optional“NasVersion” real argument corresponding to an MSC version. For example 2021.2 can be used for MSC version 2021.2. This parameter influences the reading of some IFP tables whose format have changed. Default value is 2019.99.
The third, fourth, fifth and sixth arguments can be omitted. Note that Ruby identifies the type of arguments by their order of appearance in the list. So, if “LcNames” argument is omitted, but “ScNames” or “ResNames” argument is used, the “LcNames” must be a void Array (“[]”) or “nil”. Examples of possible calls to “readOp2” method follow:
...
db.readOp2("../../EXEC/orbit_unit_xyz.op2","Results")
...
db.readOp2("../../EXEC/orbit_unit_xyz.op2","Results",\
"GRAV_X")
...
db.readOp2("../../EXEC/orbit_unit_xyz.op2","Results",\
["GRAV_X"])
...
db.readOp2("../../EXEC/orbit_unit_xyz.op2","Results",\
["GRAV_X", "GRAV_Y"])
...
db.readOp2("../../EXEC/orbit_unit_xyz.op2","Results",\
[],[],"Stress Tensor")
...
db.readOp2("../../EXEC/orbit_unit_xyz.op2","Results",\
[],[],["Stress Tensor", "Shell Forces", Shell Moments"])
...
db.readOp2("../../EXEC/orbit_unit_xyz.op2","Results",\
["GRAV_X", "GRAV_Y"],"Statics",\
["Stress Tensor", "Shell Forces", Shell Moments"])
...
db.readOp2("../../EXEC/orbit_unit_xyz.op2","Results",\
[],[],[],-2,2021.2)
...
“readOp22H” method is used to read Results from an “op2” file generated by Nastran. The Results are returned into an Hash object. The method has nearly the same arguments as “readOp2”, but the “what” argument is missing:
“Path” argument,
“LcNames” argument,
“ScNames” argument,
“ResNames” argument,
“PostParam” integer argument,
“NasVersion” real argument.
(See the description of “readOp2” method for more information.) Example of use:
...
h=db.readOp22H("../../EXEC/orbit_unit_xyz.op2",[],[],[],-2)
...
“readOp2FilteredResults” method is used to read Results into the DataBase from an “op2” file generated by Nastran. This method does not allow the reading of finite element model. It differs from “readOp2” method by the fact that its parameters allow a filtering of the Results that are read into the database. This filtering may be mandatory when an op2 is very large and a finer selection of the results is needed. For example:
Select only some Result types, like stresses, or forces, or accelerations.
Select only some frequency outputs, or eigen modes, or time steps.
Read the random RMS results but not the associated complex results,
...
The method has from 1 to 10 arguments:
A String that corresponds to the path to file from which Results are read.
An “LcFilters” String argument that corresponds to the load cases for which the Results are read. The argument may be:
A Single String corresponding to a regular expression for load cases selection.
An Array of Strings defining several regular expressions for the selection of load cases to be read.
If this argument is omitted, or nil, or if the Array argument contains no elements, the Results of ALL load cases are read.
An “ScFilters” String argument that corresponds to the sub-cases for which the Results are read. The argument may be:
A Single String corresponding to a regular expression for sub-cases selection.
An Array of Strings defining several regular expressions for the selection of sub-cases to be read.
If this argument is omitted, or nil, or if the Array argument contains no elements, the Results of ALL sub-cases are read.
A “ResFilters” String argument that corresponds to the types of Results that are read. The argument may be:
A Single String corresponding to a regular expression for Results selection.
An Array of Strings defining several regular expressions for the selection of Results.
If this argument is omitted, or nil, or if the Array argument contains no elements, the Results of ALL types of Results are read.
A “PostParam” integer argument corresponding to the parameter “POST” in Nastran Bulk Data File. Possible values of the parameter:
The default value of this argument is “-1” (op2 created for Patran). Note that readOp2 will not work with the values “-4’ and “-5” which are valid POST parameters for Nastran.
An “IMin” integer argument. (See below.)
An “IMax” integer argument. The ‘IMin” and “IMax” arguments allow to filter results on integer parameter associated to the output (mode integer ID, Step output...).
An “RMin” real argument. (See below.)
An “RMax” real argument. The ‘RMin” and “RMax” arguments allow to filter results on real parameter associated to the output (frequency for modal analysis, time step for non-linear or transient analysis, Frequency output for dynamic vibration or random analysis...).
An optional“NasVersion” real argument corresponding to an MSC version. For example 2021.2 can be used for MSC version 2021.2. This parameter influences the reading of some IFP tables whose format have changed. Default value is 2019.99.
Ruby identifies the type of arguments by their order of appearance in the list. So, if “LcFilters” argument is omitted, but “ScFilters” or “ResFilters” argument is used, the “LcFilters” must be a void Array (“[]”) or “nil”.
The regular expressions used for arguments 2, 3 and 4 follow the ECMAScript syntax. Examples of valid calls to “readOp2FilteredResults” follow:
...
db.readOp2FilteredResults(op2Name,nil,"Out(.*)",".*\\(MP\\).*",
nil,3,7)
...
db.readOp2FilteredResults(op2Name,nil,"Out(.*)",".*\\(MP\\).*",
nil,nil,nil,102.5,108.5)
...
db.readOp2FilteredResults(op2Name,nil,".*Out.*",nil,
nil,nil,nil,102.5,108.5)
...
db.readOp2FilteredResults(op2Name,nil,".*CRMS.*",nil,
nil,nil,nil,102.5,108.5)
...
db.readOp2FilteredResults(op2Name,nil,".* RMS .*")
...
db.readOp2FilteredResults(op2Name,nil,".* RMS.*")
...
Note that regular expressions can be replaced by a simple name except that “special characters” must be escaped (for example “\\(” or “\\)”).
“readOp2FilteredResults2H” method is used to read Results from an “op2” file generated by Nastran. Results are returned in a Hash object. The method has the same arguments as “readOp2FilteredResults”. Examples of use:
...
h=db.readOp2FilteredResults2H(op2Name,nil,"Out(.*)",".*\\(MP\\).*",
nil,3,7)
...
h=db.readOp2FilteredResults2H(op2Name,nil,".* RMS.*")
...
Note that “readOp2FilteredResults” method providing regular expressions is provided for the importation of Results from OP2 files, but not from XDB or HDF files. This has been done because the reading of OP2 file is done sequentially. This means that the entire file is read each time is accessed via “readOp2” or “readOp2FilteredResults” methods. For the reading of XDB or HDF content, random access is possible and the use of attachment is recommended for large files. Also, it is possible to obtain the lists of load cases, sub-cases and Results present in XDB and HDF files, so that filtered reading from these files remains possible by specifying lists of load cases, sub-cases or Results obtained by calling “getXdbLcInfos”, “getAttachmentLcInfos” or “getHdfAttachmentLcInfos” methods.
Six singleton methods allow to disable or (re-)enable some entities when importing model or result entities from Nastran op2 or bdf files, or to check the status of the bdf cards or Results:
“enableBulkCards” is used to re-enable some Nastran card when reading model entities from a Nastran bdf or op2 file.
“disableBulkCards” is used to disable some Nastran card when reading model entities from a Nastran bdf or op2 file.
“getBulkCardsEnableInfos” returns a Hash with String keys and Boolean values that associates the enabled/disabled status to the different BDF card names.
“enableOp2ResElems” is used to re-enable “result element types” when reading Results from an op2 file.
“disableOp2ResElems” is used to disable “result element types” when reading Results from an op2 file.
“getOp2ResElemsEnableInfos” returns a Hash with String keys and Boolean values that associates the enabled/disabled status to the different BDF card names for results reading from op2 files.
The four enable/disable methods take one String, or an Array of Strings argument. The Strings correspond to the names of the entities that must be disabled or enabled. The “enable info” methods have no argument.
Other methods devoted to enable or disable composite layered Results are defined in the generic “DataBase” class. These methods are presented in section I.1.3.2.
These enable/disable methods can be set to filter the results importation in order to reduce the computation time, or the memory usage. The methods can also be used to prevent FeResPost in the hopefully rare case when a bug occurs in the program for the reading of a particular element, or the reading of the corresponding Results from an op2 file.
Presently, only some of the result data blocks of the file can be read:
The “OUG” block corresponds to displacements, velocities, accelerations, temperatures...
The “OGPFB1” block corresponds to Grid Point Forces.
The “OES” blocks correspond to strains or stresses. The names of blocks that can be read are: “OSTR1”, “OSTR1C”, “OES1C” and “OES1X”.
The “OPG1” block corresponds to applied loads at nodes.
The “OEF” blocks correspond to results in composite parts of the structure, or to forces in surfacic or 1D elements. The names of blocks that can be read are: “OEFIT” and “OEF1C”.
The “OQG” blocks correspond to MPC or SPC forces.
The correspondence between the Nastran output requests and the DMAP data blocks written in the “op2” file is given in Tables III.1.7 to III.1.14. Also one gives in the Tables the type names of Results generated in the NastranDb by “readOp2” method. The solution sequences for which Results can be read from an “op2” are:
SOL 101: linear static or thermal analysis,
SOL 103: linear eigen-values analysis,
SOL 105: buckling analysis,
SOL 106: non-linear static analysis,
SOL 108 and 111 : frequency response analysis + associated random analysis results.
SOL 129: non-linear transient analysis,
SOL 159: transient thermal analysis,
SOL 400: non-linear static or transient analysis (corresponds to the SOL106 and SOL129 analyses).
Several methods allow the reading of Result entities or characteristics stored in an xdb file. Real Results as well as Complex ones can be read from xdb files. This last format of Results can for example be read from a Nastran “xdb” result file corresponding to a SOL107, SOL108 or SOL111.
The reading of 64bits XDB files, as well as 32bits XDB files is possible. Note however that the results that are read are stored in 32bits integer/real values so that there is no advantage in using 64bits XDB files with FeResPost. (It probably slows down the XDB access.)
The use of Nastran "DBCFACT=4" parameter is supported. This parameter generates XDB files with BBBT index (Binary Blocked Balanced Tree Method of entry key storage), instead of Hash storage. The default Nastran seems to be "DBCFACT=0" and corresponds to an Hash Key (HK) of key storage.
Remark: one strongly advises to attribute an integer ID, and a name to each sub-case defined in Nastran BDF file. For example, in the following example, the sub-case integer ID is 201, and its name is “ORBIT_ONE_MS2_X”:
SUBCASE 201 SUBTITLE=ORBIT_ONE_MS2_X SPC=702001 LOAD=601001
For all the methods listed in this section, the first argument is a String containing the path to the XDB file. The methods do not require the XDB file to be attached to the Nastran database. However the corresponding methods exist for XDB result files that have been attached to a database. (The corresponding methods with XDB attachments are described in section III.1.1.10.)
The supported elements for extraction of Results is summarized in Table III.1.2. Note that the CPYRAM element does not appear in Table III.1.2. It seems that MSC Nastran outputs no stress/strain results in XDB file, despite the fact that results are saved in OP2 and HDF files.
| Element | Nastran | MSC. Access | FeResPost |
| Name | Element ID | Element ID | Element Id |
| CBAR | 12 | 34 | 1 |
| CQUAD4 | 1 | 33 | 2 |
| CTRIA3 | 4 | 74 | 3 |
| CHEXA | 2 | 67 | 4 |
| CROD | 9 | 1 | 5 |
| CBEAM | 10 | 2 | 6 |
| CPENTA | 6 | 68 | 7 |
| CBUSH | 47 | 102 | 8 |
| CTETRA | 14 | 39 | 9 |
| CTRIA6 | 7 | 75 | 10 |
| CQUAD8 | 3 | 64 | 11 |
| CQUAD4(X) | 95 | 171 | 12 |
| CELASi | 16...19 | 11...14 | 13 |
| CONM1 | 30 | 29 | 14 |
| CONM2 | 31 | 30 | 15 |
| CFAST | ??? | ??? | 16 |
| CONROD | 8 | 10 | 17 |
| CSHEAR | 11 | 4 | 18 |
| CGAP | 15 | 38 | 19 |
| CQUADR | 29 | 82 | 20 |
| CTRIAR | 34 | 70 | 21 |
| CWELD | 53 | 200 | 22 |
| CBAR(X) | 13 | 100 | 23 |
“getXdbLcNames” singleton method returns an Array of String containing the list of load cases to which Results found in an xdb file correspond. The arguments are:
A String specifying the access path to the xdb file.
A Boolean value specifying whether one forces the swap of endianness when reading the XDB file.
The second argument is optional.
“getXdbScNames” singleton method returns an Array of String containing the list of sub-cases to which Results found in an xdb file correspond. The arguments are:
A String specifying the access path to the xdb file.
A Boolean value specifying whether one forces the swap of endianness when reading the XDB file.
The second argument is optional.
“getXdbResNames” singleton method returns an Array of String containing the Result type names to which Results found in an xdb file correspond. The arguments are:
A String specifying the access path to the xdb file.
A Boolean value specifying whether one forces the swap of endianness when reading the XDB file.
The second argument is optional.
“getXdbLcScNames” singleton method returns an Array of two elements containing:
An Array of Strings containing the list of load cases to which Results found in the xdb file correspond.
An Array of Strings containing the list of sub-cases to which Results found in the xdb file correspond.
The arguments are:
A String specifying the access path to the xdb file.
A Boolean value specifying whether one forces the swap of endianness when reading the XDB file.
The second argument is optional.
“getXdbLcScResNames” singleton method returns an Array of three elements containing:
An Array of Strings containing the list of load cases to which Results found in the xdb file correspond.
An Array of Strings containing the list of sub-cases to which Results found in the xdb file correspond.
An Array of Strings containing the list of Result types to which Results found in the xdb file correspond.
The arguments are:
A String specifying the access path to the xdb file.
A Boolean value specifying whether one forces the swap of endianness when reading the XDB file.
The second argument is optional.
“getXdbLcInfos” singleton method returns information about the load cases and sub-cases for which Results are stored in a xdb file. The arguments are:
A String specifying the access path to the xdb file.
A Boolean value specifying whether one forces the swap of endianness when reading the XDB file.
The second argument is optional.
The method returns an Array of Arrays. Each element of the Array contains the information for one load case and sub-case identification:
A String corresponding to the name of the load case.
A String corresponding to the name of the sub-case. (As defined for modal analyses, non-linear analyses...).
A third String argument (unused so far).
The first integer ID of the corresponding Results (usually, the load case ID).
The second integer ID of the corresponding Results (usually, a mode ID, or a step ID...).
The first real associated value (frequency, real eigen-value, real part of a complex eigen value or continuation parameter...).
The second real associated value (imaginary part of a complex eigen-value).
“printXdbDictionnary” singleton method prints the dictionnary of an XDB file. The arguments are:
A String specifying the access path to the XDB file.
A String specifying the access path to an output file.
A Boolean value specifying whether one forces the swap of endianness when reading the XDB file.
The second and third arguments are optional. If the second argument is omitted or a void String, the dictionnary is printed on standard output.
This method has been added for debugging purpose: it helps to identify the XDB tables that are read, and those which are not.
The “readXdb” method is used to read Results into the DataBase from an “xdb” file generated by Nastran. (Only Results can be read from a Nastran “xdb” file.) The method has up to five arguments:
A String argument that corresponds to the name of the file from which Results are read.
A String or an Array of Strings corresponding to the names of load cases for which Results are imported into the DataBase. If the Array is void or the parameter is omitted, all load cases in xdb result files are considered when results are read.
A String or an Array of Strings corresponding to the names of subcases for which Results are imported into the DataBase. If the Array is void or the parameter is omitted, all sub-cases in xdb result files are considered when results are read.
A String or an Array of Strings corresponding to the identifiers of Results for which Results are imported into the DataBase. If the Array is void or the parameter is omitted, all Results of xdb result files are considered when results are read.
A Boolean value specifying whether one forces the swap of endianness when reading the XDB file.
All parameters, except the first one, can be omitted. Then the method assumes that a void Array has been passed as argument.
Results that can be read are listed below:
Nodal displacements (translations and rotations),
Nodal temperatures,
SPC forces and moments,
MPC forces and moments,
Grid Point Forces,
Element forces and moments,
Element stresses,
Element strains,
Element Strain and kinetic energies, and energy loss.
Composite ply stresses and strains.
Composite failure indices do not seem to be output in the xdb file. Only a few elements are supported. However, the most important ones are read:
0D elements: CONM1 and CONM2 (for kinetic energy),
1D elements: CBAR, CBEAM, CGAP, CELAS1, CELAS2, CELAS3, CELAS4, CROD, CBUSH and CFAST.
2D elements: CTRIA3, CQUAD4, CTRIA6, CQUAD8, CQUADR and CTRIAR.
3D elements: CHEXA, CPENTA and CTETRA (but not CPYRAM).
The different characteristics of imported Results correspond to the characteristics of corresponding Results read from “op2” files.
Note however, that Complex Results can also be read from xdb files. Generally, the complex Results are the same as the real Results. More information can be found in section X.C.2.
Four methods devoted to the enabling or disabling composite layered Results are defined in the generic “DataBase” class. These methods are presented in section I.1.3.2.
The “readXdb2H” method is used to read Results from an “xdb” file generated by Nastran and returns the Results in a Hash object. Arguments are the same as those of “readXdb” method.
MSC.Nastran is distributed with “TRANS” and “RECEIVE” tools that allow to exchange XDB files on machines with different ENDIAN conventions. This is sometimes necessary, for example, when Patran and Nastran are run on different machines. On the other hand, FeResPost allows the identification of endianness in XDB files (in most cases). In some cases, the user must “force” the choice.
The different methods devoted to XDB files access allow to specify a force on swap endianness. When the corresponding parameter is set to “TRUE”, FeResPost considers that the endianness of binary XDB file does not correspond to the endianness of the machine on which FeResPost executes. Then, a swap of endianness is performed when the binary file is read.
If the “SwapEndianness” parameter is set to false, no modification of endianness is done when the file is read.
If the “SwapEndianness” parameter is not given, FeResPost checks the endiannes of the file and, if needed, does corrections to the binary data that are read. The test is done as follows:
FeResPost reads five of the first words in the XDB file. (Words 5, 8, 11, 12 and 15, index 0 corresponding to the first word at beginning in the file.)
Each of these words is supposed to correspond to a positive integer value smaller than 65536. Hence, only the two less significant bytes of the words should be different than zero.
The test is done on the five integers and for each one, one attempts to guess if the endianness is “big” or “little”. The result for word 15 determines which kind of endianness is adopted. This word seems to correspond to “DATA BASE OPEN MODE FLAG” and has been selected because one assumes that it always has a very small value.
if the five words do not lead to the same conclusion, a warning message is issued. (This might help the user to identify the source of the problem.)
Three singleton methods allow to activate or deactivate the reading of Results from XDB files. More precisely, the XDB results are presented in different tables that correspond to:
The type of Result (stresses, forces, displacements,...),
The type of element (CBAR, CQUAD4...),
The format (real, complex,...).
Each type of Table can be enabled or disabled separately. This can be useful to filter the importation of Results. Also, if there is a FeResPost bug in the reading of a given Result table, the disabling of this table allows to continue to work with the other results while the development team works to fix the problem.
The three singleton methods devoted to XDB table activation are:
“enableXdbTables” is used to re-enable an XDB Result table for XDB Result reading.
“disableXdbTables” is used to disable an XDB Result table for XDB Result reading.
“getXdbTablesEnableInfos” returns a Hash with String keys and Boolean values that associates the enabled/disabled status of the different XDB tables. (This method also gives you the names of the different XDB tables that can be read from XDB files.)
The two enable/disable methods take one String, or an Array of Strings argument. The Strings correspond to the names of the entities that must be disabled or enabled. The “enable info” method has no argument.
Since version 3.4.0, FeResPost allows a random access to XDB result files. This method is more efficient than the methods that import XDB Results into the DataBase, and extracting copies of these Results. A peculiar case in which the random access methods will be more efficient is when only some small parts of the XDB file are of interest to the programmer.
The principle of random access is the same as the attachment of XDB files to a Patran DataBase:
The XDB file is attached to the DataBase.
Its content (lists of load cases, sub-cases and Results) is identified.
The Results that are needed are then read from the file.
The different methods called to perform these operations are described in the following sub-sections. These methods correspond more or less to the methods described in section III.1.1.9.
The method “attachXdb” is used to attach an XDB file to the Nastran DataBase. This method has up to two arguments:
The first argument is a String containing the name of the XDB file. (Full path name must be provided.)
The second argument is an optional Boolean parameter specifying whether the endianness must be swapped when XDB file content is read. If the parameter is not given, the endianness of the file is automatically detected. Note however that this check might fail. (See also page 578 for more information.)
Several other methods are used to manage the Xdb attachments to a DataBase:
“detachXdb” is used to delete an XDB attachment. The method has one String argument corresponding to the name of the XDB file.
“removeAllAttachments” removes all the XDB file attachments to a DataBase. This method has no argument.
“getNbrAttachments” has no argument and returns the number of XDB files attached to the DataBase.
“getAttachmentNames” has no argument and returns an Array of Strings containing the list of XDB files attached to the DataBase.
“checkAttachmentExists” has one String argument containing the XDB file name, and returns “True” if the XDB file is Attached to the DataBase, and “False” otherwise.
The following methods extract information related to the Results stored in an XDB file attached to the DataBase:
“getAttachmentWordsSize” returns the size of words in a specified XDB attachment. The size is given in bytes (4 or 8 bytes).
“getAttachmentSwapEndianness” returns true if the reading of XDB binary data involves a swap of words endianness, and false otherwise. (A swap of endianness is required when the endian convention of the machine on which Nastran solver has been run differs from the endianness of the machine on which XDB file is read.)
“getAttachmentLcInfos” returns information on load cases and sub-cases of Results found in the attached XDB file. The information is returned in an Array. (More information about the content of this Array is given in the description of method “getXdbLcInfos”. page 574.)
“getAttachmentNbrLoadCases” returns the number of load cases found in an XDB file.
“getAttachmentLcNames” returns an Array of Strings corresponding to the load case names found in the XDB file.
“getAttachmentLcScNames” returns an Array containing two elements. The first element is an Array of String containing the load case names found in the XDB file. The second element is an Array of String containing the sub-case names found in the XDB file.
“getAttachmentLcScResNames” returns an Array of three elements. Each element is an Array of Strings. The first element is the list of load case names. The second element is the list of sub-case names. The last element is the list of Result names.
All these methods have a single String argument containing the name of the XDB file that must have been previously attached to the DataBase. On the other hand, the following methods have one or two arguments:
“getAttachmentNbrSubCases” returns the number of sub-cases found in an XDB file.
“getAttachmentScNames” returns an Array of Strings corresponding to the sub-case names found in the XDB file.
“getAttachmentNbrResults” returns the number of Result names identified in the XDB attached file.
“getAttachmentResIds” returns an Array of Integers corresponding to the identifiers of the Results found in the XDB file.
“getAttachmentResNames” returns an Array of Strings corresponding to the names of the Results found in the XDB file.
The first argument is the name of the XDB file that must have been previously attached to the DataBase. The second argument is optional and corresponds to the name of a load case found in the attached XDB file. If the argument is not provided, all the load cases are investigated to build the list of sub-cases or Result names or IDs. If the argument is provided, only the sub-cases or Results of the corresponding load case are considered. If the provided load case does not exist in XDB attachment an error message is issued.
The method “getAttachmentResults” is used to read Results from the XDB file. The Results are directly returned by the method to the caller in a Hash object. They are not inserted in the DataBase from which the method is called.
The method has minimum four arguments:
A String corresponding to the name of XDB file attachment from which Results are read. (This file must have been previously attached to the DataBase.)
A String corresponding to the name of the load case for which Results are read.
A String or an Array of Strings corresponding to the names of sub-cases for which Results are read.
A String or an Array of Strings corresponding to the names of Results for which Results are read. The Result name provided as arguments must be considered as “filters” or “hints” indicating which kind of Results are extracted. Practically, FeResPost checks whether possible extracted Results contain one of the Strings provided as argument. For example, that the Request “Stress Tensor” matches several Results:
“Stress Tensor”,
“Stress Tensor (RI)”,
“Stress Tensor (MP)”.
On the other hand, the request “Stress Tensor (RI)” matches only “Stress Tensor (RI)”, and not “Stress Tensor” or “Stress Tensor (MP)”.
The other arguments are optional and correspond to the specification of target entities for which Results are read. Actually, the reading operation from an XDB combines the reading and some of the extraction operations described in section I.4.3. For example:
The fifth argument can be a ResKeyList object. Then the Results are extracted on the keys of the ResKeyList object.
The fifth argument can be a Result object. Then the Results are extracted on the keys of the Result object.
Extractions can be performed on Groups. Then one specifies the target by a “Method” String argument and a “GrpTarget” Group argument. The possible values of the “Method” argument are listed in Table I.4.6 of section I.4.3.1. (Description of “extractResultOnEntities” method in the Result class.) When Results are extracted on Groups, one can also specify a list of layers for which values are extracted. This argument is optional. (See below.)
One can also specify a list of layers by providing a parameter which is an Array of String or Integer values. Note however that the filtering on layers is done only when Results for which several layers can be read. For example, this parameter does not influence the reading of MPC Forces, Shell Forces...
One can also specify a list of sub-layers by providing a parameter which is an Array of String or Integer values. Note that this last parameter influences only the reading of laminate stresses or strains. The reading of solid or shell element stresses and strains is not affected by this parameter.
If only four parameters are provided in the call to “getAttachmentResults” method, all the pairs of key-values found in the XDB file are inserted in the list of returned Results.
Only lists below the list of valid calls to “getAttachmentResults”:
h=db.getAttachmentResults(xdbName,lcName,scNames,resNames, method,grpTarget[,layers[,subLayers]]) h=db.getAttachmentResults(xdbName,lcName,scNames,resNames, resTarget) h=db.getAttachmentResults(xdbName,lcName,scNames,resNames, rklTarget) h=db.getAttachmentResults(xdbName,lcName,scNames,resNames [,layers[,subLayers]])
When Results are extracted from an XDB attachment on a Group, the “Method” argument may influence the efficiency of Results extraction. When possible, a real random access is performed, otherwise, entire tables must be read to ensure that all eligible Result values are loaded. For example:
For element Results like element stresses or element forces the “Elements”, “ElemCenters”, “ElemCorners”, “ElemNodes”, “MPCs” and “MPCNodes” extraction methods allow the use of a random access algorithm. On the other hand, the “Nodes” and “NodesOnly” methods are associated to an algorithm that sweeps sequentially the entire corresponding Result tables of XDB file.
For nodal Results, the efficient extraction methods are “Nodes”, “ElemNodes”, “MPCNodes” and “NodesOnly”. They allow the use of a random access algorithm for the extraction of values from each suitable table.
It is the responsibility of the post-processing programmer to try to provide the arguments in order to select the most efficient algorithm for Results extraction.
Note that “Grid Point Forces” are always sorted by nodes. This is true for the applied loads, the MPC/SPC forces and moments, as well as for the internal forces and moments. (Even though these last contain forces by elements and nodes.) This mean that for the selection of extraction algorithm, “Grid Point Forces” should always be considered as nodal Results.
As several Result types, and sub-case names can be given as argument to “getAttachmentResults” method, this method can return several Results. This is why Results are returned in a Hash:
The Hash keys are Array of three Strings corresponding to the name of the load case, the name of the sub-case, and the Result type name respectively.
The Hash values are the Results.
For example, the list of extracted Result sizes can be printed with the following statements:
h=db.getAttachmentResults(xdbFileName,lcName,scNames,resNames,"Nodes",grp)
h.each do |id,res|
lcName=id[0]
scName=id[1]
resName=id[2]
size=res.Size
STDOUT.printf("%s - %s - %s : %d\n",lcName,scName,resName,size)
#~ Util::printRes(STDOUT,"brol",res)
end
The method “getAttachmentResultsCombili” is used to extract linear combinations of elementary Results found in one or several XDB files. As for method “getAttachmentResults” the Results are directly returned by the method to the caller. They are not inserted in the DataBase from which the method is called. This method is more or less a combination of the methods “getAttachmentResults” and “buildLoadCasesCombili” of the generic DataBase class.
Practically, the main difference between “getAttachmentResults” and “getAttachmentResultsCombili” is that the first argument is no longer an Xdb file name. This argument is removed. Instead, one provides a “Combili” argument that describes the linear combination corresponding to extracted Results. This “Combili” argument is the second argument. The first argument is the “LcName” argument corresponding to the load case name attributed to the generated Results. This load case name is unsupposed to correspond to any load case name found in the attached XDB file(s).
The method has minimum four arguments:
A String corresponding to the name of the load case for which Results are read.
A “Combili” Array containing the description of the linear combination of elementary load case Results. The Array is an Array of Arrays. Each secondary Array contains three elements:
A Real value corresponding to the factor in the linear combination.
A String corresponding to the name of the XDB file from which elementary Results are read. This file must have been previously attached to the Nastran DataBase.
A String corresponding to the name of the load case for which Results are extracted.
A String or an Array of Strings corresponding to the names of sub-cases for which Results are read.
A String or an Array of Strings corresponding to the names of Results for which Results are read.
The other arguments are optional and correspond to the specification of target entities for which Results are read. Actually, the reading operation from an XDB combines the reading and some of the extraction operations described in section I.4.3. For example:
The fifth argument can be a ResKeyList object. Then the Results are extracted on the keys of the ResKeyList object.
The fifth argument can be a Result object. Then the Results are extracted on the keys of the Result object.
Extractions can be performed on Groups. Then one specifies the target by a “Method” String argument and a “GrpTarget” Group argument. The possible values of the “Method” argument are listed in section I.4.3.1. (Description of “extractResultOnEntities” method in the Result class.) When Results are extracted on Groups, one can also specify a list of layers for which values are extracted. This argument is optional. (See below.)
One can also specify a list of layers by providing a parameter which is an Array of String or Integer values.
If only four parameters are provided in the call to “getAttachmentResultsCombili” method, all the pairs of key-values found in the XDB file are inserted in the returned Results.
Only lists below the list of valid calls to “getAttachmentResultsCombili”:
h=db.getAttachmentResultsCombili(xdbFileName,lcName,combili, scNames,resNames, method,grpTarget[,layers[,subLayers]]) h=db.getAttachmentResultsCombili(xdbFileName,lcName,combili, scNames,resNames, resTarget) h=db.getAttachmentResultsCombili(xdbFileName,lcName,combili, scNames,resNames, rklTarget) h=db.getAttachmentResultsCombili(xdbFileName,lcName,combili, scNames,resNames [,layers[,subLayers]])
The Hash object returned by the method has a structure identical to the one returned by “getAttachmentResults” and can be manipulated the same way.
The method “importAttachmentResults” is used to read Results from the XDB file. Instead of being returned to the caller in a Hash object, the results are imported into the list of results stored into the Nastran DataBase. The method has four arguments:
db.importAttachmentResults(xdbName,lcName,scNames,resNames)
It is possible to obtain some of the Nastran optimization (SOL200) results from an XDB attachment. Four methods have been defined in NastranDb class:
“getAttachmentDesVarHistory” returns the history of design variables and has three parameters:
“xdbFileName”, a String corresponding to the name of the attached XDB file.
“iSteps”, an Array of integers corresponding to the list of steps for which one wishes to obtain results.
“iDesVarIds”, an array of integers corresponding to the list of design variable IDs for which one wishes to obtained the results.
Parameters 2 and 3 are optional and can be omitted or replaced by a “nil” argument or a void Array. If they are not defined, all the steps or design variables are returned in the results. The method returns a N*3 array. For each line, the three columns correspond to:
The first element is an integer corresponding to the optimization step ID.
The second element is an integer corresponding to identifier of the design variable.
The third element is a float containing the design variable value.
“getAttachmentConstrDefinitions” returns the definition of constraints and has two arguments:
“xdbFileName”, a String corresponding to the name of the attached XDB file.
“iConstrIds”, an array of integers corresponding to the list of constrain IDs.
Parameters 2 is optional and can be omitted or replaced by a “nil” argument. The method returns a N*6 array. For each line, the three columns correspond to:
The first element is an integer corresponding to an internal ID for the considered constrain equation.
The second element is an integer, the Nastran Design Constrain ID.
The third element is an integer corresponding to the internal response ID.
The fourth element is an integer corresponding to RTYPE. (I dot not know what is is.)
The fifth element is an integer corresponding to the LUFLAG. Its value is 1 or 2 (">" or ">").
The sixth element is a float corresponding to the bound.
“getAttachmentConstrHistory” returns the history of constrains and has three parameters:
“xdbFileName”, a String corresponding to the name of the attached XDB file.
“iSteps”, an Array of integers corresponding to the list of steps for which one wishes to obtain results.
“iIRIds”, an array of integers corresponding to the list of internal response IDs for which one wishes to obtained the results.
Parameters 2 and 3 are optional and can be omitted or replaced by a “nil” argument. If they are not defined, all the steps or design responses are returned in the results. The method returns a N*3 array. For each line, the three columns correspond to:
The first element is an integer corresponding to the optimization step ID.
The second element is an integer corresponding to identifier of the design response.
The third element is a float containing the design response value.
“getAttachmentObjectiveHistory” returns the history of constrains and has two parameters:
“xdbFileName”, a String corresponding to the name of the attached XDB file.
“iSteps”, an Array of integers corresponding to the list of steps for which one wishes to obtain results.
Parameter 2 is optional and can be omitted or replaced by a “nil” argument. If it is not defined, all the steps are returned in the results. The method returns a N*3 array. For each line, the three columns correspond to:
The first element is an integer corresponding to the optimization step ID.
The second element is a float corresponding to the value of objective.
The third element is an integer containing the identifier of an internal response.
The fourth element is a float containing the value of the maximum constraint equation (corresponding to the previous internal response).
“getAttachmentDesRespHistory” returns the history of design responses and has three parameters:
“xdbFileName”, a String corresponding to the name of the attached XDB file.
“iSteps”, an Array of integers corresponding to the list of steps for which one wishes to obtain results.
“iDesRespIds”, an array of integers corresponding to the list of design responses IDs for which one wishes to obtained the results.
Parameters 2 and 3 are optional and can be omitted or replaced by a “nil” argument. If they are not defined, all the steps or design variables are returned in the results. The method returns a N*3 array. For each line, the three columns correspond to:
The first element is an integer corresponding to the optimization step ID.
The second element is an integer corresponding to identifier of the design response.
The third element is a float containing the design response value.
So far, the reading of optimization results is experimental and might be changed in future version.
In order to reduce the number of accesses to disk, it may be useful to store some of the blocks read from binary result files into memory. FeResPost provides an algorithm that allows to store the blocks most recently read for later usage. Two singleton methods of the “NastranDb” class allow the to tune the capacity of the buffer area:
“setStorageBufferMaxCapacity” sets the capacity of storage. The method has one arguments: a real value containing the size in Megabytes of the buffer.
“getStorageBufferMaxCapacity” returns the storage buffer current total capacity. The returned value is a real that corresponds to the capacity in Megabytes of the buffer. The method has no argument.
Note that all buffers are now common to all the methods that provide random access to XDB result files. In particular, the method is used in management of the binary file access for XDB attachment or reading. This means that if one Result file attached to one DataBase is more used, the storage will contain a majority of buffers for this Result file and progressively delete the other buffers.
The default capacity for storage buffer is 0Mb. Note that the two methods described above can be called from any class derived from the generic “DataBase” class.
So far, the XDB access methods that have been described allow the extraction of Results only when the corresponding programming has been done in FeResPost source code. Sometimes, this limitation can be frustrating. For that reason, several methods allowing a “low level” or “raw access” to XDB content have been added.
Before listing these methods, one gives some information about the XDB content:
The XDB file is a binary file divided in pages. Each page has a fixed size specified by a given number of words. (This number of words per page is given in the file by the first word of the file.) A word may correspond to 4 or 8 bytes depending whether the XDB file is output in single or double precision.
The XDB file contains different tables corresponding to finite element model, results,... A “dictionnary” allows to identify and retrieve the different tables stored in an XDB file. In FeResPost, each XDB table is identified with a “ String-Integer key”:
The String corresponds to the type of the table. (For example “FBARR” for the Real CBAR element forces.)
As several tables of the same type can be defined in an XDB file, FeResPost also uses an integer index that allows to retrieve the right one.
Each table contains fields that can be distributed into several pages. A field corresponds for example to the forces and moments on one CBAR element, and for a given load case and sub-case. The naming conventions for the table types are given in MSC.Access Manual [Nas05]. The dictionnary keys allow to retrieve information from the dictionnary that can be used to retrieve the table content. This information is given in an Array of 22 integers that correspond for example to
The index of the first page containing the table,
The index of the last page of the table,
The size of the fields in the table (15th element of the table, or element of index 14 when the indices numbering starts with 0),
The number of fields,
The minimum and maximum key IDs,
The number of pages of the table...
(For the reading operations, one generally needs the field size.) You may find more information on the meaning of these 22 integers in MSC.Access Manual [Nas05]. The access to dictionnary is done by calling “getAttachmentDictKeys” and “getAttachmentDictionnary” methods.
When results associated to elements are read from an XDB file, the values are associated to a key that corresponds to the element ID. However, this integer does not correspond to the Nastran integer ID of the element. Instead, there is in the XDB file, an “EQEXINE” table that contains the correspondence between the XDB IDs and the Nastran element IDs:
The first argument of the method is the Access element type which does not correspond to the Nastran element type. A table of correspondence between the XDB Access element types and Nastran element types is given in section “Differences from MSC.Nastran” (sub-section of “BLOCK DATA DESCRIPTIONS”) of the MSC.Access manual [Nas05]. Part of the Access element IDs is given in the source code in method “xdb::getAccessType” (File “NASTRAN/xdb/xdb_equiv.cpp”).
The second argument of the method is the XDB element ID. For each type of element, Nastran generates a sequential XDB numbering starting at 1. The “EQEXINE” table allows to retrieve the corresponding Nastran element ID.
Method “getAttachmentElementExtId” allows to retrieve the Nastran element ID, if you know the type of the element, and its internal ID. The type of the element is the “MSC.Access Element Type” associated to XDB file format. The numbering of element types can be found in [Nas05].
Similarly, the XDB file also contains an “EQEXING” table that allows to retrieve node information. The Access internal node ID numbering starts at 1 and is also sequential. Each node internal ID is associated to three “external” integers:
The Nastran “external” ID of the node that appears in the GRID card definition.
The node type is always “1” in the tests we have done. (We presume it corresponds to usual Nastran GRIDs.)
The Analysis Coordinate System of the GRID. This information is useful as it allows to associate the vectorial results components to a coordinate system.
Method “getAttachmentNodeInfo” is used to retrieve this information when reading nodal results.
The ‘NastranDb” class methods that give a “raw” access to XDB attachment content are:
“getAttachmentElementExtId” that allows to retrieve an element external ID if one knows its “XDB type” and its “XDB internal ID”. The method has three arguments:
A String containing the name of the attachment file,
An integer corresponding to the XDB element type,
An integer corresponding to the XDB internal ID of the element.
The method returns the integer Nastran external ID.
“getAttachmentNodeInfo” has two arguments corresponding to the attachment file name and the node XDB internal ID. It returns an Array of three integers corresponding to the external ID, type and ACID.
“getAttachmentDictKeys” has one String argument corresponding the XDB file name. It returns an Array of two element Arrays. Each of these two element Arrays corresponds to a dictionnary key identified by a String and an integer ID. (See the explanation above.)
“getAttachmentDictionnary” has one String argument corresponding the XDB file name. It returns a “Hash” object that associates dictionnary keys (Arrays of two elements, String and integer) to Arrays of 22 integer elements containing information on the corresponding table.
“each_xdbRaw” is the iterator that allows to retrieve the information from an XDB table. Iterator “each_xdbRaw” has three arguments:
A String containing the name of XDB file attachment.
An Array of two elements (String and integer) corresponding to the dictionnary key ID, and identifying the table on which one iterates.
A String that specifies the translation of the words that are read for each field. Each character of the String corresponds to translation of one word or the production of one value. The correspondence is as explained in Table III.1.3.
An example of call to the iterator follows:
db.each_xdbRaw(xdbFileName,["SUBCASES",0],"iiiiiiii") do |tab|
puts tab
end
The reader must read the examples to better understand the use of this iterator. The examples are discussed in section IV.2.8.
“each_xdbRaw” iterator works fine when the types into which XDB binary data are known a priori. This is not always the case however. Sometimes, the examination of data is needed to determine whether a parameter is a real or a string, or a parameter can be optional. Therefore, is can be interesting to separate the reading of binary data from its interpretation. Iterator “each_xdbBinRaw” iterates on an XDB table and returns each item in a String containing binary data. Iterator has two or three arguments:
A String containing the name of XDB file attachment.
An Array of two elements (String and integer) corresponding to the dictionnary key ID, and identifying the table on which one iterates.
An optional Boolean “BAutoSwap” parameter specifying whether the iterator swaps the endianness if the the endianness of XDB file does not match the one of the machine on which FeResPost is run. The default value of this parameter is true.
The interpreation of binary data is meant to be done by calling “binDataToValues” singleton method of NastranDb class defined below. An example of call to the iterator follows:
db.each_xdbBinRaw(xdbFileName,["SUBCASES",0]) do |str|
...
end
NastranDb class also defines the “binDataToValues”singleton method for interpretation of binary data produced by “each_xdbBinRaw” iterator. The method has four arguments:
A String containing the binary data.
An integer corresponding to the size of words in bytes (4 or 8 bytes per word).
A String specifying how binary data are translated into VALUES. Each character of the String corresponds to translation of one word or the production of one value. The correspondence is as explained in Table III.1.3.
An integer specifying the endianness swapping policy followed by the translator. Four values are possible:
value 0 means that binary words are never swapped befor interpretation.
value 1 means that binary words are swapped only if translated to a String.
value 2 means that binary words are swapped only if translated to something else than a String.
value 3 means that binary words are always swapped.
The reason why one needs to specify a swapping policy is that “binDataToValues” is not aware of the XDB file from which the binary data have been extracted. The distinction between String and other values results from the fact that Nastran swaps the bytes of integer and real values, but not the bytes of Strings.
We recomment to set policy to 0 if no swap is needed and to 1 if a swap is needed. (See the example in section IV.2.8.
Note that binary String produced by “each_xdbBinRaw” iterator can also be interpreted by the “unpack” method of Ruby Strings or equivalent capabilities of other programming languages.
| Char | Conversion Action |
| “i” or “l” | One word is converted to a single precision integer |
| “u” | One word is converted to a single precision unsigned integer |
| “I” or “L” | 8 bytes (one or two words) are converted to a long long (8 bytes integer) |
| “U” | 8 bytes (one or two words) are converted to an unsigned long long (8 bytes unsigned integer) |
| “f” or “d” | One word is converted to a float (single precision real value) |
| “F” or “D” | 8 bytes (one or two words) are converted to a double (double precision real value) |
| “s” | One word is converted to a String |
| “S” | 8 bytes (one or two words) are converted to a String |
| “x” | One word is skipped and a nil value is generated |
| “X” | 8 bytes (one or two words) are skipped and a nil value is generated |
| “y” | One word is skipped and no value is generated |
| “Y” | 8 bytes (one or two words) are skipped no value is generated |
Since version 4.5.0 of FeResPost, it is possible to read results from Nastran HDF5 files. The operation is done in several steps:
The reading of HDF files is possible only after the HDF5 shared library is loaded into FeResPost. This is done by calling method “Post.loadHdf5Library” described in section I.6.11.
The HDF file is attached to the DataBase and its content (lists of load cases, sub-cases and Results) is identified. Several methods give access to this information.
The Results that are needed are then read from the file (into a Nastran Database, or returned into a Hash).
The different methods called to perform these operations are described in the following sub-sections.
The “readHdf” method is used to read Results into the DataBase from an “hdf” file generated by Nastran. (Only Results can be read from a Nastran “hdf” file.) The method has up to four arguments:
A String argument that corresponds to the name of the file from which Results are read.
A String or an Array of Strings corresponding to the names of load cases for which Results are imported into the DataBase. If the Array is void or the parameter is omitted, all load cases in hdf result files are considered when results are read.
A String or an Array of Strings corresponding to the names of subcases for which Results are imported into the DataBase. If the Array is void or the parameter is omitted, all sub-cases in hdf result files are considered when results are read.
A String or an Array of Strings corresponding to the identifiers of Results for which Results are imported into the DataBase. If the Array is void or the parameter is omitted, all Results of hdf result files are considered when results are read.
All parameters, except the first one, can be omitted. Then the method assumes that a void Array has been passed as argument.
This method is a kind of wrapper to several methods described above. If necessary, FeResPost attaches the HDF file, imports the results into the database, and closes the attachment. If the HDF is alread attached, no attachment/detachment is done.
The “readHdf2H” method is used to read Results from an “hdf” file generated by Nastran and return them into an Hash object. Arguments are the same as those of “readHdf” method.
The method “attachHdf” is used to attach an HDF file to the Nastran DataBase. This method has up one argument: a String containing the name of the HDF file. (Full path name must be provided.)
Several other methods are used to manage the Hdf attachments to a DataBase:
“detachHdf” is used to delete an HDF attachment. The method has one String argument corresponding to the name of the HDF file. (Same argument as the one used to attach the file.)
“removeAllHdfAttachments” removes all the HDF file attachments to a DataBase. This method has no argument.
“getNbrHdfAttachments” has no argument and returns the number of HDF files attached to the DataBase.
“getHdfAttachmentNames” has no argument and returns an Array of Strings containing the list of HDF files attached to the DataBase.
“checkHdfAttachmentExists” has one String argument containing the HDF file name, and returns “True” if the HDF file is Attached to the DataBase, and “False” otherwise.
The following methods extract information related to the Results stored in an HDF file attached to the DataBase:
“getHdfAttachmentLcInfos” returns information on load cases and sub-cases of Results found in the attached Hdf file. The information is returned in an Array. (More information about the content of this Array is given in the description of method“getXdbLcInfos”.)
“getHdfAttachmentNbrLoadCases” returns the number of load cases found in an HDF file.
“getHdfAttachmentLcNames” returns an Array of Strings corresponding to the load case names found in the HDF file.
“getHdfAttachmentLcScNames” returns an Array containing two elements. The first element is an Array of String containing the load case names found in the HDF file. The second element is an Array of String containing the sub-case names found in the HDF file.
“getHdfAttachmentLcScResNames” returns an Array of three elements. Each element is an Array of Strings. The first element is the list of load case names. The second element is the list of sub-case names. The last element is the list of Result names.
All these methods have a single String argument containing the name of the HDF file that must have been previously attached to the DataBase. On the other hand, the following methods have one or two arguments:
“getHdfAttachmentNbrSubCases” returns the number of sub-cases found in an HDF file.
“getHdfAttachmentScNames” returns an Array of Strings corresponding to the sub-case names found in the HDF file.
“getAttachmentNbrResults” returns the number of Result names identified in the HDF attached file.
“getHdfAttachmentResIds” returns an Array of Integers corresponding to the identifiers of the Results found in the HDF file.
“getHdfAttachmentResNames” returns an Array of Strings corresponding to the names of the Results found in the HDF file.
The first argument is the name of the HDF file that must have been previously attached to the DataBase. The second argument is optional and corresponds to the name of a load case found in the attached HDF file. If the argument is not provided, all the load cases are investigated to build the list of sub-cases or Result names or IDs. If the argument is provided, only the sub-cases or Results of the corresponding load case are considered. If the provided load case does not exist in HDF attachment an error message is issued.
Two methods are used to extract results from Nastran HDF files:
Method “readHdfAttachmentResults” is used to read Results from the HDF file. Results are stored in the NastranDb object.
Method “getHdfAttachmentResults” is used to read Results from the HDF file. Results are returned in a Hash object.
The two methods have up to four arguments:
A String corresponding to the name of HDF file attachment from which Results are read. (This file must have been previously attached to the DataBase.)
A String or an Array of Strings corresponding to the names of load cases for which Results are read.
A String or an Array of Strings corresponding to the names of sub-cases for which Results are read.
A String or an Array of Strings corresponding to the names of Results for which Results are read.
One lists below valid calls to “getHdfAttachmentResults”:
h=db.getHdfAttachmentResults(hdfName,lcNames,scNames,resNames) h=db.getHdfAttachmentResults(hdfName,lcNames,scNames) h=db.getHdfAttachmentResults(hdfName,lcNames) h=db.getHdfAttachmentResults(hdfName)
Similar calls work for “readHdfAttachmentResults” method:
db.readHdfAttachmentResults(hdfName,lcNames,scNames,resNames) db.readHdfAttachmentResults(hdfName,lcNames,scNames) db.readHdfAttachmentResults(hdfName,lcNames) db.readHdfAttachmentResults(hdfName)
When one of the “lcNames”, “scNames” or “resNames” is missing, nil or an empty Array, all the load cases, sub-cases or result types are read. “getHdfAttachmentResults” method is very similar to the “getAttachmentResults” method used to extract Results from Nastran XDB result files.
Several methods can be used to obtain a “raw” access to Nastran HDF Datasets:
“getHdfAttachmentDataSets” produces a list of Dataset paths in a given HDF attachment. The method has one String argument corresponding to the path to attachment. It return an Array of Strings, each String corresponding to the path to corresponding Dataset in HDF file.
“getHdfAttachmentCompoundMemberNames” returns an Array of Strings corresponding to the column names of a Compound Dataset. The Dataset is referred to by the two String arguments correspond to attachment path and Dataset path respectively. (Of course the Dataset referred to must be of “Compound” type for the method to work.)
“getHdfAttachmentDataSetNbrItems” returns the number of items (or lines) in a Dataset. The Dataset is referred to by the two String arguments correspond to attachment path and Dataset path respectively.
“each_hdfAttachmentNasSetItem” iterates on a Compound Dataset items. The method has 2 or 4 arguments:
“HdfPath”, a String correspond to the path associated to HDF attachment.
“DataSetPath”, a String correspond to the Dataset path in HDF attachment.
“IPosMin”, the index of the first item to be iterated to in DataSet.
“IPosMax”, the index of the last item to be iterated to in DataSet.
For each item found in Dataset, the iterator returns an Array containing the values in each column of the corresponding Compound object. If arguments “IPosMin” and “IPosMax” are omitted, one iterates on all the items of the Dataset.
“getHdfAttachmentDataSet” returns an Array corresponding to items read from a Dataset. Each element of the Array corresponds to an Array that contains the values of the corresponding item. (=Array returned by “each_hdfAttachmentNasSetItem” iterator.) The method has the same arguments as the iterator.
Remarks:
The two last methods are no general HDF5 Compound Dataset reader. They have been tested for Nastran Datasets and can only be expected to work for Nastran HDF5 files.
User does not need to specify how the items being read must be translated into objects of the language he is using, as has been done with WDB raw iterators in section III.1.1.10.7. This is because each HDF Compound Dataseets also contains a description of data storage.
The method “writeGmshMesh” defined in DataBase Class exports nodes, elements and RBEs into the mesh file. RBEs are exported with a negative integer ID. The three tags attributed to the elements are the property ID (twice) and the laminate ID. This means that the three tags have sometimes the same value.
A first group of iterators iterate on finite element entities of the finite element model stored in the DataBase.
“each_coordSysId” iterates on the integer identifiers of coordinate systems.
“each_elemId” iterates on the integer identifiers of elements.
“each_rbeId” iterates on the integer identifiers of rigid body elements.
“each_mpcId” iterates on the integer identifiers of MPC and MPCADD cards.
“each_propertyId” iterates on the integer identifiers of properties.
“each_materialId” iterates on the integer identifiers of materials.
The elements produced by the iterator are single integers. Each of these iterators has 0, 1 or 2 arguments. The two optional arguments are the integer bounds considered for the iteration: “IdMin” and “IdMax”.
Two iterators loop on the nodes defining an element:
These two iterators have one integer argument corresponding to the index of the element. They iterate on the integer indices of nodes.
Iterator “each_xdbRaw” is discussed in section III.1.1.10.7. Iterator “each_bdfCard’ allows to read the content of one (or several) BDF file(s), without trying to import the corresponding FEM entities in a NastranDb database. This is a singleton method, which means that the method is to be called directly from NastranDb class. The arguments of the method are the same as those of “readBdf” method described in section III.1.1.1:
A String containing the name of the main Nastran Bulk Data File.
An Array of Strings containing the list of directories in which files specified by “include” statements shall be searched. Its default value is a void Array.
The name of an extension that may be added to the file names specified in include statements. Its default value is a void String. (This argument corresponds to the jidtype in Nastran.)
A Hash with String keys and values corresponding to the list of “symbols” that can be used in “include” statements in the Bulk Data Files. The default value is a void Hash.
A Logical that specifies verbosity for the scanning of the Nastran Bulk Data File. Its default value is “false”. This parameter is redundant with “setVerbosityLevel” of “Post” Module: to set the parameter to “true” is equivalent to set “Post” verbosity level to 1.
A Logical that specifies whether the file contains only Bulk Data Section lines. Its default value is “false”. If the parameter is “true”, the “BEGIN BULK” and “ENDDATA” lines are ignored, and all the input lines, except comments, are interpreted. (See also the remarks below.)
For example, the iterator can be used as follows:
NastranDb.each_bdfCard("../../MODEL/MAINS/unit_xyz.bdf") do |crd|
puts crd
end
Several other methods allow to obtain model information.
“getRbeNodes” returns the number of dependent and independent nodes defining an RBE. The argument of the method is the RBE integer ID.
“getRbeDependentNodes” returns the number of dependent nodes of an RBE. The argument of the method is the RBE integer ID.
“getRbeIndependentNodes” returns the number of independent nodes of an RBE. The argument of the method is the RBE integer ID.
“getMpcNodes” returns the number of dependent and independent nodes defining an MPC. The argument of the method is the MPC integer ID.
“getMpcDependentNodes” returns the number of dependent nodes of an MPC. The argument of the method is the MPC integer ID.
“getMpcIndependentNodes” returns the number of independent nodes of an MPC. The argument of the method is the MPC integer ID.
“getElementPropertyId” has an integer argument corresponding to the element ID and returns the corresponding property ID.
“getNodeRcId” has an integer argument corresponding to the node ID and returns the corresponding reference coordinate system ID.
“getNodeAcId” has an integer argument corresponding to the node ID and returns the corresponding analysis coordinate system ID.
“getNodeCoords” returns the coordinates of a node. This method has one or two arguments:
The first argument is an integer corresponding to the node ID.
The second argument is an integer or a string that corresponds to the coordinate system in which the coordinates are expressed. The argument is an integer, or the “AsIs” string. Note that if the argument is missing, the “AsIs” coordinate system is considered.
Two attribute “getters” allow to access information in the model:
“NbrRbes” returns the number of rigid body elements stored in finite element model. This method has no argument.
“NbrMpcs” returns the number of MPC/MPCADD cards stored finite element model. This method has no argument.
When a Result object is read from an “op2” or an “xdb” file, integer and/or real identifiers are associated to the object. These identifiers depend on the solution sequence to which the Results correspond:
For SOL 101: IntId[0] corresponds to the sub-case identifier, and IntId[1] is the load set number.
For SOL 103: IntId[0] corresponds to the sub-case identifier, and IntId[1] is the mode number. RealId[0] is the real eigenvalue. The corresponding eigen-frequency is given by . (Note however that this eigen-frequency is left undefined for the Grid Point Forces.)
For SOL 105: IntId[0] corresponds to the sub-case identifier, and IntId[1] is the mode number. RealId[0] is the real eigenvalue, corresponding to the critical load. (Note however that this critical load is left undefined for the Grid Point Forces.)
For SOL 106 and SOL 400: IntId[0] corresponds to the sub-case identifier, and IntId[1] corresponds to the step index in the sub-case. RealId[0] is the value of the continuation parameter for which the Results have been saved in the Result file.
For SOL 108 and SOL 111 Results, the IntId[0] corresponds to the frequency output integer ID, and RealId[0] corresponds to the frequency value. The same is true for the PSD and CRMS random analysis outputs, which are saved for each frequency output.
The “load case name” identifier associated to read or accessed results correspond to the “SUBTITLE” associated to the SUBCASE defined in Nastran data file. If this SUBTITLE is not define, the SUBCASE ID is used to generate a default load case identifier as follows:
lcName="Load Case "+ID
The subcase names are automatically generated by FeResPost when the Results are read from output files. Table III.1.5 lists possible subcase names generated by FeResPost when Nastran Results are read from OP2, XDB or HDF files. The integer and real values associated to the Results for each Nastran solution type are listed in Table III.1.4.
Finally, the results found in the op2 file are presented by blocks corresponding to the different “result element types”. Unfortunately, those element types do not correspond exactly to the element bdf cards presented in section III.1.1.1. The supported result element types are: “ROD”, “BEAM”, “TUBE”, “SHEAR”, “CONROD”, “ELAS1”, “ELAS2”, “ELAS3”, “ELAS4”, “DAMP1”, “DAMP2”, “DAMP3”, “DAMP4”, “VISC”, “MASS1”, “MASS2”, “MASS3”, “MASS4”, “CONM1”, “CONM2”, “PLOTEL”, “QUAD4”, “BAR”, “GAP”, “TETRA”, “BUSH1D”, “QUAD8”, “HEXA”, “PENTA”, “BEND”, “TRIAR”, “TRIA3”, “TRIA6”, “QUADR”, “TETRANL”, “GAPNL”, “TUBENL”, “TRIA3NL”, “RODNL”, “QUAD4NL”, “PENTANL”, “CONRODNL”, “HEXANL”, “BEAMNL”, “QUAD4LC”, “QUAD8LC”, “TRIA3LC”, “TRIA6LC”, “BUSH”, “FAST”, “QUAD144”, “QUADRNL”, “TRIARNL”, “ELAS1NL”, “ELAS3NL”, “BUSHNL”, “QUADRLC” and “TRIARLC”. (More information on the result element types can be found in [Rey04].)
Here again, some of the element result types can be disabled or enabled (section III.1.1.1). The arguments given to the enabling or disabling methods correspond to a String object, or an Array of Strings, the values of Strings corresponding to some of the Result element types given just above.
The negative node values corresponding to Results on specific Nastran elements are summarized in Table III.1.6. (This Table is a complement to Table I.4.2.) These keys can be used when Results are read from “OP2” or “XDB” files. Note that the “CbarGrdA” and “CbarGrdB” are used only to associate values to CBAR end nodes when the definition of CBAR element has not been found in the DataBase.
| For Nastran CSHEAR element | |
| "F4to1" | -201 |
| "F2to1" | -202 |
| "F1to2" | -203 |
| "F3to2" | -204 |
| "F2to3" | -205 |
| "F4to3" | -206 |
| "F3to4" | -207 |
| "F1to4" | -208 |
| "kickOn1" | -211 |
| "kickOn2" | -212 |
| "kickOn3" | -213 |
| "kickOn4" | -214 |
| "shear12" | -221 |
| "shear23" | -222 |
| "shear34" | -223 |
| "shear41" | -224 |
For Nastran CBEAM element (or CBAR element with intermediate stations)
| |
| "CbeamSt01" to "CbeamSt40" | -101 to -140 |
| For Nastran CBAR element
| |
| "CbarGrdA" | -151 |
| "CbarGrdB" | -152 |
The correspondence between the Nastran output requests and the DMAP data blocks written in the “op2” file is given in Tables III.1.7 to III.1.16. Note that in all the examples presented in Part IV, the results are printed in the “op2” file with “SORT1” option. This means that no test has been done with “SORT2” option.
| Nastran | “op2” | Generated |
| Statement | Data Block | Result |
| DISPL | OUG | “Displacements, Translational” “Displacements, Rotational” “Displacements, Scalar” |
| VELO | OUG | “Velocities, Translational” “Velocities, Rotational” “Velocities, Scalar” |
| ACCEL | OUG | “Accelerations, Translational” “Accelerations, Rotational” “Accelerations, Scalar” |
| Nastran | “op2” | Generated |
| Statement | Data Block | Result |
| GPFORCES | OGF | “Grid Point Forces, Internal Forces” “Grid Point Forces, Internal Moments” “Grid Point Forces, MPC Forces” (2) “Grid Point Forces, MPC Moments” (2) “Grid Point Forces, MPC Internal Forces” (4) “Grid Point Forces, MPC Internal Moments” (4) “Grid Point Forces, SPC Forces” (2) “Grid Point Forces, SPC Moments” (2) “Grid Point Forces, Applied Forces” (2) “Grid Point Forces, Applied Moments” (2) |
| Nastran | “op2” | Generated |
| Statement | Data Block | Result |
| STRAIN | OES | “Strain Tensor” (5, 2) “Beam Axial Strain for Axial Loads” “Beam Axial Strain for Bending Loads” “Beam Axial Strain for Total Loads” (9) “Beam Shear Strain for Torsion Loads” “Beam Deformations” (15) “Beam Velocities” (15) “Beam Stations” (18) “Gap Forces” (16) “Gap Deformations” (16) “Gap Slips” (16) “Spring Scalar Strain” “Bush Forces Strain Tensor” (13 and 14) “Bush Moments Strain Tensor” (13 and 14) “Bush Plastic Strain” (13 and 14) “Curvature Tensor” (5, 8) “Shear Panel Strain, Max” “Shear Panel Strain, Average” |
| Nastran | “op2” | Generated |
| Statement | Data Block | Result |
| STRESS | OES | “Stress Tensor” (1 in section III.1.2.2) “Beam Axial Stress for Axial Loads” “Beam Axial Stress for Bending Loads” “Beam Axial Stress for Total Loads” (9) “Beam Shear Stress for Torsion Loads” “Beam Forces” (13 and 14) “Beam Moments” (13 and 14) “Beam Deformations” (15) “Beam Velocities” (15) “Beam Stations” (18) “Gap Forces” (16) “Gap Deformations” (16) “Gap Slips” (16) “Spring Scalar Stress” “Bush Forces Stress Tensor” (13 and 14) “Bush Moments Stress Tensor” (13 and 14) “Bush Stress, Axial” (15) “Bush Strain, Axial” (15) “Bush Plastic Strain” (15) “Shear Panel Stress, Max” “Shear Panel Stress, Average” |
| Nastran | “op2” | Generated |
| Statement | Data Block | Result |
| NLSTRESS | OES | “Nonlinear Stress Tensor” (6) “Nonlinear Strain Tensor” (6) “Nonlinear Effective Plastic Strain” (6) “Nonlinear Effective Creep Strain” (6) “Nonlinear Spring Scalar Strain” “Nonlinear Spring Scalar Stress” “Nonlinear Beam Axial Strain for Axial Loads” “Nonlinear Beam Axial Stress for Axial Loads” “Nonlinear Beam Axial Strain for Total Loads” “Nonlinear Beam Axial Stress for Total Loads” “Nonlinear Beam Forces” “Nonlinear Beam Moments” “Beam Stations” (18) “Nonlinear Bush Forces Stress Tensor” (13 and 14) “Nonlinear Bush Moments Stress Tensor” (13 and 14) “Nonlinear Bush Forces Strain Tensor” (13 and 14) “Nonlinear Bush Moments Strain Tensor” (13 and 14) “Nonlinear Gap Forces” (16) “Nonlinear Gap Deformations” (16) “Nonlinear Gap Slips” (16) |
| Nastran | “op2” | Generated |
| Statement | Data Block | Result |
| FORCE (1, 15) | OEF | “Shell Forces” “Shell Moments” (7) _______________________________________________ “Beam Forces” (10, 11,12) “Beam Moments” (10, 11,12) “Beam Warping Torque” “Beam Deformations” “Beam Velocities” “Beam Stations” (18) “Gap Forces” (16) “Gap Deformations” (16) “Gap Slips” (16) “Spring Scalar Forces” “Bush Plastic Strain” |
| Nastran | “op2” | Generated |
| Statement | Data Block | Result |
| ESE | OEE | “Element Strain Energy” “Element Strain Energy (Density)” “Element Strain Energy (Percent of Total)” |
| EKE | OEE | “Element Kinetic Energy” “Element Kinetic Energy (Density)” “Element Kinetic Energy (Percent of Total)” |
| EDE | OEE | “Element Energy Loss” “Element Energy Loss (Density)” “Element Energy Loss (Percent of Total)” |
| Nastran | “op2” | Generated |
| Statement | Data Block | Result |
| TEMPERATURE | OUG | “Temperature” |
| FLUX | OEF | “Temperature Gradient” |
| FLUX | OEF | “Conductive Heat Flux” |
One can make a few remarks about the information given in Tables III.1.7 to III.1.16:
The Nastran “CELASi” and “CDAMPi” elements produce scalar forces or moments that are stored in “Beam Scalar Forces” Results.
“Applied Loads” are available both with the “OLOAD” and “GPFORCE” Nastran statements. A similar remark can be done for “MPC Forces” and “SPC Forces”.
When forces or moments corresponding to “Applied Loads”, “MPC Forces” or “SPC Forces” are read by FeresPost, key-values pairs are inserted only when at least one of the components is not zero. This has been done to avoid the creation of Result objects filled with a lot of zero values.
When the option “RIGID=LAGR” is activated, the contributions of rigid body elements and MPCs are included in “Grid Point Forces, MPC Forces” and “Grid Point Forces, MPC Moments” and not in “Grid Point Forces, Internal Forces” and “Grid Point Forces, Internal Moments”:
For the Results “Grid Point Forces, MPC Forces” and “Grid Point Forces, MPC Moments” The ElemId of each key is set to “NONE”. (These Results are pure nodal Results.)
For the “Grid Point Forces, Internal Forces” and “Grid Point Forces, Internal Moments” Results, The ElementId associated to each vector corresponds to the MPC ID of the RBE element. This means that one must be careful when extracting these Results on Groups of MPCs.
The shear components of strain tensor output by Nastran are the angular deformations: . When these results are imported in a NastranDb, the corresponding components are divided by two in such a way that a “physical” tensor is stored into the NastranDb. The same remark applies for the non-diagonal components of the curvature tensor (shell elements).
The “STRAIN” Nastran output statement with “FIBER” option outputs the strain tensor at Z1 and Z2, but do not produce the curvature tensor.
The Nonlinear stresses and strains are available for CHEXA, CPENTA, CTETRA, CQUAD4 and CTRIA3 elements. Plastic deformation results are produced for non-linear results only.
When shell bending moments are imported from Nastran finite element results, the sign of each component is changed. This has been done to ensure that a positive component of the bending moment results in a positive value of the corresponding stress tensor component on the upper face of the shell. In other words, a positive bending corresponds to tension stress in shell upper face. (See equation II.1.31 for the definition of bending moments tensor components.)
When Nastran shell curvature Results are imported, two modifications are brought to the components:
The signs of all the components are changed,
The shear components of the tensor are divided by two.
This is done because FeResPost considers that positive curvature components correponds to positive strain components in upper face of the shell, and negative components in lower face of the shell. (See equation II.1.32 for the definition of curvature tensor components.)
“Axial Strain” or “Axial Stress” for “Total Loads” and CBAR elements are produced by combined axial loads to bending loads. This has been done to harmonize CBAR Results with CBEAM Results. For CBEAM Results, Stresses or Strains are recovered on the extremities only.
Nastran “BEAM” type elements (CBAR, CBEAM, CBEND,...) do not output vectorial or tensorial forces or moments. Instead, the different components are expressed in different coordinate systems (axial, plane 1 and plane 2). When importing these Results, a conversion into tensorial format is done as follows:
|
|
|
|
Nastran CBUSH elements produce forces and moments corresponding to the loads applied by Grid B of the element to Grid A. By analogy with the what is done for “BEAM” type of elements, one produces “Beam Forces” and “Beam Moments” filled as follows:
|
|
|
|
The choice of considering bush forces and moments as beams is questionable, and we justify this choice as follows:
When grids A and B are not coincident, the definition of CBUSH element axes can be done the same way as for CBEAM elements (Figure III.1.1.a). The vector points from grid A to grid B, and component of force vector is positive when the CBUSH element is in tension, and the analogy between CBUSH element and CBEAM elements perfect, and the tensorial character of CBUSH element forces and moments is obvious.
It is no longer true when the CBUSH orientation is specified with a coordinate system as represented in Figure III.1.1.a. In such a case, component of force vector no longer can be interpreted as a tension in CBUSH element. It is only the force applied by grid B to grid A, and projected on CBUSH coordinate system axis.
CBUSH elements are often used in the modeling of connections. Whatever the type of coordinate system definition, is is always possible to obtain vectorial forces and moments by a contracted multiplication of the vectorial result with a unit vector:
|
|
|
|
This is generally the first operation performed when CBUSH loads are used for the sizing of connections. This also works when connection forces are extracted from CBEAM or CBAR elements.
For CBAR elements, “Beam Forces” are always produced at the center of elements, and “Beam Moments” at the two end nodes. For CBEAM elements, “Beam Forces” and “Beam Moments” can be requested at different stations long the element. A minimum is then the production of outputs at the two ends of the element; Therefore, “Beam Forces” are output at element end nodes, as a minimum. But generally, no “Beam Forces” are output at element centers.
Bush result types for OEF and OES outputs depend on the kind of BUSH elements to which they correspond:
Nastran “CBUSH” elements for linear analyses produce vectorial or tensorial results in OEF and OES blocks.
Nastran “CBUSH” elements for non-linear analyses produce vectorial or tensorial results in OES blocks. No results are produced in OEF blocks.
The element forces and moments are stored in “Beam Forces” and “Beam Moments” tensorial Results.
The result types generated for CFAST elements are the same as for CBUSH elements.
Note that FeResPost cannot determine the CFAST element coordinate system when grids A and B are coincident. This may cause problems when transformation of reference coordinate systems are required. (This is the case when gmsh outputs of results are requested.) Note also that Patran also seems to experience some difficulties to calculate CFAST element axes.
Nastran “CBUSH1D” elements produce scalar results in OEF and OES blocks. By this we means that each type of result has only one single component. However, the scalar force is stored in “Beam Forces” tensorial result. Most components of the tensor are zero:
|
|
No bending moments are produced by “CBUSH1D” elements.
Nastran “CGAP” elements produces various results. These Results are read from OES or OEF data blocks. These Results are tensorial and:
Gap forces results are stored in “Gap Forces” tensorial Result. The value of the axial component is multiplied by “-1.0”, because it is a compression component.
Gap deformations are stored in “Gap Deformations” tensorial Result. Here again the value of the axial component is multiplied by “-1.0”.
“Gap Slips” is identical to “Gap Deformations” except that the axial component is set to “0.0”.
Various Nastran elements refer scalar points instead of grids. Nevertheless, Nastran considers the scalar point as a kind of element rather than as a kind of grid. This is, in our opinion, an unfortunate choice! FeResPost considers SPOINT and EPOINT objects as a peculiar type of GRID. This has implications for the definition of keys when importing Results with from Nastran op2 files. One hopes that this will not lead to problems!
The “Beam Stations” scalar result is produced when stresses, strains or forces are read for CBEAM or CBAR elements:
This Result corresponds to the location of beam load recovery along the 1D element and varies between 0 and 1. It is scalar and has always a real format.
Intermediate stations, differing from 0 or 1, are produced by CBEAM elements, or CBAR elements if associated to a CBARAO card.
Up to 40 intermediate stations are supported by FeResPost. Beyond this value, Beam results are not read. This limit should be sufficient as Nastran Manuals recommend that no more than 6 intermediate stations are defined by CBARAO bulk card, and as CBEAM element allow up to 9 intermediate stations.
The node IDs to which intermediate station values are associated correspond to the “CbeamSt01” to “CbeamSt40” IDs defined in Table III.1.6.
“Nonlinear” outputs may result from various output requests as “NLSTRESS”, “STRESS”, “STRAIN”, “FORCE”... The “Nonlinear” character of Results is more related to the type of Nastran solution than to the output request. For example, Nastran SOL 106 or SOL 400 analyses are likely to produce “Nonlinear” outputs.
This section is more specifically devoted to the composite Results (failure indices). Failure indices can be imported from “op2” files only. The different Results that can be imported from Nastran are summarized in Table III.1.17. One can make a few remarks about the information given in those Tables:
Since version 3.4.2, the stress tensor in plies is produced in “Mid” sub-layer only. This means that the out-of-plane shear stress that Nastran calculates at bottom skin of each ply is displaced at mid-thickness of the ply. This is an approximation. (This out-of-plane shear stress can be used to calculate inter-laminar shear stress in composite.)
A rotation of the out-of-plane shear components is done in such a way that all components are given wrt ply axes. (Nastran outputs these components in laminate axes.)
When Nastran composite strains are read, values are produced for Mid thickness of each ply only. Nothing is produced on ply upper or lower faces.
The remarks done about the conversion of angular shear strain components to tensorial shear strain components are of course also valid for layered strain Results.
Failure indices can be read from “op2” files only. Corresponding Results do not seem to be stored in “xdb” files.
The indices given in Table III.1.17 refer to the remarks above.
Four methods devoted to the enabling or disabling of composite layered Results are defined in the generic “DataBase” class. These methods are presented in section I.1.3.2.
The correspondence between the failure indices read from Nastran “op2” files and Results produced by CLA classes is as in Table III.1.18.
| Nastran Result | CLA criterion ID | section |
| “Composite Failure Index, Tsai-Hill” | “TsaiHill_c” | II.1.10.11 |
| “Composite Failure Index, Tsai-Wu” | “TsaiWu” | II.1.10.14 |
| “Composite Failure Index, Hoffman” | “Hoffman” | II.1.10.16 |
| “Composite Failure Index, Maximum Strain, CompMax” | “MaxStrain” | II.1.10.6 |
| “Composite Failure Index, Interlaminar Shear Stress” | “Ilss” | II.1.10.27 |
When a PCOMP or a PCOMPG property card is translated into a ClaLam object by a call to “getClaDb” method, the value of LAM parameter is not taken into account. This means that the values of this parameter set to “MEM”, “BEND”, “SMEAR” or “SMCORE” is without effect. There is one exception to this rule: the value “SYM” is taken into account in PCOMP property cards. (But not in PCOMPG cards for which this parameter value is illegal.)
Most methods peculiar to the post-processing of Samcef finite element Results and models are defined in class “SamcefDb” that inherits the “DataBase” class. This class is described in section III.2.1.
A “SamcefDb” object can be created by a statement using “new” method like:
db=SamcefDb.new()
Method “initialize” initializes or clears a SamcefDb object. This class is a specialization of the FeResPost “DataBase” class.
Method “readSamcefDat” of the SamcefDb class is used to import the model in a SamcefDb. This function has up to three arguments:
A String object containing the name of the “banque” file from which the model is read. This file should be obtained by a “.sauve banque” command in Bacon. However, it may have been split into several files.
The second argument is a logical value (true or false) specifying whether the Groups defined in the banque file are to be imported too. However, it may be useful not to import the Groups from the banque file if one prefers to import them from a Patran session file (see section I.1.2.1). This argument is optional and its default value is “true”.
A Logical argument specifying the verbosity of the reading operations. Its default value is “false”. This parameter is redundant with “setVerbosityLevel” of “Post” Module: to set the parameter to “true” is equivalent to set “Post” verbosity level to 1.
The model can be split into several files loaded in a main file by input statements. However, the user should try to be conservative when splitting its model. For example:
The statement begins with keyword “input” or “INPUT”.
It may be followed by a label (“input.label”).
The statement cannot contain comments.
...
Here is a few examples of valid input statements:
input "../SPLIT_1/grids.dat" input "../SPLIT_1/elements.dat" input.beginC "../SPLIT_1/props.dat" input.beginB "../SPLIT_1/geom.dat" input "/home/ferespost/SAM_SPLIT/SPLIT_1/mecano.dat"
Note that for a reason unknown, the “.sauve banque” bacon command outputs the list of abbreviations defined in a database at the end of the banque after a “return” statement. This “return” statement must be removed or commented out if the abbreviations are to be imported in the database by the “readSamcefDat” command.
Finally, Since version 4.5.7 of FeResPost, we have been trying to better support the Samcef input files produced directly by Siemens NX software. This has been done by working with a limited number of example files, and modifying the C++ sources until correct FeResPost reading is obtained. We do not guaranty that all features exported by NX are supported by FeResPost. This means that the reading of a file obtained via the “.sauve banque” Bacon command remains the safest way to read successfully a Samcef model. So, for NX users, our recommendations are:
First attempt the reading of NX output without any modification.
If this fails, revert to the “.sauve banque” approach.
And you will help us to improve FeResPost by providing NX files that FeResPost fails to read.
Note also that the use of non-ASCII characters in Samcef file names, or in the names of directories via which inut files are included should be avoided. (See more details regarding this rule in section III.1.1.1 in Nastran solver reference for more details.)
The “CoordSys” class allows the manipulation of coordinate systems for post-processing purpose. This class is presented in Chapter I.2. One presents below the methods of SamcefDb class devoted to the manipulation of coordinate systems.
The “getCoordSysCopy” method returns a CoordSys object which is a copy of a coordinate system stored in the DataBase. The method has one integer argument which is the index of the coordinate system.
Note that the CoordSys returned by the method may be a “generic” CoordSys as presented in Chapter I.2, or a Samcef frame.
The “addCoordSys” method is used to add a coordinate system to the DataBase. The argument of the method is the CoordSys object. In the DataBase, the object is referenced by its index.
If a coordinate system with the same index already exists in the SamcefDb, it is replaced by the new coordinate system. In that case, the user is responsible for all the modifications involved in the finite element model by the possible modification of the SamcefDb coordinate system. Therefore, it is considered as a good practice not to modify a coordinate involved in the finite element model definition.
Note that the coordinate system index must be a strictly positive integer. Also, the CoordSys inserted by the method may be a “generic” CoordSys as presented in Chapter I.2, or a Samcef frame.
makeAllCoordSysWrt0 method updates the definition wrt 0 (most basic coordinate system) of all the coordinate systems stored in a NastranDB. This operation is necessary when a coordinate system of the NastranDB has been modified, because the definitions of other coordinate systems wrt 0 may be affected.
The list of “SamcefDb” methods returning Groups defined by association is given below:
“getElementsAssociatedToNodes”. (See description in “NastranDb” class.)
“getElementsAssociatedToMaterials” returns a Group containing the list of elements associated to the material(s) given as argument(s). The argument is an integer or an Array of integers corresponding to the material IDs of the elements inserted in the list. Each integer argument can be replaced by a String corresponding to the name of the material defined in the DataBase.
“getElementsAssociatedToPlies” returns a Group containing the list of elements associated to the ply (plies) given as argument(s). The argument is an integer or an Array of integers corresponding to the property IDs of the elements inserted in the list. The ply Ids are either the ply identifiers defined with the “.PLI” command (Samcef model),.
“getNodesAssociatedToElements”. (See description in “NastranDb” class.)
“getNodesAssociatedToRbes”. (See description in “NastranDb” class.)
“getRbesAssociatedToNodes”. (See description in “NastranDb” class.)
“getElementsAssociatedToLaminates” returns a Group containing the list of elements associated to the laminate(s) given as argument(s). The argument is an integer or an Array of integers corresponding to the property IDs of the elements inserted in the list.
“getElementsAssociatedToAttr1s” returns a Group containing the list of elements of which the first attribute is included in the arguments. The argument is an integer or an Array of integers corresponding to the first attributes of the elements inserted in the list.
“getElementsAssociatedToAttr2s” returns a Group containing the list of elements of which the second attribute is included in the arguments. The argument is an integer or an Array of integers corresponding to the second attributes of the elements inserted in the list.
WARNING: due to compiler limitations, the reading of large FAC files (size>2Gb) with FeResPost 32bits library is likely to end up with an exception. If this happens, user should switch to a 64bits version of the library.
“readDesFac” method is used to import Samcef Results. The files that are read are the “des” and the “fac” files. The method may have 2, 3, 4, 5, 6 or 7 arguments:
The first argument is a String containing the name of the “des” file. This argument is mandatory.
The second argument is a String containing the name of the “fac” file. This argument is also mandatory. Of course the two “des” and “fac” files must correspond.
The third argument is optional. It is an Array of integers corresponding to the identifiers of the Load Cases for which Results are to be imported. If the argument is omitted, the Results for all load cases are imported.
The fourth argument is optional and may be present only if the third argument is defined. It corresponds to the names that will be attributed to the load case attribute of Results imported. These names are provided in an Array of Strings. If this argument is not used, the default load case names will be attributed to the Results created in the SamcefDb.
For example, without the fourth argument, the importation of asef Results with several load cases leads to LoadCase attributes named “LoadCase 1”, “LoadCase 2”,... This may be unpractical for many problems.
The fifth argument is optional and corresponds to the names of the sub-cases for which values shall be imported. These names are provided in a String or an Array of Strings. If the Array is void or the parameter is omitted, all the sub-cases are read.
The sixth argument is optional and corresponds to the names of the Results for which values shall be imported. These names are provided in a String or an Array of Strings. Possible values are "Stress Tensor", "Strain Tensor",... If the Array is void, all Result types are considered. If the Array is void or the parameter is omitted, all the Results are read.
The seventh argument is an Array of integers corresponding to the Samcef Result Codes to be considered when Results are imported.
Note that when the third and fourth arguments are used, the number of elements of the two Arrays must be the same. For more information about arguments 4, 5 and 6, see the description of “readOp2” method in “NastranDb” class.
Note that the reading of “fac” files also checks the endianness of the file and, if needed, does corrections to the binary data.
At the end of reading the method “readDesFac” prints a list of the Samcef Result Codes that have been skipped.
Presently, the method allows the reading of Results for the following Samcef modules:
Asef. The first integer ID associated to the created Results is the number of the load case. The first Real ID associated to the create Results is the deformation energy. The default case ID of the created Result objects is “Load Case x” where “x” is replaced by the integer ID of the case. The subcase ID associated to the load case is always “Statics”.
Mecano. The first integer ID associated to the created Results is the time step ID. The first Real ID associated to the create Results is the time (continuation parameter would be a more appropriate name). The default case ID of the created Result objects is “Non-Linear Load Case”. The subcase ID associated to the load case is always “Step x” where “x” is replaced by the time step index.
Dynam. The first integer ID associated to the created Results is the mode index. The first Real ID associated to the create Results is the frequency. The default case ID of the created Result objects is “Dynam Load Case”. The subcase ID associated to the load case is always “Mode x” where “x” is replaced by the mode index.
Stabi. The first integer ID associated to the created Results is the mode index. The first Real ID associated to the create Results is the critical load. The default case ID of the created Result objects is “Stabi Load Case”. The subcase ID associated to the load case is always “Mode x” where “x” is replaced by the mode index.
“readDesFac2H” method is used to read Samcef Results from “des” and the “fac” files. The method does not read the Results into the dataBase, but returns them into a Hash. For example:
...
h=db.readDesFac("~/FERESPOST/TEST_SAMCEF/mySatellite_as.des",\
"~/FERESPOST/TEST_SAMCEF/mySatellite_as.fac",\
[1],["accel_XYZ"])
...
Flags influencing the behavior of “readDesFac” method can be defined. The following singleton methods have been defined to manipulate the flags:
“desFacResetFlags” resets all the flags to false (default values). This method has no arguments.
“desFacSetFlag” sets one flag to true. This method has one String argument. An example of use of this method follows:
...
DataBase.desFacSetFlag("ANGULAR_STRAIN_BUG")
db.readDesFac("~/FERESPOST/TEST_SAMCEF/mySatellite_as.des",\
"~/FERESPOST/TEST_SAMCEF/mySatellite_as.fac",\
[1],["accel_XYZ"])
...
“desFacUnsetFlag” sets one flag to false. This method has one String argument.
“desFacGetFlag” returns a Logical value corresponding to the value of the flag. This method has one String argument.
When one of these methods has one String argument, this argument is the name of the considered flag. Among the above methods, only the last one returns a value.
Two such flags have been defined:
The flag “ANGULAR_STRAIN_BUG” is used to correct a Samcef bug when importing “Strain Tensor” Results . (See section III.2.2 for more information on the effect of this flag.)
The flag “DES_FAC_DEBUG” force SamcefDb methods related to the access to samcef Des/Fac files to issue debugging messages that might help to identify problems when trouble strike.
Similarly, two singleton methods allow to enable or disable Samcef Result codes:
“enableSamcefResCodes” is used to enable or re-enable “result codes” when reading Results from a pair of “des” and “fac” files.
“disableSamcefResCodes” is used to disable “result codes” when reading Results from a pair of “des” and “fac” files.
The argument of these two methods are an integer or an Array of integer corresponding to Samcef Result Codes.
Four methods devoted to the enabling or disabling of composite layered Results are defined in the generic “DataBase” class. These methods are presented in section I.1.3.2.
Since version 3.5.0, FeResPost allows a random access to DES/FAC result files. This method is more efficient than the methods that import Results into the DataBase, and extracting copies of these Results. A peculiar case in which the random access methods will be more efficient is when only some small parts of the Result file are of interest to the programmer.
The principle of random access is as follows:
The DES/FAC file is attached to the DataBase.
Its content (lists of load cases, sub-cases, Results...) is identified.
The Results that are needed are then read from the file.
The different methods called to perform these operations are described in the following sub-sections.
Note that the content of DES file is read only when the DES/FAC files are attached to the DataBase. After that, the DES file is closed. This is why when information is extracted from a peculiar attachment, the attachment is identified by the name of the FAC file.
The method “attachDesFac” is used to attach a DES/FAC file to the Samcef DataBase. This method has between two and four arguments:
A String containing the name of the DES file. (Full path name must be provided.)
A String containing the name of the FAC file. (Full path name must be provided.)
An integer or an Array of integers identifying load cases.
A String or an Array of Strings corresponding to the names that are attributed to the load cases and which shall be used to retrieve corresponding Results.
The arguments 3 and 4 are optional. They correspond to arguments 3 and 4 of the “readDesFac” method discussed in section III.2.1.4.
Several other methods are used to manage the DES/FAC attachments to a DataBase:
“detachDesFac” is used to delete an attachment. The method has one String argument corresponding to the name of the FAC file.
“removeAllAttachments” removes all the attachments to a DataBase. This method has no argument.
“getNbrAttachments” has no argument and returns the number of DES/FAC files attached to the DataBase.
“getAttachmentNames” has no argument and returns an Array of Strings containing the list of FAC files attached to the DataBase.
“checkAttachmentExists” has one String argument containing the FAC file name, and returns “True” if the FAC file is Attached to the DataBase, and “False” otherwise.
The following methods extract information related to the Results stored in DES/FAC files attached to the DataBase:
“getAttachmentLcInfos” returns information on load cases and sub-cases of Results found in the DataBase. The information is returned in an Array. (Format of returned Array is described in chapter III.1.)
“getAttachmentNbrLoadCases” returns the number of load cases found in an attachment.
“getAttachmentLcNames” returns an Array of Strings corresponding to the load case names found in an attachment.
“getAttachmentLcScNames” returns an Array containing two elements. The first element is an Array of String containing the load case names found in the FAC file. The second element is an Array of String containing the sub-case names found in the FAC file.
“getAttachmentLcScResNames” returns an Array of three elements. Each element is an Array of Strings. The first element is the list of load case names. The second element is the list of sub-case names. The last element is the list of Result names.
“getAttachmentNbrLayers” returns the number of layers identified in an attachment.
“getAttachmentLayerIds” returns an Array of Integers corresponding to the identifiers of the layers found in an attachment.
“getAttachmentLayerNames” returns an Array of Strings corresponding to the names of the layers found in an attachment.
“getAttachmentNbrSubLayers” returns the number of sub-layers identified in an attachment.
“getAttachmentSubLayerIds” returns an Array of Integers corresponding to the identifiers of the sub-layers found in an attachment.
“getAttachmentSubLayerNames” returns an Array of Strings corresponding to the names of the sub-layers found in an attachment.
All these methods have a single String argument containing the name of the FAC file that must have been previously attached to the DataBase. On the other hand, the following methods have one or two arguments:
“getAttachmentNbrSubCases” returns the number of sub-cases found in an attachment.
“getAttachmentScNames” returns an Array of Strings corresponding to the sub-case names found in an attachment.
“getAttachmentNbrResults” returns the number of Result names identified in an attachment.
“getAttachmentResIds” returns an Array of Integers corresponding to the identifiers of the Results found in an attachment.
“getAttachmentResNames” returns an Array of Strings corresponding to the names of the Results found in an attachment.
The first argument is the name of the FAC file that must have been previously attached to the DataBase. The second argument is optional and corresponds to the name of a load case found in the attached FAC file. If the argument is not provided, all the load cases are investigated to build the list of sub-cases or Result names or IDs. If the argument is provided, only the sub-cases or Results of the corresponding load case are considered. If the provided load case does not exist in FAC attachment an error message is issued.
The method “getAttachmentResults” is used to read Results from the FAC file. The Results are directly returned by the method to the caller. They are not inserted in the DataBase from which the method is called.
The method has minimum four arguments:
A String corresponding to the name of FAC file attachment from which Results are read. (This file must have been previously attached to the DataBase.)
A String corresponding to the name of the load case for which Results are read.
A String or an Array of Strings corresponding to the names of sub-cases for which Results are read.
A String or an Array of Strings corresponding to the names of Results for which Results are read.
The other arguments are optional and correspond to the specification of target entities for which Results are read. Actually, the reading operation from a FAC file combines the reading and some of the extraction operations described in section I.4.3. For example:
The fifth argument can be a ResKeyList object. Then the Results are extracted on the keys of the ResKeyList object.
The fifth argument can be a Result object. Then the Results are extracted on the keys of the Result object.
Extractions can be performed on Groups. Then one specifies the target by a “Method” String argument and a “GrpTarget” Group argument. The possible values of the “Method” argument are listed in section I.4.3.1. (Description of “extractResultOnEntities” method in the Result class.) When Results are extracted on Groups, one can also specify list of layers and sub-layers for which values are extracted. This argument is optional. (See below.)
One can also specify a list of layers by providing a parameter which is an Array of String or Integer values. Note however that the filtering on layers is done only when Results for which several layers can be read. For example, this parameter does not influence the reading of MPC Forces, Shell Forces...
One can also specify a list of sub-layers by providing a parameter which is an Array of String or Integer values. Note that this last parameter influences only the reading of laminate stresses or strains. The reading of solid or shell element stresses and strains is not affected by this parameter.
One can extract Results without specifying the ResKeyList, Result or Group argument. However, it is still possible to specify a list of layers, a list of sub-layers, and a location to filter the values that are inserted in Results. The “Location” argument corresponds to the “Method” argument when Results are extracted on Groups. Possible values of this parameter are “Elements”, “ElemCenters", “ElemCorners”...
Only lists below the list of valid calls to “getAttachmentResults”:
h=db.getAttachmentResults(facName,lcName,scNames,resNames, method,grpTarget[,layers[,subLayers]]) h=db.getAttachmentResults(facName,lcName,scNames,resNames, resTarget) h=db.getAttachmentResults(facName,lcName,scNames,resNames, rklTarget) h=db.getAttachmentResults(facName,lcName,scNames,resNames [,layers[,sub-Layers[,location]]])
As several Result types, and sub-case names can be given as argument to “getAttachmentResults” method, this method can return several Results. This is why Results are returned in a Hash:
The Hash keys are Array of three Strings corresponding to the name of the load case, the name of the sub-case, and the Result type name respectively.
The Hash values are the Results.
For example, the list of extracted Result sizes can be printed with the following statements:
h=db.getAttachmentResults(facName,lcName,scNames,resNames,"Nodes",grp)
h.each do |id,res|
lcName=id[0]
scName=id[1]
resName=id[2]
size=res.Size
STDOUT.printf("%s - %s - %s : %d\n",lcName,scName,resName,size)
#~ Util::printRes(STDOUT,"brol",res)
end
The method “getAttachmentResultsCombili” is used to extract linear combinations of elementary Results found in one or several attached FAC files. As for method “getAttachmentResults” the Results are directly returned by the method to the caller. They are not inserted in the DataBase from which the method is called. This method is more or less a combination of the methods “getAttachmentResults” and “buildLoadCasesCombili” of the generic DataBase class.
Practically, the main difference between “getAttachmentResults” and “getAttachmentResultsCombili” is that the first argument is no longer a FAC file name. This argument is removed. Instead, one provides a “Combili” argument that describes the linear combination corresponding to extracted Results. This “Combili” argument is the second argument. The first argument is the “LcName” argument corresponding to the load case name attributed to the generated Results. This load case name is not supposed to correspond to any load case name found in the attached FAC file(s).
The method has minimum four arguments:
A String corresponding to the name of the load case for which Results are read.
A “Combili” Array containing the description of the linear combination of elementary load case Results. The Array is an Array of Arrays. Each secondary Array contains three elements:
A Real value corresponding to the factor in the linear combination.
A String corresponding to the name of the FAC file from which elementary Results are read. This file must have been previously attached to the Samcef DataBase.
A String corresponding to the name of the load case for which Results are extracted.
A String or an Array of Strings corresponding to the names of sub-cases for which Results are read.
A String or an Array of Strings corresponding to the names of Results for which Results are read.
The other arguments are optional and correspond to the specification of target entities for which Results are read. Actually, the reading operation from a FAC file combines the reading and some of the extraction operations described in section I.4.3. For example:
The fifth argument can be a ResKeyList object. Then the Results are extracted on the keys of the ResKeyList object.
The fifth argument can be a Result object. Then the Results are extracted on the keys of the Result object.
Extractions can be performed on Groups. Then one specifies the target by a “Method” String argument and a “GrpTarget” Group argument. The possible values of the “Method” argument are listed in section I.4.3.1. (Description of “extractResultOnEntities” method in the Result class.)
One can also specify a list of layers by providing a parameter which is an Array of String or Integer values.
One can also specify a list of sub-layers by providing a parameter which is an Array of String or Integer values.
One can extract Results without specifying the ResKeyList, Result or Group argument. However, it is still possible to specify a list of layers, a list of sub-layers, and a location to filter the values that are inserted in Results. The “Location” argument corresponds to the “Method” argument when Results are extracted on Groups. Possible values of this parameter are “Elements”, “ElemCenters", “ElemCorners”...
Only lists below the list of valid calls to “getAttachmentResultsCombili”:
h=db.getAttachmentResultsCombili(lcName,combili,scNames,resNames, method,grpTarget,layers) h=db.getAttachmentResultsCombili(lcName,combili,scNames,resNames, method,grpTarget) h=db.getAttachmentResultsCombili(lcName,combili,scNames,resNames, resTarget) h=db.getAttachmentResultsCombili(lcName,combili,scNames,resNames, rklTarget) h=db.getAttachmentResultsCombili(lcName,combili,scNames,resNames, layers) h=db.getAttachmentResultsCombili(lcName,combili,scNames,resNames)
The Hash object returned by the method has a structure identical to the one returned by “getAttachmentResults” and can be manipulated the same way.
In order to reduce the number of accesses to disk, it may be useful to store some of the blocks read from binary result files into memory. FeResPost provides an algorithm that allows to store the blocks most recently read for later usage. Two singleton methods of the “SamcefDb” class allow the to tune the capacity of the buffer area:
“setStorageBufferMaxCapacity” sets the capacity of storage. The method has one arguments: a real value containing the size in Megabytes of the buffer.
“getStorageBufferMaxCapacity” returns the storage buffer current total capacity. The returned value is a real that corresponds to the capacity in Megabytes of the buffer. The method has no argument.
Note that all buffers are now common to all the methods that provide random access to XDB and FAC result files. In particular, the method is used in management of the binary file access for XDB and FAC attachment or reading. This means that if one Result file attached to one DataBase is more used, the storage will contain a majority of buffers for this Result file and progressively delete the other buffers.
The default capacity for storage buffer is 0Mb. Note that the two methods described above can be called from any class derived from the generic “DataBase” class.
The method “writeGmshMesh” defined in DataBase Class exports nodes and elements into the mesh file. The three tags attributed to the elements are the first and second element attributes and the laminate ID.
The method “generateShellOffsetsResult” defined in SamcefDb Class generates a Result corresponding to shell offsets for 2D elements. The method has no argument or three arguments. The arguments correspond to the key to which the Result object is associated in the SamcefDb object. (load case name, subcase name, and result name respectively.) If the String arguments are omitted, one assumes “”, “” and “Coordinates” for the Result key.
A first group of iterators iterate on finite element entities of the finite element model stored in the DataBase.
“each_coordSysId” iterates on the integer identifiers of coordinate systems.
“each_elemId” iterates on the integer identifiers of elements.
“each_materialId” iterates on the integer identifiers of materials.
“each_samcefPlyId” iterates on the integer identifiers of samcef plies.
“each_samcefLaminateId” iterates on the integer identifiers of samcef laminates.
The elements produced by the iterator are single integers. Each of these iterators has 0, 1 or 2 arguments. The two optional arguments are the integer bounds considered for the iteration: “IdMin” and “IdMax”.
Two methods allow the iteration on the elements of associative containers used to record the correspondence between integer and String identifiers of the samcef Groups stored in the DataBase:
“each_samcefMatIdName” produces pairs of integer and String elements.
“each_samcefMatNameId” produces pairs of String and integer elements.
Two iterators loop on the nodes defining an element:
These two iterators have one integer argument corresponding to the index of the element. The return the integer indices of nodes.
Several other methods allow to obtain model information.
“getNodeRcId” has an integer argument corresponding to the node ID and returns the corresponding reference coordinate system ID.
“getNodeAcId” has an integer argument corresponding to the node ID and returns the corresponding analysis coordinate system ID.
“getNodeCoords” returns the coordinates of a node. This method has one or two arguments:
The first argument is an integer corresponding to the node ID.
The second argument is an integer or a string that corresponds to the coordinate system in which the coordinates are expressed. The argument is an integer, or the “AsIs” string. Note that if the argument is missing, the “AsIs” coordinate system is considered.
One attribute “getter” allows to access information in the model:
“NbrRbes” returns the number of rigid body elements stored in finite element model. This method has no argument.
One makes here the distinction between general Results and composite Results.
General Results (by opposition to Composite Results) are presented in Tables III.2.2 to III.2.4. (One makes the distinction between Scalar, Vectorial and Tensorial Results.) About the Results described, one can make the following comments:
The shear components of strain tensor output by Samcef should be (and generally are) components of a tensor (). The same convention is used for all the tensors manipulated in FeResPost. So, no manipulation of the shear components is made when importing strain tensors from Samcef Results.
Note however that because of a bug in Samcef, strain results given at center of elements may be wrong and use the “angular deformation” convention. So the use should be careful when manipulating strain tensor Results imported from Samcef.
A flag influencing the importation of Results with “readDesFac” method allows the modification of shear components of 2D elements strain tensor: the ‘ANGULAR_STRAIN_BUG” flag. When set to “true”, the shear components of Strain tensor are divided by two. This division by two is done for the result codes 3421, 3445 and 3446. It is the responsibility of the user to check whether the setting of the flag is necessary or not.
See more information about the methods used to manipulate the flags in section III.2.1.4.
The ”Mechanical Strain Tensor” Result corresponds to the Strain Tensor estimated from Stress Tensor without considering thermo-elastic or hygro-elastic effects into account.
All result codes corresponding to Von Mises stress are skipped. However, Von Mises stress can always be generated by derivation from stress tensor Results.
The Result “Shell Forces” contains the contributions of several Samcef Result codes: the shell element normal forces (code x437) and the shell element shear forces (code x251).
Samcef “beam” type elements do not output vectorial or tensorial forces or moments. Instead, the different components are expressed in different coordinate systems. When importing these Results, a conversion into tensorial format is done as follows:
|
|
|
|
(One uses here the notation of the Samcef manual for the components stored in “fac” file: corresponds to the axial component of force, to the shear forces, to the torsion moment and to the bending moment.)
Beam forces and moments are also saved in “fac” file for bushing elements. Then, the longitudinal axis may be if axisymmetric properties are attributed to the element. Then, the components are inserted in 2D tensors as follows:
|
|
|
|
| Samcef Result Code | Generated Result |
| 334 | “Element Strain Energy (Density)” |
| 335 | “Element Kinetic Energy (Density)” |
| 3234 | “Element Strain Energy (Percent of Total)” |
| 3235 | “Element Kinetic Energy (Percent of Total)” |
| 1305 | “Contact, Contact Pressure” |
| 1306 | “Contact, Friction Stress” |
| 1307 | “Contact, Normal Distance” |
| 2051 | “Contact, Nodal Distance” |
| 1440, 3440 | “Beam Axial Stress for Total Loads” |
| 1450, 3450 | “Beam Shear Stress for Total Loads” |
| Samcef Result Code | Generated Result |
| 153 | “Coordinates” |
| 163 | “Displacements, Translational” |
| 191 | “Displacements, Rotational” |
| 221 | “Reaction Forces, Forces”, “Reaction Forces, Moments” |
| 1439, 3439, 1524, 3524 | “Beam Forces” (5) |
| 1439, 3439, 1525, 3525 | “Beam Moments” (5) |
| 1532 | “Grid Point Forces, Reaction Forces” |
| 1533 | “Grid Point Forces, Reaction Moments” |
| 1534 | “Grid Point Forces, Internal Forces” |
| 1535 | “Grid Point Forces, Internal Moments” |
| Samcef Result Code | Generated Result |
| 120 | “Temperature” |
| 121 | “Temperature Variation Rate” |
| 1379, 3379 | “Specific Heat Energy” |
| 1511, 3511 | “Conductive Heat Flux” |
| 1801, 3801 | “Applied Heat Flux” |
One presents below a few comments above the composite Results presented in Tables III.2.6 to III.2.8:
Composite Results have non-linear dependence on the primary unknowns (displacements and rotations). Therefore, composite Results obtained by linear combination of elementary Results are false.
With Samcef, it is also possible to output ply Results in the upper and lower layers of each ply (codes 1xxxx and 2xxxx). FeResPost reads results at mid layer of each ply only. The other Results are skipped. (Note that most composite calculation methods usually use the forces in plies recovered at mid-thickness.)
Even though the maximum stress and strain failure indices are presented in Samcef and FeResPost as tensorial Results, the six components for each location are not the components of a tensor. Therefore, the user must be very careful when using those Results. In particular transformations of coordinate systems for those Results are meaningless.
Composite critical ply failure indices give for each element the maximum failure index in one of the plies. Also, the evaluation is done at the Gauss points of each ply and each elements and the maximum is collected.
Four methods devoted to the enabling or disabling of composite layered Results are defined in the generic “DataBase” class. These methods are presented in section I.1.3.2.
| Samcef Result Code | Generated Result |
| *1621, *3621 | “Composite Failure Index, Tsai-Hill Version 1” |
| *1622, *3622 | “Composite Failure Index, Tsai-Hill Version 2” |
| *1623, *3623 | “Composite Failure Index, Tsai-Hill Version 3” |
| *1624, *3624 | “Composite Failure Index, Tsai-Wu” |
| *1625, *3625 | “Composite Failure Index, Hashin Version 1” |
| *1626, *3626 | “Composite Failure Index, Hashin Version 2” |
| *1627, *3627 | “Composite Failure Index, Hashin Version 3” |
| *1630, *3630 | “Composite Failure Index, Stress Ratio” |
| *1631, *3631 | “Composite Failure Index, Strain Ratio” |
| *1632, *3632 | “Composite Failure Index, Rice and Tracey” |
| *7621 | “Composite Critical Ply Failure Index, Tsai-Hill Version 1” |
| *7622 | “Composite Critical Ply Failure Index, Tsai-Hill Version 2” |
| *7623 | “Composite Critical Ply Failure Index, Tsai-Hill Version 3” |
| *7624 | “Composite Critical Ply Failure Index, Tsai-Wu” |
| *7625 | “Composite Critical Ply Failure Index, Hashin Version 1” |
| *7626 | “Composite Critical Ply Failure Index, Hashin Version 2” |
| *7627 | “Composite Critical Ply Failure Index, Hashin Version 3” |
| *7628 | “Composite Critical Ply Failure Index, Maximum Strain, CompMax” |
| *7629 | “Composite Critical Ply Failure Index, Maximum Stress, CompMax” |
| *7630 | “Composite Critical Ply Failure Index, Stress Ratio” |
| *7631 | “Composite Critical Ply Failure Index, Strain Ratio” |
| *7632 | “Composite Critical Ply Failure Index, Rice and Tracey” |
| Samcef Result Code | Generated Result |
| 8621 | “Composite Critical Ply, Tsai-Hill Version 1” |
| 8622 | “Composite Critical Ply, Tsai-Hill Version 2” |
| 8623 | “Composite Critical Ply, Tsai-Hill Version 3” |
| 8624 | “Composite Critical Ply, Tsai-Wu” |
| 8625 | “Composite Critical Ply, Hashin Version 1” |
| 8626 | “Composite Critical Ply, Hashin Version 2” |
| 8627 | “Composite Critical Ply, Hashin Version 3” |
| 8628 | “Composite Critical Ply, Maximum Strain, CompMax” |
| 8629 | “Composite Critical Ply, Maximum Stress, CompMax” |
| 8630 | “Composite Critical Ply, Stress Ratio” |
| 8631 | “Composite Critical Ply, Strain Ratio” |
| 8632 | “Composite Critical Ply, Rice and Tracey” |
| Samcef Result Code | Generated Result |
| 1628, 3628 | “Composite Failure Index, Maximum Strain” |
| 1629, 3629 | “Composite Failure Index, Maximum Stress” |
The correspondence between the failure indices read from Samcef result files and Results produced by CLA classes is as in Table III.2.9. Sometimes a single Samcef Result corresponds to two different CLA failure criteria. Then, the type of element (2D or 3D) allows the identification of the appropriate CLA criterion.
| Samcef Result | CLA criterion ID | section |
| “Composite Failure Index, Tsai-Hill Version 1” (2D elements) | “TsaiHill_b” | II.1.10.10 |
| “Composite Failure Index, Tsai-Hill Version 1” (3D elements) | “TsaiHill3D_b” | II.1.10.13 |
| “Composite Failure Index, Tsai-Hill Version 2” (2D elements) | “TsaiHill” | II.1.10.9 |
| “Composite Failure Index, Tsai-Hill Version 2” (3D elements) | “TsaiHill3D” | II.1.10.12 |
| “Composite Failure Index, Tsai-Hill Version 3” | “TsaiHill” | II.1.10.9 |
| “Composite Failure Index, Tsai-Wu” | “TsaiWu3D” | II.1.10.15 |
| “Composite Failure Index, Hashin Version 1” | “Hashin3D” | II.1.10.21 |
| “Composite Failure Index, Hashin Version 2” | “Hashin3D_b” | II.1.10.21 |
| “Composite Failure Index, Hashin Version 3” | “Hashin3D_c” | II.1.10.21 |
| “Composite Failure Index, Hoffman” | “Hoffman” | II.1.10.16 |
| “Composite Failure Index, Maximum Strain, CompMax” | “MaxStrain3D” | II.1.10.7 |
| “Composite Failure Index, Maximum Stress, CompMax” | “MaxStress3D” | II.1.10.5 |
| “Composite Failure Index, Interlaminar Shear Stress” | “Ilss” | II.1.10.27 |
Important remarks must be done about the coordinate system associated to each value in the Result objects:
The “ElemCS” coordinate system is obtained from the element topology. This means that it can be reconstructed using the nodes defining the element. So the element coordinate system looks more like a Nastran element coordinate system. This remark is necessary because Samcef documentation uses often the words “element coordinate system” to qualify what is rather a material coordinate system.
The “ElemIJK” coordinate system is the same as “ElemCS”.
The “MatCS” coordinate system corresponds to what is often called “element coordinate system” in Samcef documentation. This modification of terminology has been done to have a meaning closer to the one of Nastran Results.
The method “readGroupsFromSamcefDat” reads Groups from a Samcef Bacon data file and returns a Hash containing the list of Groups. (This method is similar to “readGroupsFromPatranSession” also defined in “Post” module.) The keys are Group names, and the values are the Groups. The method has two arguments:
A String corresponding to the name of the session file.
A DataBase. This argument is optional. If it is provided, the reading method removes from the created Groups all the entities undefined in the DataBase argument.
The definition of Groups must be done according to the “.SEL” command of the Bacon files. Only the lines in the “.SEL” commands are considered. More model definition command may be present in the file but they are ignored. Examples of use of the method follow:
...
h=Post::readGroupsFromSamcefDat("groups.dat")
...
h=Post::readGroupsFromSamcefDat("groups.dat",DB)
...
This Part of the document is devoted to the presentation of examples illustrating various aspects of FeResPost All the FeResPost example are done with a model and Nastran results corresponding to a very simplified and imaginary satellite represented in Figure IV.1.1. This Part is organized as follows:
The finite element model of the structure is described in Chapter IV.1. In that Chapter, one also gives information that will help the reader to use the finite element in the various examples.
In Chapter IV.2, one presents small examples of ruby programs using the FeResPost library and finite element model and results of the “testSat” satellite. These results illustrate the use of various classes and methods of the FeResPost library.
In Chapter IV.4, one presents an example of object-oriented post-processing program written with ruby and using FeResPost library. The program uses the model and results of “testSat” satellite to calculate margins of safety in honeycomb, skins and connections. This project results from an evolution of a former project. (Previous versions of this project are described and discussed in Appendixes IV.4 and X.E.4.)
Chapter IV.3 presents a few examples that illustrate the use of composite classes.
All the examples are delivered in “TESTSAT” directory. This directory contains four subdirectories:
“MODEL” contains the definition “testSat” finite element model. The splitting of this model into several files and its organization in sub-directories is described in section IV.1.6.
“OTHER_EXECS” contains Nastran example BDF files not related to the “testSat” small satellite finite element model. In general, these examples illustrate technicalities of Nastran and FeResPost.
“RUBY” contains the small examples described in Chapter IV.2. The sub-directories in “RUBY” are:
The different “EX??” directories containing the small examples.
“PROJECT” is the main directory of the modular program described in chapter IV.4. Each
“PROJECTa” is the main directory of the modular program described in Appendix X.D.2. Each
“PROJECTb” is the main directory of the object oriented program described in Appendix X.E.4.
Finally, a “EXEC_OP2” directory has been defined in “MODEL” directory. The main bulk data files have been copied in this directory and the calculations with Nastran must be performed in that directory.
Similarly a “EXEC_XDB” directory has been defined in “MODEL” directory. There, the main bulk data files have been modified to produce “xdb” result outputs.
Of course, before running the examples, you must compile ruby or its shared library, and produce the Nastran finite elements results.
Typically, one imports the FeResPost Classes and Modules with the two following statements:
require "FeResPost" include FeResPost
Note however that it works only if the different environment variables have been initialized correctly. Typically, in our Windows examples, this is done through the batch files (on Windows computers) or bash files (on UNIX and LINUX computers) that are used to launch the example scripts, and the following variables are generally initialized:
set LIB= set INCLUDE= set RUBYPATH=C:/NEWPROGS/RUBY/ruby-3.0.0-1-x64/bin set REDISTRPATH=C:/Users/ferespost/Documents/SRC/OUTPUTS/REDISTR set RUBYLIB=C:/Users/ferespost/Documents/SRC/OUTPUTS/RUBY/RUBY_30 set PATH=%RUBYPATH%;%REDISTRPATH%;C:/Windows/System32
On Windows machines, the examples are defined in such a way that the environment is defined in file “RUBY/ENV/env.bat” included in the script used to launch ruby program. In the example above, not that the “PATH” environment variable refers to tree directories:
The directory containing ruby executable.
The directory containing redistributable shared libraries from the compiler used to compile FeResPost.
The directory containing Windows 32 bits system libraies. (This directory is “C:/Windows/SysWow64” for 64 bits versions of ruby and FeResPost.)
For example, the example “EX03/makeGravForces.rb” is launched in “RUBY/EX06” directory with command:
makeGravForces.bat
in which “exec” refers to the “exec.bat” file with following content:
setlocal call "../ENV/env.bat" ruby -I. makeGravForces.rb endlocal
Of course the different paths you will initialize in “ENV/env.bat” will have to be adapted to you peculiar installation, and to the version of Ruby you are using.
On unix, the BASH file looks as follows:
#!/bin/bash source ../ENV/env.bash ruby --version ruby -I. -I$RUBYLIB makeGravForces.rb
in which“../ENV/env.bash” content looks like:
RUBYLIB=/home/progs/Documents/FERESPOST/SRC/OUTPUTS/RUBY/RUBY_25 PATH=/home/PGR/RUBY/I64//RUBY_251/bin
In this Chapter, one describes the finite element model used in all the examples. The Chapter is organized as follows:
In section IV.1.1, one presents the satellite’s structure and its finite element model.
The materials and element properties are described in section IV.1.2.
The conventions used for the numbering of nodes, elements and RBEs, and the groups that have been defined are given in section IV.1.3.
In section IV.1.4, the loads and boundary conditions used in the examples of Chapter IV.2 are presented.
Finally, one briefly describes in section IV.1.6 the way the FE model has been split into several bulk data files, and the organization of these files into several directories.
An overall view of the satellite’s FE model is presented in Figure IV.1.1. Basically, the structure is composed of an hexahedral lower box and of an upper panel supported by six struts. The hexahedral lower box is made of six sandwich panels connected on 12 metallic bars along their edges. The metallic bars are connected to eight corner nodes. A view of the lower box metallic frame, without the sandwich panels is given in Figure IV.1.2. The corner nodes, and the connections of sandwich panels are modeled with RBE2 elements. However, for thermo-elastic calculations these RBE2 elements are replaced by very stiff CBAR elements.
The sandwich panels are generally modeled with volumic elements for the honeycomb and surfacic elements for the skins (Figure IV.1.3). A surfacic modeling of a sandwich panel with layered (PCOMPG) element properties has been chosen for only one of the panels: the bottom panel.
To ensure a good transfer of loads to the panels, in particular of the bending moments at connections, small traversing elements have been introduced in the panels modeled with 3D elements. Those elements represent the inserts and connect the two skins. A global view of all the traversing elements is given in Figure IV.1.4.
The struts are modeled with CBAR elements. The struts are connected to the upper panel and to the box +Z panel through metallic fittings modeled with CONM2 and RBE2 elements. (The RBE2 elements are replaced by very stiff CBAR elements for thermo-elastic calculations). The connections of struts to the fittings are ball-bearing connections (only translational degrees of freedom are transmitted, except on the lower side, where the rotation of each strut around its axis is blocked).
The equipments connected to the sandwich panels are modeled with CONM2 and RBE2 elements. (The RBE2 elements are replaced by very stiff CBAR elements for thermo-elastic calculations). A view of some equipments is presented in Figure IV.1.5. On some panels small equipments are modeled by adding a NSM (non-structural mass) to PSHELL properties.
In the satellite FE model, only seven material cards are defined. The most relevant parameters of material cards are given in Tables IV.1.1, IV.1.2 and IV.1.3.
| Material name | MID | (GPa) | () | () | |
| Al-7075-T7351 | 2 | 72.1 | 0.33 | 2796.0 | |
| Al-7010-T7451 | 1 | 71.7 | 0.33 | 2820.0 | |
| Al-2024-T3 clad | 3 | 69.0 | 0.33 | 2768.0 | |
| (thermo-elastic) | 5001 | 72.1 | 0.33 | 0.0 | |
| Material type | Honeycomb 50 | Honeycomb 72 |
| MID | 5 | 6 |
| (MPa) | 0.670 | 0.760 |
| (MPa) | 0.670 | 0.760 |
| (MPa) | 669.0 | 1276.0 |
| (MPa) | 0.207 | 0.310 |
| (MPa) | 138.0 | 193.0 |
| (MPa) | 310.0 | 483.0 |
| () | 50 | 72 |
| () | ||
| Material type | Honeycomb 50 2D | CFRP 2D |
| MID | 4 | 10000 |
| (MPa) | 0.500 | 290000 |
| (MPa) | 0.500 | 5600 |
| 0.3 | 0.33 | |
| (MPa) | 0.500 | 3000 |
| (MPa) | 310.0 | 1100 |
| (MPa) | 138.0 | 1100 |
| () | 50 | 1670 |
| () | ||
| () | ||
| (MPa) | 0.050 | 1600 |
| (MPa) | 0.050 | 500 |
| (MPa) | 0.050 | 25 |
| (MPa) | 0.050 | 140 |
| (MPa) | 0.050 | 55 |
All CBAR elements receive PBARL properties:
For the traversing elements representing the inserts in sandwich panels, one assumes a cylinder of 16 mm diameter. The material is Al 7010 T7451.
The bars of metallic frame receive Al 7010 T7351 material and have a tubular cross-section with 26 mm and 30 mm internal and external diameters respectively.
The bars of struts receive Al 7010 T7351 material and have a tubular cross-section with 46 mm and 50 mm internal and external diameters respectively.
Finally, when RBE2 elements are replaced by very stiff CBAR elements for thermo-elastic calculations, one attributes the fake material 5001 to the CBAR elements. This material is equivalent to Al 7010 T7351 but has no density. The bar cross-section is assumed to be a rod of 30 mm diameter.
All skins, except those of bottom panel, are made of Aluminum 2024 T3 and have a thickness of 0.5 mm. The honeycomb used in sandwich panels has a density of 50 . Only in the +Z panel of the box a 72 honeycomb has been used. The bottom panel is modeled with surface elements, and has correspondingly a PCOMPG property card (PID=6). Each skin of the bottom sandwich panel is made of CFRP laminated material with plies 0.1 mm thick. The properties are defined as follows:
PCOMPG 6 50.779 30.+6 HILL 20. 0. 2008 10000 1.-4 0. YES 2007 10000 1.-4 45. YES 2006 10000 1.-4 -45. YES 2005 10000 1.-4 90. YES 2004 10000 1.-4 90. YES 2003 10000 1.-4 -45. YES 2002 10000 1.-4 45. YES 2001 10000 1.-4 0. YES 100 4 .0284 0. YES 3001 10000 1.-4 0. YES 3002 10000 1.-4 45. YES 3003 10000 1.-4 -45. YES 3004 10000 1.-4 90. YES 3005 10000 1.-4 90. YES 3006 10000 1.-4 -45. YES 3007 10000 1.-4 45. YES 3008 10000 1.-4 0. YES
For sandwich panels modeled with solid elements, the honeycomb is oriented in such a way that the direction Z is perpendicular to the panel. Direction X is vertical for vertical panels and oriented towards +X of coordinate system 1001 for horizontal panels.
In order to ease the writing of post-processing scripts and the management of FE model, one defines numbering ranges for various parts of the model. The main numbering ranges are given in Table IV.1.4 with the associated groups, when a corresponding group exists. These groups are defined in the Patran session file “groups.ses”.
| Part | group name | numbering range |
| panel -X | “pan_MX” | 20000:24999 |
| panel -Y | “pan_MY” | 40000:44999 |
| panel -Z | “pan_MZ” | 60000:64999 |
| panel +X | “pan_PX” | 30000:34999 |
| panel +Y | “pan_PY” | 50000:54999 |
| panel +Z | “pan_PZ” | 70000:74999 |
| upper panel | “pan_SUP” | 90000:94999 |
| metallic frame | — | 80000:84999 |
| struts | “struts_ALL” | 85000:89999 |
Other groups are defined in the session file:
Groups corresponding to the various bars of the metallic frame. They are named
“bar_MXMY”, “bar_MXPY”,... There are 12 such groups that contain the CBAR tube
elements, the RBE2 connecting the sandwich panels to the metallic frame (or the
corresponding stiff CBAR elements for thermo-elastic calculations), and the nodes of the
sandwich panels connected to the bar.
Groups corresponding to the corner nodes of the metallic frame. Each groups contains one CONM2, one RBE2 (or corresponding CBAR elements), and the corresponding nodes. Those groups are named “corner_MXMYMZ”, “corner_MXMYPZ”,...
Groups corresponding to the struts’ fittings. These groups are defined with conventions similar to the groups of corner nodes. Those groups are named “fitting_MX”, “fitting_PX”,...
Six groups corresponding to individual struts. These groups are named “strut_A”, “strut_B”, “strut_C”,...
One give here information on the various loads and boundary conditions used in the examples presented in Chapter IV.2.
One makes the distinction between load cases corresponding to quasi-static accelerations or forces applied on the structure and thermo-elastic loads cases.
First, three load cases corresponding to quasi-static accelerations applied to the entire satellite structure are defined in file “unit_accel.bdf”. These accelerations are defined by Nastran “GRAV” cards and are oriented in directions X, Y and Z. Their Load identifiers are 601001, 601002 and 601003 respectively.
Then loads corresponding to quasi-static acceleration on parts of the structure are created by defining the appropriate force fields. The method used to defined those force fields is explained in the example presented in section IV.2.5.1. Six files contain these force fields:
In file “force1_PAN_PZ.bdf”, one defines a force field corresponding to a unit acceleration one the panel +Z and on the instrument. The force field corresponds to load id 616001. Similarly, one defines force fields in directions Y and Z with ids 616002 and 616003 respectively.
Similarly on defines unit acceleration fields on the upper part of the structure in files “force*_UPPER.bdf” (the upper panel, the struts and the fittings). These force fields correspond to load IDs 617001, 617002 and 617003 respectively.
One also defines temperature fields for thermo-elastic load cases calculations:
In files “temp_M100_PAN_PZ.bdf” and “temp_M100_PAN_PZ.bdf” one defines temperature fields on the +Z panel. The two files correspond to a temperature of -100 C and +120 C respectively. The corresponding load ids are 621001 and 621002.
In files “temp_M100_PAN_PANLAT.bdf” and “temp_M100_PAN_PANLAT.bdf” one defines temperature fields on lateral panels. The two files correspond to a temperature of -100 C and +120 C respectively. The corresponding load ids are 622001 and 622002.
In files “temp_GRAD_X.bdf”, ‘temp_GRAD_Y.bdf” and ‘temp_GRAD_Z.bdf”, on defines three temperature gradients of 100 C/m on the entire structure in directions X, Y and Z respectively. The corresponding load ids are 623001, 623002 and 623003.
The method used to defined these temperature fields is explained in the example presented in section IV.2.5.2.
Only two different fixations of the satellite are used in the examples of Chapter IV.2:
The fixations stored in file “launch.bdf” correspond to the clamping of the four lower corner nodes of the satellite. Practically, this is done by defining an RBE2 corresponding to the launcher interface. The six degrees of freedom of the master node are fixed by an SPC. This fixation can be selected by its number identifier: 701001.
The fixations stored in file “orbit.bdf” correspond to a fixation of the six rigid modes. This is done by defining the appropriate RBE3 element, with CELAS and SPC. This fixation is particularly adapted to the calculation of thermo-elastic load cases in orbit and is selected by its identifier 702001.
In the definition of main data files, one tried to avoid the definition of too many load cases one the structure. Therefore, one defines elementary load cases on the structure. The Results of these load cases can be recombined at post-processing level to produce the recombined Results.
The elementary load cases are defined in the following sections. One also summarizes the additional calculations that have been performed with Nastran to allow the testing of Result importation for other Nastran Solution Sequences.
One defines two data files corresponding to unit accelerations applied to the entire structure. These data files correspond to the static and thermo-elastic versions of the model respectively. On the static model, the corresponding load case names are:
“LAUNCH_ONE_MS2_X” for a unit acceleration in direction X.
“LAUNCH_ONE_MS2_Y” for a unit acceleration in direction Y.
“LAUNCH_ONE_MS2_Z” for a unit acceleration in direction Z.
These load cases are defined in file “unit_xyz.bdf”. Correspondingly, one defines unit load cases on the thermo-elastic version of the model in file “orbit_unit_xyz.bdf”:
“ORBIT_ONE_MS2_X” for a unit acceleration in direction X.
“ORBIT_ONE_MS2_Y” for a unit acceleration in direction Y.
“ORBIT_ONE_MS2_Z” for a unit acceleration in direction Z.
Two data files corresponding to the local unit acceleration fields defined in section IV.1.4.1. These files are named “unit_xyz_pan_pz.bdf” and “unit_xyz_upper.bdf” respectively. They define the following load cases:
“PANPZ_ONE_MS2_X” for a unit acceleration in direction X on panel +Z.
“PANPZ_ONE_MS2_Y” for a unit acceleration in direction Y on panel +Z.
“PANPZ_ONE_MS2_Z” for a unit acceleration in direction Z on panel +Z.
“UPPER_ONE_MS2_X” for a unit acceleration in direction X on upper part of the structure.
“UPPER_ONE_MS2_Y” for a unit acceleration in direction Y on upper part of the structure.
“UPPER_ONE_MS2_Z” for a unit acceleration in direction Z on upper part of the structure.
One defines also two data files corresponding to the definition of thermo-elastic load cases on the structure. The file “temp_disc.bdf” defines four load cases in which discontinuous temperature fields are applied to the structure. The four load cases are defined as follows:
“TEMP_PZ_COLD” corresponds to a temperature of -100 C on panel +Z and -50 C on the rest of the structure.
“TEMP_PZ_HOT” corresponds to a temperature of 120 C on panel +Z and 70 C on the rest of the structure.
“TEMP_PANLAT_COLD” corresponds to a temperature of -100 C on lateral panels and -50 C on the rest of the structure.
“TEMP_PANLAT_HOT” corresponds to a temperature of 120 C on lateral panels and 70 C on the rest of the structure.
The file “temp_grad.bdf” defines three load cases corresponding to gradients of 100 C/m applied on the entire satellite:
“TEMP_GRAD_X” corresponds to a gradient in direction X.
“TEMP_GRAD_Y” corresponds to a gradient in direction Y.
“TEMP_GRAD_Z” corresponds to a gradient in direction Z.
Several main Bulk Data Files defined in “MAINS” directory are provided to allow the testing of result importations for different Nastran solution sequences:
“sol103.bdf” presents an example of Real modal analysis (SOL103).
“sol105.bdf” presents an example of buckling analysis (SOL105).
“sol106.bdf” presents an example of non-linear analysis (SOL106).
“sol111_mp_xyz.bdf” presents an example of dynamic response analysis with a SOL111 solution sequence and with Complex Results output in magnitude-phase format.
“sol111_ri_xyz.bdf” presents an example of dynamic response analysis with a SOL111 solution sequence and with Complex Results output in real-imaginary format.
“sol200_a.bdf” corresponds to an optimization with design variables.
“sol200_b.bdf” corresponds to a topometric optimization.
“sol400.bdf” for a non-linear analysis with “SOL 400” solution sequence.
One gives here information on the way the model has been split into several files and the organization of the files into different directories.
The files are located in six different directories:
The directory “MAINS” contains the main data files that are used for Nastran calculations. The “main” files define various execution parameters, the load cases,... They also include model files located in other directories. The main files have a “.bdf” extension.
All files defining materials (“MAT*” cards) are located in “MATS” directory. All these files have a “.bdf” extension.
All files defining property cards are defined in “PROPS” directory. All these files have a “.bdf” extension.
In directory “FIXAS”, one places the files that define fixations of the structure. All these files have a “.bdf” extension.
In directory “LOADS” are the files that define loads applied to the structure. These loads may include local forces, quasi-static loads, temperature fields for thermo-elastic calculations,...
In directory “MESH” are located all the elements defining the structure, its internal connections, its GRIDS, its coordinate systems,... This is normally the largest directory. Note that one makes the distinction between the internal connections modeled with RBE2 elements, and their CBAR version for thermo-elastic calculations.
In directory “EXEC_OP2”, the main bdf files should be copied. (Actually, they already have been copied in the directory.) This is the directory in which the Nastran runs should be done. Otherwise, it is also possible to make the calculations elsewhere. But then, the examples should be modified, or symbolic links will have to be created.
In directory “EXEC_XDB”, one finds the same bdf files as in “EXEC_OP2” directory except that in each file the line “PARAM POST -1” as been replace by “PARAM POST 0”. This ensures that an xdb Result file shall be produced instead of an op2. The remarks done for directory “EXEC_OP2” apply to directory “EXEC_XDB”.
Note also that each file include in a “.bdf” main data file can itself include other files.
The directory “PATRAN” contains a Patran session file that can be used to import the definition of groups in a Patran or FeResPost DataBase.
In this Chapter, one presents very small examples of data files performing simple operations with the FE model and Results. This allows to familiarize the reader to the use of FeResPost, and possibly to ruby also.
The examples are divided four categories:
Section IV.2.1 presents the “Util” Module that is used in several of the examples.
Section IV.2.2 shows how the model is read from a Bulk Data File and how Groups can be manipulated. No Results are considered in those examples.
Section IV.2.3 shows how some iterators are used.
Section IV.2.4 is more specifically devoted to the manipulation of Results.
In section IV.2.5, one presents two useful tools that can be used to generate loads for subsequent Nastran calculations.
In file“"RUBY/UTIL/util.rb”, one defines the “Util” Module that contains several useful methods:
“printRes” outputs a formatted listing of one Result object. The three argument of the method are an output stream, a title name for the listing and the Result object to be printed.
“printGrp” outputs a summary of information on a Group. The three argument of the method are an output stream, a title name for the listing and the Group object.
“printDbResList” outputs a listing with the characteristics of all the Results stored in a DataBase object. The two arguments are an output stream and a DataBase object.
“printDbGrpList” outputs a listing with the characteristics of all the Groups stored in a DataBase object. The two arguments are an output stream and a DataBase object.
One presents here several examples illustrating the manipulation of Groups in FeResPost. They show how the Groups defined in the DataBase can be inspected, and how new Groups can be constructed and added to the DataBase.
The first example illustrates different versions of the call to “readBdf” method:
require "FeResPost"
include FeResPost
# Creates and initializes the DataBase :
db=NastranDb.new()
db.Name="tmpDB1"
db.readBdf("../../MODEL/MAINS/unit_xyz.bdf")
The first call to “readBdf” is the default instruction used to read the Bulk file in most examples.
A second bdf read operation is performed as follows:
db=NastranDb.new()
db.Name="tmpDB2"
begin
db.readBdf("unit_xyz_V1.bdf",[],"bdf",{},true)
rescue Exception => x then
printf ("\n\nMaybe you should modify the two first include statements in main file!\n")
printf ("**********************************************************************\n\n")
raise x
end
The revised version reads main file “unit_xyz_V1.bdf” that illustrates several possible interpretation of the “include” statements in Nastran Bulk Data Files. The user must uncomment the corresponding statement, and modify the absolute paths in the include statements of “unit_xyz_V1.bdf” file. (The “begin” and “rescue” statements have been added to remind the user of this necessary modification. An error message is issued if the reading fails.)
Include statement in the data file look as follows:
include ’/home/ferespost/Documents/FERESPOST/TESTSAT/ MODEL/MESH/coordSys.bdf’ include /home/ferespost/Documents/FERESPOST/ , TESTSAT/MODEL/MATS/mats.bdf include ’../../MODEL/PROPS/props.bdf’ $ include ../../MODEL/MESH/elemNodes_pan_MX.bdf include ../../MODEL/MESH/elemNodes_pan_MY.bdf include ../../MODEL/MESH/elemNodes_pan_MZ.bdf include ../../ MODEL/MES H/elemNod es_pan_PX.bdf include ../../MODEL/MESH/ elemNodes_pan_PY.bdf
The example is given in file “RUBY/EX01/readBdf.rb”.
Another version of the example is given in file “RUBY/EX01/readBdf_V2.rb”. It illustrates the reading of Bulk Data Files containing include statements in which symbols are used. In that example, the call to “readBdf” looks as follows:
symbols=Hash.new
symbols["INCDIR"]="../../MODEL"
db=NastranDb.new()
db.Name="tmpDB2"
db.readBdf("unit_xyz_V2.bdf",[],"bdf",symbols,true)
The variable “symbols” is a Hash containing the list of symbols that must be substituted in the include statements. (Only one symbol is defined in this case.) The include statements of the BDF file look as follows:
include INCDIR:/MESH/elemNodes_pan_MX.bdf include INCDIR:/MESH/elemNodes_pan_MY.bdf include INCDIR:/MESH/elemNodes_pan_MZ.bdf include ../../ MODEL/MES H/elemNod es_pan_PX.bdf include INCDIR:/MESH/ elemNodes_pan_PY.bdf
The example “readBdf_V3” proposes a slightly more complicated case of file inclusions in a main BDF.
In Example “readBdf_V7” one proposes to illustrate several functions allowing the manipulation of the database FEM entities. A list of Nastran cards corresponding to the FEM definition is build as follows:
cards=[]
db.each_coordSysId do |id|
cards << db.fillCard("CoordSys",id)
end
db.each_nodeId do |id|
cards << db.fillCard("Node",id)
end
db.each_elemId do |id|
cards << db.fillCard("Element",id)
end
db.each_rbeId do |id|
cards << db.fillCard("RBE",id)
end
db.each_materialId do |id|
cards << db.fillCard("Material",id)
end
db.each_propertyId do |id|
cards << db.fillCard("Property",id)
end
Then, one builds a new database using these cards:
db3=NastranDb.new() db3.Name="tmpDB3" db3.insertCards(cards);
Finally, one checks the content of the new database:
db3.writeBdfLines("out.bdf","w","left","short","All");
vectStr=NastranDb.writeNastranCardsToVectStr("left","short",cards);
vectStr.each do |line|
puts line
end
Example “readBdf_V8” illustrates the reading of a model by several calls to “readBdf” methods:
db.readBdf("D:/SHARED/FERESPOST/TESTSAT/MODEL/MESH/coordSys.bdf",nil,nil,nil,true,true)
db.readBdf("D:/SHARED/FERESPOST/TESTSAT/MODEL/MATS/mats.bdf",nil,nil,nil,true,true)
db.readBdf("../../MODEL/PROPS/props.bdf",nil,nil,nil,true,true)
...
db.readBdf("../../MODEL/FIXAS/launch.bdf",nil,nil,nil,true,true)
db.readBdf("../../MODEL/LOADS/unit_accel.bdf",nil,nil,nil,true,true)
This approach can be used to modify finite element model stored in a database during script execution.
It shows how it is possible to obtain the list of Groups contained in a DataBase. This may be useful if one wants to check whether all Groups read from a session file have been correctly integrated in the DataBase. The ruby program looks like:
# Creates and initializes the DataBase :
db=NastranDb.new()
db.Name="tmpDB"
db.readBdf("../../MODEL/MAINS/unit_xyz.bdf")
db.readGroupsFromPatranSession("../../MODEL/PATRAN/groups.ses")
# Prints all the group names :
puts db.getAllGroupNames()
The last line performs the printing of the names of all Groups contained in the DataBase. The other lines are for DataBase creation and initialization.
The example is given in file "RUBY/EX02/printGroupNames.rb".
In the previous example one simply printed the list of the names of Groups contained in a DataBase. In this new examples, one also print information on the content of each Group. Practically, this is done as follows:
One initializes the DataBase “as usual”.
One loops on the list of Group names stored in the DataBase, and for each groupName:
One gets a copy of the Group stored in the DataBase.
For the four types of entities one recovers the entities. Actually, one only stores the respective sizes of the Arrays returned by the call to “getEntitiesByType”.
Finally, one prints the result (formatted print).
The program looks like this:
# Creates and initializes the DataBase :
db=NastranDb.new()
db.Name="tmpDB"
db.readBdf("../../MODEL/MAINS/unit_xyz.bdf")
db.readGroupsFromPatranSession("../../MODEL/PATRAN/groups.ses")
# Prints Groups’ data :
printf("%20s%10s%10s%10s%10s\n","groupName","Nodes",\
"Elements","RBEss","CoordSys")
db.each_groupName do |groupName|
grp = db.getGroupCopy(groupName)
nodesNbr = grp.NbrElements
elementsNbr = grp.NbrNodes
rbesNbr = grp.NbrRbes
coordNbr = grp.NbrCoordsys
printf("%20s%10d%10d%10d%10d\n",groupName,nodesNbr,\
elementsNbr,rbessNbr,coordNbr)
end
The example is given in file "RUBY/EX02/printGroups.rb".
The third example prints Groups defined in a Patran session file without importing them into a DataBase. Groups are directly read into a Hash object with the following statement:
h=Post.readGroupsFromPatranSession("../../MODEL/PATRAN/groups.ses")
Then, for each Group, the entities are printed as lists of integer. One shows below how it is done for the nodes:
nbrEntitiesPerLine=8
h.each do |id,grp|
os.printf("Group \"%s\":\n\n",id)
...
nbr=grp.getNbrEntitiesByType("Node")
os.printf(" Nbr Nodes: %d",nbr)
counter=0
grp.each_node do |id|
if (counter%nbrEntitiesPerLine==0) then
os.printf("\n ")
end
os.printf("%8d",id)
counter+=1
end
os.printf("\n\n")
...
end
The example is given in file "RUBY/EX02/writeGroupEntities.rb".
The entities stored in a Group can be manipulated. For example, the following statements:
grpList=[]
grp=Group.new
grp.addEntities("Element 20000:24999 Node 20000:24999")
grp.Name="pan_MX"
grp.matchWithDbEntities(db)
grpList << grp
create a Group, add elements and nodes into it, remove the elements and nodes undefined in the db DataBase and insert the created Group into an Array.
It is also possible to add or remove entities with range defined with steps:
grp=Group.new
grp.addEntities("Element 20000:24999:7 Node 20000:24999:7")
grp.removeEntities("Element 20000:24999:28 Node 20000:24999:28")
grp.Name="pan_MX_7_28"
grp.matchWithDbEntities(db)
grpList << grp
At the end of the example, the Groups are saved into a Patran session file:
Post::writeGroupsToPatranSession("groups.ses",grpList)
The example is given in file "RUBY/EX03/manipGroups.rb".
In the examples of section IV.2.2.2, one initialized a DataBase and examined its Groups and the content of the Groups. In this example, one shows how the Groups can be manipulated, and the DataBase modified during the execution of the program.
The groups contained in session file “groups.ses” are not sufficient to suit our post-processing requirements. Indeed, it would be very practical if for each panel, a distinction between the skins and honeycomb could be made. We decide that it shall be done by adding new Groups to the DataBase. This problem can be solved in four steps:
Initialization of a DataBase.
Creation of Groups by association to materials.
Creation of Groups by intersections and insertion in the DataBase.
Printing of the Groups contained in the DataBase (for checking the result of the operation).
Steps 1 and 4 above correspond to the operation of the example presented in section IV.2.2.2. Therefore, one does not present those parts of the program here. One only gives explanation on steps 2 and 3.
The creation of “material Groups” is done by calling the DataBase “getElementsAssociatedToMaterialId” method. Three Groups are created, corresponding to honeycomb 50 , honeycomb 72 and Aluminum 2024 T3 respectively. Practically this is programmed as follows:
# Groups created by Materials : tmpGroup_Honey_50 = db.getElementsAssociatedToMaterialId(5) tmpGroup_Honey_50 += db.getElementsAssociatedToMaterialId(4) tmpGroup_Honey_50.Name="Honey_50" tmpGroup_Honey_72 = db.getElementsAssociatedToMaterialId(6) tmpGroup_Honey_72.Name="Honey_72" tmpGroup_Al_2024 = db.getElementsAssociatedToMaterialId(3) tmpGroup_Al_2024.Name="Al_2024" tmpGroup_CFRP = db.getElementsAssociatedToMaterials(10000) tmpGroup_CFRP.Name="CFRP" matGroups = Array.new() matGroups << tmpGroup_Honey_50 matGroups << tmpGroup_Honey_72 matGroups << tmpGroup_Al_2024 matGroups << tmpGroup_CFRP db.addGroupCopy(tmpGroup_Honey_50) db.addGroupCopy(tmpGroup_Honey_72) db.addGroupCopy(tmpGroup_Al_2024) db.addGroupCopy(tmpGroup_CFRP)
One can make a few remarks about the previous ruby lines:
The integer identifiers of the various materials are described in section IV.1.2.
For the honeycomb 50 , the Group is created in two steps because two corresponding materials have been defined: one MAT8 and one MAT9. The MAT8 corresponds to the -Z panel which is modeled with surface elements. There is no corresponding duplication for Aluminum 2024 material which is isotropic (MAT1).
After being created, the material Groups are stored in an Array called “matGroups”. This storage simplifies the creation of the Groups by intersection at step 3.
The three Groups are stored in the DataBase. This operation has no peculiar utility in this example and could be cancelled.
After the creation of material Groups, one creates the other Groups by intersection (step 3). This is done as follows:
# Groups created by intersection :
panelGroupNames = Array.new()
panelGroupNames << "pan_MX"
panelGroupNames << "pan_MY"
panelGroupNames << "pan_MZ"
panelGroupNames << "pan_PX"
panelGroupNames << "pan_PY"
panelGroupNames << "pan_PZ"
panelGroupNames << "pan_SUP"
for panelGroupName in panelGroupNames
panelGroup = db.getGroupCopy(panelGroupName)
for matGrp in matGroups
newGrp = panelGroup * matGrp
newGrp.Name=panelGroupName+"_"+matGrp.Name
if newGrp.getEntitiesByType("Element").size > 0
db.addGroupCopy(newGrp)
end
end
end
Here again, a few commentaries can be done:
“panelGroupNames”, an Array containing the names of the Groups corresponding to the different sandwich panels is constructed explicitly.
A “for” loop is nested into another “for” loop. The external one is the loop on the panel Group names, and the internal one is the loop on the material Groups.
In the external loop, one asks to the DataBase a copy of The Group with the appropriate name.
In the internal loop, on performs the intersection operations. Each Group is stored in variable newGroup. It is named with a String obtained by concatenation of the names of intersected Groups. Then it is inserted in the DataBase only if it contains entities.
The example is given in file “RUBY/EX03/makeMatGroups.rb”.
One presents one example illustrating the use of some of the iterators defined in DataBase class. The following lines print the elements connectivity:
db.each_elemId do |elemId|
STDOUT.printf(" %d =>",elemId)
db.each_nodeOfElement(elemId) do |nodeId|
STDOUT.printf(" %d",nodeId)
end
STDOUT.printf("\n")
end
Two iterators have been used in the calculation: “each_elemId” and “each_nodeOfElement”. A second version of the loop restricts the printing of connectivity to corner nodes only.
The example is given in file “RUBY/EX16/elemConnectivity.rb”.
An iterator is also used in example “RUBY/EX03/properties.rb”. In that example, one uses the “fillCard” method of NastranDb class to obtain the definition of the properties in the model:
db.each_propertyId do |id|
puts "Property",id
card=db.fillCard("Property",id)
puts card
end
(See section III.1.1.5 for the definition of “fillCard” method.)
The following example prints the information on Results available in the DataBase. It starts with the following lines:
require "FeResPost"
include FeResPost
#DataBase::disableLayeredResultsReading
#DataBase::disableSubLayersReading("Bottom")
#DataBase::disableSubLayersReading("Mid")
#DataBase::disableSubLayersReading("Top")
The commented lines are methods that disable partially or entirely the reading of composite element layered Results. After reading the corresponding manual in section I.1.3.2, you may un-comment some of these instructions to check the effect on the reading of composite Results.
The main part of the example program looks like this:
# Reading or generating Results :
db.readOp2("../../MODEL/EXEC_OP2/unit_xyz.op2","Results")
db.generateCoordResults
db.generateCoordResults("Fake Coords Case","No SubCase","coords")
# Inspecting and reading Results :
db.each_resultKeyCaseId do |lcName|
printf("LOADCASE: \"%s\"\n",lcName)
end
db.each_resultKeySubCaseId do |scName|
printf("SUBCASE: \"%s\"\n",scName)
end
db.each_resultKeyLcScId do |lcName,scName|
printf("LOADCASE and SUBCASE: \"%s\" - \"%s\"\n",lcName,scName)
end
db.each_resultKeyResId do |resName|
printf("RESULT: \"%s\"\n",resName)
end
db.each_resultKey do |lcName,scName,tpName|
tmpRes=db.getResultCopy(lcName,scName,tpName)
printf("%-20s%-15s%-50s%-10d\n",lcName,scName,tpName,\
tmpRes.Size)
end
It works as follows:
The call to method “readOp2” loads Results into the DataBase.
One also generate coordinate Results.
Then one builds three lists containing the load cases, sub cases and type names of all the Results contained in the DataBase. Those are three Array of String objects. Their respective contents are printed.
One uses several iterators that read the lists of load cases, subcases and Result identifiers and prints the output.
Using the iterator “each_resultKey” one obtains copy of the Results stored in the DataBase, prints the corresponding key identifiers, and the corresponding size.
The example is provided in file “RUBY/EX04/printResLists.rb”.
Another example illustrating the reading of Results from a Nastran OP2 file is provided in file “RUBY/EX04/printResLists_filter.rb”. This example illustrates the use of “readOp2FilteredResults” method.
One shows here how calculations can be performed with Result objects. One first initializes the DataBase and imports Results with function “readOp2”. In this example, one works with the thermo-elastic version of the model, but its initialization is vey similar to the initialization in other examples. One also add addition Groups corresponding to skins and honeycomb of the sandwich panels, like in the example of section IV.2.2.4. Those parts are not described here.
One first describes the manipulation of results that lead to the calculation of maximum equivalent Von Mises stress in the skins of upper panel. The corresponding ruby lines look like this:
targetGrp = db.getGroupCopy("pan_PZ_Al_2024")
stress = db.getResultCopy("ORBIT_ONE_MS2_Z","Statics",\
"Stress Tensor","ElemCorners",targetGrp,[])
scalar = stress.deriveTensorToOneScal("VonMises")
maxScalar = scalar.extractResultMax
maxRkl = maxScalar.extractRkl
maxStress = stress.extractResultOnRkl(maxRkl)
maxScalarData = maxScalar.getData()[0]
maxStressData = maxStress.getData()[0]
puts
puts "Maximum Von Mises stress in panel +Z skins :"
puts
printf(" %.2f Pa on element %d (layer=\"%s\").\n",
maxScalarData[5],maxScalarData[0],maxScalarData[2])
printf(" Sxx = %.2f, Syy = %.2f, Szz = %.2f,\n",maxStressData[5],\
maxStressData[6],maxStressData[7])
printf(" Sxy = %.2f, Syz = %.2f, Szx = %.2f\n",maxStressData[8],\
maxStressData[9],maxStressData[10])
Basically, the process can be divided into three parts:
Actual calculation of Von Mises stress. One recovers the Cauchy stress tensor corresponding to the selected load case and selected Group. Then one derives a scalar equivalent Von Mises stress.
Selection of the data corresponding to the maximum Von Mises stress. This is done as follows:
First, a call to “extractResultMax” is done to build a Result object containing the maximum Von Mises stress.
Then one recovers the ResKeyList object corresponding to this maximum stress. The ResKeyList object contains only one Result key.
One recovers the Cauchy stress tensor corresponding to the maximum stress.
Finally, one recovers the values contained in the selected maximum equivalent Von Mises stress and corresponding Cauchy stress values. Remark the “[0]” at the end of calls to “getData” methods. The reader must remember that this method returns an Array of Arrays. But in this particular case, the returned Array has only one Array element.
Printing of the Results. The reader will understand by himself how it works.
In the same file, one also calculates a maximum out of plane shear stress in the honeycomb of the +Z panel. The calculation of this stress is done as follows:
targetGrp = db.getGroupCopy("pan_PZ_Honey_72")
stress = db.getResultCopy("ORBIT_ONE_MS2_Z","Statics",\
"Stress Tensor","ElemCorners",targetGrp,[])
sXZ = stress.deriveTensorToOneScal("Component XZ")
sYZ = stress.deriveTensorToOneScal("Component YZ")
scalar = Post.sqrt(sXZ*sXZ+sYZ*sYZ)
Similarly, one calculates the “MaxShear” stress (obtained from the eigen values of the Cauchy stress tensor):
targetGrp = db.getGroupCopy("pan_PZ_Honey_72")
stress = db.getResultCopy("ORBIT_ONE_MS2_Z","Statics",\
"Stress Tensor","ElemCorners",targetGrp,[])
scalar = stress.deriveTensorToOneScal("MaxShear")
In the same data file, one shows how the bar stresses are recovered:
targetGrp = db.getGroupCopy("strut_A")
stress = db.getResultCopy("ORBIT_ONE_MS2_X","Statics",\
"Beam Axial Stress for Bending Loads","ElemCorners",targetGrp,[])
scalar = Post.abs(stress)
maxScalar = scalar.extractResultMax
maxRkl = maxScalar.extractRkl
maxStress = stress.extractResultOnRkl(maxRkl)
maxScalarData = maxScalar.getData()[0]
maxStressData = maxStress.getData()[0]
puts
puts "Maximum bar stress in strut A :"
puts
printf(" %.2f Pa on element %d (layer=\"%s\").\n",
maxScalarData[5],maxScalarData[0],maxScalarData[2])
printf(" Sxx = %.2f\n",maxStressData[5])
puts
puts
Note that the way maximum stress is recovered from FE Results is different because Nastran calculates only the longitudinal component of the stress tensor at four locations in the cross-section. The shear stress is not taken into account in this calculation. More complicated calculations have to be performed to take into account all the components of the stress tensor for bar and beam elements.
These examples are provided in file “RUBY/EX05/printStressMax.rb”. Another example illustrating the calculation of tensorial results eigen-values and eigen-vectors is presented in file “RUBY/EX05/eigenQR.rb”.
The example given in file “RUBY/EX05/calcHoneyAccel.rb” explains how a predfined criterion can be calculated. This is done for the “HoneycombAirbusSR” predefined criterion presented in detail in section X.D.1.2. The operations can be sorted in three steps:
First the Cauchy Stress Tensor Result is extracted fro a Group of elements:
targetGrp = db.getGroupCopy("pan_PZ_Honey_72")
stress = db.getResultCopy("ORBIT_ONE_MS2_Z","Statics","Stress Tensor",
"ElemCorners",targetGrp,[])
Then an Array of parameters is prepared:
criterionData=[]
criterionData << db
criterionData << 1.5625
criterionData << 2.41e6
criterionData << 1.41e6
criterionData << "XZ"
criterionData << "YZ"
criterionData << stress
(The reader will easily check that these parameters correspond to those liste in section X.D.1.2.
The criterion is calculated by a call to “Post.calcPredefinedCriterion” method:
output=Post.calcPredefinedCriterion("HoneycombAirbusSR",criterionData)
Finally, the “output” Array returned by the method is exploited:
puts
puts "Worst results in panel +Z honeycomb :"
puts
STDOUT.printf(" on element %d\n",output[0])
STDOUT.printf(" on node %d\n",output[1])
STDOUT.printf(" on layer %d\n",output[2])
STDOUT.printf(" on sub-layer %d\n",output[3])
STDOUT.printf(" SL = %g\n",output[4])
STDOUT.printf(" SW = %g\n",output[5])
STDOUT.printf(" SR max = %g\n",output[6])
puts
Util.printRes(STDOUT,"Honey SR",output[7])
In this case, the “exploitation” consists simply in prints to standard output.
Note that the seventh element of the “output” Array above is the only Result object created and returned by the predefined criterion. The same object could be obtained by a few ruby statements like:
shearL=@@stressTensor.deriveTensorToOneScal("Component XZ")
shearW=@@stressTensor.deriveTensorToOneScal("Component YZ")
tmp=sq(shearL/allL)+sq(shearW/allW)
sr=fos*sqrt(tmp)
The computational cost of these few statement can be very important however. Indeed, several FeResPost Result objects are created by these few lines. One creates consecutively the following result objects:
One “shearL” scalar Result by extraction of XZ component.
One “shearW” scalar Result by extraction of YZ component.
One “shearL/allL” scalar Result (division by real value).
One “shearW/allW” scalar Result (division by real value).
One “sq(shearL/allL)” scalar Result (scalar Result to the square).
One “sq(shearW/allW)” scalar Result (scalar Result to the square).
One “tmp” Result obtained by summation of two scalar Results.
One “sqrt(tmp)” Result obtaiend by extracting the square root of a scalar Result.
And finally, the “sr” Result, which is the only one that shall be kept.
This means that 8 intermediate Result objects have been created and are discared at the end. Each of the 8 intermediate Result creation involves a loop on all the key-value pairs of the operations argument(s), and insertion in the new Result. If the initial Cauchy Stress Tensor Result contains a large number of key-value pairs, the computation cost of this criterion can be very important.
In the same ruby file, one provides a second computation of the Airbus criterion using the “interaction” approach:
lStress=stress.deriveTensorToOneScal("Component XZ")
wStress=stress.deriveTensorToOneScal("Component YZ")
criterionData=[]
criterionData << Post.abs(lStress)*(1.5625/2.41e6)
criterionData << 2.0
criterionData << Post.abs(wStress)*(1.5625/1.41e6)
criterionData << 2.0
#~ output=Post.calcPredefinedCriterion("Interaction_2_SR",criterionData)
output=Post.calcPredefinedCriterion("Interaction_N_SR",criterionData)
srMax=output[1].extractResultMax()
maxData=srMax.getData("int","int","int","int","int")[0];
Of couse, this calculation method is less efficient than the previous one. It illustrates however the calculation of Strength Ratios via interaction of failure criteria.
One presents here an example in which Results corresponding to the STRAIN Nastran output statement are printed. Note that the non-diagonal components of the Nastran tensors corresponding to STRAIN statement are multiplied by two by Nastran. So, when imported into a DataBase, one divides the corresponding components by two (see remark 5 page 654 in Chapter III.1).
The preliminary part of the program is similar to the previous one: one initializes a DataBase, imports a Nastran model, produces the Groups and read Results. Then, the strain tensor in the honeycomb of +Z panel is output. This is done as follows:
targetGrp = db.getGroupCopy("pan_PZ_Honey_72")
strain = db.getResultCopy("TEMP_GRAD_X","Statics",\
"Strain Tensor","ElemCenters",targetGrp,[])
puts
puts "Strain tensor in panel +Z honeycomb :"
puts
strain.each("int","int","int") do |key,values|
for j in 0..3
printf("%10s",key[j].to_s)
end
if (values[0]) then
printf("%10s",values[0].to_s)
else
printf("%10s","nil")
end
for j in 1..6
printf("%14f",values[j])
end
printf("\n")
end
The "each" iterator is used with three "int" parameters. This leads to a printed output in which the layers are output with integer values.
In surface elements, two Results correspond to the STRAIN Nastran output statement: the strain tensor and the curvature tensor. The way components of the strain tensor are printed is similar as for the honeycomb. For the curvature tensor, the print is done as follows:
targetGrp = db.getGroupCopy("pan_PZ_Al_2024")
strain = db.getResultCopy("TEMP_GRAD_X","Statics",\
"Strain Tensor","ElemCenters",targetGrp,[])
puts
puts "Strain tensor in panel +Z skins :"
puts
strain.each do |key,values|
for j in 0..3
printf("%10s",key[j].to_s)
end
if (values[0]) then
printf("%10s",values[0].to_s)
else
printf("%10s","nil")
end
for j in 1..6
printf("%14f",values[j])
end
printf("\n")
end
This example is provided in file "RUBY/EX08/printStrain.rb".
Similarly, one print Results corresponding to Forces and Moments in CBAR elements. The interesting part is given below:
targetGrp = db.getGroupAllFEM
forces = db.getResultCopy("LAUNCH_ONE_MS2_X","Statics",\
"Beam Forces","Elements",targetGrp,[])
moments = db.getResultCopy("LAUNCH_ONE_MS2_X","Statics",\
"Beam Moments","Elements",targetGrp,[])
Util::printRes(STDOUT,"Forces",forces)
Util::printRes(STDOUT,"Moments",moments)
The reader will observe in Results that “Beam Forces” in CBAR elements are given at the center of elements only, while “Beam Moments” are printed at the two end nodes of each element.
This example is provided in file "RUBY/EX08/printBeamForces.rb".
One first presents an example, in which one modifies the coordinates of a point, and the components of a vector and of a tensor attached to this point. One first extracts the coordinate systems that are used in this example, and one defines the entities that shall be transformed:
cs5=db.getCoordSysCopy(5) cs6=db.getCoordSysCopy(6) x=[5.0,0.0,0.0] v=[1.5,3.2,-4.0] m=[[2.0,3.0,-7.0],[1.0,0.0,0.0],[0.0,0.0,1.0]]
One assumes that the coordinates and components of the vector and tensor defined above are given in coordinate system 5. Coordinates and components can be expressed in basic coordinate system as follows:
x0=cs5.changeCoordsA20(x) v0=cs5.changeCompsA20(x,v) m0=cs5.changeCompsA20(x,m)
Then, the coordinates and components can be re-expressed wrt coordinate system 5 using the following transformations:
x5=cs5.changeCoords02B(x0) v5=cs5.changeComps02B(x0,v0) m5=cs5.changeComps02B(x0,m0)
Coordinates and components can also be transformed directly from coordinate system 5 to 6:
x6=cs5.changeCoordsA2B(x5,cs6) v6=cs5.changeCompsA2B(x5,v5,cs6) m6=cs5.changeCompsA2B(x5,m5,cs6)
and then back to coordinate system 5:
x5=cs6.changeCoordsA2B(x6,cs5) v5=cs6.changeCompsA2B(x6,v6,cs5) m5=cs6.changeCompsA2B(x6,m6,cs5)
The entire example is given in file "RUBY/EX09/modifCS.rb".
One presents below an example that illustrates the transformations of coordinate system in which Result components are expressed. One loads results on elements with PCOMP properties. Then the components are printed after several transformations:
Native results as stored in the “op2” file. These results are given in the ply local coordinate system.
Results in the element IJK coordinate system (Patran element coordinate system).
Results given in DataBase defined Cartesian coordinate system number 7.
Results given in material coordinate system.
Results given in projected coordinate system 0.X.
Results given in projected coordinate system 0.Y.
Results given in element local (Nastran) coordinate system.
The transformations are performed with the following instructions:
... stress.modifyRefCoordSys(db,0) ... stress.modifyRefCoordSys(db,"elemIJK") ... stress.modifyRefCoordSys(db,7) ... stress.modifyRefCoordSys(db,"matCS") ... stress.modifyRefCoordSys(db,0,[1.0, 0.0, 0.0]) ... stress.modifyRefCoordSys(db,0,[0.0, 1.0, 0.0]) ... stress.modifyRefCoordSys(db,"elemCS") ...
Two versions of the sequence of transformations are proposed:
In the first version, the transformations are done from the native Results. This means that the Result object to be transformed is reloaded from the DataBase prior to each transformation. One also presents an example of use of the “each” iterator of Result class.
In the second version, the transformation is done successively on the same Result object which has been loaded only once. One also presents examples of the use of “each”, “each_key” and “each_values” of the Result class. For example, two versions of the use of “each_key” iterator are presented:
...
stress.each_key do |stressKey|
for j in 0..3
printf("%10s",stressKey[j].to_s)
end
printf("\n")
end
stress.each_key("int","int","int","int") do |elemId,nodeId,layerId,subLayerId|
printf("%10s",elemId.to_s)
printf("%10s",nodeId.to_s)
printf("%10s",layerId.to_s)
printf("%10s",subLayerId.to_s)
printf("\n")
end
...
The example ends with an error message for the second version because it is not possible to transform a Result object if stored values are already expressed in a projected coordinate system.
This example is provided in file "RUBY/EX09/modifCS2D.rb". A second version of the example with transformation of results on 3D elements is given in file "RUBY/EX09/modifCS3D.rb".
A third version involving the use of user defined coordinate systems is provided in file "RUBY/EX09/modifCS2Db.rb". This version illustrate the manipulation of CoordSys objects.
Finally, a fourth version of the 2D example is obtained by addition new arguments to the “modifyRefCoordSys” method in such a way that Results expressed in user or projected coordinate systems can further be modified without resulting in error messages. The successive transformation of coordinate systems become:
... stress.modifyRefCoordSys(db,0) ... stress.modifyRefCoordSys(db,"elemIJK") ... stress.modifyRefCoordSys(db,7) ... stress.modifyRefCoordSys(db,"matCS") ... stress.modifyRefCoordSys(db,0,[1.0, 0.0, 0.0]) ... stress.modifyRefCoordSys(db,0,[0.0, 1.0, 0.0],0,[1.0, 0.0, 0.0]) ... stress.modifyRefCoordSys(db,"elemCS",nil,0,[0.0, 1.0, 0.0]) ...
This last version is given in file "RUBY/EX09/modifCS2Dc.rb".
Finally, one proposes in "RUBY/EX09/modifCS2Dd.rb" a version of the example in which a “FieldCS” Result is used to modify the components of stress tensor. The FieldCS Result is defined as follows, from the stress tensor Result:
fldCS=Result.new() fldCS.Format=1 fldCS.TensorOrder=-10 fldCS.insertRklVals(stress,[5,1.0,0.0,0.0,0.0,1.0,0.0,0.0,0.0,1.0]) fldCS.modifyRefCoordSys(db,0)
(Note that the FieldCS is often constructed from the Result object of which it is meant to modify the components by calling modifyRefCoordSys mehtod.) The “fieldCS” Result is then simply used in a coordinate system transformation as follows:
... when 3 then puts puts "FieldCS" puts stress.modifyRefCoordSys(db,fldCS) ...
In this example, Complex Results will be read from a Nastran xdb file. One first examines the information stored in the result file, in order to extract only the Results on needs to illustrate the manipulation of Complex Results.
The part of interest looks as follows:
xdbFileName="../../MODEL/EXEC_XDB/sol111_ri_xyz.xdb" tab=NastranDb.getXdbLcScResNames(xdbFileName) lcNames=tab[0] scNames=tab[1] resNames=tab[2]
The lists of load cases, sub-cases and result types stored in the xdb file are saved into three Arrays of Strings that can be printed or used for other purposes.
The part of interest looks as follows:
xdbFileName="../../MODEL/EXEC_XDB/sol111_ri_xyz.xdb"
infos=NastranDb.getXdbLcInfos(xdbFileName)
infos.each do |tab|
STDOUT.printf("%-20s %-25s %-6d %-6d %-15g %-15g\n",
tab[0],tab[1],tab[3],tab[4],tab[5],tab[6])
end
One extracts the information about the load cases and sub-cases to which Results are associated in the xdb file. Then, the name of load cases, sub-cases and associated integer and real data are printed. (Note, that the third String ID, which is always void, is not printed.) The example is provided in file "RUBY/EX17/printXdbLcInfos.rb".
The results of "printXdbLcInfos.rb" are used to select load cases and sub-cases for which Results are imported into the DataBase. One also selects some of the Results:
lcNames=[] lcNames << "SINUS_X" scNames=[] scNames << "Output 70 (f = 119.0000)" scNames << "Output 30 (f = 79.0000)" scNames << "Output 1 (f = 50.0000)" resNames=[] resNames << "Accelerations, translational (MP)" resNames << "MPC Forces, Forces (MP)" resNames << "MPC Forces, Moments (MP)" resNames << "Accelerations, translational (RI)" resNames << "MPC Forces, Forces (RI)" resNames << "MPC Forces, Moments (RI)"
Note that the selection of sub-cases to be imported into the DataBase is useful even when all the load cases are to be post-processed. Indeed the post-processing of a limited number of load cases at the same time reduces the amount of memory required to store all the Results. However, this means that several Result importations might be necessary, and this increases the time needed for disk IO operations.
Then the results are imported from xdb files corresponding to SOL111 Nastran calculations. One reads two files: one in which the Results are saved in rectangular format, and one in which they are saved in polar format:
xdbFileName="../../MODEL/EXEC_XDB/sol111_ri_xyz.xdb" db.readXdb(xdbFileName,lcNames,scNames,resNames) xdbFileName="../../MODEL/EXEC_XDB/sol111_mp_xyz.xdb" db.readXdb(xdbFileName,lcNames,scNames,resNames)
To illustrate the manipulation of Results, the extraction is done for one particular load case, one particular sub-case, and on a small Group of 11 nodes only:
tmpGroup=Group.new
tmpGroup.setEntities("Node 60100:60110")
lcName="SINUS_X"
scName="Output 30 (f = 79.0000)"
Only the “Accelerations” Result is studied:
resRI=db.getResultCopy(lcName,scName,"Accelerations, translational (RI)", "Nodes",tmpGroup,[]) Util::printRes(STDOUT,"Accelerations resRI",resRI) resMP=db.getResultCopy(lcName,scName,"Accelerations, translational (MP)", "Nodes",tmpGroup,[]) Util::printRes(STDOUT,"Accelerations resMP",resMP)
The following statements illustrate the polar-rectangular formats conversions:
calcMP=Result.new calcMP.set2MP(resRI) Util::printRes(STDOUT,"Accelerations calcMP",calcMP) calcRI=Result.new calcRI.set2RI(resMP) Util::printRes(STDOUT,"Accelerations calcRI",calcRI)
And here, one shows how Real Results can be extracted from complex ones:
resR=calcMP.getR resM=calcMP.getM resI=calcMP.getI resP=calcMP.getP Util::printRes(STDOUT,"Accelerations resR",resR) Util::printRes(STDOUT,"Accelerations resM",resM) Util::printRes(STDOUT,"Accelerations resI",resI) Util::printRes(STDOUT,"Accelerations resP",resP)
Of course, the reverse operation can be done too. Here is how Complex Results can be assembled from one pair of Real Results:
assyRI=Result.new assyMP=Result.new assyRI.assembleComplex(2,resR,resI); assyMP.assembleComplex(3,resM,resP); Util::printRes(STDOUT,"Accelerations assyRI",assyRI) Util::printRes(STDOUT,"Accelerations assyMP",assyMP)
Finally, FeResPost allow to perform operations on Results that have Complex number arguments. For example, a Result object may be multiplied by a Complex number:
require "complex" Z=Complex.new(3.0,2.0) multRI=resRI.clone multRI*=Z Util::printRes(STDOUT,"Accelerations multRI",multRI) multMP=resMP.clone multMP*=Z Util::printRes(STDOUT,"Accelerations multMP",multMP)
The example “printXdbLcScResSizes.rb” illustrates the extraction of Results from an XDB attachment. The advantage of this method for accessing Results, is that they must no be a priori loaded into a NastranDb object. The attachment is done as follows:
xdbFileName="../../MODEL/EXEC_XDB/sol111_ri_xyz.xdb" db.attachXdb(xdbFileName)
One then selects the load case, the list of sub-cases, and the Result types for the extraction:
lcName="SINUS_X" scNames=[] scNames << "Output 13 (f = 62.0000)" scNames << "Output 14 (f = 63.0000)" scNames << "Output 15 (f = 64.0000)" scNames << "Output 16 (f = 65.0000)" scNames << "Output 17 (f = 66.0000)" scNames << "Output 18 (f = 67.0000)" resNames=[] resNames << "Accelerations, Rotational (RI)" resNames << "Accelerations, Translational (RI)" resNames << "Displacements, Rotational (RI)" resNames << "Displacements, Translational (RI)"
The extraction is then done with a call like this one:
h=db.getAttachmentResults(xdbFileName,lcName,scNames,resNames,"Nodes",grp)
Finally, the Results that have been returned in h (a Hash object) can be retrieved as follows:
h.each do |id,res|
lcName=id[0]
scName=id[1]
resName=id[2]
size=res.Size
STDOUT.printf("%s - %s - %s : %d\n",lcName,scName,resName,size)
end
This section illustrates the manipulation of XDB attachments. All the examples are to be found in directory “RUBY/EX19”. The different examples are in increasing order of difficulty.
In order to reduce the size of extracted Results, the extractions are done on the nodes of a small Group in all the examples below. Note however that other extractions could have been done. Also, if the two last parameters of the extraction functions are omitted, all the Result values are returned by the extraction methods.
In the example “attachedXdbLcInfos.rb”, one shows how content information can be extracted from an attached XDB file. The XDB file must first be attached to the DataBase:
xdbFileName="../../MODEL/EXEC_XDB/sol111_ri_xyz.xdb" db.attachXdb(xdbFileName)
Then, the information is extracted and printed exactly as in one of the examples of section IV.2.4.6:
infos=db.getAttachmentLcInfos(xdbFileName)
infos.each do |tab|
STDOUT.printf("%-20s %-25s %-6d %-6d %-15g %-15g\n",
tab[0],tab[1],tab[3],tab[4],tab[5],tab[6])
end
It is also possible to extract other information like the list of Result names, sub-case names or load cases names. One shows below how the list of result names can be printed:
resNames=db.getAttachmentResNames(xdbFileName)
resNames.each do |resName|
STDOUT.printf("%-20s\n",resName)
end
The example “attachedXdbResults.rb” shows how Results can be extracted from an XDB attachment. As in the previous example, the file is first attached. Then, one decides which result types and for which load case Results are extracted:
lcName="SINUS_Z" resName="Accelerations, Translational (RI)"
Remember than only one load case name can be specified. However, an Array of result names can be provided. In this case, one decides to extract only one result type: “Accelerations, Translational (RI)”. On the other hand, an Array of sub-cases can be specified for the extraction of Results. In this case, the Array is first obtained by calling the “getAttachmentScNames” method:
scNames=db.getAttachmentScNames(xdbFileName)
Then, the Results are extracted as follows:
results=db.getAttachmentResults(xdbFileName,lcName,scNames,resName, "Nodes",grp)
The results are returned in a Hash object that contains pairs of Result keys, and the corresponding Results. The Results can be printed as follows:
results.each do |key,res| Util::printRes(STDOUT,key[1]+" ==> "+key[2],res) end
Note that at the beginning of the script, the buffer total maximum capacity is set to 1Mb as follows:
NastranDb::setStorageBufferMaxCapacity(1.0)
Another example of Results extraction from an XDB attachment is presented in file “attachedXdbExtract.rb”. There several Result types are extracted for a single load case and a single sub-case:
lcName="LAUNCH_ONE_MS2_Y"
scName="Statics"
resNames=[]
resNames << "Shell Forces"
resNames << "Shell Moments"
resNames << "Strain Tensor"
resNames << "Curvature Tensor"
location="ElemCenters"
grp=db.getGroupCopy("pan\_MZ")
layers="NONE"
results=db.getAttachmentResults(xdbFileName,lcName,scName,resNames,
location,grp,layers)
Four Result types have been selected. The list of layers is set to “NONE” to avoid the extraction of Strains on each ply of each element. (One is interested only in the laminate average Strain.)
Results can then be accessed, individually by extracting the elements of the Hash object returned by the “getAttachmentResults” method. For example:
key=[lcName,scName,"Shell Moments"] shMoments=results[key] key=[lcName,scName,"Shell Forces"] shForces=results[key] key=[lcName,scName,"Strain Tensor"] shAvrgStrains=results[key] key=[lcName,scName,"Curvature Tensor"] shCurvatures=results[key]
In order to save time and simplify the programming of post-processing, it is also possible to extract linear combinations of Results. This is presented in example “attachedXdbCombili.rb”.
The linear combination is defined as an Array defining the factors and elementary load cases to consider:
scName="Statics" resName="Displacements, Translational" lcNames=["LAUNCH_ONE_MS2_X","LAUNCH_ONE_MS2_Y","LAUNCH_ONE_MS2_Z"] factors=[100.0, 50.0, 20.0] ... combili=[] (0..2).each do |i| combili << [factors[i], xdbFileName, lcNames[i]] end
Then, the linearly combine Results are extracted as follows:
lcName="CombiLC" results=db.getAttachmentResultsCombili(lcName,combili,scName,resName, "Nodes",grp)
Note that in this case, one single Result object is returned in the “results” Hash object. For example, in this case, one could have provided an Array of Result names instead of the “resName” String argument.
In example “attachedXdbDynamCombili.rb” the same operation is performed for dynamic Results, and an Array of String is provided as list of sub-cases argument. This illustrates the use of “getAttachmentResultsCombili” method returning several Results.
Example “EX19/attachedXdbRandom.rb” illustrates the use of method “calcRandomResponse” in “Post” Module. One calculates the RMS equivalent for a random response.
The calculation is done using the XDB file corresponding to a SOL111 Nastran analysis. The RMS values for accelerations are calculated. The example defines two functions:
Function “psdFunction” calculates the PSD excitation as a function of the frequency. In this case, as the excitation corresponds to a unit acceleration, the units for PSD are . Function “psdFunction” is called by “computeRms” function.
“computeRms” function calculates and returns the RMS value of a result extracted from PSD. The function has 8 arguments:
“db”: a NastranDb object containing the model and XDB attachment from which results are read.
“xdbFileName” is the name of XDB attachment.
“lcName” is the name of the load case for which the results are extracted.
“resName” is the name of the Result to extract from the XDB file.
“maxNbrFreqsPerSlice” is an integer corresponding to the maximum number of Results to be manipulated simultaneously. (One cuts the integration in several “slices” to avoid memory exhaustion when extracting the results.)
“integType” is a String corresponding to the same parameter in “calcRandomResponse” method. Possible values are “LogLog” or “LinLin”.
“method”is a String corresponding to XDB extraction method on Group. This parameter corresponds to the “method” argument of the “getAttachmentNbrResults” method in “NastranDb” class.
“grp” is the Group on which the Results are extracted. This parameter corresponds to the “grp” argument of the “getAttachmentNbrResults” method in “NastranDb””
The first part of “computeRms” function identifies the subcase names in XDB file, for the selected load case, recovers the corresponding frequencies, and sorts the sub-case names by order of increasing frequency:
infos=db.getAttachmentLcInfos(xdbFileName)
h={}
infos.each do |tab|
if tab[0]==lcName then
f=tab[5]
scName=tab[1]
h[f]=scName
end
end
allFreqs=h.keys.sort
totalNbrFreqs=allFreqs.size
Then, the integration is calculated by slices. The “addRes” output of a call to “calcRandomResponse” is used as argument for the next call to the same method. This “addRes” corresponds to the last PSD integration Result object:
idMin=idMax=0 addRes=nil res=nil while idMax<totalNbrFreqs idMin=idMax idMax=[idMin+maxNbrFreqsPerSlice-1,totalNbrFreqs].min freqs=allFreqs[idMin..idMax] scNames=[] psdInput=[] freqs.each do |f| scName=h[f] scNames << scName psdInput << psdFunction(f) end results=db.getAttachmentResults(xdbFileName,lcName,scNames, resName,method,grp) sortedResults=[] scNames.each do |scName| sortedResults << results[[lcName,scName,resName]] end ret=Post.calcRandomResponse(false,false,sortedResults,freqs, psdInput,integType,addRes) addRes=ret[1] res=ret[2] end
One presents in this section a few examples that provide at the same time, tools that can be useful in many projects.
When sizing a satellite’s structure, one is often asked to define load cases corresponding to quasi-static accelerations on sub-parts of the structure. For example, at system level, dynamic analyses have shown that the upper part of the structure may be submitted to more severe accelerations than the rest of the satellite.
Unfortunately, Nastran does not allow the definition of quasi-static accelerations on sub-parts of the structure. The “GRAV” card, only allows the definition of accelerations globally on the whole structure.
It is possible to solve the problem in two steps:
One calculates with Nastran three elementary load cases corresponding to unit accelerations of 1 applied on the entire structure oriented on the three structural axes respectively. The definition of these loads is done with Nastran “GRAV” cards.
Then one recovers the finite element Results of the Nastran “op2” file, and after performing some operations on the Results, one performs an appropriate printing of the Results to produce “FORCE” Nastran Bulk cards. Two different results can be used to perform this operation: the applied loads provided by “OLOAD” output, or the applied loads obtained from “GPFORCE” output.
This method is equivalent to the production of a force field.
In this examples, one defines several functions. Therefore, a module “Grav” has also be created, and all functions are placed in the module. A first utility function is used to add to a DataBase a new Group created by performing a union of elementary Groups:
def Grav.AddNewGroupsByUnions(db,totalGroupName,elemGroupNames) totalGroup=Group.new() for i in 0...elemGroupNames.size elemGroup=db.getGroupCopy(elemGroupNames[i]) totalGroup+=elemGroup end totalGroup.Name=totalGroupName db.addGroupCopy(totalGroup) end
The first argument is the DataBase from which the elementary Groups are Retrieved and to which the new Group is created. The second argument is a String object the value of which is the new Group name. The last argument is an Array of Strings containing the names of the elementary Groups.
Another function is devoted to the printing of the “FORCE” Nastran Bulk Data Cards in a file. The function is defined as follows:
def Grav.writeForce(fileName,lcId,coordSysId,forces) print "creating file " puts fileName table=forces.getData() cards=[] for oneRes in table values=[] values << lcId; values << oneRes[1] values << coordSysId x=oneRes[5] y=oneRes[6] z=oneRes[7] norm=Math.sqrt(x*x+y*y+z*z) if (norm>1.0e-10) then values << norm values << x/norm values << y/norm values << z/norm end cards << values end NastranDb.writeNastranCards(fileName,"w","left","short","FORCE",cards); end
This function has four arguments:
A String corresponding to the name of the file in which the cards are printed.
An integer corresponding to the load case identifier.
An integer corresponding to the coordinate system in which the components of the “FORCE” vectors are given.
A Result object containing the nodal forces. The Result must be vectorial and defined at nodes. Also the forces should be expressed in the coordinate system identified by the third argument.
The function works as follows:
First, one opens the output file for writing.
One recovers the data stored in the Result argument.
Then, for each vector, one saves it into the “cards” array, but only if the norm of the vector is larger than a specified value (not equal to zero).
At the end, the printing is done by a call to “writeNastranCards” method.
This version of the method is proposed in “RUBY/EX06/makeGravForces.rb”file.
Another version of the function, provided in “RUBY/EX06/makeGravForcesB.rb” reads as follows:
def Grav.writeForce(fileName,lcId,coordSysId,forces) print "creating file " puts fileName table=forces.getData() cards=[] for oneRes in table values=[] values << "FORCE" values << lcId; values << oneRes[1] values << coordSysId x=oneRes[5] y=oneRes[6] z=oneRes[7] norm=Math.sqrt(x*x+y*y+z*z) if (norm>1.0e-10) then values << norm values << x/norm values << y/norm values << z/norm end cards << values end NastranDb.writeNastranCards(fileName,"w","left","short",cards); end
Remark that one uses the “5 arguments” version of “writeNastranCards” method. (The “cardName” argument is omitted.) On the other hand, each “values” Array has one additional element. The first element of the Array is the “FORCE” card name.
The function “Grav.genAllGravFields” is the function that performs the extraction of force fields from the Results stored in the DataBase:
def Grav.genAllGravFields(db,data)
nbr=data.size
for i in 0...data.size
groupName=data[i][0]
extName=data[i][1]
baseLID=data[i][2]
csId=1001
target=db.getGroupCopy(groupName)
forces1=db.getResultCopy("LAUNCH_ONE_MS2_X","Statics",\
"Applied Loads, Forces","Nodes",target,[])
forces1.modifyRefCoordSys(db,csId)
forces2=db.getResultCopy("LAUNCH_ONE_MS2_Y","Statics",\
"Applied Loads, Forces","Nodes",target,[])
forces2.modifyRefCoordSys(db,csId)
forces3=db.getResultCopy("LAUNCH_ONE_MS2_Z","Statics",\
"Applied Loads, Forces","Nodes",target,[])
forces3.modifyRefCoordSys(db,csId)
Grav.writeForce("force1_"+extName+".bdf",baseLID+1,csId,forces1)
Grav.writeForce("force2_"+extName+".bdf",baseLID+2,csId,forces2)
Grav.writeForce("force3_"+extName+".bdf",baseLID+3,csId,forces3)
GC.start()
end
end
This function receives two arguments:
The DataBase from which the Results are extracted.
An Array of Arrays containing the information necessary for the production of the different force fields. Each element Array contains three elements:
A String object containing the name of the Group on which the Result forces are retrieved.
A String containing the name of the extension to be added to the output file name.
An integer corresponding to the base of the load identifier by which the force field shall be referred in the bulk data file. (Actually, three force fields are produced for each Group in the directions X, Y and Z respectively. The corresponding identifiers are produced by adding 1, 2 or 3 respectively to the base identifier of the load.
The function performs a loop on all the elements of the “data” Array argument. For each element
The function recovers the data stored in the current element (name of the Group, extension to be added to the output file name, and base of the load identifier).
The coordinate system on which the force components are expressed are always 1001. (This means that the function is not general and depends on the existence of a corresponding coordinates system in the DataBase.)
One recovers a Copy of the Group from the DataBase and stores it into “target”.
One recovers from the DataBase the forces corresponding to the three load cases
“LAUNCH_ONE_MS2_X”,
“LAUNCH_ONE_MS2_Y” and “LAUNCH_ONE_MS2_Z”. Here again, this is done
assuming that the corresponding Results have been loaded into the DataBase before.
Moreover, these load cases are assumed to correspond to unit accelerations in direction X,
Y and Z respectively. The Results are stored in variables “force1”, “force2” and “force3”
respectively.
For each force field, one modifies the reference coordinate system and sets it to 1001.
Then the corresponding Results are printed by calling function “Grav.writeForce”.
Finally The “main” function looks like this:
def Grav.main()
# Creation of the dataBase :
db=NastranDb.new()
db.Name="tmpDB"
db.readBdf("../../MODEL/MAINS/unit_xyz.bdf")
db.readGroupsFromPatranSession("../../MODEL/PATRAN/groups.ses")
Grav.AddNewGroupsByUnions(db,"upper_set",\
["pan_SUP", "struts_ALL", "fittings_ALL"])
# Reading of results :
db.readOp2("../../MODEL/EXEC_OP2/unit_xyz.op2","Results")
# Production of force fields :
data=Array.new()
data.push(["pan_MX", "PAN_MX", 611000])
data.push(["pan_MY", "PAN_MY", 612000])
data.push(["pan_MZ", "PAN_MZ", 613000])
data.push(["pan_PX", "PAN_PX", 614000])
data.push(["pan_PY", "PAN_PY", 615000])
data.push(["pan_PZ", "PAN_PZ", 616000])
data.push(["upper_set", "UPPER", 617000])
Grav.genAllGravFields(db,data)
end
It works as follows:
First the DataBase is initialized by reading the model and the Groups.
A new Group, produced by union of several Groups is added to the DataBase.
Results are read into the DataBase by calling “readOp2” method.
The data are produced by filling the “data” Array.
Finally, one calls function “Grav.genAllGravFields” with the appropriate arguments.
The program is executed by a call to main function:
Grav.main()
Note that some of the output files produced by this example are used in the definition of loads for Nastran calculations in Chapter IV.1.
These examples are provided in files "RUBY/EX06/makeGravForces.rb" and "RUBY/EX06/makeGravForcesB.rb".
This example is similar to the previous one, but instead of generating “FORCE” fields, one generates temperature fields with “TEMP” Nastran cards. Also, the example differs by the fact that no Results are read from an “op2” file.
One writes two functions devoted to the printing of “TEMP” cards in a Bulk Data File. The first function writes a constant temperature field on a Group:
def Therm.writeConstTempCards(fileName,lcId,target,constT)
print "creating file "
puts fileName
nodes = target.getEntitiesByType("Node")
index = 0
cards=[]
while index < nodes.size
if (nodes.size-index>=3) then
values = []
values << lcId
for i in 0..2
values << nodes[index]
values << constT
index+=1
end
else
values = []
values << lcId
for i in 0...(nodes.size-index)
values << nodes[index]
values << constT
index+=1
end
end
cards << values
end
NastranDb.writeNastranCards(fileName,"w+","left","short",
"TEMP",cards);
end
The principle of the function is that one recovers the list of nodes contained in the Group. Then for each node, one writes a “TEMP” entry. The second printing function prints a temperature field corresponding to a scalar Result object:
def Therm.writeFieldTempCards(fileName,lcId,tempField) print "creating file " puts fileName tempData = tempField.getData index = 0 size = tempData.size cards=[] while index < size if (size-index>=3) then values = [] values << lcId for i in 0..2 values << tempData[index][1] values << tempData[index][5] index+=1 end else values = [] values << lcId for i in 0...(size-index) values << tempData[index][1] values << tempData[index][5] index+=1 end end cards << values end NastranDb.writeNastranCards(fileName,"w+","left","short", "TEMP",cards); end
The principle of the function is very similar to the principle of function “FORCE” field printing function described in section IV.2.5.1.
The main function begins with an initialization of the DataBase:
db=NastranDb.new()
db.Name="tmpDB"
db.readBdf("../../MODEL/MAINS/orbit_unit_xyz.bdf")
db.readGroupsFromPatranSession("../../MODEL/PATRAN/groups.ses")
Then one defines constant temperature fields on parts of the structure. One defines four cases obtained by a combination of cold or hot temperatures, and application to two Groups. The second Group is build by assembling the lateral panels. This part of the main functions looks like:
# Generation of temperature fields on panel +Z :
tmpGrp = db.getGroupCopy("pan_PZ")
Therm.writeConstTempCards("temp_P120_PAN_PZ.bdf",621001,tmpGrp, 120.0)
Therm.writeConstTempCards("temp_M100_PAN_PZ.bdf",621001,tmpGrp,-100.0)
# Generation of temperature fields on lateral panels :
tmpGrp = db.getGroupCopy("pan_PX")
tmpGrp += db.getGroupCopy("pan_PY")
tmpGrp += db.getGroupCopy("pan_MX")
tmpGrp += db.getGroupCopy("pan_MY")
Therm.writeConstTempCards("temp_P120_PAN_LAT.bdf",622001,tmpGrp, 120.0)
Therm.writeConstTempCards("temp_M100_PAN_LAT.bdf",622002,tmpGrp,-100.0)
One also defines temperature fields by production of a corresponding Result object. In this case, the Result is build from the coordinates:
# Generation of a temperature gradient field :
tmpGrp = Group.new
tmpGrp.setEntities("Node 1:99999")
tmpGrp.matchWithDbEntities(db)
db.generateCoordResults
coords=db.getResultCopy("","","Coordinates","NodesOnly",tmpGrp,[])
coords.modifyPositionRefCoordSys(db,1001)
tGradX=coords*[100.0, 0.0, 0.0]
Therm.writeFieldTempCards("temp_GRAD_X.bdf",623001,tGradX)
tGradY=coords*[ 0.0, 100.0, 0.0]
Therm.writeFieldTempCards("temp_GRAD_Y.bdf",623002,tGradY)
tGradZ=coords*[ 0.0, 0.0, 100.0]
Therm.writeFieldTempCards("temp_GRAD_Z.bdf",623003,tGradZ)
Note that the previous ruby lines illustrate the use of several capabilities of FeResPost:
The Group of nodes “tmpGrp” is build by defining a range of nodes. After this operation, the Groups contains the list of nodes numbered 1 to 99999. Most of these nodes do not exist in the finite element model. To Ensure that they exist, one matches the Group against the DataBase.
temperature fields are build from coordinate field. This means that the coordinate Results are created in the DataBase by a call to “generateCoordResults”. Then they are extracted on the nodes of the Group.
Note that the temperature fields printed in BDF files are used in the definition of loads for Nastran calculations in Chapter IV.1.
The example is provided in file "RUBY/EX07/makeTempFields.rb".
One explains here how the resulting global force and moment can be calculated from distributed force and moments. This example illustrates the use of method “calcResultingFM” in class “Result”.
The ruby function that performs the calculation of the total force and moments looks like follows:
def calcOneGlobFM(db,lcName,scName,elemGrp,nodeGrp,locCS,coords) # Target Group : targetGrp = Group.new() tmpNodeGrp=db.getNodesAssociatedToElements(elemGrp) targetGrp = tmpNodeGrp * nodeGrp tmpElemGrp=db.getElementsAssociatedToNodes(targetGrp) targetGrp += tmpElemGrp * elemGrp # Inspecting and reading Results : tpNameF = "Grid Point Forces, Internal Forces" tpNameM = "Grid Point Forces, Internal Moments" tmpF = db.getResultCopy(lcName,scName,tpNameF,"ElemNodes",targetGrp,[]) tmpM = db.getResultCopy(lcName,scName,tpNameM,"ElemNodes",targetGrp,[]) resFM = Result.calcResultingFM(db,tmpF,tmpM,locCS,coords) return resFM end
The arguments of the function are:
“db”, the DataBase given as argument to “calcResultingFM”.
“lcName”, a String containing the name of the load case for which the results are retrieved.
“scName”, a String containing the name of the sub-case for which the results are retrieved.
“elemGrp”, a Group containing the elements from which one recovers the local forces and moments.
“nodeGrp”, a Group containing the nodes on which the forces will be recovered.
“locCS”, the coordinate system in which results are recovered. Its value can be of integer or CoordSys type.
“coords”, an Array of three Real values containing the coordinates of the recovery point expressed in the coordinate system.
The function builds a Group called “targetGrp” containing the list of elements and nodes on which Grid Point Forces and Moments are recovered. To reduce the computation cost, the targetGrp object contains only the elements and nodes on which the results are recovered. One this Group is defined, one recovers the corresponding Force and Moment fields, and an appropriate call to “Result.calcResultingFM” calculates the resulting total force and moment which are returned by the function.
The main part of the example consists in building the DataBase, loading the Results and performing the calculations for any combination of three load cases and six interfaces. The definition of load cases and interfaces are done as follows:
lcNames = ["LAUNCH_ONE_MS2_X", "LAUNCH_ONE_MS2_Y", "LAUNCH_ONE_MS2_Z"] scName = "Statics" interfaces=Array.new() interfaces << ["pan_PZ", "fitting_PXMYMZ",1001,[ 0.440000,-0.440, 0.6445]] interfaces << ["pan_PZ", "fitting_MXMZ", 1001,[-0.426667, 0.000, 0.6445]] interfaces << ["pan_SUP","fitting_MXMYPZ",1002,[ 0.310835,-120.0, 1.4000]] interfaces << ["pan_SUP","fitting_PXPZ", 1002,[ 0.310835, 0.0, 1.4000]] interfaces << ["pan_SUP","fitting_MXPYPZ",1002,[ 0.310835, 120.0, 1.4000]] interfaces << ["pan_PZ", "fitting_PXPYMZ",1001,[ 0.440000, 0.440, 0.6445]]
Then the loops on data are performed, with the calls to “calcOneGlobFM”, and the results are printed:
for lcName in lcNames printf "\n %s :\n\n",lcName for interf in interfaces elemGrp = db.getGroupCopy(interf[0]) nodeGrp = db.getGroupCopy(interf[1]) cs=interf[2] coords=interf[3] fm = calcOneGlobFM(db,lcName,scName,elemGrp,nodeGrp,cs,coords) f=fm[0] m=fm[1] printf "%20s%20s%10d%10.3f%10.3f%10.3f%10.3f%10.3f%10.3f\n",\ elemGrp.Name,nodeGrp.Name,cs,\ f[0],f[1],f[2],m[0],m[1],m[2] end end printf "\n"
Typically, the calculation of global force and moment for a given interface can be used to estimate loads to be used to calculate a detailed model (of a metallic fitting, for example). It can also be used for post-processing (for example to calculate margins of safety for a global sliding of an interface).
The example is provided in file "RUBY/EX10/makeTempFields.rb".
This example illustrates the creation of a Gmsh file for later visualization with Gmsh. The part of the data file specific to the “writeGmsh” function call is as follows:
# Group creation :
meshGrp=db.getGroupAllFEM
targetGrp = db.getGroupCopy("pan_PZ_Al_2024")
targetGrp2 = db.getGroupCopy("pan_PZ")
# Stress data in skins :
stress = db.getResultCopy("TEMP_GRAD_X","Statics",\
"Stress Tensor","ElemCenters",targetGrp,[])
stress2 = db.getResultCopy("TEMP_GRAD_X","Statics",\
"Stress Tensor","ElemCorners",targetGrp,[])
displ = db.getResultCopy("TEMP_GRAD_X","Statics",\
"Displacements, Translational","Nodes",targetGrp2,[])
norm = displ.deriveVectorToOneScal("abs")
# Stress data in honeycomb :
targetGrp =tmpGroup_Honey_72
honeyStress=db.getResultCopy("TEMP_GRAD_X","Statics",\
"Stress Tensor","ElemCenters",targetGrp,[])
# Gmsh output :
db.writeGmshMesh("brol.msh",0,meshGrp,false)
db.writeGmsh("brol.gmsh",0,[[stress,"stress","ElemCenters"],\
[stress2,"stress2","ElemCorners"],\
[honeyStress,"honeyStress","ElemCenterPoints"],\
[displ,"displ","Nodes"],\
[norm,"norm","Nodes"]],\
[[db.getGroupCopy("pan_PZ"),"mesh pan_PZ"],\
[db.getGroupCopy("pan_MZ"),"mesh pan_MZ"],\
[db.getGroupCopy("pan_PX"),"mesh pan_PX"]],\
[[meshGrp,"skel sat"]])
Actually, only the last function call is new. The example is provided in file "RUBY/EX11/writeGmsh.rb".
“Result” and “Group” objects can be saved into SQL BLOBs for storing or manipulation in SQL databases. This feature has been introduced to allow the management of persistence of intermediate results calculated with FeResPost.
One proposes here a small example illustrating this feature. The example deals with Nastran dynamic analysis Results that are store into an SQLite database. This type of operation may be handy, as the access to dynamic analysis results from an XDB file may sometimes be very unpractical. In particular, the insertion table is organized in such a way that Results can be accessed separately by subcases.
This example is based on SQLite database system but the adaptation to other SQL database systems should not be a problem. To run the example you must first install the “sqlite3” ruby gem on your computer.
To use SQLite, one first requires the corresponding ruby gem:
require "rubygems" require "sqlite3"
Then, the database can be created:
fName="brol.fdb" if (File::exists?(fName)) sqldb = SQLite3::Database.open( fName ) else sqldb = SQLite3::Database.new( fName ) sqldb.execute <<SQL PRAGMA auto_vacuum = FULL SQL end
In this case only one SQL table is created in the database. The columns correspond to several data associated with each individual Results, and the BLOB corresponding to the Result itself:
sqldb.execute <<SQL CREATE TABLE IF NOT EXISTS dynam_results_1 ( lcName TEXT, scName TEXT, resName TEXT, tensorOrder INTEGER, intId1 INTEGER, intId2 INTEGER, realId1 REAL, realId2 REAL, size INTEGER, result BLOB, PRIMARY KEY(lcName,scName,resName) ); SQL
Finally, one loops on xdb attachment Results. For each load case and Result name, one extracts the Results corresponding to each subcase, and inserts it into the database:
db.attachXdb(xdbFileName) lcNames=db.getAttachmentLcNames(xdbFileName) scNames=db.getAttachmentScNames(xdbFileName) resNames=db.getAttachmentResNames(xdbFileName) lcNames.each do |lcName| resNames.each do |resName| results=db.getAttachmentResults(xdbFileName,lcName,scNames,resName) if (results) then results.each do |key,res| puts key sqldb.execute( "insert or replace into dynam_results_1 values (?,?,?,?,?,?,?,?,?,?)", lcName,key[1],resName,res.TensorOrder, res.getIntId(0),res.getIntId(1), res.getRealId(0),res.getRealId(1),res.Size, SQLite3::Blob.new(res.toBlob())) end else puts "NO FOR" + lcName + resName end end
The example is provided in file "RUBY/EX20/rehashDynamicResults.rb"
This example, uses the database created in the example of section IV.2.6.1 and retrieves Results or deletes some of the data. An example of statements that allow to retrieve Results is given below:
sqldb.query("select * from dynam_results_1 where lcName = ? and realId1 = ?",
["SINUS_X",97.0] ).each do |tab|
puts tab[0],tab[1],tab[2],tab[8]
res=Post.convertBlob(tab[9])
puts res.Size()
end
Items can be deleted from database by statements of this type:
sqldb.execute("delete from dynam_results_1 where resName = ?",
"Strain Tensor (RI)" )
sqldb.execute("delete from dynam_results_1 where resName = ?",
"Applied Loads, Forces (RI)" )
sqldb.execute("delete from dynam_results_1 where resName = ?",
"Applied Loads, Moments (RI)" )
sqldb.execute("delete from dynam_results_1 where resName = ?",
"Accelerations, Rotational (RI)" )
sqldb.execute("delete from dynam_results_1 where resName = ?",
"Velocities, Rotational (RI)" )
sqldb.execute("delete from dynam_results_1 where resName = ?",
"Displacements, Rotational (RI)" )
sqldb.execute("delete from dynam_results_1 where realId1 < ?",
90.0 )
The example is provided in file "RUBY/EX20/deleteSomeResults.rb"
One provides here an example for the reading of optimization results. The first steps of the example consists in the creation of a NastranDb object, and the attachment of an XDB file:
db=NastranDb.new()
db.Name="tmpDB"
#~ db.readBdf("../../MODEL/EXEC_XDB/sol200_a.bdf")
xdbFileName="../../MODEL/EXEC_XDB/sol200_a.xdb"
#~ xdbFileName="../../MODEL/EXEC_XDB/sol200_b.xdb"
db.attachXdb(xdbFileName)
Remark, that the reading of the Nastran finite element model from a BDF file is not necessary to access optimization results.
In the Nastran examples, one provides two optimization runs:
“sol200_a.bdf” for an optimization with design variables.
“sol200_b.bdf” for a topometric optimization.
The two runs lead to similar kinds of outputs, including the history of design variables. Only, the topometric optimization generates automatically design variables (for example, one variable per element). Then, the numbering of design variables kind by awkward.
The printing of design variables history is done with the following ruby instructions:
x=db.getAttachmentDesVarHistory(xdbFileName,nil,nil)
STDOUT.printf("%14s%14s%14s\n","STEP","DVID","VALUE")
x.each do |tab|
STDOUT.printf("%14d%14d%14f\n",tab[0],tab[1],tab[2])
end
In this case, one prints the history of all design variables, and for all steps. (“nil” values are passed for corresponding arguments of the “getAttachmentDesVarHistory” method.) If you do the same with “sol200_b.xdb”, file, you will obtain a very long output as the number of design variables can be very large for topometric optimization.
The definition of constraints is printed as follows:
x=db.getAttachmentConstrDefinitions(xdbFileName)
STDOUT.printf("%8s%8s%8s%8s%8s%14s\n","IDCID","DCID","IRID","TYPE","LUFLAG","BOUND")
x.each do |tab|
str=""
if tab[4]==1 then
str=">"
elsif tab[4]==2 then
str="<"
end
STDOUT.printf("%8d%8d%8d%8d%8s%14f\n",tab[0],tab[1],tab[2],tab[3],str,tab[5])
end
And the corresponding histories are obtained as follows:
x=db.getAttachmentConstrHistory(xdbFileName)
STDOUT.printf("%8s%8s%14s\n","STEP","IDCID","VALUE")
x.each do |tab|
STDOUT.printf("%8d%8d%14f\n",tab[0],tab[1],tab[2])
end
Here, the history is printed for all optimization steps, as the corresponding parameter is not provided.
And similarly, the objective history is printed as follows:
x=db.getAttachmentObjectiveHistory(xdbFileName)
STDOUT.printf("%8s%14s%8s%14s\n","STEP","OBJ.","IRID","Cst. VALUE")
x.each do |tab|
STDOUT.printf("%8d%14f%8d%14f\n",tab[0],tab[1],tab[2],tab[3])
end
You can remark that when a topometric optimization is calculated by Nastran as a design variable optimization. (Nastran defines automatically one design variable per element.)
The example is provided in file "RUBY/EX21/printSol200Infos.rb".
In directory “RUBY/EX22”, one presents several examples with Ruby extension that illustrates the raw access to XDB files. (The corresponding examples for COM component and .NET assembly are provided in directories “COMEX/EX13” and “NETEX/EX22”.)
In file “dictPrint.rb” one defines two methods that print the list of dictionnary keys, and/or the entire dictionnary. These methods are:
“printDictKeys” prints the list of dictionnary keys.
“printDictionnary” prints the dictionnary. (This can be useful if one does not know the field size for a given table.)
(These two methods are called in the different examples.)
The example is provided in “RUBY/EX22/recoverCSTM.rb”. The interesting part of the example is the use of the iterator:
db.iter_xdbRaw(xdbFileName,["CSTM",0],"iiffffffffffffifffffffff").each do |tab|
STDOUT.printf("Coordinate system ID: %d\n",tab[0])
STDOUT.printf("Coordinate system type: %d\n",tab[1])
STDOUT.printf("Coordinate system origin (wrt 0): %14g %14g %14g\n",
tab[2],tab[3],tab[4])
STDOUT.printf("Coordinate system V1 (wrt 0) : %14g %14g %14g\n",
tab[5],tab[6],tab[7])
STDOUT.printf("Coordinate system V2 (wrt 0) : %14g %14g %14g\n",
tab[8],tab[9],tab[10])
STDOUT.printf("Coordinate system V3 (wrt 0) : %14g %14g %14g\n",
tab[11],tab[12],tab[13])
end
Note that the CSTM table correspond to a FEM modeling table and not to a result table. This shows that the raw access to XDB file can be used to access modeling information.
Generally, maximum one table per type is defined in XDB file, if the table corresponds to modeling information. However, this is sometimes different. For example FEM modeling table may correspond to an output of optimization run.
One also presents an example in which the ‘each_xdbBinRaw” iterator is used with “binDataToValues” singleton method to interpret the content of XDB file. The example is provided in “RUBY/EX22/recoverBINRAW.rb” script and its main part looks as follows:
wdSize=db.getAttachmentWordsSize(xdbFileName)
bSwap=db.getAttachmentSwapEndianness(xdbFileName)
policy=0
if (bSwap) then
policy=1
end
bAutoSwap=true
cards=[]
db.each_xdbBinRaw(xdbFileName,["CQD4",0],bAutoSwap) do |str|
arri=NastranDb.binDataToValues(str,wdSize,"iiiiiiii iiiii".delete(’ ’),policy)
arrf=NastranDb.binDataToValues(str,wdSize,"iiiiiiff fiiii".delete(’ ’),policy)
puts arri.size()
card=["CQUAD4"]+arri
#~ puts arri,arrf
cards << card
end
NastranDb.writeNastranCards("output.bdf","w","right","wide",cards)
Note that we output the read values into a kind of BDF file, but you will notice that the cards do not really match the corresponding CQUAD4 card definition. you may notice that we also use the getAttachmentWordsSize and getAttachmentSwapEndianness methods to determine the endianness policy for binary data translation.
We give here an example, in which CBAR element forces are read from the XDB file. This is done to illustrate the extraction of element results. Otherwise, there is no practical use to this example, as the corresponding extractions can be done by the “usual” XDB result extraction methods. The example is provided in file “RUBY/EX22/recoverFBAR.rb”.
One first attempts to access the definition of load cases:
db.each_xdbRaw(xdbFileName,["SUBCASES",0],"iiiiiiii") do |tab|
puts tab
end
str="i"
(0..95).each do |i|
str+="s"
end
db.each_xdbRaw(xdbFileName,["SUBCTITL",0],str) do |tab|
STDOUT.printf("%d\n",tab[0])
(0..2).each do |j|
str=""
(1..32).each do |i|
str+=tab[32*j+i]
end
str.strip!
STDOUT.printf("%s\n",str)
end
end
The integers extracted from “SUBCASES” table correspond to sub-case integer ID, the corresponding load ID, the SPC ID... The access to “SUBCTITL” shows how strings must be concatenated when they correspond to several words.
The reading of CBAR forces is done as follows:
modulo=-1;
db.each_xdbRaw(xdbFileName,["FBARR",2],"iiiiiiiii") do |tab|
if (tab[0]==0) then
modulo=tab[1]
end
break;
end
db.each_xdbRaw(xdbFileName,["FBARR",2],"iffffffff") do |tab|
accessType=12
if (tab[0]>0) then
elemIntId=tab[0]/modulo
elemExtId=db.getAttachmentElementExtId(xdbFileName,accessType,elemIntId)
STDOUT.printf("%30s : %d\n","Element ID",elemExtId)
STDOUT.printf("%30s : %g\n","M bending A 1",tab[1])
STDOUT.printf("%30s : %g\n","M bending A 2",tab[2])
STDOUT.printf("%30s : %g\n","M bending B 1",tab[3])
STDOUT.printf("%30s : %g\n","M bending B 2",tab[4])
STDOUT.printf("%30s : %g\n","F shear 1",tab[5])
STDOUT.printf("%30s : %g\n","F shear 2",tab[6])
STDOUT.printf("%30s : %g\n","F axial",tab[7])
STDOUT.printf("%30s : %g\n\n","M torque",tab[8])
end
end
One must add a few explanations:
The first call to iterator is done to access the first “void” field. This allows to identify an integer “modulo” that is used later to calculate the element internal ID for each field. There is a “break” statements that forces an exit from iterator loop once the modulo has been identified.
Then, one calls the iterator a second time to perform the “real” reading of element results. Note that the string “translation” argument is not the same.
The definition of the translation string has been done by trials and errors. The reading of Nastran documentation may help (for example the structure of OP2 data blocks in Nastran DMAP manual [Rey04]) to understand the output, but there is no detailed description of XDB file content in MSC.Access documentation. This is true for results tables, as well as for FEM description tables.
For the “real” reading, one skips the “modulo” part.
The element access type is set to 12 as one extracts forces on CBAR elements.
The element internal ID is obtained by dividing key by the modulo.
Method “getAttachmentElementExtId” is used to obtain the element external ID (Nastran element ID).
We provide here an example where modeling information is read from the XDB file. The modeling information corresponds to the last output of a topometric optimization. The purpose of the script is to produce a “clean” FEM corresponding to the topometric optimization. The example is given in “RUBY/EX22/recoverTopometricModel.rb”.
The reading of PSHELL cards is done as follows:
pshellCards={}
db.each_xdbRaw(xdbFileName,["PSHELL",49],"iifififfffi") do |tab|
card=[]
card << "PSHELL"
(0...10).each do |i|
if (tab[i].class==Float&&tab[i].nan?) then
card << ""
else
card << tab[i]
end
end
if (tab[10]==0) then
card << ""
else
card << tab[10]
end
pshellCards[tab[0]]=card
end
Remark that:
The XDB file contains in this case 50 “PSHELL” tables because one outputs the results of all optimization steps. One reads only the last “PSHELL” table. (Its index is 49 as the numbering starts with 0.)
Here again, the identification of “real” and “integer” values has been done by trials and errors. (If you print the translated values in an output file, you see easily if you have made an error.)
A similar reading is done in for the CQUAD4 elements.
Also, if you print the PSHELL cards, you will discover the for a topometric optimization, Nastran generates a very large number of PSHELL cards. (One card per element in the group of topometric optimization.) In our example, the numbering of the newly generated cards starts with 1000000.
The CQUAD4 elements that are read refer to the new generated property IDs.
In the rest of the script, one generates renumbered PSHELL cards. Each PSHELL PID will be the same as the element ID of the CQUAD4 that refers to the property. The CQUAD4 elements are modified accordingly. The new Nastran cards are output in “newModel.bdf” file, and a GMSH file corresponding to the modified thicknesses is output:
outputCards=[]
propRemap={}
elemIds=cquad4Cards.keys.sort
elemIds.each do |elemId|
elemCard=cquad4Cards[elemId].clone
propId=elemCard[2]
if propId>1000000 then
elemCard[2]=elemId
propRemap[propId]=elemId
end
outputCards << elemCard[0..7]
end
propIds=pshellCards.keys.sort
res=Result.new
res.TensorOrder=0
res.Format=1
propIds.each do |propId|
propCard=pshellCards[propId].clone
if propRemap.has_key?(propId) then
propCard[1]=propRemap[propId]
res.insert([propCard[1]],["NONE",propCard[3]])
end
outputCards << propCard[0..8]
end
NastranDb::writeNastranCards("newModel.bdf","w","right","short",outputCards)
#~ Util::printRes($stdout,"brol",res)
db.writeGmsh("thicknesses.gmsh",0,[[res,"thickness","ElemCenters"]])
Note that the example could be improved. For example, you could also consider the CTRIA3 elements in the model generation.
In order to calculate laminate load response from the distribution of shell forces and moments, it is sometimes also necessary to know the temperature distribution for each load case.
Example “RUBY/EX22/recoverTEMP.rb” reads the “TEMP” cards from the XDB files and stores them in an SQLite database. More precisely, function “getXdbTemperature”:
Initializes all the nodes to a default temperature for each load case:
grpNodes=db.getGroupAllNodes()
tempFields={}
hTD.each do |tempId,temp|
tempRes=Result.new
tempRes.Name="temperature"
tempRes.Format=1
tempRes.TensorOrder=0
grpNodes.each_node do |nodeId|
tempRes.insert(["NONE",nodeId],["NONE",temp])
end
tempFields[tempId]=tempRes
end
(The “TEMPD” cards are not saved in XDB file, and the default temperature for each load case must be provided by the user. In function “getXdbTemperature” the default temperatures are provided in a Hash that associates the load case integer IDs to real temperatures.)
The “SUBCASES” and “SUBCTITL” tables are also read from the XDB file. These tables allo to associate temperature fields to subcase names. Note that in the method, one uses the ‘TEMP(LOAD)” but not the “TEMP(INIT)”.
The method returns a hash object that associates temperature IDs to corresponding scalar results.
Method “saveResultsInSqlite” is used to save the temperature fields into a SQLite database. The table is called “element_temperatures” and associates integer keys (the Nastran temperature load ID) to BLOB objects corresponding to the temperature fields (FeResPost Result object).
These temperature fields can be used in other post-processing scripts to estimate laminate load response analysis from finite element model results. The SQLite database is here called “sqliteResults.db3”.
An example showing how the temperature fields stored in the SQLite database can be used is presented in section VII.4.4.3
Example “RUBY/EX23/testHDF.rb” illustrates the reading of Nastran HDF file results. First, the library must be loaded:
Post.loadHdf5Library("C:/NewProgs/HDF5/HDF5-1.8.20-win32/bin/hdf5.dll")
Then, the different methods described in section III.1.1.11 are used to access results stored in the HDF file. In the example below, HDF file is attached to the database, the available load case names, subcase name and result names are retrieved, and some of the Results are read into the database.
db.attachHdf(hdfName)
lcNames=db.getHdfAttachmentLcNames(hdfName)
lcName=lcNames[0]
scNames=db.getHdfAttachmentScNames(hdfName,lcName)
scName=scNames[0]
resNames=db.getHdfAttachmentResNames(hdfName,lcName)
hdfResNames=resNames.clone
db.getHdfAttachmentLcInfos(hdfName).each do |info|
os.printf("%s%30s%8d%8d%14f%14f\n",
info[0],info[1],info[3],info[4],info[5],info[6])
end
db.readHdfAttachmentResults(hdfName,lcName,scName,resNames)
Example “RUBY/EX26/hdf_dataset_iteration.rb” illustrates the raw reading of Nastran HDF file content. First, the library must be loaded:
Post.loadHdf5Library("C:/NewProgs/HDF5/HDF5-1.8.20-win32/bin/hdf5.dll")
Then, HDF5 file is attached and different methods are called to obtain information on the content of the file. In particular, one identifies the different Datasets contained in the file, and their characteristics (Compound members, and number of items).
db.attachHdf(h5Path)
dsets=db.getHdfAttachmentDataSets(h5Path)
dsets.each do |dsPath|
members=db.getHdfAttachmentCompoundMemberNames(h5Path,dsPath)
nbrLines=db.getHdfAttachmentDataSetNbrItems(h5Path,dsPath)
printf("%s (%d*%d)\n",dsPath,nbrLines,members.size)
members.each do |str|
printf("%20s\n",str)
end
end
In the end, one interates on content with insractions as
db.each_hdfAttachmentNasSetItem(h5Path,dsets[2],iMin,iMax) do |x|
puts x
$stdout.printf("\n\n")
end
The raw reading of Dataset content in an Array is shown in example “TESTSAT/RUBY/EX26/hdf_dataset_array.rb”.
One discusses in this section the example provided in directory “TESTSAT/RUBY/EX27” and that illustrate the management of Results when model contains superelements. (See section III.1.1.3 for the presentation of the theory.)
All the examples presented here are based on the reading of models in directory
“TESTSAT/OTHER_EXECS/msc_seug_chapter2_Jet" and of associated results in OP2, XDB or
HDF files. The Nastran BDF files have been obtained modifying MSC Nastran example
“doc/seug/chapter2/jet101.dat” in Nastran installation directory. This example is discussed in [Hex22].
Modifications have been done to obtain the OP2, XDB or HDF output files with results associated to
the different superelements of the model. The following subsections IV.2.11.1 to IV.2.11.4 explain
how the model and corresponding results can be manipulated. The examples presented here have been
tested with Python, COM and .NET assembly.
Example “TESTSAT/RUBY/EX27/readBdf.rb” illustrates the reading of superelements from a BDF file, and the identification of the superelements that have been read.
One first examines a NastranDb object, before reading the model from a BDF file:
db=NastranDb.new()
printf("db = %s\n",db.to_s)
printf(" db.SEID = %d\n",db.SEID)
printf(" db.refCounter = %d\n",db.RefCounter)
printf(" db.NbrSuperElements = %d\n",db.NbrSuperElements)
These instructions produce the following output:
db = DataBase: 0309CDD8 db.SEID = -1 db.refCounter = 1 db.NbrSuperElements = 0
As no model has been read, the number of superelements in the database is necessarily zero. SEID=-1, because the model is not yet “initialized” (read from a BDF or an OP2 file).
The output is different when our example model is read:
db=NastranDb.new()
db.readBdf(bdfPath)
printf("db = %s\n",db.to_s)
printf(" db.SEID = %d\n",db.SEID)
printf(" db.refCounter = %d\n",db.RefCounter)
printf(" db.NbrSuperElements = %d\n",db.NbrSuperElements)
These instructions produce the following output:
db = DataBase: 030BF618 db.SEID = 0 db.refCounter = 1 db.NbrSuperElements = 8
After reading the model, the SEID is set to 0, which means that “db” points to a master DB (corresponding to residual model). The master database contains 8 superelements.
The following instructions:
db2=db.getMaster()
printf("db2 = %s\n",db2.to_s)
printf("db2.class = %s\n",db2.class.to_s)
lead to the following output:
db2 = db2.class = NilClass
As “db” is a master database, the function “getMaster” returns a “nil” object.
On the other hand, the following instructions:
nbr=db.NbrSuperElements
(0...nbr).each do |pos|
printf(" pos = %d\n",pos)
id=db.getSuperElementIdFromPos(pos)
printf(" id = %d\n",id)
sdb=db.getSuperElementFromPos(pos)
if pos==3 then
sdb3=sdb
db2=sdb3.getMaster()
end
GC.start
printf(" sdb = %s\n",sdb.to_s)
printf(" db2 = %s\n",db2.to_s)
printf(" db.SEID = %d\n",db.SEID)
printf(" sdb.SEID = %d\n",sdb.SEID)
if db2 then
printf(" db2.SEID = %d\n",db2.SEID)
end
printf(" refCounter = %d\n",db.RefCounter)
end
produce information for the different superelement databases contained in the master database. For example, for pos=5, the output lines are:
pos = 5 id = 12 sdb = DataBase: 0312C6E0 db2 = DataBase: 030BF618 db.SEID = 0 sdb.SEID = 12 db2.SEID = 0 refCounter = 4
“sdb” points to the superelement at position 5 in the list of superelements. Superelement ID is 12. “db2” is the master database of superelement at position 3 in the list of superelements (fourth superelement as first superelement is at position 0). This means that “db2” points to the master database that has been read from the BDF file.
The database references counter is printed at several places in the script. This has been done to check and debug reference counting. It works as expected with ruby extension. Note however that reference counting management is a little more tricky with Python, .NET assembly and COM component. We made some tests to check these and believe there is no program leak related to reference counting.
The first test with OP2 files involves the reading of Results only. Test is provided in file “RUBY/EX27/readOp2.rb”.
The NastranDb object is initialized by reading model from BDF file as explained in section IV.2.11.1. One builds a list of superelement IDs as follows:
nbr=db.NbrSuperElements seIds=[0] (0...nbr).each do |pos| seIds << db.getSuperElementIdFromPos(pos) end
Note that the master database with SEID=0 is considered in the seIds Array.
Results are read from an OP2 file:
printf("\n\n 0) Reading all the results in the DataBase : \n\n")
db.readOp2(op2FileName,"Results")
The following instructions produce only the title line. No Results are associated to the master database. (This is normal as all GRIDs and elements are defined in superelements and not in the residual model):
printf("\n\n A) Getting results from the main database : \n\n")
db.each_resultKey do |lcName,scName,tpName|
tmpRes=db.getResultCopy(lcName,scName,tpName)
printf("%-20s%-25s%-60s%-10d\n",lcName,scName,tpName,tmpRes.Size)
end
With the following instructions we print the characteristics of Results stored in the master database and all its superelements:
printf("\n\n B) Getting all the results from all databases : \n\n")
seIds.each do |seId|
currentDb=nil
if seId>0 then
currentDb=db.getSuperElementFromId(seId)
else
currentDb=db
end
printf("currentDb.SEID = %d\n",currentDb.SEID)
currentDb.each_resultKey do |lcName,scName,tpName|
res=currentDb.getResultCopy(lcName,scName,tpName)
$stdout.printf("A) %s - %s - %s : %d\n",lcName,scName,tpName,res.Size)
end
end
This produces an output that looks as follows:
B) Getting all the results from all databases : currentDb.SEID = 0 currentDb.SEID = 1 B) Load Case 1 - Statics - Applied Loads, Forces : 8 B) Load Case 1 - Statics - Displacements, Rotational : 88 B) Load Case 1 - Statics - Displacements, Translational : 88 B) Load Case 1 - Statics - Reaction Forces, Forces : 5 B) Load Case 1 - Statics - Reaction Forces, Moments : 5 B) Load Case 1 - Statics - SPC Forces, Forces : 5 B) Load Case 1 - Statics - SPC Forces, Moments : 5 B) Load Case 1 - Statics - Stress Tensor : 256 currentDb.SEID = 2 B) Load Case 1 - Statics - Applied Loads, Forces : 20 B) Load Case 1 - Statics - Displacements, Rotational : 24 B) Load Case 1 - Statics - Displacements, Translational : 24 B) Load Case 1 - Statics - Stress Tensor : 32 currentDb.SEID = 3 B) Load Case 1 - Statics - Applied Loads, Forces : 18 ...
Again, no Result is produced for master DB. On the other hand, superelements contain Results that are retrieved from database using “getResultCopy” method.
We end the example by cleaning the results and erasing the NastranDb object:
db.removeAllResultsAllSE() db=nil GC.start()
A model can also be read from an OP2 file, even though it is not recommended practice. The “readOp2” can also be used to read both the model and Results:
db=NastranDb.new() db.readOp2(op2FileName,"Model/Results")
We verify in the ruby script that the same Results are associated to the master database and its superelements, and that the superelements are correctly read from the OP2 file.
We illustrate how the Results can be retrieved from XDB files when model contains superelements in file “RUBY/EX27/readXdb.rb”. As the model cannot be read from XDB file, database is initialized by reading a BDF file. Results are read into master database and its superelement databases using readXdb method:
printf("\n\n 0) Reading all the results in the DataBase : \n\n")
db.readXdb(xdbFileName)
As master database contains no nodes or elements, no Results are associated to master database, and the following lines produce no output, except the title line:
printf("\n\n A) Getting results from the main database : \n\n")
db.each_resultKey do |lcName,scName,tpName|
tmpRes=db.getResultCopy(lcName,scName,tpName)
printf("A) %-20s%-25s%-60s%-10d\n",lcName,scName,tpName,tmpRes.Size)
end
On the other hand, the following lines produce the same output as the corresponding ruby lines in the “OP2” example in section IV.2.11.2:
printf("\n\n B) Getting all the results from all databases : \n\n")
seIds.each do |seId|
currentDb=nil
if seId>0 then
currentDb=db.getSuperElementFromId(seId)
else
currentDb=db
end
printf("currentDb.SEID = %d\n",currentDb.SEID)
currentDb.each_resultKey do |lcName,scName,tpName|
res=currentDb.getResultCopy(lcName,scName,tpName)
$stdout.printf("B) %s - %s - %s : %d\n",lcName,scName,tpName,res.Size)
if (res.Name=="Displacements, Translational"||res.Name=="Stress Tensor") then
if (bDebug) then
str=format("%s on SEID %d",res.Name,seId)
Util::printRes($stdout,str,res)
end
end
end
end
XDB files can be attached to a NastranDb object:
printf("\n\n 1) Attaching XDB file to the database : \n\n")
db.attachXdb(xdbFileName)
Then, information can be retrieved from XDB file, as is done when no superelement is present in the model. This information can be dependent on the superelement too, so that corresponding superelement database must be used to obtain the information. For example:
sdb3=db.getSuperElementFromId(3) puts sdb3.getAttachmentNodeInfo(xdbFileName,1) puts sdb3.getAttachmentNodeInfo(xdbFileName,2) puts sdb3.getAttachmentNodeInfo(xdbFileName,3) puts sdb3.getAttachmentElementExtId(xdbFileName,7,1) puts sdb3.getAttachmentElementExtId(xdbFileName,7,5) puts sdb3.getAttachmentElementExtId(xdbFileName,7,8)
Remark that the XDB file is attached to master database, but accessed from one of the superelement database.
One obtains information from XDB attachment calling different methods from “db” object:
printf("\n\n C) Attachment information : \n\n")
db.getAttachmentLcInfos(xdbFileName).each do |info|
$stdout.printf("%s%30s%8d%8d%14f%14f\n",
info[0],info[1],info[3],info[4],info[5],info[6])
end
$stdout.printf("nbr load cases = %d\n",db.getAttachmentNbrLoadCases(xdbFileName))
lcNames=db.getAttachmentLcNames(xdbFileName)
scNames=db.getAttachmentScNames(xdbFileName)
resNames=db.getAttachmentResNames(xdbFileName)
puts lcNames,scNames,resNames
Previous lines produce the following output:
C) Attachment information : Load Case 1 Statics 1 101 -1.000000 -1.000000 nbr load cases = 1 Load Case 1 Statics Applied Loads, Forces Applied Loads, Moments Displacements, Rotational Displacements, Translational Reaction Forces, Forces Reaction Forces, Moments SPC Forces, Forces SPC Forces, Moments Stress Tensor
Note that tree “lcNames”, “scNames” and “resNames” Arrays are filled by these instrutions. These arrays are used later in the rest of the script.
Again, no Results can be obtained from the master database, so that the following lines produce no output except the title line:
printf("\n\n D) Getting Attachment results from the main database : \n\n")
lcNames.each do |lcName|
scNames.each do |scName|
resNames.each do |resName|
h=db.getAttachmentResults(xdbFileName,lcName,scName,resName)
if (h) then
h.each do |key,res|
str1,str2,str3=key
$stdout.printf("D) SEID %d - %s - %s - %s : %d\n",db.SEID,str1,str2,str3,res.Size)
end
end
end
end
end
On the other hand, the following lines output Results obtained using “getAttachmentResults” for the superelement databases:
printf("\n\n E) Getting Attachment results from all databases : \n\n")
seIds.each do |seId|
currentDb=nil
if seId>0 then
currentDb=db.getSuperElementFromId(seId)
else
currentDb=db
end
printf("currentDb.SEID = %d\n",currentDb.SEID)
lcNames.each do |lcName|
scNames.each do |scName|
resNames.each do |resName|
h=currentDb.getAttachmentResults(xdbFileName,lcName,scName,resName)
if (h) then
h.each do |key,res|
str1,str2,str3=key
$stdout.printf("E) SEID %d - %s - %s - %s : %d\n",currentDb.SEID,str1,str2,str3,res.Size)
end
end
end
end
end
end
In the same script, one also outputs the characteristics of Results obtained by calling the method “readXdb2H” on master and superelement databases.
As far as Results extraction is concerned, the behaviour of HDF read or attachment functions is very similar to the behaviour of corresponding XDB functions. For example in “RUBY/EX27/readHdf5.rb” script, one prints characteristics of Results obtained from an HDF attachment and from different superelements with the following instructions:
printf("\n\n E) Getting Attachment results from all databases : \n\n")
seIds.each do |seId|
currentDb=nil
if seId>0 then
currentDb=db.getSuperElementFromId(seId)
else
currentDb=db
end
printf("currentDb.SEID = %d\n",currentDb.SEID)
lcNames.each do |lcName|
scNames.each do |scName|
resNames.each do |resName|
h=currentDb.getHdfAttachmentResults(hdfName,lcName,scName,resName)
if (h) then
h.each do |key,res|
str1,str2,str3=key
$stdout.printf("E) SEID %d - %s - %s - %s : %d\n",currentDb.SEID,str1,str2,str3,res.Size)
end
end
end
end
end
end
Most of the “Other tests” have been written to check new developments at some time. They are kept in the list of examples distributed with FeResPost as they illustrate FeResPost capabilities and allow to check new versions of FeResPost.
In the two examples in directory “RUBY/EX24”, we test the correct reading of MPC Forces and MPC Moments when Nastran “Lagrange” option is used for the analysis.
In example “RUBY/EX25/readNonLinear.rb”, we test the reading of nonlinear Results from HDF5 files.
In Examples of directory “RUBY/EX28”, one verifies that the reading of Results at “MPCs” and “MPCNodes” works. This was necessary since on distinguishes MPCs and RBEs in version 5.0.0.
In example “RUBY/EX29/writeGmsh.rb”, one tests the reading of beam stations from BDF files, the correct association of Result key to station node Ids when Results are read from an OP2 file, and the production of GSM Result files at an appropriate output location. To do this, a modifie FEM has been created in “../../MODEL/EXEC_OP2/unit_xyz_stations.bdf”. This FEM includes a modified definition of struts that define different version of intermediate stations for CBAR elements (with CBARAO cards), or CBEAM elements (with appropriate definitions of PBEAML or PBEAM properties).
The GMSH output allows to verify that GMSH markes are generated at the appropriate locations. This is done by plotting Beam Moments in the struts:
strutsGrp=db.getGroupCopy("struts_ALL")
strutsMoments=db.getResultCopy("LAUNCH_ONE_MS2_X","Statics",\
"Beam Moments","Elements",strutsGrp,[])
strutsMoments=strutsMoments*[1.0,0.0,0.0]
Util::printGrp($stdout,"struts",strutsGrp)
Util::printRes($stdout,"Beam Moments",strutsMoments)
...
db.writeGmsh("brol.gmsh",0,[[stress,"stress","ElemCenters"],\
[stress2,"stress2","ElemCorners"],\
[honeyStress,"honeyStress","ElemCenterPoints"],\
[strutsMoments,"beamMoments","ElemNodePoints"],\
[displ,"displ","Nodes"],\
[norm,"norm","Nodes"]],\
[[db.getGroupCopy("pan_PZ"),"mesh pan_PZ"],\
[db.getGroupCopy("pan_MZ"),"mesh pan_MZ"],\
[db.getGroupCopy("pan_PX"),"mesh pan_PX"]],\
[[meshGrp,"skel sat"]],false)
In example “RUBY/EX29/readOp2.rb”, one verifies if the reading of model from OP2 file supports correctly the intermediate stations in CBEAM and CBAR elements. Remember however that reading FEM fronm OP2 file is not recommended. Reading BDF files is safer.
Note that another test for the correct interpretation of the intermediate stations is also done in the post-processing project discussed in chapter IV.4. Then, the purpose is to check whether the post-processing is correct when connections are modelled with CBAR, CBEAM or CBUSH elements and one extracts the corresponding Beam Forces and Beam Moments. Corresponding load cases, envelopes and Results are suffixed with “MOD” to distinguish this test from more normal calculations.
One presents here small examples illustrating the use of FeResPost composite classes. As the classes are still under construction, the examples might be modified in future versions of the program. Also, additional examples will be presented when new feature of the composite classes are available.
The first examples are presented in directory “TESTSAT/RUBY/EX12” and illustrate the importation of data, and the saving of data.
One example is contained in file “testNeutral.rb”. The three first instructions, create a “ClaDb” object and initialize it by reading the ESAComp file “test.edf”. Then the content of the ClaDb object is saved into a neutral file.
dbA=ClaDb.new
dbA.readEdf("test.edf")
dbA.writeNeutral("NeutralA.ndf")
Then, a new “ClaDb” object is created and initialized by reading the previously created neutral file.
dbB=ClaDb.new
dbB.readNeutral("NeutralA.ndf")
dbB.writeNeutral("NeutralB.ndf")
We advise the reader to read and compare the two neutral files. A comparison with ESAComp file might be useful too.
Another example illustrates the possibility of defining a composite database corresponding to the materials and laminates defined in a finite element model. The example is programmed in file “testNastran.rb”. The model DataBase is produced “as usual”. Then the corresponding ClaDb object is returned:
compDb=db.getClaDb
Finally, the composite database is saved in “nast.ndf” neutral file:
compDb.writeNeutral("nast.ndf")
(In this case, the database is not a very interesting one because only one laminate is defined, and it is not a very interesting one.)
The example illustrates the manipulation of objects of the classes defined in FeResPost. The example is presented in directory “TESTSAT/RUBY/EX12”, in file “testCla.rb”.
One first creates a ClaDb and initializes it by reading an ESAComp data file:
db=ClaDb.new
db.Id="testDB"
db.readEdf("test.edf")
Then, a new ClaMat “mat1” is created. Its data are initialized by calls to the appropriate methods, and the material is inserted into the ClaDb:
mat1=ClaMat.new
mat1.Id="mat1"
mat1.Type="isotropic"
mat1.fillModuli({"E"=>72e9,"nu"=>0.33})
mat1.fillCTEs({"alfa"=>2.3e-5})
db.insertMaterial(mat1)
The ClaMat object previously stored into the ClaDb is retrieved into “mat2” variable. The material stiffness matrix is requested and its components are printed:
mat2=db.getMaterialCopy("mat1")
stiffMat = mat2.getStiffness
printf("\n\n stiffMat:\n\n")
stiffMat.each do |line|
line.each do |cell|
printf("%14g",cell)
end
printf("\n")
end
(Similarly, the compliance matrix is printed for the same material.) The following instructions illustrate the creation of a ClaLam object that is stored in the ClaDb:
lam=ClaLam.new lam.Id="testLam" lam.addPly( 1,"mat1",0.00037, 0.0,30e6) lam.addPly( 2,"mat1",0.00037, 45.0,30e6) lam.addPly( 3,"mat1",0.00037,-45.0,30e6) lam.addPly( 4,"mat1",0.00037, 90.0,30e6) lam.addPly(15,"mat1",0.00037, 90.0,30e6) lam.addPly( 6,"mat1",0.00037,-45.0,30e6) lam.addPly( 7,"mat1",0.00037, 45.0,30e6) lam.addPly( 8,"mat1",0.00037, 0.0,30e6) lam.addPly(16,"mat1",0.00037, 0.0,30e6) db.insertLaminate(lam)
Then, characteristics of the laminate like the stiffness and compliance matrices are printed. the following lines illustrate the printing of the laminate ABBD (stiffness) matrix:
ABBD = lam.get_ABBD
printf("\n\n ABBD:\n\n")
ABBD.each do |line|
line.each do |cell|
printf("%14g",cell)
end
printf("\n")
end
Note that the quantities can be printed in any direction wrt laminate axes. For example, the following lines illustrate the printing of laminate thermal expansion coefficient in direction 45 wrt laminate axes:
alfaEh1 = lam.get_alfaEh1(45.0)
printf("\n\n alfaEh1 (45o):\n\n")
alfaEh1.each do |cell|
printf("%14g\n",cell)
end
Similarly, the vector is printed. Finally, the ClaDb is saved into a neutral file. (This neutral file “test.ndf” is used in the other composite examples.)
The example illustrates the calculation of laminate thermal properties. The example is presented in directory “TESTSAT/RUBY/EX12”, in file “testClaTherm.rb”.
The following statements correspond to the introduction of isotropic thermal properties in a material:
mat1=ClaMat.new
mat1.Id="mat1"
mat1.Type="isotropic"
mat1.fillThermalData({"lambdaT"=>170.0,"rho"=>2700.0,"Cp"=>17.0})
db.insertMaterial(mat1)
similarly, one defines an anisotropic material as follows:
mat1=ClaMat.new
mat1.Id="mat_aniso"
mat1.Type="anisotropic"
mat1.fillThermalData({"lambdaT1"=>170.0,"lambdaT2"=>17.0,
"lambdaT3"=>17.0,"lambdaT12"=>0.0,"lambdaT23"=>0.0,
"lambdaT31"=>0.0,"rho"=>50.0,"Cp"=>17.0})
db.insertMaterial(mat1)
The thermal properties stored in a ClaMat object can be printed with the following statements:
lambdaMat = mat2.getInPlaneLambdaT
printf("\n\n lambdaMat:\n\n")
lambdaMat.each do |line|
line.each do |cell|
printf("%14g",cell)
end
printf("\n")
end
printf("\n")
printf(" rho = %g\n",mat2.getRho)
printf(" Cp = %g\n",mat2.getCp)
printf(" rho * Cp = %g\n",mat2.getRhoCp)
One also defines a method that calculates and prints laminate thermal properties:
def writeLamThermalProperties(os,lam,db)
lam.calcLaminateProperties(db)
mat = lam.get_LambdaT
os.printf("\n\n LambdaT:\n\n")
mat.each do |line|
line.each do |cell|
os.printf("%14g",cell)
end
os.printf("\n")
end
os.printf("\n R33T = %g\n",lam.get_R33T)
os.printf(" RhoCpH = %g\n",lam.get_RhoCpH)
end
This method is called with the following statement:
writeLamThermalProperties(STDOUT,lam,db)
In the example of section IV.3.2, one illustrated basically how the composite classes and their methods can be used to calculate composite properties. The example involved the printing of matrices and vectors corresponding to material or laminate properties.
To write the ruby lines devoted to the printing or manipulation of composite entities can be tedious because it is a repetitive task. As for many users, the same composite results are often requested, this may justify the development of Modules or Classes devoted to the most common operations.
One illustrates in this section the extension of the composite classes and of its classes. All these examples are to be found in “TESTSAT/RUBY/EX13” directory.
Presently, only “ClaMat” and “ClaLam” classes have been modified in “extendedCLA.rb”.
One adds methods devoted to the printing of stiffness and compliance matrices, laminate engineering constants... The list of these functions include:
“write_ABBD” for the writing of laminate ABBD stiffness matrix.
“write_abbd_complMat” for the writing of laminate ABBD compliance matrix.
“write_G” for the writing of laminate out-of-plane shear stiffness matrix.
“write_g_complMat” for the writing of laminate out-of-plane shear compliance matrix.
“write_alfaEGh123”, “write_alfaEh2” and “write_alfaEh3”, for the writing of laminate CTE related quantities , , , and .
“write_alfa” for the writing of laminate CTE related vectors , , , , and respectively.
“write_alfaEGh123”, “write_alfaEh2” and “write_alfaEh3”, for the writing of laminate CTE related quantities , , , and .
“write_alfa” for the writing of laminate CTE related vectors , , , , and respectively.
“write_engineering” for the printing of laminate equivalent engineering constants.
Each of these diagnostic functions has two arguments: an ostream object corresponding to the File in which Results are printed, and a Real value corresponding to the angle wrt laminate axes for which the diagnostic is to be written. The following lines show the programming of “write_engineering” method:
class ClaLam
...
def write_engineering(os,theta=0.0)
constants=get_engineering(theta)
tab=["E_xx", "E_k0_xx", "E_f_xx",\
"E_yy", "E_k0_yy","E_f_yy",\
"G_xy", "G_k0_xy", "G_f_xy",\
"nu_xy", "nu_k0_xy", "nu_f_xy",\
"nu_yx", "nu_k0_yx", "nu_f_yx",\
"G_xz", "G_yz"]
counter=0
tab.each do |elem|
if (counter.modulo(3)==0) then
os.printf(" ")
end
str=format("%s = %11g",elem,constants[elem])
os.printf("%25s",str)
counter+=1
if (counter.modulo(3)==0||counter==tab.size) then
os.printf("\n")
end
end
end
...
end # class ClaLam
The programming of the other diagnostic methods is very similar to this one.
The following method writes the laminate load response at laminate level (i.e. no ply results):
def write_loadResponse(os,theta=0.0)
if (!isMechanicalLoadingDefined()) then
raise "No load response has been calculated."
end
if (isThermalLoadingDefined()) then
deltaT=getDeltaT
os.printf(" %14s%14g\n","deltaT",deltaT)
t0=getT0()
os.printf(" %14s%14g\n","T0",t0)
gradT=getGradT
os.printf(" %14s%14g\n\n","gradT",gradT)
end
if (isMoistureLoadingDefined()) then
deltaH=getDeltaH
os.printf(" %14s%14g\n","deltaH",deltaH)
h0=getH0
os.printf(" %14s%14g\n","H0",h0)
gradH=getGradH
os.printf(" %14s%14g\n\n","gradH",gradH)
end
os.printf(" %30s%14s%14s%14s\n","type","XX","YY","XY")
f=getNormalForces(theta)
m=getMoments(theta)
s=getNormalStrains(theta)
c=getCurvatures(theta)
os.printf(" %30s%14g%14g%14g\n","Normal Forces",f[0],f[1],f[2])
os.printf(" %30s%14g%14g%14g\n","Moments",m[0],m[1],m[2])
os.printf(" %30s%14g%14g%14g\n","Normal Strains",s[0],s[1],s[2])
os.printf(" %30s%14g%14g%14g\n","Curvatures",c[0],c[1],c[2])
f=getAverageInPlaneStresses(theta)
m=getFlexuralStresses(theta)
s=getAverageInPlaneStrains(theta)
c=getFlexuralStrains(theta)
os.printf(" %30s%14g%14g%14g\n","Average in-plane stresses",f[0],f[1],f[2])
os.printf(" %30s%14g%14g%14g\n","Flexural stresses",m[0],m[1],m[2])
os.printf(" %30s%14g%14g%14g\n","Average strains",s[0],s[1],s[2])
os.printf(" %30s%14g%14g%14g\n","Flexural in-plane strains",c[0],c[1],c[2])
os.printf("\n %30s%14s%14s\n","type","XZ","YZ")
q=getShearForces(theta)
g=getShearStrains(theta)
os.printf(" %30s%14g%14g\n","Shear Forces",q[0],q[1])
os.printf(" %30s%14g%14g\n","Shear Strains",q[0],q[1])
q=getAverageShearStresses(theta)
g=getAverageShearStrains(theta)
os.printf(" %30s%14g%14g\n","Average shear stresses",q[0],q[1])
os.printf(" %30s%14g%14g\n","Average shear strains",g[0],g[1])
end
Again, in this case, the method has two arguments. Indeed, the components of Laminate load response can be obtained in any direction. Note that this method gives sensible results, only if the “calcResponse” method has been called on the ClaLam object. This remark is valid for all the methods that return information related to a peculiar loading.
The method “write_PliesInPlaneStrainsAndStresses” has only one argument and writes plies in-plane stresses and strains:
def write_PliesInPlaneStrainsAndStresses(os)
if (!isMechanicalLoadingDefined()) then
raise "No load response has been calculated."
end
epsTab=getPliesStrains
sigTab=getPliesStresses
epsMechTab=getPliesMechanicalStrains
os.printf(" %8s%5s","layer","loc")
os.printf("%14s%14s%14s","eps_11","eps_22","gamma_12")
os.printf("%14s%14s%14s","sig_11","sig_22","sig_12")
os.printf("%14s%14s%14s","eps_mech_11","eps_mech_22","gamma_mech_12")
os.printf("\n")
(0...epsTab.size).each do |i|
os.printf(" %8d%5s",epsTab[i][0],epsTab[i][1])
os.printf("%14g%14g%14g",epsTab[i][2],epsTab[i][3],epsTab[i][7])
os.printf("%14g%14g%14g",sigTab[i][2],sigTab[i][3],sigTab[i][7])
os.printf("%14g%14g%14g",epsMechTab[i][2],epsMechTab[i][3],epsMechTab[i][7])
os.printf("\n")
end
end
One also defines methods “write_PliesTemperatures” and “write_PliesMoistures” that write thermal and hygrometric laminate states at ply level. These methods are very similar to “write_PliesInPlaneStrainsAndStresses”.
Correspondingly, the ply failure indices and reserve factors can be calculated and written:
def write_crit(os,db,criteria,fos=1.0) if (!isMechanicalLoadingDefined()) then raise "No load response has been calculated." end if (db==nil) then sdRes=getDerived(criteria) fiRes=getFailureIndices(criteria) rfRes=getReserveFactors(criteria,fos) else sdRes=getDerived(db,criteria) fiRes=getFailureIndices(db,criteria) rfRes=getReserveFactors(db,criteria,fos) end ... end
This last method has several arguments:
“os” specifies where the results are written.
“db” is the ClaDb that is used to calculate failure indices and reserve factors. This argument may be necessary to retrieve plies material allowables and calculate the failure indices. If the argument is nil, then the laminate allowables are used to estimate failure indices.
“criteria” is an Array of strings corresponding to the criteria for which reserve factors and failure indices are requested.
“fos” is an optional argument corresponding to the factor of safety used in the calculation of reserve factors. Its default value is 1.
Note that all the methods added to the ClaLam class perform write operations only. Obviously, methods returning values can also be defined and will ultimately be more useful. But the examples above show that FeResPost is highly customizable and can be adapted to the needs of nearly any user. For example, it should be possible to interface it with graphical packages like ImageMagick or Gnuplot, or with spreadsheets like excel through the win32ole package. Using the Tcl/Tk, it should even be possible to create an interactive program with graphical interfaces.
Similarly, in “ClaMat” class, several printing methods have been defined. A list of these methods follows:
“write_Compliance”,
“write_InPlaneAlfaE”,
“write_InPlaneAlfa”,
“write_InPlaneBetaE”,
“write_InPlaneBeta”,
“write_InPlaneCompliance”,
“write_InPlaneStiffness”,
“write_OOPSAlfaG”,
“write_OOPSAlfa”,
“write_OOPSBetaG”,
“write_OOPSBeta”,
“write_OOPSCompliance”,
“write_OOPSStiffness”,
“write_Stiffness”.
Each of these methods has two arguments: an output stream object, and an optional angle . (Its default value is 0.)
The following example illustrates the use of the new methods in ClaLam class:
require "FeResPost"
require "extendedCLA"
include FeResPost
db=ClaDb.new
db.Id="testDB"
db.readEdf("test.edf")
lam=db.getLaminateCopy("testLam2")
ld=db.getLoadCopy("testFM")
theta=10.0
lam.calcResponse(db,theta,ld,true,false,true)
lam.write_loadResponse(STDOUT,theta)
lam.write_loadResponse(STDOUT,0.0)
STDOUT.printf("\n")
lam.write_PliesInPlaneStrainsAndStresses(STDOUT)
STDOUT.printf("\n")
The main steps of the example are the following:
One first requests the “FeResPost” module and the “extendedCLA” extension of the ClaLam class.
A ClaDb object is created and initialized as usual.
Then, one retrieves the laminate “testLam2” and the load “testFM” from the ClaDb.
The laminate load response is calculated and some results are printed. (Note that the calculation of laminate load response is done first by the call to “calcResponse”.)
The example is contained in the ruby program file “testCla.rb”.
The second example, defined in file “testCla2.rb” illustrates the use of a iterators. For each laminate defined in a ClaDb, one prints several properties. These properties are printed in several directions by rotations of . Part of the program is reproduced below:
def diagnostic(edfName,os)
db=ClaDb.new
db.Id="testDB"
db.readEdf("test.edf")
db.each_laminate do |lamId,lam|
(0..360).step(30) do |i|
theta=1.0*i
os.printf("\nlaminate = \"%s\" -- theta = %g\n\n",lamId.to_s,theta)
os.printf("\n Stiffness matrix : \n\n");
lam.write_ABBD(os,theta)
os.printf("\n");
...
end
end
end
os=File.open("test.txt","w")
diagnostic("test.edf",os)
os.close
The third example, defined in file “testCla3.rb” illustrates the creation of a ClaLoad object and the calculation of corresponding ply stresses and strains. It is reproduced extensively below:
require "FeResPost"
require "extendedCLA"
include FeResPost
db=ClaDb.new
db.Id="testDB"
db.readEdf("test.edf")
tmpLoad=ClaLoad.new
tmpLoad.Id="testF0T"
tmpLoad.setT(20.0)
tmpLoad.setMembrane([0.03,0.0,0.1],"SC","SC","SC")
tmpLoad.setFlexural([0.000000e+00,0.000000e+00,0.000000e+00],"SC","SC","SC")
tmpLoad.setOutOfPlane([100.0,200.0],"FM","FM")
lam=db.getLaminateCopy("testLam2")
lam.setAllPliesIlss(3.0e+7)
lam.setLaminateIlss(3.0e+7)
theta=45.0
lam.calcResponse(db,theta,tmpLoad,true,false,true)
lam.write_loadResponse(STDOUT,theta)
STDOUT.printf("\n")
lam.write_loadResponse(STDOUT,0.0)
STDOUT.printf("\n")
lam.write_PliesInPlaneStrainsAndStresses(STDOUT)
STDOUT.printf("\n")
lam.write_PliesTemperatures(STDOUT)
STDOUT.printf("\n")
criteria=["Tresca2D","VonMises2D","MaxStress","MaxStrain",\
"TsaiHill","TsaiWu","Hoffman","Puck","Puck_b","Puck_c",\
"Hashin","YamadaSun","CombStrain2D","Ilss"]
lam.write_crit(STDOUT,db,criteria)
STDOUT.printf("\n")
This example has been used for mainly debugging composite classes. It illustrates the calculation of failure indices, reserve factors and equivalent stresses in a laminate for a given loading. The reader should examine carefully the result for interlaminar shear.
Note that some criterion may give infinite or NaN values because all the material allowables have not been initialized. (See for example the failure indices of Tresca and Von Mises criteria.)
Another example defined in file “testCla4.rb” illustrates the printing of material matrices and vectors as a function of the orientation. The most important lines look as follows:
mat=db.getMaterialCopy("testPly2")
(0..360).step(15) do |iAngle|
theta=1.0*iAngle
STDOUT.printf("Angle = %g\n\n",theta)
STDOUT.printf(" In-plane compliance matrix :\n\n")
mat.write_InPlaneCompliance(STDOUT,theta)
STDOUT.printf("\n")
STDOUT.printf(" In-plane alfa*E :\n\n")
mat.write_InPlaneAlfaE(STDOUT,theta)
STDOUT.printf("\n")
STDOUT.printf(" In-plane alfa :\n\n")
mat.write_InPlaneAlfa(STDOUT,theta)
STDOUT.printf("\n")
STDOUT.printf(" Out-of-plane compliance matrix :\n\n")
mat.write_OOPSCompliance(STDOUT,theta)
STDOUT.printf("\n")
STDOUT.printf("\n")
end
The first example is presented in directory “TESTSAT/RUBY/EX14” and illustrates the out-of-plane shear calculations. The example is contained in file “testShear.rb”. This example has been developed for debugging purposes and is meant to compare the results of FeResPost with those of ESAComp. After some research one identified what ESAComp does and reproduced its behavior with FeResPost.
One first defines a function that calculations the ESAComp components of out-of-plane shear stiffness matrix kA_44, kA_55, kA_45:
def getESACompG(db,lam,theta)
tmpLam=ClaLam.new
tmpLam.Id="tmpLam"
lam.each_ply do |plyIndex,plyData|
tmpLam.addPly(plyIndex,plyData[1],plyData[2],\
plyData[3]+theta,plyData[4])
end
tmpLam.calcLaminateProperties(db)
shearMat=tmpLam.get_G
ret={"kA_44"=>shearMat[1][1], "kA_55"=>shearMat[0][0],\
"kA_45"=>shearMat[0][1]}
end
The arguments of the function are:
The composite ClaDb in which the materials and laminates definition is stored.
A ClaLam object for which the stiffness matrix components are stored.
A Real object containing the angle by which the laminate is rotated.
The function returns a Hash containing the components of shear stiffness matrix associated to their names. The function works as follows: one defines a new ClaLam identical to the argument ClaLam, except that all the plies are rotated by the argument angle. Then the laminate properties are calculated and the stiffness matrix components are extracted at (default direction in laminate axes for extraction function get_G).
Similarly, one defines a function supposed to return similar values in a more “classical” way (according to FeResPost philosophy):
def getNormalG(db,lam,theta)
lam.calcLaminateProperties(db)
shearMat=lam.get_G(theta)
ret={"kA_44"=>shearMat[1][1], "kA_55"=>shearMat[0][0],\
"kA_45"=>shearMat[0][1]}
end
The methods “getESACompG” and “getNormalG” are used to print the components of shear stiffness matrix according to the two calculation methods and as a function of the orientation . For example, one prints the ESAComp results with the following ruby lines:
os.printf("\n")
os.printf("Laminate stiffness as a function of theta :\n\n")
os.printf("%14s%14s%14s%14s\n","Theta","kA_44","kA_55","kA_45")
(-90..90).step(5) do |i|
theta=1.0*i
ret=getESACompG(db,lam,theta)
os.printf("%14d%14g%14g%14g\n",i,ret["kA_44"],ret["kA_55"],\
ret["kA_45"])
end
os.printf("\n\n")
One observes differences between the results obtained with “getESACompG” and “getNormalG”:
Note that in the “ESAComp” version the angle is the angle by which the laminate is rotated. In the “Normal” version, it is the angle at which the shear stiffness components are recovered (angle wrt laminate axes). So the ESAComp results for an angle should be compared to the “Normal” results for an angle . However in this case the dependence on is even and no difference can be observed.
For angles other than , or , the results obtained with “getESACompG” and “getNormalG” are different. This difference is explained by the approximation:
|
| (IV.3.1) |
|
| (IV.3.2) |
that has been done in section II.1.6.3. The example illustrates one of the consequences of the approximation: the loss of objectivity in out-of-plane shear equations.
One also performs the calculation of out-of-plane shear stresses in laminate for a simple loading in three different directions: , or . Here again the loading is applied in two ways: with the “ESAComp” method or the “Normal” one. For example, the printing of ply stresses with “ESAComp” method is done as follows:
def writeESACompShearStresses(os,db,lam,theta,ld)
tmpLam=ClaLam.new
tmpLam.Id="tmpLam"
lam.each_ply do |plyIndex,plyData|
tmpLam.addPly(plyIndex,plyData[1],plyData[2],\
plyData[3]+theta,plyData[4])
end
tmpLam.calcLaminateProperties(db)
tmpLam.calcResponse(db,0.0,ld,true,false,true)
sigTab=tmpLam.getPliesStresses
os.printf(" %8s%5s%14s%14s\n","Ply","Pos.","tau_13","tau_23")
(0...sigTab.size).each do |i|
os.printf(" %8d%5s",sigTab[i][0],sigTab[i][1])
os.printf("%14g%14g",sigTab[i][6],sigTab[i][5])
os.printf("\n")
end
end
The loading applied to laminate is defined by a pure out-of-plane shear force components and . One also defines a corresponding loading rotated by and defined by its components . This new loading is tested for direction only. The ply stress results obtained with the different versions of loading and calculations methods can be compared and the following comments are made:
Here again, the “ESAComp” results are obtained by rotating the laminate by an angle . For “Normal” results, the loading is rotated by an angle . Therefore “ESAComp” results at are to be compared to “Normal” results at (and vice versa).
When , “ESAComp” results and “Normal” results for a same loading are identical. Otherwise, one observes difference between “ESAComp” results at “Normal” results at (and reversely).
For “Normal” calculation method the loading ld45 at gives the same results as ld at . For “ESAComp” calculation method the loading ld45 at does not give the same results as ld at . “Normal” calculation method is more in line with usual expectations.
Actually, none of the two calculation methods can be considered as better than the other. (At least, as far as the precision of results is concerned.) We think however that “Normal” calculation method is better because it is likely to give unexpected results as shown in the example. Moreover, the associated computation cost is lower. (This will be important when finite element results are post-processed.) Note however, that the “Normal” calculation method also suffers from a lack of objectivity wrt to ply orientations in the laminate.
The examples presented in this section are presented in directory “TESTSAT/RUBY/EX15”.
One presents here an example in which composite classes interact with finite element Result class. One first defines a “bottom” Group containing four elements of the bottom panel, which has a PCOMPG property. A load object, some components of which correspond to finite element Results is defined:
ld=ClaLoad.new
ld.Id="testLoad"
ld.setMembrane([0.03,0.0,0.1],"femFM","femSC","femFM")
ld.setFlexural([0.0,0.0,0.0],"femFM","femSC","femSC")
ld.setOutOfPlane([100.0,200.0],"femFM","femFM")
res=db.getResultCopy("ORBIT_ONE_MS2_Z","Statics","Shell Forces",
"ElemCenters",bottom,[])
res.modifyRefCoordSys(db,"lamCS")
ld.setShellForces(res)
res=db.getResultCopy("ORBIT_ONE_MS2_Z","Statics","Shell Moments",
"ElemCenters",bottom,[])
res.modifyRefCoordSys(db,"lamCS")
ld.setShellMoments(res)
res=db.getResultCopy("ORBIT_ONE_MS2_Z","Statics","Strain Tensor",
"ElemCenters",bottom,["NONE"])
res.modifyRefCoordSys(db,"lamCS")
ld.setShellStrains(res)
res=db.getResultCopy("ORBIT_ONE_MS2_Z","Statics","Curvature Tensor",
"ElemCenters",bottom,["NONE"])
res.modifyRefCoordSys(db,"lamCS")
ld.setShellCurvatures(res)
In the example, no thermal or moisture contribution has been taken into account in the loading. Only mechanical components have been defined. The example, is defined in such a way that all possible mechanical contributions are used: in-plane forces, out-of-plane forces, bending moments, average in-plane strain and curvature. All these components are defined as finite element Results. (This allows us later to compare the Results produced by FeResPost with those directly output by Nastran.) The modification of coordinate system is necessary because one wants the loading components to be expressed in laminate axes. (The Nastran shell forces, moments, curvatures... are given in element axes.)
For later comparison of Results, several Results directly extracted from Nastran “op2” file are directly output in file “Reference.txt”.
os=File.open("Reference.txt","w")
res=db.getResultCopy("ORBIT_ONE_MS2_Z","Statics","Shell Forces",
"ElemCenters",bottom,[])
res.modifyRefCoordSys(db,"lamCS")
Util::printRes(os,"Shell Forces",res)
res=db.getResultCopy("ORBIT_ONE_MS2_Z","Statics","Shell Moments",
"ElemCenters",bottom,[])
res.modifyRefCoordSys(db,"lamCS")
Util::printRes(os,"Shell Moments",res)
res=db.getResultCopy("ORBIT_ONE_MS2_Z","Statics","Strain Tensor",
"ElemCenters",bottom,["NONE"])
res.modifyRefCoordSys(db,"lamCS")
Util::printRes(os,"Strain Tensor",res)
res=db.getResultCopy("ORBIT_ONE_MS2_Z","Statics","Curvature Tensor",
"ElemCenters",bottom,[])
res.modifyRefCoordSys(db,"lamCS")
Util::printRes(os,"Curvature Tensor",res)
res=db.getResultCopy("ORBIT_ONE_MS2_Z","Statics","Stress Tensor",
"ElemCenters",bottom,[])
Util::printRes(os,"Stress Tensor",res)
res=db.getResultCopy("ORBIT_ONE_MS2_Z","Statics","Strain Tensor",
"ElemCenters",bottom,[])
Util::printRes(os,"Strain Tensor",res)
res=db.getResultCopy("ORBIT_ONE_MS2_Z","Statics",
"Composite Failure Index, Tsai-Hill",
"ElemCenters",bottom,[])
Util::printRes(os,"Composite Failure Index, Tsai-Hill",res)
os.close()
As laminate allowables are not defined in Nastran, one modifies the laminate corresponding to the unique PCOMPG property by adding laminate allowables to it. Then the modified ClaLam is reinserted in the database, where it replaces the original one:
lam=compDb.getLaminateCopy(6)
allowables={}
allowables["sc"]=200.0e6
allowables["s1c"]=200.0e6
allowables["s2c"]=200.0e6
allowables["st"]=300.0e6
allowables["s1t"]=300.0e6
allowables["s2t"]=300.0e6
allowables["ss"]=100.0e6
allowables["s12"]=100.0e6
allowables["ilss"]=30.0e6
lam.insertAllowables(allowables)
compDb.insertLaminate(lam)
One also selects the failure indices that shall be calculated. The first one is calculated using ply material allowables, the others with the laminate allowables defined above. For the two last criteria, the most critical layer only is recovered for each element. The definition looks as follows:
criteria = [] criteria << ["TS FI","TsaiHill_c","FI",false,true] criteria << ["TW FI","TsaiWu","FI",true,true] criteria << ["TW FI Critical","TsaiWu","FI",true,false] criteria << ["ILSS FI Critical","Ilss","FI",true,false]
The following call to method “calcFiniteElementResponse” produces Results corresponding to the ClaLam object for which the method is called and writes Results in file “OneLaminate.txt”
theta=0.0
outputs=lam.calcFiniteElementResponse(ClaDb,theta,ld,[true,true,true],
["Shell Forces","Shell Moments", "Shell Curvatures",
"Average Strain Tensor"],
["Stress Tensor","Strain Tensor","Mechanical Strain Tensor"],
1.0,criteria)
os=File.open("OneLaminate.txt","w")
outputs.each do |id,res|
Util::printRes(os,id,res)
end
os.close
The following sequence does the same operation, but the method “calcFiniteElementResponse” is called for the DataBase object “db”.
theta=0.0
outputs=db.calcFiniteElementResponse(compDb,theta,ld,[true,true,true],
["Shell Forces","Shell Moments", "Shell Curvatures",
"Average Strain Tensor"],
["Stress Tensor","Strain Tensor","Mechanical Strain Tensor"],
1.0,criteria)
os=File.open("SeveralLaminates.txt","w")
outputs.each do |id,res|
Util::printRes(os,id,res)
end
os.close
For each element, “db” retrieves the property ID and selects in “compDb” the appropriate laminate with which the calculations are done. Of course, in this case, a single laminate is used and the Results should be the same as when the method is called for the “lam” laminate.
A few remarks can be done about the example:
The example is done with a Group of 4 elements only. This has been done to allow an easy comparison of Results. One could do the example with a Group corresponding to the entire bottom panel to test the efficiency of the method. Also, composite Results can be calculated at corner of elements. (You will discover that the algorithms involved are very efficient, if you do not print the Results.)
The out-of-plane shear stress/strain components retrieved from Nastran OP2 file do not match exactly the values obtained with CLA classes. This is due to limitations of the CLA out-of-plane shear theory that have been highlighted in section II.1.6 of the present document. Results are similar though. Note also that the limitations of the out-of-plane shear theory is general and concerns Nastran as well as FeResPost so that none of the two results is really better than the other one.
In the example, one tries to compare Results calculated directly with Nastran with those produced by FeResPost. This is one possible use of the “calcFiniteElementResponse” method, but not the only one. For example:
One can produce Results corresponding to deteriorated allowables due to manufacturing problems, or ageing...
Some calculation methods require modification of the loadings. sometimes, for example, curvature is neglected, or only partially taken into account for the calculations.
Also, with Nastran, composite Results can be produced, even when no laminate (PCOMP) properties have been modeled. This is the case when equivalent shell properties are modeled.
...
The examples given above are far from being exhaustive. The stress engineers experienced in composite calculations will very soon discover the advantages of the new method. This is particularly true when Nastran is used because its composite capabilities are poor. (Even though Patran compensates partially Nastran deficiencies with its optional “Laminate Modeler” tool.)
A simplified variant of the example is presented in “testCriteria.rb” file. There the failure indices are calculated using directly layered stresses read from Nastran op2 file. For example, one calculates the failure indices using the ClaLam method as follows:
outputs=lam.calcFiniteElementCriteria(compDb,stressRes,1.0,criteria)
The example illustrates the manipulation of CLA objects units. The example is presented in directory “TESTSAT/RUBY/EX18’, in file “testMatUnits.rb”.
The sequence of operations is simple:
A DataBase is read from neutral file “”.
Then engineering constants of all the laminates in the DataBase are saved into file “oldUnits.txt”.
The units of all materials in the DataBase are modified using method “changeUnitsAllMaterials”.
The modified DataBase is saved into file “testUnits.ndf”.
Then engineering constants of all the laminates in the modified DataBase are saved into file “newUnits.txt”.
The two files “oldUnits.txt” and “newUnits.txt” may be compared. They should contain equivalent results.
The part of interest of the example is the modification units for all the materials in the database:
oldUnits=db.getUnits newUnits=oldUnits.clone newUnits["F"]="lbf" newUnits["L"]="mm" newUnits["T"]="oF" puts oldUnits puts newUnits db.each_material do |id,mat| mat.changeUnits(newUnits) db.insertMaterial(mat) end
(Note that in the example, one deliberately decided not to use the “changeUnitsAllMaterials” method of the ClaDb class.)
The user may test the outputs with or without units systems modifications to verify if the results are affected by the modification of units. (They should not be modified.)
We present in this chapter an example of object-oriented post-processing programmed in ruby language. The structure of the post-processing presented here is very similar to the structure of post-processings we are currently using on actual “real” projects, and results from a long evolution driven by years of practice. Earlier versions of the post-processing project are presented and discussed in Appendixes X.D.2 and X.E.4 and in Chapter VII.4.
We summarize below the history of post-processings that are described in FeResPost User Manual:
The first post-processing project that has been written in ruby if the modular post-processing presented in Appendix X.D.2. The project is written in ruby language, but is not object-oriented, which is a shame.
Therefore, a second version of the post-processing, also with ruby language, has been programmed. This post-processing is more object-oriented, and is described in Appendix X.E.4. It suffers however several limitations. One of these limitations, is that one single post-processing object can be related to the calculation of several parts of interfaces. This corresponds actually to a limitation of the object-orientation of post-processing objects.
An excel post-processing is presented in Chapter VII.4. The programming is then done with VBA language, and FeResPost COM component is used. This post-processing is a nice example of excel automation with FeResPost COM component. One discovered however several limitations of this excel when using it on large projects:
Important limitations are related to the programming with VBA language which is a little too old fashioned to produce an efficient code. In particular, VBA language is only slightly object-oriented. This results in difficulties to produce efficient code. The modifications of existing code is also more difficult with VBA language than with other languages.
There is no clear separation of programming and data, as the triggering of post-processing is done via the calculation of functions in excel spreadsheets. In particular, the fact that each failure criterion is calculated via the calculation of an excel function, limits the possibility to optimize the project by reducing the number of Results extractions from Nastran Result files.
In my company, we have access to 32 bits versions of Office only. This limits the size of XDB files that can be used to approximately 2Gb. Also, excel is run on computers with limited power and RAM. This is sometimes a big problem as the computer is also used for other purposes when the post-processing is run.
Finally, a new post-processing has been programmed in ruby. This post-processing inherits most of the best characteristics of the previous versions presented in Appendix X.E.4 and Chapter VII.4. This post-processing is described in the rest of current Chapter.
The rest of this Chapter is organized as follows:
Section IV.4.1 is devoted to the general structure of the project. One also describes the main classes and modules that define the programming of the post-processing.
Section IV.4.2 describes how the data have been defined for the example.
Several tools for the final post-processing steps are described in section IV.4.3.
Note that the purpose of current chapter is to describe the main structure of the post-processing in a way that allows the reader to better understand source code. However, the understanding of the project will be achieved only by diving into the source code, which is described in section IV.4.1.
“DbAndLoadCases” module also acts as a server of Results for the post-processing objects discussed in section IV.4.1. Method “DbAndLoadCases.getResult” is programmed in such a way that the post-processing classes remain “unaware” of the solver or solution sequence that have produced the Results being post-processed:
Post-processing objects do not know whether they post-process Nastran or Samcef Results.
When Nastran Results are post-processed, they do not know whether these Results have been extract from OP2, HDF or XDB files.
When accessing Results stored in current FEM database, they require Results using the “real” Result names, without “ (MP)” or “ (RI)”. Manipulations specific to Result format is done inside post-processing objects however.
We made reference above to the excel post-processing described in Chapter VII.4. Current project also uses Microsoft Office tools:
To produce the CSV files that define the post-processing data. Indeed, excel is an handy tool to present and manipulate tables.
To extract results from the “xl_*” tables in SQLite database and save them in separate excel Workbooks.
To copy and paste automatically tables from excel to word. Writing of parts of the reports can then be automated.
More informations about the final part of post-processing is provided in section IV.4.4. Note that the use of Microsoft Office tools, excel in particular has been reduced as much as possible in order to allow the running of most post-processing on Linux instead of Windows. This is why excel is used only for the preparation of CSV files, and for the extraction of results to be inserted into Word reports.
The post-processing project we are describing here does no use excel. It can be run on Windows computers as well as Linux computers. It requires only the following programs:
Ruby program must be installed on the computer. One suggests a 64 bits version of the program as it allows random access to larger result files, and the use of larger memory for the calculations and storage of objects.
FeResPost must of course be also installed on the computer.
As excel can no longer be used for the storage of post-processing results, one uses SQLite. The corresponding ruby extension must be installed.
All the classes and modules defined here are defined in “PROJECT/PGR” sub-directory.
Module “DbAndLoadCases” is devoted to the management of FEM databases and load cases. Three classes are defined in the module:
class “DbAndLoadCases.DB” stores the data used for the one FEM dataBase definition. In the project, FEM dataBases can correspond to Nastran or Samcef models. The different FEM dataBases are stored in “DbAndLoadCases.databases’ member data. A database is created and stored simply with instructions like:
db=DbAndLoadCases::DB.new(dbName,"NASTRAN",bdfFileName,
sesFileNames,claDbs,gmshFileName)
DbAndLoadCases.databases[dbName]=db
(See source code and examples for a description of the arguments of “DbAndLoadCases::DB.new” method.)
Class “DbAndLoadCases.ElemLc” is devoted to the storage of elementary load cases. An elementary load case corresponds to a set of results that can be directly accessed from a Nastran or Samcef result file by identification of its load case and sub-case names. An elementary load case is created and stored in the module as follows:
lc=DbAndLoadCases::ElemLC.new(name,dbName,resFileType,resFileName,
resFileLcName,resFileScName)
DbAndLoadCases.elemLoadCases[name]=lc
Class “DbAndLoadCases.CombiLC” is used for the management of combined load cases. More precisely, this class allows the creation of Results obtained by linear combinations of elementary load cases Results, already loaded into a FEM dataBase. A combined load case is defined with instructions like:
lc=DbAndLoadCases::CombiLC.new(lcName,factors,elemLcNames)
DbAndLoadCases::combinedLoadCases[lcName]=lc
Note that a limitation of post-processing project, is that the elementary load cases used for the definition of a combined load case must be loaded in a single FEM dataBase.
All the static load cases that have been defined in “DbAndLoadCases” module are not necessarily post-processed. The list of static load cases to be post-processed is specified via following instructions:
DbAndLoadCases.addOneSelection(lcName,params)
The definition of databases, elementary and combined load cases, and of the selection of static load cases are a preliminary step in the post-processing project. This means that corresponding entities must be defined before the loop on static load cases which looks as follows:
DbAndLoadCases.loopOnStaticCases() do |lcName|
puts lcName
postList.each do |p|
begin
p.initCalcSteps()
p.calculate("Static")
rescue Exception => x then
printf("Failed Post object %s with ID %s\n",p.to_s,p.postID())
PrjExcept.debug(x)
end
end
DbAndLoadCases.saveMosResults(postList)
DbAndLoadCases.saveSrResults(postList)
end
For dynamic load cases (post-processing of Nastran SOL 111 analysis), no elementary or combined load cases are defined. Instead, the loop on the different sub-cases is done via instructions that look as follows:
db=DbAndLoadCases::DB.new(dbName,"NASTRAN",bdfFileName,
sesFileNames,claDbs,gmshFileName)
DbAndLoadCases.databases[dbName]=db
DbAndLoadCases.prepareDataBase(dbName)
DbAndLoadCases.loopOnDynamSubCases(resFileType,resFileName,
lcName,fMin,fMax,scNbrMax) do |lcNameA,lcNameB|
puts lcNameB
postList.each do |p|
begin
p.initCalcSteps()
p.calculate("Dynamic Complex")
rescue Exception => x then
printf("Failed Post object %s with ID %s\n",p.to_s,p.postID())
PrjExcept.debug(x)
end
end
DbAndLoadCases.saveMosResults(postList)
DbAndLoadCases.saveSrResults(postList)
end
(The loop on sub-cases is obtained via an iterator directly defined in “DbAndLoadCases” without defining “ElemLc” or “CombiLc” objects.) Note that, another iterator is associated to dynamic (complex) results:
DbAndLoadCases.iterateOnTheta(currentLcName,bakResults) do |srLcName,mosLcName,results| # One performs the calculations with the Real results : @step_1_results=results calc_2(srLcName,mosLcName) end
This iterator produces real Results from the complex Results , corresponding to different phases. (In out post-processing 12 phases are considered for each output frequency.) This iterator is called by the “calculate” method defined in “GenPost” class described in section IV.4.1.2.
“DbAndLoadCases” module also defines the methods that can be used to store results in an SQL database:
Method “DbAndLoadCases.getOutputSqlDb” is used to open (and create if necessary) the SQL database into which results are stored. Method is simply called as follows:
DbAndLoadCases.getOutputSqlDb("OUTPUTS/results.db3")
(The link to SQL database is stored in the “DbAndLoadCases” module.) Note that when the dataBase is created several SQL tables and views are also created in the database.
“DbAndLoadCases.saveMosResults” method is used to store post-processing results in the “excel-like” tables of SQL database. The argument of the function is an Array containing a list of post-processing objects. (See section IV.4.1.2.)
“ DbAndLoadCases.saveSrResults” method is used to store Strength Ratios in the “StrengthRatios” table of SQLite database. (See section IV.4.1.2 for the definition of Strength Ratios concept.)
The iterators on static and dynamic load cases also save load case or subcase information in “loadCasesInfos” table.
Note that “DbAndLoadCases” module is unaware of SQLite. All interactions with SQL database are done via “SqlWrap” module discussed in section IV.4.1.3. This has been done to ease the swap from SQLite to another SQL database system.
All the post-processing classes derive from the generic “GenPost” class defined in file “PGR/post.rb”. A post-processing object performs the calculation of a one or several criteria on a specific structural part or interface. It then manages the following operations:
Initialization and storage of the data defining the post-processing object.
Method “calc_0” generally performs the extraction of Results from the active FEM database. This method is defined in base “GenPost” class, but will generally be re-defined in all the specialization classes. Extracted Results are stored in @step_0_results member data.
Method “calc_1” performs linear operations on extracted Results, or operations that are not specific to the calculation of a failure criterion. Corresponding Results are stored in @step_1_results member data.
Method “calc_2” performs the calculation of failure criteria, which generally involve non-linear calculations. Corresponding Results are stored in @step_1_results member data.
Method “calculate” chains the three calculation steps. For static load cases, the chaining is done as follows:
when "Static" then
calc_0()
calc_1()
srLcName=currentLcName
mosLcName=currentLcName
if self.respond_to?("calc_2") then
calc_2(srLcName,mosLcName)
end
@step_0_results = {}
@step_1_results = {}
@step_2_results = {}
Remark that one tests that “calc_2” method is defined as this method is not defined in “GenPost” base class, and not necessarily defined in derived classes. For the dynamic load cases, that produce complex Results, the chaining is done as follows:
calc_0()
calc_1()
# calc_2 not necessarily defined in sub-classes :
if self.respond_to?("calc_2") then
lcNameA=currentLcName
# One backups the complex results and uses them as argument in iterator :
bakResults=@step_1_results
DbAndLoadCases.iterateOnTheta(currentLcName,bakResults) do |srLcName,mosLcName,results|
# One performs the calculations with the Real results :
@step_1_results=results
calc_2(srLcName,mosLcName)
end
end
@step_0_results = {}
@step_1_results = {}
@step_2_results = {}
Here again, the existence of “calc_2” method in the Post object is tested. One also remarks that the iteration on the different phases is done inside the “calculate” method by calling “DbAndLoadCases.iterateOnTheta”. This method produces real results from complex ones. Indeed, “calc_2” methods defined in derived classes can deal with real Results only.
Method “getParam” is used in the post-processing specialization classes to obtain parameters. Parameters can be defined at different levels. Function “getParam” looks for the parameters in the following order:
In the “@parameters” Hash member data of “GenPost” class.
In the “critParams” Hash optional argument the “getParam” method.
in the parameters associated to current laod cases, and that are retrieved with “DbAndLoadCases.getParam(paramName)” instruction.
“getParam” method has two arguments:
A String corresponding to the name of the parameter.
An optional Hash argument corresponding to the list of parameters associated to a criterion.
Different methods are related to the the management of @mosResults and @srResults member data. Among these methods, only the “updateSrResults” method present some complexity as one of its purposes is also to aggregate the strength ratios produced by different post-processing objects.
The different member data of “GenPost” class deserve some explanation as well:
“@step_0_results” is a Hash that associates a String Result name, to a Result object. These Results by “calc_0” method.
“@step_1_results” is a Hash that associates a String Result name, to a Result object. These Results by “calc_1” method.
“@step_2_results” is a Hash that associates a String Result name, to a Result object. These Results by “calc_2” method, when applicable.
“@mosResults” is used to store temporarily results to be saved in excel-like SQL Tables. This variable contains an Array of which each element is an Array of 4 elements:
A String corresponding to the name of the SQL table in which results will be saved. This String is defined when post-processing object is initialized. It is not “hard-coded” in post-processing class code.
A String containing the SQL statement for table creation.
A String containing the SQL statement for insertion in table.
An Array corresponding to the values to be inserted in the SQL table.
In the end, each “@mosResults” element should correspond to a line saved in an SQL table.
“@srResults” is used to store temporarily the Strength Ratios for later archiving in SQL database. Storage is done in a Hash object. Each key is an Array of 4 Strings corresponding to:
A load case name,
The name of a GMSH file,
A GMSH result name,
A location or FEM association (for example “ElemeCenters”, “ElemCorners”, “Nodes”...).
The value associated to each key is a Result object (normally a real scalar one).
The reader will have understood that the purpose of saving Results in a temporary variable is to prepare the production of GMSH files for the visualization of Strength Ratios. A Strength Ratio is a Result object corresponding to the inverse of RF, but mapped to part of the structure.
Note that the “Post” classes have been programmed in such a way that they remain, as much as possible “unaware” of the peculiar solver that has is used to produce the results that are post-processed. In particular:
“calc_0” and “calc_1” steps should not care whether the Results that are post-processed are real or complex. Or when it matters, the format of Results should be tested to be managed by appropriate code.
The example “Post” objects should work as well with as with Nastran Results. When post-processing Nastran Results, the reading of Results from OP2, HDF or XDB file is not supposed to produce different outputs. Practically, this behaviour is obtained by accessing FEM results via calls to “DbAndLoadCases.getResult” method.
Note also that the Result names used to specify to “DbAndLoadCases.getResult” method which Results are requested are always real Result names. (There is no “ (MP)” or “ (RI)” involved.) “DbAndLoadCases.getResult” method manages a mapping that allows to access the relevant complex Results when needed.
The classes inheriting “GenPost” class are listed below.
This class is devoted to the post-processing of “Stress Tensor” Results. It proposes several failure criteria corresponding to Von Mises or core justification. For a single “Stress Tensor” Result extraction, several failure criteria can be calculated, and parameters specific to each failure criterion are defined in the data for this failure criterion. A “PostCauchyStress” object is created as follows:
p=PostCauchyStress.new() p.setData(partName,loc,grpName,layers,criteria,params)
The parameters of “setData” method are explained in Table IV.4.1. We consider it is user’s responsibility to write the code builds the post-processing objects with appropriate parameters. (See examples of definitions of data in section IV.4.2 for more details.)
This class is devoted to the calculation of composite failure criteria via the classical laminate analysis. Here also, several criteria can be calculated by each “PostLaminate” object, but always for a single calculation of Stress or Strain Tensor Result.A “PostLaminate” object is created as follows:
p=PostLaminate.new() p.setData(partName,loc,grpName,layers,criteria,params)
The parameters of “setData” method are explained in Table IV.4.2. We consider it is user’s responsibility to write the code builds the post-processing objects with appropriate parameters. (See examples of definitions of data in section IV.4.2 for more details.)
This class is devoted to the justification of connections. It presents several failure criteria corresponding to sliding of interfaces, gapping,failure of inserts, failure of bolts (according to method proposed in [otNCE21]), failure by bearing... A “PostConnect” object is created as follows:
p=PostConnect.new() p.setData(ifName,params)
The parameters of constructor method are explained in Table IV.4.3. We consider it is user’s responsibility to write the code builds the post-processing objects with appropriate parameters. (See examples of definitions of data in section IV.4.2 for more details.)
Note that:
Each criterion is associated to its own specific parameters.
For the failure of bolts, the programming of failure criterion according to NASA-STD-5020 makes use of the predefined interaction criterion “Interaction_abg_N_SR” discussed in section X.D.1.6.
| Parameters for the extraction of Stress Tensor (“setData” parameters)
| ||
| ifName | String | The name of the interface to which Excel results will be associated |
| type | String | Description of the type of connection saved in Excel table of results. This parameter does not influence the calculation. |
| interfaceDef | Hash | This Hash contains information regarding the interface definition and how connection loads are retrieved from FEM results. Additional information is given below in te Table. |
| criteria | Array | The different extraction or failure criteria that will be processed at step 2 (or step 1 for “GlobFM” extraction). |
| How the “interfaceDef” Hash parameter defines the interface... Defines the extraction
source and method, possible modification of coordinate system, direction vector for
connection axis, optional parameters for bolt group redistribution of connection loads, ...
Optional parameters are in parentheses.
| ||
| ifName | String | The name of the interface for which connection loads are extracted. This should match the “ifName” argument of “setData” method discussed above. |
| grpNameA | String | The name of Group “A” defining the interface. |
| grpNameB | String | The name of Group “B” defining the interface. This second Group is not necessarily used but parameter is requested. It can be set to nil if the extraction method does not require Group “B”. |
| method | String | Identifies the loads extraction method. Possible values are “BMFRC”, “BSHFRC”, “GPFINT”, “GPFMPC”, “GPFSPC”, “MPCFRC”, “SPCFRC” and “APPFRC”. This corresponds to the specification of entities on which forces and moments are extracted. (See the sources of “PostConnect” class if you have doublts regarding the meaning of these parameters.) |
| csId | String or Integer | Specification of the coordinate system in which interface load components must be expressed before deriving axial forces, shear forces, bending moments... |
| direction | Array | Array of three Real values specifying connections’ axis. Components of this vector are given wrt the coordinate system identified by “csId” above. |
| bRedistr | Boolean | Specifies whether a bolt group redistribution is requested. The parameters that follow are optional and must be provided only if a bolt group redistribution is requested. (Theory is given in Appendix X.G.2.5.) |
| (bgCsId) | Integer | Identification of the coordinate system for bolt group redistribution |
| (kT) | Real | Translational stiffness of connections for bolt group redistribution |
| (kR) | Real | Rotational stiffness of connections for bolt group redistribution |
| (grpName3) | String | Name of a group of nodes defining the locations of connections onto which global loads are redistributed. If this argument is nil, the redistribution is done on locations corresponding to the FEM entities from which loads are extracted. |
| Criteria and their parameters
| ||
| Each criterion is defined in an Array of 5 elements
| ||
| critName | String | Name of the criterion |
| gmshFileName | String | GMSH file name |
| gmshResName | String | GMSH result name |
| xlTableName | String | Name of the Excel worksheet in which results will be saved |
| critParams | Hash | Parameters for the derivation of criterion. (See below.) |
| The different extraction or failure criteria are generally calculated in “calc_2” method of
the post-processing object. “GlobFM” extraction criterion is the exception as this one is
calculated at in “calc_1” method.
| ||
| Parameters if critName =“GlobFM”
| ||
| csId | Integer | Specifies the coordinate system considered for the calculation of interface global force and global moment. Note that this coordinate system may differ from the coordinate system specified in interface definition above, even though we use the same “csId” Hash key. |
| refPoint | Array | Array of three Real values specifying the coordinates of the point wrt which global force and moment are calculated. Coordinates are given wrt to coordinate system specified by “csId” above. |
| format | String | Specifies the format in which results are saved in Excel table. Possible values are “R”, “RI” or “MP”. This parameter matters when complex Results are post-processed (SOL 111 analysis). |
| This extraction is done in “calc_1” method. This is because for the post-processing of SOL
111 interface results the results are complex and one performs an extraction of complex
components instead of one extraction for each phase that is post-processed.
| ||
| Parameters if critName =“Sliding”
| ||
| FoS | Real | Safety Factor |
| Pmin | Real | Minimum value of bolts’ pretension |
| Cf | Real | Friction coefficient between assembled parts |
| Parameters if critName =“Gapping”
| ||
| FoS | Real | Safety Factor |
| Pmin | Real | Minimum value of bolts’ pretension |
| Lg | Real | Prying length for bending moment contribution |
| Parameters if critName =“Insert”
| ||
| FoS | Real | Safety Factor |
| PSS | Real | Insert tensile allowable |
| QSS | Real | Insert shear allowable |
| Parameters if critName =“PullThru”
| ||
| FoS | Real | Safety Factor |
| PSS | Real | Insert tensile allowable |
| Parameters if critName =“ShearBearing”
| ||
| FoS | Real | Safety Factor |
| QSS | Real | Insert shear allowable |
| Parameters if critName =“IfLoads”
| ||
| No parameter are provided for this criterion. (“critParams” is an empty Hash.) The failure
criterion saves load components as they have been extract from FEM Results, according
to “interfaceDef” Hash parameters. (See above in the table.)
| ||
| Parameters if critName =“NasaStd5020”
| ||
| FoS | Real | Safety factor |
| D | Real | Connection diameter. (Does not seem to be used in calculation of failure criterion.) |
| Lg | Real | Prying length considered to account for the bending moment |
| hsp | Real | ... |
| etaPhi | Real | ... |
| Pmax | Real | Maximum bolt pretension |
| Pt | Real | Bolt tensile allowable |
| Ps | Real | Bolt shear allowable |
| Pb | Real | Bolt bending allowable |
| bSpInThreads | Boolean | True if the shear plane is in threaded part of fastener |
| bPrldCombined | Boolean | True if the preload is considered in fastener shear or combined failure analysis. (According to section A.7 of [otNCE21], this preload can be neglected for some failure modes.) |
| Parameters if critName =“NasaStd5020_DBG”
| ||
| This criterion is used for debugging purpose only and very close to “NasaStd5020’´.
Corresponding parameters may be modified without notification and are therefore not
described here.
| ||
This method performs simple extractions of results, to be archived in excel-like SQL tables, but without actual calculation of failure criteria. This is an example of post-processing class in which no “calc_2” method is defined. Also, this class does not fill the “@srResults” member data.
Two classes provide various utilities. See below.
“Util” module provides following methods. We list below the main methods:
“Util.printRes” method can be used for debugging post-processing.
“Util.printGrp” method can be used for debugging post-processing.
“Util.printDbResList” method can be used for debugging post-processing.
“Util.printDbGrpList” method can be used for debugging post-processing.
“Util.iter_csv” method is used to scan the lines of a CSV file. Each line is translated to an Array of Strings. This method is used to define the post-processing objects. (See section IV.4.2.)
“Util.convert_csv_line” method is used to convert an Array of String obtained by reading a CSV file, to an Array of values according to specified types. This method is used to define the post-processing objects. (See section IV.4.2.)
“Util.ensureDirectoryForFile” method creates, if necessary, a directory prior to creating a file in that directory.
This class is very short. It is wrapping around SQLite::database class, and has been introduced in such a way that all SQL code specific to SQLite is contained in this class. The purpose of this class is to ease the transfer of post-processing project to another SQL database system, if necessary. The class proposes only three methods: “initialize”, “execute” and “timeStamp”.
Most of the definition of data is done by functions defined in “PROJECT/DATA” sub-directory. The main data files are directly located in “PROJECT’ main directory however. The main data files are:
“static.rb” that manages the data for the static thermo-elastic and mechanical load cases.
“dynam.rb” that performs the operations needed dor the post-processing of SINE load cases (Nastran SOL 111 analyses).
The “post.rb” script that performs final operations leading to the calculation of Strength Ratio envelopes, and the output of GMSH visualization files. (See section IV.4.3.)
Data are interpreted by calling different ruby methods and build different kinds of objects:
The definition of post-processing objects is done by calling functions defined in four ruby source files called “postExtractData.rb”, “postInterfaceData.rb”, “postSandwichData.rb” and “postStressData.rb”. Each of the four functions that is called builds a list of specific post-processing object (instanciations of classes they derive from “GenPost”), that is returned in an Array.
In general, the post-processing object is instanciated and initialized according to values read from a CSV file. The CSV files are located in “PROJECT/DATA/CSV_POST” directory. In “PROJECT/static.rb” main source file, the post-processing objects are build by the following calls:
postList=[]
postList+=getAllStressData()
postList+=getSandwichData()
postList+=getInterfacePostData()
postList+=getStaticExtractData()
“Static” module also defines an iterator that is just a “wrapper” around another iterator defined in “DbAndLoadCases” module. This wrapper iterator looks as follows:
def Static.loop()
DbAndLoadCases.loopOnStaticCases() do |lcName|
yield lcName
GC.start()
end
end
It is called from the main ruby file “PROJECT/static.rb” as follows:
Static.loop do |lcName|
puts lcName
postList.each do |p|
begin
p.initCalcSteps()
p.calculate("Static")
rescue Exception => x then
printf("Failed Post object %s with ID %s\n",p.to_s,p.postID())
PrjExcept.debug(x)
end
end
DbAndLoadCases.saveMosResults(postList)
DbAndLoadCases.saveSrResults(postList)
end
(Note that we could have called “DbAndLoadCases.loopOnStaticCases()” iterator directly.)
The definition of static load cases data is done by calling different functions of “Static” module defined in “PROJECT/DATA/staticLoadCasesData.rb”. The main function of this module is “Static.readDbAndLcDefs” that reads a CSV files that contains information that allows to build FEM databases, elementary and combined static load cases. Another important method is “Static.readLcSelection” that reads a selection of load cases from another CSV file and associates parameters to these load cases. In our example, the CSV files are located in directory “PROJECT/DATA/CSV_LC”.
In “PROJECT/static.rb” main source file, the building of the databases and load cases is done via the following line:
Static.setFemDirName("D:/SHARED/FERESPOST/TESTSAT/MODEL")
Static.readDbAndLcDefs("DATA/CSV_LC/DbAndLoadCases.csv")
Static.readLcSelection("DATA/CSV_LC/Selection.csv")
The details of the data are found in the CSV files.
For dynamic load cases, that correspond in our examples to the results of a SINE calculation, the database and the loop of load cases is defined directly in the main ruby file “PROJECT/dynam.rb”. For example, the loop one the different frequencies look as follows:
lcNames=["SINUS_X","SINUS_Y","SINUS_Z"]
#~ lcNames=["SINUS_X"]
resFileType="HDF"
resFileName=femDirName+"/EXEC_HDF5/sol111_ri_xyz_corners.h5"
fMin=-1.0
fMax=10000.0
#~ fMax=53.1
lcNames.each do |lcName|
DbAndLoadCases.loopOnDynamSubCases(resFileType,
resFileName,lcName,fMin,fMax,scNbrMax) do |lcNameA,lcNameB|
puts lcNameB
postList.each do |p|
begin
p.initCalcSteps()
p.calculate("Dynamic Complex")
rescue Exception => x then
printf("Failed Post object %s with ID %s\n",p.to_s,p.postID())
PrjExcept.debug(x)
end
end
DbAndLoadCases.saveMosResults(postList)
DbAndLoadCases.saveSrResults(postList)
end
end
(The trick is to provide the appropriate parameters to the
“DbAndLoadCases.loopOnDynamSubCases” iterator method.)
The idea of using CSV files to store the definition of parameters is a legacy from the excel post-processing described in Chapter VII.4. It is also a very effective way to define the data. It improves the readability of data definition, and data definition in a combination of ruby code and CSV files ensures the flexibility needed to deal with specific cases.
Note that one of the post-processing data definition function does not involve the reading of a CSV file: “getSandwichData” method defines all the data in ruby code. This has been done because only one corresponding instance is created in the project. However, in more normal circumstances, it would be advantageous to define the data in a CSV file as well.
In general, the meaning of a parameter in a CSV file depends on the index of the column in which it is defined. Then, it is the responsibility of user to verify that the in each CSV data line, each value is inserted in the appropriate column, so that ruby code that interprets CSV lines fills the appropriate parameters for the construction of each “postConnect” object.
For the post-processing of connections, the CSV file “Interfaces.csv” that defines the data is formatted following conventions that differ from those adopted for the other types of post-processing criteria. Correspondingly the ruby method that reads the CSV lines and interprets them works differently. The CSV file is characterized by the insertion of directive lines that start with a keyword and specify how the following CSV lines must be interpreted:
Directive “COLTYPES” specifies the type of each column in following CSV data lines. “s” corresponds to “string”, “i” to integer, “f” to real...
Directive “COLNAMES” defines the name associated to each column. This name is used to identify what each column corresponds to. It is used by ruby function to find the different parameters needed for the building of “post” objects.
Directive “COLUNITS” is not interpreted by the method but helps the user to remember the units associated to each value in a CSV line.
Directive “COLFACTORS” specifies factors applied to the corresponding real values in data CSV lines. If Nastran calculation is done with IS units, the post-processing should consider the same IS of units. Then, for example, if data are specified in millimeters, they should be converted to meters in post-processing calculations.
If the cell in column “A” of a line is not empty and does not corespond to one of the keywords above, the line defines values that are used for the definition of a “postConnect” object. These values are interpreted considering the last “COLTYPES”, “COLNAMES” and “COLFACTORS” instructions in rpreviously read lines.
An example of CSV lines with interpretation directives is presented in Figure IV.4.1. (Directive keywords are coloured in red in the excel worksheet.) We observe that the factor 0.001 is always associated to data specified in millimeters. This corresponds to the conversion of these values to meters.

The approach for connection “post” objects construction is more flexible. It allows to consider several formats for the different lines of a CSV file. This is particularly appropriate for the definition of connection “post” objects, because the post-processing failure criteria may differ significantly depending on the interface considered.
In the post-processing example, all the outputs are saved in a single SQLite database. Some of the results can be accessed interactively via “SQLiteAdmin” program. This is for example the case for the excel-like tables in the database. SQLiteAdmin program allows to create views, export tables or views in excel. This means that part of the results saved in the database can directly be used to assess structure performance.
On the other hand, the “StrengthRatios” SQLite table, stores results in BLOB objects, and these cannot be visualized without specific conversion. One provides in the example, a ruby “‘final.rb” script that manipulates StrengthRatios content and performs the following operations:
Calculation of strength ratios corresponding to envelopes of load cases. This is done by calculation of maximum strength ratios for selection of load cases. Then, the envelope of strength ratios are also saved in the SQL database. Three type of envelopes are supported:
The “ENV” type of envelope calculates an envelope considering the maximum SR values for several load cases.
The “SUM” envelope calculates the summation of several envelopes. Typically the terms of this summation correspond to envelopes:
This is a first way to conservatively assess strength for a combination of different environments (thermoelastic and mechanical, for example).
When environments are not corelated, one sometimes calculates a RSS combination of results:
The post-processing provides an example of this kind of combination. The construction of envelopes is done in “final.rb” by calling method “buildSrEnvelopes”. Among other things, this method reads file “DATA/CSV_LC/EnvSum.csv” that defines, column by column, the different envelopes tha must be calculated. Figure IV.4.2 shows an example of Excel data definition.
One can also extract strength ratios, and produce Gmsh files corresponding to the different failure modes and split them according to groups corresponding to interfaces, parts... This is done by calling “outputSlpitGmsh” method in “final.rb”. This method looks as follows:
def outputSlpitGmsh(db3)
dblcCsvFiles="DATA/CSV_GMSH_SPLIT/load_cases_split_A.csv"
femsplitCsvFile="DATA/CSV_GMSH_SPLIT/SR_split_A.csv"
Manips::splitGmshFiles(db3,dblcCsvFiles,femsplitCsvFile)
end
Examples of data defining the splitting to GMSH files are shown in Figures IV.4.3 and IV.4.4. Parameter “location” in column “C” deserves additional explanation as it influences both te extraction of SR results, and the GMSH Results output.
Finally, when strength ratios have been produced by summing several envelopes, it is no longer possible to find an excel table corresponding to the critical margin of safety on a selected area in the structure. On the other hand, margin of safety can be estimated from the maximum strength ratio. “sr2xl” method performs this operation and saves the critical margins of safety in “xl_from_sr” table in SQLite database.
Several of the methods called by “final.rb” script are programmed in “Manips” module stored in “PGR/manips.rb” file. (This file has been recently displaced from “DATA" to “PGR” directory.)


| location | SQLite DB key | Result Extraction method | Gmsh output location |
| ElemCenterPoints | ElemCenterPoints | ElemCenters | ElemCenterPoints |
| Elements | Elements | ElemCorners | Elements |
| ElemStations | ElemCenterPoints | Elements | ElemNodePoints |
| NodesOnly | NodesOnly | NodesOnly | Nodes |
| Nodes | Nodes | Nodes | Nodes |
A “reportToExcelAndWord.xlsm” excel Workbook performs the final extractions to produce the final excel outputs, and the word report. This workbook contains several macros that automate the different worksheet buttons. The following operations are possible:
“extractXL” worksheet extracts results from “xl_*” tables in SQLite database and exports them to separate worksheets in a new excel workbook. “extractXL” worksheet refers to two “data” worksheets:
“extractXL_a” Worksheet defines the SQLite extraction parameters and conversion operations for each type of SQLite/excel table.
“extractXL_b” defines the list of load cases for which the extraction is done.
Data for the extraction for one selection of load cases are provided in cells C3 to C5, and the extraction is triggered by “Extract for one load case” button. The “extract for all selected load cases” button performs the extraction for several load cases using the information found on lines 11 and following.
User can copy the “extractXL” and associated Worksheets and modify the data to perform several extractions in the same Workbook.
“extractSR2XL” Worksheet extracts results from “xl_from_sr” SQLite table and saves them in different Workbooks. The data are read from cells C2 to C7, and from lines 11 and following (colmuns B, C and D). Cell C5 corresponds to the range address of conversion data in “extractSR2XL_a” Worksheet. Again, “extractSR2XL” Worksheet proposes two buttons to extract a single Workbook or all the Workbooks according to the data in lines 11 and following.
User can copy the “extractSR2XL” and associated Worksheets and modify the data to perform several extractions in the same Workbook.
The “WordTable*” Worksheets are used to copy excel tables and insert them in a Microsoft Word report.
Errors occuring during the execution of post-processing ruby scripts are often difficult to track. Generally, the exceptions raised by the different methods in the script do not convey useful information to identify the location of the error and its meaning. A majority of the errors are related to the definition of data, but one sometimes needs to go deep into the code, adding “print” statements to identify the mistake (wrong file name, reference to a non-existing group, missing parameter for an extraction of a failure criterion...).
To ease debugging, a “PrjExcept” class, deriving from ruby standard “Exception” class is defined in “PGR/prjExcept.rb” file. This class stored information related to the location of the exception, and optionnally additional information that may help to identify the source of the problem. The “dump” method of “PrjExcept” class writes to standard output stream the call stack and additional information related to an exception. For example, in “static.rb” script, one has the following code:
postList.each do |p|
begin
p.initCalcSteps()
p.calculate("Static")
rescue Exception => x
printf("Failed Post object %s with ID %s\n",p.to_s,p.postID())
PrjExcept.debug(x)
end
end
The “PrjExcept.debug(x)” inscrution calls a class method in “PrjExcept” class that write to standard output detailed information about the exception. The information corresponds to the type of exception, the location in program where exception has been raised (call stack), and additional contextual messages.
An example of output provided by the “PrjExcept.debug(x)” statement is as follows:
Exception of class PrjExcept
DUMPING exception:
PrjExcept CALL STACK (most recent call first):
1: from static.rb:53:in ‘<main>’
2: from C:/Users/ferespost/Documents/TESTSAT/RUBY/PROJECT/DATA/staticLoadCasesData.rb:251:in ‘loop’
3: from C:/Users/ferespost/Documents/TESTSAT/RUBY/PROJECT/PGR/dbAndLoadCases.rb:453:in ‘loopOnStaticCases’
4: from C:/Users/ferespost/Documents/TESTSAT/RUBY/PROJECT/PGR/dbAndLoadCases.rb:453:in ‘each’
5: from C:/Users/ferespost/Documents/TESTSAT/RUBY/PROJECT/PGR/dbAndLoadCases.rb:488:in ‘block in loopOnStaticCases’
6: from C:/Users/ferespost/Documents/TESTSAT/RUBY/PROJECT/DATA/staticLoadCasesData.rb:252:in ‘block in loop’
7: from static.rb:64:in ‘block in <main>’
8: from static.rb:64:in ‘each’
9: from static.rb:67:in ‘block (2 levels) in <main>’
10: from C:/Users/ferespost/Documents/TESTSAT/RUBY/PROJECT/PGR/post.rb:52:in ‘calculate’
11: from C:/Users/ferespost/Documents/TESTSAT/RUBY/PROJECT/PGR/postConnect.rb:269:in ‘calc_0’
12: from C:/Users/ferespost/Documents/TESTSAT/RUBY/PROJECT/PGR/postConnect.rb:249:in ‘extractConnectLoads’
PrjExcept MESSAGES:
Obtains nil resF Result for "MPCFRC"
Failed to calculate calc_0
param : interfaceDef => {"ifName"=>"pan_MX/bar_MXPY (MPCFRC)", "grpNameA"=>"pan_MX", "grpNameB"=>"bar_MXPY", "method"=>"MPCFRC"}
param : bRedistr => false
param : csId => 5
param : direction => [0.0, 0.0, 1.0]
param : type => M6
param : criteria => [["Gapping", "Gapping.gmsh", "Gapping", "xl_Gapping", {"FoS"=>1.56, "Pmin"=>7200.0, "Lg"=>0.003}], ["Sliding", "Sliding.gmsh", "Sliding", "xl_Sliding", {"FoS"=>1.25, "Pmin"=>7200.0, "Cf"=>0.25}], ["Insert", "Insert.gmsh", "Insert", "xl_Insert", {"FoS"=>1.56, "PSS"=>3300.0, "QSS"=>4500.0}]]
Sometimes an exception is not related to an error in scripts or data definition. For example, when the justification involves structure configurations in which part of the structure is missing (panel removed) the corresponding post-processing may fail and raise an exception. Then, it is advisable to comment out the call to “PrjExcept.debug(x)” in order to keep stanndard output as clean as possible:
postList.each do |p|
begin
p.initCalcSteps()
p.calculate("Static")
rescue Exception => x
printf("Failed Post object %s with ID %s\n",p.to_s,p.postID())
# PrjExcept.debug(x)
end
end
One can also decide to output debugging information only for a small selection of load cases and post-processing objects. To do this, appropriate tests must be inserted in the code above.
One can read the call stack and several messages that might help to understand the error. These messages are created in the different ruby methods where the exception is created. For example, the previous exception is created in “extractConnectLoads” of “PostConnect” class as follows:
if resF==nil then
raise PrjExcept.new(format("Obtains nil resF Result for \"%s\"",extractionMethod))
end
if resM==nil then
raise PrjExcept.new(format("Obtains nil resM Result for \"%s\"",extractionMethod))
end
The messages are added in “calc_0” method by the following instructions:
...
rescue Exception => x
x2=PrjExcept.new(x)
x2.addLine(format("Failed to redistribute connection loads"))
Util::addParamsToPrjExcept(x2," param : ",interfaceDef)
raise x2
...
A post-processing shall be run several times. In many cases, the differnt runs differ by the data of part of the post-processing. For example, one may fix errors in the connections post-processing, or test design modifications (bigger fasteners). For this example, one would advise to re-run only the post-processing of connections. This can be done by commenting out the construction of other post-processing objects. For example, in “static.rb”:
postList=[] #~ postList+=getAllStressData() #~ postList+=getSandwichData() postList+=getInterfacePostData() #~ postList+=getStaticExtractData()
this reduces somewhat the post-processing time.
But one can further reduce the post-processing by telling the “ResultsStorage” module that some of the Results must not be read from solver output files. For example:
resFilter=[] resFilter << "Grid Point Forces, MPC Forces" resFilter << "Grid Point Forces, MPC Moments" resFilter << "Displacements, Translational" resFilter << "Displacements, Rotational" ResultsStorage.setResNamesFilter(resFilter)
The last statement specifies the list of Results that are read and/or generate by linear combinations of elementary Results. In above example, the reduction of time spent on reading is generally very significant.
The post-processing object presented in this chapter is just an example of what can be done with FeResPost to manage calculations for a global project. It is improvable in many ways:
The list of extractions or failure criteria proposed in the different “Post” classes is certainly not exhaustive. Each proposed class is improvable and some failure criteria have not been proposed (calculation of bondings, of relative displacements between two parts...).
One could provide support for other types of load cases as optimizations (SOL 200), random analyses...
Presently, the project does not allow to deal with temperature fields, which might be needed for the calculation of composite failure criteria.
Project can be re-written in the language of your choice. (Python for example.)
...
FeResPost is also distributed as a Python compiled library.
In general, the class names, their methods and attributes (properties), the parameters of these methods and attributes are the same as those available in the FeResPost ruby extension. The user is referred to Parts I, II, III and IV to find information on the use of the different classes and methods. In most cases, the information given there is sufficient to use the Python extension.
Typically, one imports the FeResPost Classes and Modules with a statement as:
from FeResPost import *
Note however that it works only if the different environment variables have been initialized correctly. Typically, in our Windows examples, this is done through the batch files that are used to launch the example scripts, and the following variables are generally initialized:
set LIB= set INCLUDE= set PYTHONPATH=C:/Users/ferespost/Documents/SRC/OUTPUTS/PYTHON/PYTHON_35 set PYTHONINSTALLDIR=C:/NewProgs/PYTHON/PYTHON_35 set REDISTRPATH=C:/Users/ferespost/Documents/SRC/OUTPUTS/REDISTR set PATH=%PYTHONINSTALLDIR%;%REDISTRPATH%;C:/Windows/System32
Of course the different paths you will initialize will have to be adapted to you peculiar installation, and to the version of Python you are using. See the description of ruby examples in chapter IV.0 for more explanations on the “PATH” variable definition.
Most of the differences of FeResPost Python and ruby libraries are directly related to the differences of the two languages, which are very similar as far as the different language concepts are concerned. Therefore, the adaptation of ruby examples to Python language should not be very difficult.
One highlights below some differences between Python and ruby extensions that are related to specific programmatic aspects of the two different systems.
New instances of the FeResPost classes are obtained by calling the corresponding class constructor:
... from FeResPost import * ... db=NastranDb() ...
The Python “list” object corresponds to ruby “Array”, and the Python ”Dictionary” corresponds to ruby “Hash” objects. One remarks however that the Python dictionary keys cannot be “list” objects. When this problem occurs, the ruby Array should be converted in a Python tuple instead of a Python list. (See for example the example “PYTHON/EX23/testHDF.py” in section V.1.2.)
It is not possible to define several iterators in a given class in Python. Therefore, several special “Iterator” classes have been created in Python library. They are returned by the different FeResPost classes as is done for the COM component.
Let us illustrate it by an example... Consider the “each_ply” iterator defined in ClaLam class of FeResPost ruby extension. With the ruby extension, the iteration on the plies of a laminate may be performed as follows:
... lam.each_ply do |plyDescr| ... end ...
With Python, the code becomes:
... for ply in lam.iter_ply(): ... ...
One could also write:
... x=lam.iter_ply() for ply in x: ... ...
As in the FeResPost ruby extension, each iterator method name starts with “each_”, correspondingly, the Python methods returning an Iterator object have a name that starts with “iter_”. The correspondence between ruby extension methods and COM component methods is obvious: “each_ply” becomes “iter_ply”, “each_material” becomes “iter_material”,...
With FeResPost ruby extension, an optional argument can be set to “nil” when not provided. The “nil” argument is to be replaced by “None” value in Python.
Python exceptions are managed as ruby exceptions. Only the message associated to standard exceptions is printed differently:
try:
db.readBdf("unit_xyz_V1.bdf",["../../MODEL/MESH/"],"bdf",{},True)
except BaseException as x :
print("\n\nMaybe you should modify the two first include statements in main file!")
print("**********************************************************************\n")
print("Got exception with following message:\n")
print(str(x))
As the adaptation from ruby to Python is straightforward, the current chapter is also very short. We only highlight some of the differences related to ruby and Python language differences.
An example of an iterator with Python library is in “PYTHON/EX02/printGroups.py” and reads as follows:
for groupName in db.iter_groupName():
grp = db.getGroupCopy(groupName)
nodesNbr = grp.NbrElements
elementsNbr = grp.NbrNodes
rbesNbr = grp.NbrRbes
coordNbr = grp.NbrCoordSys
print("%20s%10d%10d%10d%10d"%(groupName,nodesNbr,elementsNbr,
rbesNbr,coordNbr))
Note:
The parentheses at the end of “iter_groupName” method call. (This is specific to the Python language.)
The “:” that defines the beginning of the instructionqs bloc in Python. This is also specific to Python language, as is the fact that the indentation of the code defines the limits of instruction blocs.
And of course, the fact that ruby “each_groupName” iteration method is replaced by a call to the Python “iter_groupName” function that returns an iterable object.
An example of reading HDF Results with Python library is given in “PYTHON/EX23/testHDF.py” and corresponds to the ruby example described in section IV.2.9. The part related to HDF access looks as follows:
Post.loadHdf5Library("C:/NewProgs/HDF5/HDF5-1.8.20-win32/bin/hdf5.dll")
...
db.attachHdf(hdfName)
lcNames=db.getHdfAttachmentLcNames(hdfName)
lcName=lcNames[lcIndex]
scNames=db.getHdfAttachmentScNames(hdfName,lcName)
scName=scNames[scIndex]
resNames=db.getHdfAttachmentResNames(hdfName,lcName)
hdfResNames=list(resNames)
db.readHdfAttachmentResults(hdfName,lcName,scName,resNames)
...
Note that the example also outputs Results read from an XDB file:
...
results=db.getAttachmentResults(xdbName,lcName,scName,hdfResNames)
...
for tpName in hdfResNames:
print lcName,scName,tpName
resKey=tuple((lcName,scName,tpName))
tmpRes=None
if resKey in results.keys():
tmpRes=results[resKey]
if (tmpRes):
os.write("%-20s%-25s%-60s%-10d\n"%(lcName,scName,tpName,tmpRes.Size))
os.write("%10d%10d%14g%14g : %s\n"%(tmpRes.getIntId(0),tmpRes.getIntId(1),tmpRes.getRealId(0),tmpRes.getRealId(1),tmpRes.Name))
Util.printRes(os,tmpRes.Name,tmpRes)
else:
print lcName,scName,tpName
...
(Remark that the access to “results” dictionnary elements is done via “resKey” tuple.)
The use of SQLite library is explained in Python documentation. With FeResPost, the BLOB object returned by “toBlob” method must be converted into a Python buffer using the corresponding function:
for lcName in lcNames: for resName in resNames: results=db.getAttachmentResults(xdbFileName,lcName,scNames,resName) if (results): for key,res in results.iteritems(): print key sqldb.execute( "insert or replace into dynam_results_1 values(?,?,?,?,?,?,?,?,?,?)", [lcName,key[1],resName,res.TensorOrder, res.getIntId(0),res.getIntId(1), res.getRealId(0),res.getRealId(1), res.Size,buffer(res.toBlob())]) sqldb.commit() else: print "NO FOR" + lcName + resName
Note that the call to “buffer” method seems necessary with versions 2.* of Python, but must be removed for version 3.*.
In directory “TESTSAT/PYTHON/PROJECTb” one presents an object-oriented post-processing. This project is the translation of the corresponding ruby example presented in chapter X.E.4.
Significant differences in the programming of the two projects deserve to be noted:
It seems Python does not allow to define object methods. Therefore, for each object in the ruby project that defines its own methods, one must define an additional class in the Python project.
For example, the ruby project defines an instance of the “PostCauchy” class called “post_honeycomb”, and the “post_honeycomb” object defines post-processing data in the instance methods. With Python, one first defines a “PostHoneycomb” class that defines the methods used to fill post-processing data. this means that one msut define an additional class.
In ruby “LoadCases” module, several “proc” objects have been defined. In Python corresponding module, one defines methods corresponding to the “procs”, because the equivalent of ruby proc does not seem to exist in Python. (Python “lambdas” only allow the definition of simple expressions.)
The Python examples in directory “TESTSAT/PYTHON/EX27” are a simple translation of the ruby example discussed in section IV.2.11.
On Windows OS, FeResPost is distributed at the same time as a ruby extension, and as a COM component. One describes in this Part several characteristics of FeResPost as a COM component.
In general, the class names, their methods and attributes (properties), the parameters of these methods and attributes are the same as those available in the FeResPost ruby extension. When necessary, modifications have been done in the ruby extension in order to maintain as much as possible the compatibility between the ruby extension and the COM component. Therefore, the user is referred to Parts I, II, III and IV to find information on the use of the different classes and methods. In most cases, the information given there is sufficient to use the COM component.
However, an exact match between the ruby extension and COM component is not possible. One details below the conventions that have been adopted when incompatibility problems were not solved. More generally, one explains here the specific aspects of the use of FeResPost as a COM component.
This Part of the document is organized as follows:
Chapter VI.2 presents the COM characteristics of the FeResPost generic classes described in Part I.
Chapter VI.1 presents the COM characteristics of the FeResPost CLA classes described in Part II.
Chapter VI.3 presents the COM characteristics of the FeResPost generic classes described in Part III. (Solver classes.)
In Chapter VII.1, one gives a few examples illustrating the use of FeResPost COM component.
The present Chapter discusses the following points:
The different ways to access the COM component depending on the language and/or on the programming environment (section VI.0.1).
In section VI.0.2, one describes conventions that have been adopted when translating the ruby extension into a COM component. Information is given each time the ruby methods are modified to be implemented into the COM component. For example, this is done for iterators, operators, “clone” method... Also one explains how objects are created with the component.
The installation (registration) of the COM component is described in section X.A.4.5).
One makes the distinction between the different programming languages and programming environments. The access to the component is always done by a request of the kind
‘‘create object’’ FeResPost_3_4_4.Application
in which the three integers correspond to the version of FeResPost. (Several versions of FeResPost can be installed simultaneously on a computer.) One intends to maintain the same conventions for the naming of the FeResPost COM component.
When the application is started, the corresponding window appears. This window can be made visible or invisible by setting the “Visible” property of the application object to True or False respectively. The window presents for each class a count of the number of objects available in the memory, and of the number of references to these objects. Note that when the property is set to True, the execution of the program might slow down significantly. Therefore, the property should be set to True for debugging only.
Even though FeResPost is first programmed as a ruby extension, the COM component can also be accessed from ruby language. For this, one first requires the “win32ole” ruby extension that allows the access to all the COM components installed on the computer. Then the FeResPost component can be accesses by requiring the corresponding application:
require ’win32ole’
...
frpApp = WIN32OLE.new("FeResPost_3_4_4.Application")
In the example, above one required the 3.4.4 version of the FeResPost COM component, and stores a reference to this application in “frpApp” variable.
Note that memory leakage has been observed in win32ole extension of ruby language. This can result in COM objects not being released when they should be. This bug, not related to FeResPost, is currently under investigation, and should be fixed in version 1.8.7 of ruby.
The access to the FeResPost COM component from python is similar to the access from ruby. A win32con extension must first be imported, then the component can be accessed:
import win32con
from win32com.client import Dispatch, constants
...
frpApp = Dispatch("FeResPost_3_4_4.Application")
In this case, no special extension is required because the OLE support is “build-in” the language. The application is simply accessed with the following statement:
set frpApp= CreateObject("FeResPost_3_4_4.Application")
When programming in VBA, for example in excel, the component must first be referenced in the excel workbook. For this:
Open the VBA editor from an excel workbook.
Go to the “Tools” menu and select the “References” menu.
There, you select the (or one of the) available FeResPost library. For example, for version 3.1.7, the library is referred to as “FeResPost 3.1.7 COM server”.
Quit the “Tools/References” menu.
Then, the server can be accessed from excel VBA code with a statement like:
set frpApp= CreateObject("FeResPost_3_1_7.Application")
Once the FeResPost component library is activated, the different classes and the corresponding methods can be viewed in the object explorer. During the VBA program execution, the behavior of the different classes and methods can also be watched.
If you want to change the version of VBA used in an existing excel VBA project, proceed as follows:
It may be practical to un-activate the execution of excel VBA macros before doing the following operations.
Make sure that the new version of FeResPost is properly registered.
Open the VBA editor from an excel workbook.
Go to the “Tools” menu and select the “References” menu.
Un-select the old version of FeResPost COM server. (The one you no longer want to use.)
Quit the “Tools/References” menu.
Re-enter into the “Tools” menu and select the “References” menu.
Select the new version of FeResPost COM server you want to use in the workbook.
Quit the “Tools/References” menu.
Do not forget to modify the version of the server requested by “CreateObject” method in excel VBA code.
If you no longer need the old version of FeResPost COM server, you can un-register it and delete the corresponding files from your computer.
Section VII.1.1.4 shows an example of C++ program in which the component is accessed. This object shows that the use of COM component from compiled languages is significantly more difficult than from interpreted languages. This is related to the fact that the management of many operations has to be done by the programmer and is no longer dealt with by the interpreted language.
This example also shows that additional information should be added to the documentation to allow an easy access to the different methods and classes of the component by the compiled languages programmers. This documentation is still under development.
Actually, the example shows even more that the component that is being developed is adapted to the use with languages that support the Microsoft IDispatch interface. However, a library adapted to the use with C++ language should also be developed. Consequently we do not advise to use the component from C++ or C language.
One highlights below some differences between COM component and ruby extension that are related to specific programmatic aspects of the two different systems.
New instances of the FeResPost classes are obtained by calling the “newObject” method of FeResPost application. The argument of this method is a String containing the name of the class of which a new object is requested. For example, in ruby, the creation of new instances is done with statements like:
...
frpApp = WIN32OLE.new("FeResPost_3_4_4.Application")
...
db=frpApp.newObject("ClaDb")
...
mat=frpApp.newObject("ClaMat")
...
The corresponding VBscript lines of code follow:
...
set frpApp= CreateObject("FeResPost_3_4_4.Application")
...
set db=frpApp.newObject("ClaDb")
...
set mat=frpApp.newObject("ClaMat")
...
By default, COM does not define associative containers (i.e. containers that associate keys and values, like the “Hash” class of ruby language.) As in FeResPost ruby extension, Hash objects are often used as method arguments, or values returned by these methods, A convention must be agreed upon to determine the type of arguments that are to be used to replace these Hashes.
The convention that has been adopted is that each Hash is replaced by a 2D Array:
The first index range for this array corresponds to the number of key-value pairs of the corresponding Hash argument.
The second index ranges from 0 to 1 (two values). The value 0 corresponds to the key and the value 1 corresponds to the value of the pair.
One notes that the indices used to access the elements of an Array start with 0 corresponding to the first element. This is a convention that has systematically been used for all the Array produced by FeResPost COM component. This convention is that same as the one of FeResPost ruby extension, and is consistent with C, C++, ruby and many other programming languages.
COM provides a standard interface that allows the writing of iterators on collections of different types. In FeResPost, the iteration is based on the IEnumVARIANT interface. One notes however, that it does not seem possible to implement a class that defines several enumerators. This is why, an additional class corresponding to the iteration has been created in FeResPost: the “Iterator” class.
The “Iterator” class is common to all the iterators of all the FeResPost classes. But an Iterator object behaves differently depending on the class that produces it and/or the method of the class that is used to produce it.
Let us illustrate it by an example... Consider the “each_ply” iterator defined in ClaLam class of FeResPost ruby extension. With the ruby extension, the iteration on the plies of a laminate may be performed as follows:
... lam.each_ply do |plyDescr| ... end ...
With FeResPost COM component, an Iterator must first be produced before iterating on the elements of the corresponding collection. This can be done as follows:
... plyIt = lam.iter_ply plyIt.each do |plyDescr| ... end ...
This examples illustrates the conventions that have been used when programming the FeResPost COM component to transpose the iterators proposed in the ruby extension:
As in the FeResPost ruby extension, each iterator method name starts with “each_”, correspondingly, the COM component methods returning an Iterator object have a name that starts with “iter_”. The correspondence between ruby extension methods and COM component methods is obvious: “each_ply” becomes “iter_ply”, “each_material” becomes “iter_material”,...
When the COM iteration method has no argument, it is a property “getter” that is used instead of a method. Otherwise, a method with argument is defined.
In ruby using the COM component, the iteration on the Iterator object is done using “each” iteration method.
Note that to the ruby lines given as example above, one prefers the shorter notation:
... lam.iter_ply.each do |plyDescr| ... end ...
The corresponding code in python may be:
... for plyDescr in lam.iter_ply: ... ...
and in VBscript, one shall have:
... for each plyDescr in lam.iter_ply ... Next ...
Operators are unsupported in COM. Therefore, the operators that are defined by ruby classes are replaced by methods in COM component:
Method “opAdd” corresponds to operator “+”,
Method “opSub” corresponds to operator “-”,
Method “opMul” corresponds to operator “*”,
Method “opDiv” corresponds to operator “/”,
Method “opPow” corresponds to operator “**” (power).
For example, the following ruby statement:
z=x+y
becomes, with COM component:
z=x.opAdd(y)
Note that the different “operator” methods defined in ruby “Post” module are also defined in the “Application” class of COM component (section VI.2.1).
In ruby language, classes may define singleton methods that can be called directly from the class, and not from an instance of the class. Apparently, this capability is unsupported by COM classes.
Therefore, all the singleton methods defined in ruby extension are defined as instance methods in COM component. This means that before using such a method, an instance of the corresponding class must be defined first.
When one class of the ruby extension defines a “clone” method, the corresponding method of the COM component defines a “makeCopy” method. This has been done to avoid method name conflicts when the COM component is used with ruby language.
In ruby extension, several methods are defined in “Post” Module. In COM component, these methods are defined in “Application” class.
In ruby extension, several methods have complex arguments. No standard “Complex” class exists in COM, even though the “Complex” class is available in most programming languages. In FeResPost COM component one decided that the convention is to represent Complex numbers by Arrays of two real numbers corresponding to the real and imaginary parts of the number.
With FeResPost ruby extension, an optional argument can be set to “nil” when not provided. The “nil” argument also works when the COM component is used with ruby language. in VBA, the “nil” argument can be replaced by an unitialized Variant object (VT_EMPTY variant type).
It is not possible to associate an error message to errors returned by COM component. But method “getLastErrorMessage” defined in FeResPost Application class allows to obtain the message associated to the last exception raised by FeResPost. This method can be used to retrieve and print the message. Here is a ruby example of exception management with COM component:
begin
db.readBdf("unit_xyz_V1.bdf",["../../MODEL/MESH/"],"bdf",nil,true)
rescue Exception => x then
printf("\n\nMaybe you should modify the two first include statements in main file!\n")
printf("**********************************************************************\n\n")
puts frpApp.getLastErrorMessage()
end
In general, the selection of output stream for the writing of FeResPost information messages follows the same rules as for ruby extension, as explained in section I.6.1. However, it is not possible to set FeResPost information output stream to COM client’s output streams. This is related to the fact that the type of output stream depends on the client language (ruby, python, VBA, C++...). This has two consequences:
The equivalent to method “setInfoStreamToClientStream” does not exist in COM component.
COM component default information stream is set to C++ std::cout output stream, and not to the client’s language standard output stream.
The different classes described in this Chapter correspond to the classes described in Part II. The methods defined in FeResPost COM component CLA classes are the same as those defined in the FeResPost ruby extension CLA classes, except the peculiar problem of the iterators discussed in section VI.0.2.3, and of the “clone” methods that have been replaced by “makeCopy” methods.
Similarly, the arguments defined for the different methods of CLA classes are the same as those for the classes of FeResPost ruby extension, except for the remark done in section VI.0.2.2 for the “Hash” arguments or returned values.
In the rest of this Chapter, one makes a few remarks about the different classes. But otherwise, the reader is referred to the different chapters of Part II to find information on the use of COM component CLA classes.
This class corresponds to “IClaDb” interface. No peculiar remark is to be done except for the iterators:
Iterator “each_material” in ruby extension becomes “iter_material”.
Iterator “each_materialId” in ruby extension becomes “iter_materialId”.
Iterator “each_laminate” in ruby extension becomes “iter_laminate”.
Iterator “each_laminateId” in ruby extension becomes “iter_laminteId”.
Iterator “each_load” in ruby extension becomes “iter_load”.
Iterator “each_loadId” in ruby extension becomes “iter_loadId”.
The “makeCopy” method that returns a copy of the object.
This class corresponds to “IClaMat” interface.
Methods returning a 2D matrix, return a an Array with 2 dimensions. These methods are “getCompliance”, “getStiffness”, “getInPlaneCompliance”, “getInPlaneStiffness”, “getOOPSCompliance”, “getOOPSStiffness”, “getInPlaneLambdaT”, “getInPlaneLambdaH”. (In ruby extension, these methods return an array of arrays.)
The “makeCopy” method that returns a copy of the object.
This class corresponds to “IClaLam” interface.
Methods returning a 2D matrix, return a an Array with 2 dimensions. These methods are “get_ABBD”, “get_G”, “get_abbd_complMat”, “get_g_complMat”, “get_LambdaT”, “get_LambdaH”. (In ruby extension, these methods return an array of arrays.)
Methods that return Ply stresses, strains, temperature or moisture return 2D Arrays of size N*8 or N*3.
The “getDerived”, “getFailureIndices” and “getReserveFactors” methods return Arrays of 2 objects. The second object is a 2D Array in COM component.
Methods “getMaxDerived”, “getMinDerived”, “getMaxFailureIndices”, “getMinFailureIndices”, “getMaxReserveFactors” and “getMinReserveFactors” returns 2 dimensional Arrays of sizes N*3.
Iterator “each_ply” in ruby extension becomes “iter_ply”.
The “makeCopy” method that returns a copy of the object.
This class corresponds to “IClaLoad” interface. No peculiar remark is to be done. The “makeCopy” method that returns a copy of the object.
Most classes defined in this chapter correspond to the same classes in ruby extension.
One class correspond to modules in ruby extension: the “Application” class described in section VI.2.1 corresponds more or less to the “FeResPost” module in ruby extension, even though its purpose is not exactly the same. This class also inherits the methods defined in “Post” module of ruby extension.
The two classes “Iterator” and “IterX” correspond to the iterators defined in the different classes of the COM component. These classes are not described in this chapter. Indeed, one considers that the explanations given in section VI.0.2.3 about the use of iterators is sufficient. Of course no corresponding class exists in the ruby extension.
This class corresponds to the “IApplication” interface. Only one object of the class Application can be created, even though several references to this object can be used in a program.
The “Visible” property can either be set or got. The value of this property specifies whether the Application main window is visible or not. The Application main window shows the number of FeResPost COM objects that have been created and the number of references to these object. This information is provided by class, and one also gives the summary for all classes in last “TOTAL” line.
Note that it is not because an Application is not “Visible” that it is not running.
The method “newObject” is used to create objects for the different classes of the COM component. Its argument is a String corresponding to the name of the class for which an object is requested. The created object is the return value. For example, when the following statement is used:
db=frpApp.newObject("NastranDb")
creates a new Nastran DataBase object and a reference is stored in “db” variable.
All the methods which in ruby extension are defined in “Post” module, are defined in “Application” class for the COM component. Presently, these methods are
The methods “openMsgOutputFile”, “closeMsgOutputFile” and “writeAboutInformation”.
The methods “readGroupsFromPatranSession” and “writeGroupsToPatranSession” to read lists of Groups in Arrays.
Several methods for the manipulation of Results like “cmp”, “max”, “sin”, “sq”, “exp”,...
Dyadic “operators” on Results like “opAdd”, “opMul”,...
The “convertBlob” method deals with Array of Bytes (unsigned char) instead of Strings in the ruby extension.
...
When working with “FeResPost.exe” out-of-proc solver, also called “local server” it may be interesting to change the working directory of the server, to match the one of the client, for example. Two methods have been added to the COM component:
“setCurrentDirectory” has one string argument and sets the server current, or working directory.
“getCurrentDirectory” has no argument and returns a string corresponding to the server current working directory.
These two methods are specific to the COM component. They are not defined in the .NET assembly, or the ruby extension.
For “in-proc” server (or dll server), these two methods have no effect.
This class corresponds to the generic DataBase class of ruby described in Chapter I.1. The class cannot be instantiated; only the interface “IDataBase” has been defined. The DataBase classes corresponding to the different solvers derive from the “IDataBase” interface.
The iterators of the DataBase class in ruby extension have also been defined in COM
component: “iter_abbreviation”, “iter_groupName”, “iter_resultKey”, “iter_resultKeyCaseId”,
“iter_resultKeySubCaseId”, “iter_resultKeyLcScId” and ‘iter_resultKeyResId” properties in COM
component correspond to the “each_abbreviation”, “each_groupName”, “each_resultKey”,
“each_resultKeyCaseId”, “each_resultKeySubCaseId”, “each_resultKeyLcScId” and
“each_resultKeyResId” iterators in ruby extension.
The four singleton methods “enableLayeredResultsReading”, “disableLayeredResultsReading”, “enableSubLayersReading” and “disableSubLayersReading” in the ruby extension generic DataBase class are defined as instance methods. This means that an instance of the derived class must be created to use these singleton methods.
The same is true for methods “setStorageBufferMaxCapacity” and “getStorageBufferMaxCapacity”.
Most methods of the “Group” class are exactly the same as the ones defined in the Group class of ruby extension (Chapter I.3). Several methods or properties are different however:
The iterators are now “iter_element”, “iter_rbe”, “iter_node” and “iter_coordsys” instead of “each_element”, “each_rbe”, “each_node” and “each_coordsys”.
The four operators “+”, “-”, “*” and “/” are replaced by the methods “opAdd”, “opSub”, “opMul” and “opDiv” respectively.
The “toBlob” and “fromBlob” methods deal with Array of Bytes (unsigned char) instead of Strings in the ruby extension.
The “makeCopy” method that returns a copy of the object.
Methods of the “CoordSys” class are the same as the ones defined in the CoordSys class in ruby extension. The “makeCopy” method that returns a copy of the object.
Most methods of the “Result” class are exactly the same as the ones defined in the Result class in ruby extension (Chapter I.4). Several methods or properties are different however:
The iterators are now “iter”, “iter_key” and “iter_values”.
The five operators “+”, “-”, “*”, “/” and “**” are replaced by the methods “opAdd”, “opSub”, “opMul”, “opDiv” and “opPow” respectively.
The “getData” method returns a 2D Array, instead of an array of arrays in the ruby extension.
The “toBlob” and “fromBlob” methods deal with Array of Bytes (unsigned char) instead of Strings in the ruby extension.
The “makeCopy” method that returns a copy of the object.
Methods of the “ResKeyList” class are the same as the ones defined in the ResKeyList class in ruby extension. Only the single iterator is different: However:
The property “each_key” is here named “iter_key”.
The “getData” method returns a 2D Array, instead of an array of arrays as in the ruby extension.
The “makeCopy” method returns a copy of the object.
The two classes that correspond to the two supported solvers (Nastran and Samcef) are complete.
The “NastranDb” class stores a model and results corresponds to Nastran finite element solver. It corresponds to “INastranDb” interface that derives from the “IDataBase” interface described in section VI.2.2. Methods specific to the COM component are:
The “makeCopy” method that returns a copy of the dataBase.
Several iterator methods with or without argument: “iter_coordSysId”, “iter_elemId”, “iter_nodeId”, “iter_rbeId”, “iter_materialId”, “iter_propertyId”, “iter_nodeOfElement”, “iter_cornerNodeOfElement”. When these iterators have arguments, they are implemented with methods and not with properties.
The reader is referred to Chapter III.1 for the description of the other methods.
The “SamcefDb” class stores a model and results corresponds to Samcef finite element solver. It corresponds to “ISamcefDb” interface that derives from the “IDataBase” interface described in section VI.2.2. The other methods that are available are:
The “makeCopy” method that returns a copy of the dataBase.
Several iterator methods with or without argument: “iter_coordSysId”, “iter_elemId”,
“iter_nodeId”, “iter_materialId”, “iter_samcefPlyId”, “iter_samcefLaminateId”,
“iter_samcefMatIdName”, “iter_samcefMatNameId”, “iter_nodeOfElement”,
“iter_cornerNodeOfElement”. When these iterators have arguments, they are
implemented with methods and not with properties.
The reader is referred to Chapter III.2 for the description of the other methods.
COM examples can be run on Windows only. Therefore, these examples should be launched via batch scripts that define the environment variables needed for the execution. For example, in directory “COMEX/EX03”, one enters the command:
exec ruby -I. makeGravForces.rb
or
exec python printstressmax.py
The “exec.bat” script contains, for example, the following lines:
setlocal call "../ENV/env.bat" echo %PATH% %* endlocal
in which the environment defines the variables specifying the version of python or ruby to be used, and the PATH to the directories containing executable and libraries used for the executation. For example:
set WINLIBS=C:/Users/ferespost/Documents/SRC/OUTPUTS/REDISTR;C:/Windows/System32 set PATH=C:/NewProgs/PYTHON/PYTHON_37;C:/NEWPROGS/RUBY/ruby-2.5.1-1-x86/bin;%WINLIBS% set PYTHONPATH=C:/Users/ferespost/Documents/SRC/OUTPUTS/PYTHON/PYTHON_37
The launch of excel examples is slightly different. For example, the script launching the classical laminate analysis with excel in directory “EX06” contains:
setlocal call "../ENV/env.bat" LaminateAnalysis.xls endlocal
In this Chapter one shows examples illustrating the use of the COM component with interpreted or compiled languages. All the examples can work only if the COM component has been properly installed as explained in section X.A.4.5. Note also, that the examples presented below assume that you have installed version 3.4.0 of the FeResPost COM component. If another version is installed, some lines in the program must be adapted.
In this section, one presents an example in which the FeResPost COM component is used to automate CLA analyses with different programming languages. The same calculations are done with different programming languages. This allows the user to identify the similarities and differences of FeResPost COM automation with different programming languages:
The most detailed example is given in section VII.1.1.1 where a python program calculates and prints laminate properties and load responses. (In the other examples, one only presents the aspects of programming peculiar to the language.)
In section VII.1.1.2, the ruby version of the program is given.
The VBscript version is given in section VII.1.1.3. (Even though you will see that there is a problem in this example.)
In section VII.1.1.4, one programs the example in C++. This requires a compilation of the example.
Section VII.1.1.5 was added to allow the presentation of an automation program in C. This has not been one yet, however.
The file “COMEX/EX01/testClaCom.py” contains the python program lines for automation of CLA calculations with python. One gives below some explanation about how the program works.
First, some python standard packages must be imported to allow the OLE automation to be used in the program. Therefore, the following statements are added at the beginning of the program:
import sys import win32con from win32com.client import Dispatch, constants
Then the program defines several methods that are used in the main program:
The method “id2str” converts an idfier returned by one CLA method into a string that can be used when results are printed. Remember that a CLA idfier is either an integer, a String or an Array containing one integer and one String. The method “id2str” tests the type of the “id” argument and performs the necessary operations to convert it to a String.
The method “printLamProperties” writes a laminate definition and several of its properties (ABBD matrix, G matrix, CTE vectors...). The method has three arguments:
“db”: a ClaDb object (composite dataBase). The laminate shall be retrieved from this dataBase.
“os”: the output stream in which results are written.
“lamID”: an idfier corresponding to the ClaLam object for which properties are written.
The lamID argument is used to obtain a copy of the laminate from the dataBase. Then, the definition and the properties are written in the output stream. The programming lines that perform these operations are easy to understand and require no additional explanation.
The method “printLoadResponse” calculates the laminate load response for a selected loading. The method has six arguments:
“db”: a ClaDb object (composite dataBase). The laminate and the load used in calculations shall be retrieved from this dataBase.
“os”: the output stream in which results are written.
“lamID”: an idfier corresponding to the ClaLam object for which load response is calculated.
“loadID”: an idfier corresponding to the ClaLoad object for which load response is calculated.
“theta”: a real argument corresponding to the angles of load applied to laminate wrt laminate axes.
“criteria”: an Array of Strings corresponding to the list of criteria for which reserve factors are calculated.
At the beginning of the method, the ClaLam and ClaLoad objects are retrieved from the dataBase and the laminate load response is calculated as follows:
lam=db.getLaminateCopy(lamID)
load=db.getLoadCopy(loadID)
lam.calcResponse(db,theta,load,True,True,True)
(Note that the ply result calculation is requested at bottom, mid and upper layers of each ply.) Then several results are extracted from the ClaLam object and printed in output stream:
The laminate normal forces, bending moments, normal strains and curvatures, in laminate axes.
The ply stresses in ply axes.
The ply strains in ply axes.
The reserve factors for the selected criteria. These reserve factors are calculated with a unit safety factor.
Note that other results could be calculated as failure indices. This is left as an exercise. Note also that the interpretation of ply results requires some understanding of the structure of results returned by methods like “getPliesStresses”, “getPliesStrains”, “getReserveFactors”... The information provided in Part II of this manual and in Chapter VI.0 should be sufficient, even though it requires to spend some time on the analysis of the example.
No “main” function is defined in the program. Instead, the last lines of the program file contain the instructions that perform the main analysis.
First the component must be accessed and a ClaDb object created and initialized. This is done as follows:
frpApp = Dispatch("FeResPost_3_4_0.Application")
db=frpApp.newObject("ClaDb")
db.readNeutral("test.ndf")
Note that the access to the application requires the full name of the application that includes the version identification. This means that the name will have to be changed if another version of the component is used. The initialization of the ClaDb object involves the reading of “test.ndf” neutral data file.
The output of the results is done in a disk file:
os=file("testClaCom_py.txt","w")
Note that the use of iterators with python is easy. For those who know python, to understand the following lines should not be a problem:
for lamId in db.iter_laminateId: printLamProperties(db,os,lamId) for loadId in db.iter_loadId: printLoadResponse(db,os,lamId,loadId,0.0,criteria)
One first makes a loop on the laminates and prints their properties. Then, inside the loop on the laminates, a loop on the loads stored in the dataBase is done and the laminate load response is calculated and printed. The criteria that are calculated are: “TsaiHill”, “Ilss” and “YamadaSun”.
When the program is run, the FeResPost component application window exhibits the number of component objects referenced, and the number of references. You may stop the program at several locations to check this information. (By adding windows message boxes for example.)
The file “COMEX/EX01/testClaCom.rb” contains the ruby program lines for automation of CLA calculations with ruby. The ruby program is very similar to the python program:
At the beginning, one needs to load several standard packages:
require ’Win32API’
require ’win32ole’
“Win32API” is necessary to create message box windows. “win32ole” is necessary for the OLE automation.
the program defines the same three methods as python program in section VII.1.1.1: “id2str”, “printLamProperties” and “printLoadResponse”. These methods are nearly the exact equivalent as the same methods in the python version of the program.
In the main program, the access to the COM component, and the creation of the ClaDb dataBase are done as follows:
frpApp = WIN32OLE.new("FeResPost_3_4_0.Application")
db=frpApp.newObject("ClaDb")
db.readNeutral("test.ndf")
(Here again, you may have to change the version number of FeResPost to match the version installed on your computer.) The loop on laminate and load IDs looks as follows:
db.iter_laminateId.each do |lamId|
printLamProperties(db,os,lamId)
db.iter_loadId.each do |loadId|
printLoadResponse(db,os,lamId,loadId,0.0,criteria)
end
end
Note that the window created at the end of the program may show that some of the references to COM objects have not been released. Then this is a problem in “win32ole”extension of ruby, but not in FeResPost COM component.
The file “COMEX/EX01/testClaCom.vbs” contains the VBscript program lines for automation of CLA calculations with VBscript. The VBscript version of the example is rather short, and it does not work: there is a problem with the access to elements of 2D matrices. If someone can explain us what is wrong, we would appreciate.
We just show below how the component is accessed, and the ClaDb object initialized:
set frpApp= CreateObject("FeResPost_3_4_0.Application")
set db=frpApp.newObject("ClaDb")
db.readNeutral "test.ndf"
The example is provided in the following files:
“COMEX/EX01/testClaCom.cpp” is the principal file containing calculation functions and the main program.
“COMEX/EX01/util.cpp” contains the definition of utility functions. (Mainly conversion functions.)
“COMEX/EX01/util.h” contains the declarations of the same functions.
The batch file “COMEX/EX01/build.bat” is used to compile the example. The compilation messages should look as follows:
g++ -c testClaCom.cpp -I"H:\OUTPUTS\COM\include" g++ -c util.cpp g++ -o testClaCom.exe testClaCom.o util.o \ "H:\OUTPUTS\COM\lib\FeresPost.dll" -lole32 -loleaut32 \ -luuid -lstdc++
(You may have to change the compilation commands, options and files access to compile the program on your computer.)
In a C++ program, several headers must first be included in the program to have access to classes, methods and GUIDs declarations and/or definitions:
#include <Application.hxx> #include <Application_i.c> #include <ClaDb.hxx> #include <ClaLam.hxx> #include <ClaMat.hxx> #include <ClaLoad.hxx> #include <IterX.hxx> #include <Iterator.hxx>
(The included files are distributed with the FeResPost COM library in the “include” directory.) The access to the component and the initialization is done as follow:
if (!CoInitialize(0)){
if ((hr = CoGetClassObject(CLSID_Application, CLSCTX_INPROC_SERVER,
0, IID_IClassFactory, (LPVOID *)&classFactory))) {
MessageBox(0, "Can’t get IClassFactory", "CoGetClassObject error",
MB_OK|MB_ICONEXCLAMATION);
cerr << hr << endl ;
exit(-1);
}
else {
if ((hr = classFactory->CreateInstance(0, IID_IApplication,
(LPVOID *)&frpApp))) {
classFactory->Release();
MessageBox(0, "Can’t create IApplication object",
"CreateInstance error",MB_OK|MB_ICONEXCLAMATION);
return -1;
}
else {
classFactory->Release();
MessageBox(0, "SUCCESS", "SUCCESS", MB_OK|MB_ICONEXCLAMATION);
}
}
}
frpApp->newObject(BSTR_ClaDb,(IDispatch**)&db);
string2variant("test.ndf",fileName);
db->readNeutral(fileName);
As you can see, it is a little more complicated than in ruby or python.
The entire C++ example shows that it is significantly more complicated to use COM component with compiled languages than with interpreted languages that support COM automation. This is related to several factors:
The scanning of results returned by FeResPost methods is generally more complex than with an interpreted language because all the conversion operations must be done “manually” by the programmer.
The development of a set of functions performing the conversions may reduce slightly the burden of programming these operations. However, it shall always be significantly more tedious in C++ than in python or ruby.
Similarly, when methods have a variable number of arguments, these are passed by a SafeArray that has to be prepared before calling the method.
All the conversions to or from VARIANT variables must be managed by the programmer, while interpreted languages manage most of this job.
The programmer cannot forget to call the “Release” method when appropriate to avoid memory leakage.
...
Just to illustrate the points above, one gives below an example of the programming lines necessary to perform the iterations on laminate and load IDs and call the calculation functions:
VARIANT lamId,loadId;
IIterator *lamIt,*loadIt;
IIterX *lamIterX,*loadIterX;
ULONG pCeltFetched;
...
db->get_iter_laminateId((IDispatch**)&lamIt);
lamIt->get_newEnum((IUnknown**)&lamIterX);
db->get_iter_loadId((IDispatch**)&loadIt);
loadIt->get_newEnum((IUnknown**)&loadIterX);
lamIterX->Reset();
for (lamIterX->Next(1,&lamId,&pCeltFetched);pCeltFetched>0;
lamIterX->Next(1,&lamId,&pCeltFetched)) {
printLamProperties(db,os,lamId);
loadIterX->Reset();
for (loadIterX->Next(1,&loadId,&pCeltFetched);pCeltFetched>0;
loadIterX->Next(1,&loadId,&pCeltFetched)) {
printLoadResponse(db,os,lamId,loadId,0.0,criteria);
}
}
lamIterX->Release();
lamIt->Release();
loadIterX->Release();
loadIt->Release();
Actually, the example shows that the component that is being developed is adapted to the use with languages that support the Microsoft IDispatch interface. However, a library adapted to the use with C++ language should also be developed. Consequently we do not advise to use the component from C++ or C language.
No C example is provided. But it is possible to program a C program using FeResPost COM component as well as a C++ program. This requires the same header files as those used in the C++ example. The program will not be significantly different than the C++ one. (Just a bit more complicated actually.)
The three examples described below are provided in directory “COMEX/EX02”. From now on, the access to the component is done by calling “getCurrentFrpApp” method defined in “Util” Module. (This reduces the amount of work necessary to update the examples when a new version of FeResPost is published.)
The file “COMEX/EX02/testNastranDb.py” contains python examples of the use of NastranDb class with the COM component. Each type of test is defined in a devoted python function that is called by the “main” program.
“testIterators” reads a Nastran BDF and a Patran session file into a NastranDb dataBase. Then the different iterators are tested and the “iterated” entities returned by the iterators are printed in an output file.
“testElemConnectivity” prints the elements connectivity for all the elements.
The example “COMEX/EX02/properties.rb” illustrates the access to FEM definition with “fillCard” method.
The file “COMEX/EX02/elemConnectivity.rb” contains the ruby equivalent of the “testElemConnectivity” function in “COMEX/EX04/testNastranDb.py” example. The operations done in this ruby file correspond to the ones in example “RUBY/EX16/elemConnectivity.rb” except that the COM component is used instead of the ruby extension. The comparison of the two ruby files shows that the differences correspond to the access to the component, and to the use of iterators.
The file “COMEX/EX02/testGroups.py” contains python examples of Groups manipulation with the COM component. Four functions performing different tests are defined:
“testGroupFunction1” reads a Nastran BDF and a Patran session file into a NastranDb dataBase. Then a loop on the Groups is done and the number of each type of entity present in each Group is printed.
“testGroupFunction2” reads a Nastran BDF and a Patran session file into a NastranDb dataBase. Then the different operators are tested.
“testGroupFunction3” reads a list of Groups from a Patran session file without inserting them into a DataBase. Then, a loop is done on the Array containing the Groups and the Group names and objects are printed.
“testGroupFunction4” reads a Nastran BDF and a Patran session file into a NastranDb dataBase. Then, Groups are build by association to materials.
The "main" function is defined at the bottom of the example file.
In the following sub-sections, one presents examples devoted to the manipulation of Result objects with FeResPost COM component. All these examples are the translation of examples of the “RUBY” directory for which the ruby extension was used. As descriptions of these examples with ruby extension are already given in Chapter IV.2, one highlights here only the peculiarities related to the use of the COM component.
Also, several of the ruby examples are translated in python. There, one also presents the peculiarities of the python programming with the COM component.
This example is stored in file “COMEX/EX03/printResLists.rb”. It corresponds to the example "RUBY/EX04/printResLists.rb" described in section IV.2.4. The differences between the two programs are related to the way FeResPost COM component is accessed, to the access to the objects of different classes, and to the use of iterators. (See corresponding explanations in section IV.2.4.1.)
The same example is also translated in python in file “COMEX/EX03/printResLists.py”. Here again, for explanations on the access to COM component and the use of iterators, the user is referred to section VII.1.4. One notes however differences in the use of iterators that return several values. The following ruby statements:
db.iter_resultKey.each do |lcName,scName,tpName|
tmpRes=db.getResultCopy(lcName,scName,tpName)
printf("%-20s%-15s%-50s%-10d\n",lcName,scName,tpName,\
tmpRes.Size)
end
become in python:
for tab in db.iter_resultKey:
lcName=tab[0]
scName=tab[1]
tpName=tab[2]
tmpRes=db.getResultCopy(lcName,scName,tpName)
stdout.write("%-20s%-15s%-50s%-10d\n"%(lcName,scName,tpName,\
tmpRes.Size)
(The differences are related to the fact that python has no syntax for iterators that return several values.)
This example is stored in file “COMEX/EX03/printStressMax.rb”. It corresponds to the example “RUBY/EX05/printStressMax.rb” described in section IV.2.4.2. This example illustrates the use of operators with COM component. For example, with ruby extension, the intersection of two Groups is calculated with the following statement:
newGrp = panelGroup * matGrp
With COM component, the same instruction becomes:
newGrp = panelGroup.opMul(matGrp)
So far, the difference is not very dramatic. However, the translation of expressions involving several dyadic operators can be more difficult. For example, the following expression with ruby extension:
scalar = Post.sqrt(sXZ*sXZ+sYZ*sYZ)
becomes with COM component:
scalar = frpApp.sqrt(sXZ.opMul(sXZ).opAdd(sYZ.opMul(sYZ)))
(Note also that the “sqrt” method is found in “frpApp” Application instead of “Post” module.) A python version of the example is also available in file “COMEX/EX03/printStressMax.py”.
This example is stored in file “COMEX/EX03/makeGravForces.rb”. It corresponds to the example “RUBY/EX06/makeGravForces.rb” described in section IV.2.5.1. As a Module is defined in this example, one needs to store the application in a ruby global variable. This is done as follows:
$frpApp = WIN32OLE.new("FeResPost_3_4_0.Application")
Then, in the different methods of the Module, the global variable can be used to access the different methods of the application. For example, objects of the different classes can be created with “newObject” method as follows:
db=$frpApp.newObject("NastranDb")
This example is stored in file “COMEX/EX03/printBeamForces.rb”. It corresponds to the example “RUBY/EX08/printBeamForces.rb” described in section IV.2.4.4. The example is also defined in the python file “COMEX/EX03/printBeamForces.py”.
No remark is to be done about these programs, except that the “UTIL” modules are used. These are defined in files “COMEX/Util/util.rb” and “COMEX/Util/util.py” for ruby and python respectively. When the ruby and python versions of the module are compared, one notes a difference in the use of iterators. The brackets are mandatory for iterators methods with arguments are used in python even when no argument is given. This means that the following ruby statement:
res.iter.each do |key,values|
Becomes in python:
for tab in res.iter(): key=tab[0] values=tab[1]
(The void brackets in python first statement is related to the fact that the “iter” method of “Result” class may have up to five arguments.)
Note that the UTIL Modules in COM examples correspond to the UTIL module defined in file “RUBY/UTIL/util.rb” and described in section IV.2.1.
This example is stored in file “COMEX/EX03/printStrain.rb”. It corresponds to the example “RUBY/EX08/printStrain.rb” described in section IV.2.4.4. The example is also defined in the python file “COMEX/EX03/printStrain.py”. No remark is to be done about this example.
These examples are stored in files “COMEX/EX03/modifCS2D.rb”, “COMEX/EX03/modifCS2Db.rb”, “COMEX/EX03/modifCS2Dc.rb” and “COMEX/EX03/modifCS3D.rb” respectively. They correspond to the examples of directory “RUBY/EX09” described in section IV.2.4.5. The example “COMEX/EX03/modifCS2Db.rb” is also programmed in python in file “COMEX/EX03/modifCS2Db.py”. No remark is to be done about these examples.
This example is stored in file “COMEX/EX03/testGlobFM.rb”. It corresponds to the example “RUBY/EX08/testGlobFM.rb” described in section IV.2.5.3. The example is also defined in the python file “COMEX/EX03/testGlobFM.py”. No remark is to be done about this example.
This example is stored in file “COMEX/EX03/writeGmsh.rb”. It corresponds to the example “RUBY/EX08/writeGmsh.rb” described in section IV.2.4.4. The example is also defined in the python file “COMEX/EX03/writeGmsh.py”. No remark is to be done about this example.
The examples described in the following sub-sections are devoted to the manipulation of XDB Result files. Only the second example deals with the manipulation of complex Results.
The first example is stored in file “COMEX/EX04/printXdbLcScResNames.rb”. It corresponds to the example “RUBY/EX17/printXdbLcScResNames.rb” described in section IV.2.4.6. The second example is stored in file “COMEX/EX04/printXdbLcInfos.rb”. It corresponds to the example “RUBY/EX17/printXdbLcInfos.rb” described in section IV.2.4.6. No remark to be done about these examples.
This example is stored in file “COMEX/EX04/manipComplex.rb”. It corresponds to the example “RUBY/EX17/manipComplex.rb” described in section IV.2.4.6. Some of the methods in ruby extension involve Complex arguments. As complex numbers are not accepted by the COM component, these numbers are replaced by an Array of two real values corresponding to the real and imaginary parts of the complex number respectively. This means that the following statements, valid when FeResPost ruby extension is used:
Z=Complex.new(3.0,2.0) multRI=resRI.clone multRI*=Z
become the following statements when the COM component is used:
Z=Complex.new(3.0,2.0) multRI=resRI.makeCopy() multRI=multRI.opMul([Z.real,Z.image])
One presents in the following sub-sections various examples of programs in which the COM component is used to perform CLA analyses.
This example is stored in file “COMEX/EX05/testShear.rb”. It corresponds to the example “RUBY/EX14/testShear.rb” described in section IV.3.5.
No remark to be done about this example.
This example is stored in file “COMEX/EX05/testClaFem.rb”. It corresponds to the example “RUBY/EX15/testClaFem.rb” described in section IV.3.6. Just one remark about this example: the COM methods do not accept the ruby “Hash” arguments. Therefore, this argument must be translated into Arrays the elements of which are Arrays of two elements corresponding to the keys and values respectively. In ruby, this operation is done by calling the “to_a” method of Hash class. For example, the insertion of allowables in a Laminate is done as follows:
lam=compDb.getLaminateCopy(6)
allowables={}
allowables["sc"]=200.0e6
allowables["s1c"]=200.0e6
...
allowables["s12"]=100.0e6
allowables["ilss"]=30.0e6
lam.insertAllowables(allowables.to_a)
compDb.insertLaminate(lam)
The example is also translated in python in file “COMEX/EX05/testClaFem.py”. Then, the “items” method of “map” class is used to produce an Array suitable for allowables insertion:
lam=compDb.getLaminateCopy(6)
allowables={}
allowables["sc"]=200.0e6
allowables["s1c"]=200.0e6
...
allowables["s12"]=100.0e6
allowables["ilss"]=30.0e6
lam.insertAllowables(allowables.items())
compDb.insertLaminate(lam)
Note also the use of “Dispatch” method in python to retrieve Result objects from an Array like in the following statements:
for tab in outputs: id=tab[0] res=Dispatch(tab[1]) util.printRes(os,id,res)
(We presume that the “Dispatch” statement is necessary to convert a VARIANT.)
This example is stored in file “COMEX/EX05/testCriteria.rb”. It corresponds to the example “RUBY/EX15/testCriteria.rb” described in section IV.3.6. No remark is to be done about this example.
The COM examples in directory “TESTSAT/COM/EX27” are a simple translation of the ruby example discussed in section IV.2.11. COM examples are written in ruby language and do not differ much from the examples using ruby extension.
In directory “COMEX/EX07”, one presents the source files of an object-oriented post-processing using the COM component. This is a transposition of the “PROJECTb” post-processing described in Chapter X.E.4. Modifications in the ruby sources are done to adapt the instructions to the fact that COM component is used instead of ruby extension. Also a few calls to the garbage collector have been added.
In directory “COMEX/EX08”, one presents the source files of examples illustrating the access to Results from XDB attached files. The four examples correspond exactly to the ones presented in section IV.2.4.7 for the use of ruby extension. Except for the few first lines, the examples are identical. One does not discuss the programming details here.
One advantage of programming FeResPost as a COM component, is that this allows to use the component from other applications. For example, FeResPost can be used from Excel provided one accepts to write some programming functions and subroutines in VBA. Several examples illustrate the benefits of using FeResPost from excel:
In Chapter VII.2 one shows how a small tool devoted to the automation of Classical Laminate Analysis can be developed in Excel.
The extraction of Results in Excel from a Nastran XDB file is illustrated in Chapter VII.3.
One shows in Chapter VII.4 how an entire post-processing project can be developed in excel. This project allows to define the data in excel while the actual calculations are managed by the programmed VBA modules that call FeResPost objects and methods.
A very small example illustrating the use of BLOB and SQL with VBA in section VII.1.9.
This example is presented in excel workbook “blob_test.xlsm” in directory “TESTSAT/COMEX/EX11” correspond approximately to the ruby examples of section IV.2.6. In this case, one uses the “SQLite for Excel" extension found on “http://sqliteforexcel.codeplex.com/”. The corresponding libraries and VBA Module are distributed with the example in sub-directories. Very small modifications have been brought to the VBA code “SQLite for Excel" to deal with the blobs produced by FeResPost. (See the “SQLite3” module in the sources that correspond to the corresponding Module found on “http://sqliteforexcel.codeplex.com/” + a few modifications.
Worksheet “MANIP” in the workbook corresponds to two VBA macros that perform operations very similar to those of the ruby example of section IV.2.6. These macros and a few more are defined in Module “FeResPost_Results” that contains the code for the example.
More information on the use of FeResPost with VBA is given in Chapters VII.2, VII.3 and VII.4. Note also that the installation of “SQLite for Excel" extension in subdirectories of the example directory is not necessarily a good idea. The extension should be installed in a proper directory if you want to use it for other applications. Then a tuning of some directory names in VBA source code will be necessary.
Note also that COM wrappers of SQLite are also available and may be used with VBA language. (See the following address “http://www.sqlite.org/cvstrac/wiki?p=SqliteWrappers” if you are interested.) Of course, the use of databases other than SQLite is also possible (MySQL, PostGreSQL...).
In the examples of section VII.1.4, one shows how the FeResPost COM component can be used to automate CLA calculations with different programming languages. However, the small programs done with these examples are not significantly different than the programs presented in Chapter IV.3.
One presents here an example in which the COM component is used in excel and allows to perform operations where the capabilities of excel and FeResPost are used together to produce a small application devoted to CLA calculations. The example is presented in excel spreadsheet “COMEX/EX06/LaminateAnalysis.xlsm”.
The presentation of the example is organized as follows:
One explains in section VII.2.1 how the excel workbook must be prepared to make the example work.
The different spreadsheets defined in the workbook are presented in section VII.2.3.
Some explanations on the different modules defined in the workbook are given in section VII.2.4
The example is meant to be the presentation of a small application devoted to classical laminate analysis. This application is highly customizable provided the user is ready to adapt it to its needs by modifying the spreadsheets and the associated VBA programming.
Before using the excel workbook, the FeResPost COM component must be referenced. This is done as follows:
The COM component must have been properly installed as explained in section X.A.4.5.
Then, open the excel workbook.
Open in the VBA editor: “Tools –> macros –> VisualBasic Editor”, or more simply key in "Alt+F11".
In VBA editor, you must reference the library. Go in “Tools –> References”, and select the appropriate version of FeResPost COM server. In the list, the name of the COM server should look like “FeResPost 5.0.9 COM server”.
Once this has been done, you may save the excel workbook so that the references to FeResPost library shall be “remembered” the next time you open the workbook.
If a FeResPost COM server is already referenced in the workbook when you open it the first time. (As it probably will be the case with the workbook you download from FeResPost web site.) You must first un-select the old reference to FeResPost server, before selecting the new one. You will have to perform this operation each time you install a new version of FeResPost COM server on your computer.
When you change the version of FeResPost, you must also modify the variable “appName” in the VBA code associated to “ClaDbIds” spreadsheet of the workbook. The corresponding line looks like:
Const appName As String = "FeResPost_4_5_4.Application"
Two events are defined in the workbook:
The “BeforeClose” proposes to save the current ClaDb database into an NDF file, and into the “NeutralLines” spreadsheet before quitting the workbook. Note that if you save the database into the “NeutralLlines” spreadsheet, you also must save the excel workbook if you want to retrieve you data the next time you open it.
The “Open” event starts the FeResPost application and retrieves the ClaDb dataBase stored in the “NeutralLines” spreadsheet when the workbook is opened. This is the place to modify if you want to modify the behaviour of FeResPost, in particular for the out-of-plane shear calculation. The method looks as follows:
Sub workbook_Open()
Dim locDb As Variant
Dim tmpLam As Variant
Dim x As Variant
’
ChDrive (VBA.Left(ActiveWorkbook.Path, 1))
ChDir (ActiveWorkbook.Path)
’
x = Environ("NUMBER_OF_PROCESSORS")
x = Environ("PATH")
’ClaLam.setOopsApproach ("Standard")
’ClaLam.setMuxMuy 0.7, 0.8 ’ Arbitrary values here...
ClaLam.setOopsApproach ("UncoupledXY")
’ClaLam.setOopsApproach ("InShearLoadingAxes")
Set locDb = Feuil1.getDb
Call Feuil14.initDbFromStoredNeutralLines
Call Feuil1.updateMaterialIds
Call Feuil1.updateLaminateIds
Call Feuil1.updateLoadIds
End Sub
(The call to “setOopsApproach” allows to change the out-of-plane shear calculation approach.)
One presents below the different spreadsheets defined in the workbook. Most of these spreadsheets also contain associated VBA functions and variables. Generally, these are used for the spreadsheet buttons automation.
This spreadsheet is hidden. But you can make it “Visible” with the VBA editor. The spreadsheet contains the definition of several list that are used by the automation buttons of the other spreadsheets in the workbook. No VBA functions or variables are associated to “HiddenData” spreadsheet.
This spreadsheet is hidden. But you can make it “Visible” with the VBA editor. The spreadsheet contains the neutral lines corresponding to a ClaDb object in NDF format. (See the presentation of “ClaDbIds” spreadsheet for more information.) No VBA functions or variables are associated to “NeutralLines” spreadsheet.
This is the spreadsheet that manages the access to the COM server and the ClaDb composite database used for calculations. This is the first spreadsheet in which you have to go to start the application.
The spreadsheet contains several buttons, and information on the entities available in the current dataBase appear in the cells: lists of materials, laminates and loads. Each entity in the current dataBase is characterized by:
An integer ID,
A String ID,
an excel ID.
The integer and string id correspond to the CLA idfier of the entity. The excel ID is a String representation of this idfier that allows to refer to the entities in the other spreadsheets. The spreadsheet defines several buttons:
The ComboBox button allows to select the type of file from which a DataBase shall be read or DataBase entities shall be imported. This file format must be correctly defined for the file read/import operations to work properly. Four file formats are possible: “ESAComp" EDF file, FeResPost neutral data file (NDF), Nastran BDF bulk data file, and Samcef DAT banque file.
The “Read Data File” button is used to read a new ClaDb database. All the entities stored in the current dataBase are first deleted. Note that the ComboBox button must have been properly set before reading entities.
The “Import Data File” button performs the same operation, but the entities that have been read are added to the current dataBase. (They also replace the old entities that have the same ID.)
Three command buttons perform the same operation as “Import Data File” button except that each time, only one type of entities is read: “Import Laminates”, “Import Materials” and “Import Loads” buttons.
The button “Save FeResPost NDF file” is used to save the composite DataBase in a neutral data file. (Only neutral Data files can be saved by FeResPost.)
The button “Show/Hide FeResPost” is used to show or hide the FeResPost server window. Note that the FeResPost server continues to run, even when it is hidden.
The button “Close FeResPost” really closes the FeResPost server. When this is done, the composite dataBase is closed too, but its content is not saved! (so be careful with this button.)
The button “Delete Selected Entities” is used to remove entities from the composite dataBase. To use this button you must first select a range in the entities that appear below, then press the button. To select a range, at least the three columns corresponding to the entities you want to remove must be selected.
The two buttons “SaveDbToNeutralLines” and "RetrieveDbFromNeutralLines” are used to store the current DataBase into the hidden “NeutralLines” spreadsheet. This allows you to recover the db you wore working with the last time you used the workbook without reading an NDF file. (Of course you have to save the excel workbook before quitting.)
Several macros are defined in the spreadsheet. Most of these macros perform the different operations done by the buttons. You can access to the macros by the VBA editor. At the beginning of VBA program lines, several variables are defined:
Dim frpApp As Variant Dim db As Variant Dim maxEntitiesNbr As Long Const maxPliesNbr As Long = 100 Const appName As String = "FeResPost_3_4_0.Application" Const logFileName As String = "FeResPost_LaminateAnalysis.log"
frpApp is the variable that contains a reference to the FeResPost COM server. db contains the ClaDb composite dataBase in which all composite entities are stored. Only one ClaDb dataBase can be opened in the workbook. The variable “appName” is a constant that corresponds to the name of the server. You will have to change this variable when you change the version of FeResPost.
The logFileName variable is used to redirect FeResPost output messages. This is necessary, as with excel, FeResPost is not run in console mode. Practically, the redirection is programmed as follows in “getApplication” method:
fullLogName = ActiveWorkbook.Path + "\" + logFileName frpApp.openMsgOutputFile fullLogName, "w+" frpApp.writeAboutInformation
The spreadsheet allows to manipulate the units in which The CLA database and its entities are expressed:
Seven ComboBox buttons allow to select the units for length, mass, force...
The “SetDbUnits” button sets the units system associated to the composite database but does not change anything to entities stored in the DB.
The “SetUnitsAllEntities” button sets the system of units of the CLA database and of all its entities (materials, laminates and loads).
The “SetUnitsAllMaterials” button sets the units of all material entities stored in the database.
The “SetUnitsAllLaminates” button sets the units of all laminate entities stored in the database.
The “SetUnitsAllLoads” button sets the units of all load entities stored in the database.
The “ChangeUnitsAllEntities” button changes the system of units of the CLA database and of all its entities (materials, laminates and loads).
The “ChangeUnitsAllMaterials” button changes the units of all material entities stored in the database.
The “ChangeUnitsAllLaminates” button changes the units of all laminate entities stored in the database.
The “ChangeUnitsAllLoads” button changes the units of all load entities stored in the database.
Remember that the difference between the “SetUnits*” and “ChangeUnits*” methods is that the second group of methods perform units conversions between old and new units. The “SetUnits*” methods modifies the units associated to entities without modifying the values of the different quantities.
Presently, the workbook does not allow to modify the system of units of CLA entities individually. This could be done by the addition of a few buttons in the corresponding “MatEdit”, “LamEdit” and “LoadEdit” worksheets. We think however that it is a bad idea to try to define CLA entities with different units in a same database. Actually, the number of buttons defined in “DbUnitsEdit” spreadsheet is probably already too large.
This spreadsheet is used to edit materials defined in the current dataBase. New materials can also be added. The spreadsheet contains two buttons:
The ComboBox button allows to retrieve the definition of a material defined in the current DataBase in ClaDbIds spreadsheet. The excel ID is used to retrieve the material.
The “Insert in DataBase” button is used to insert the defined material in the DataBase.
The material IDs and properties are defined by filling the different cells where appropriate.
This spreadsheet is used to edit laminates defined in the current dataBase. New laminates can also be added. The spreadsheet contains three buttons:
The ComboBox button allows to retrieve the definition of a laminate defined in the current DataBase in ClaDbIds spreadsheet. The excel ID is used to retrieve the laminate.
The “Insert in DataBase” button is used to insert the defined laminate in the DataBase.
The “Existing Material Search” ComboBox button is only used to retrieve the exact integer and String IDs of a material that exists in the DataBase and make the definition of additional plies easier.
The laminate IDs and properties are defined by filling the different cells where appropriate.
This spreadsheet is used to edit loads defined in the current dataBase. New loads can also be added. The spreadsheet contains two buttons:
The ComboBox button allows to retrieve the definition of a load defined in the current DataBase in ClaDbIds spreadsheet. The excel ID is used to retrieve the load.
The “Insert in DataBase” button is used to insert the defined load in the DataBase.
The load IDs and properties are defined by filling the different cells where appropriate.
This spreadsheet calculates material properties for a material defined in the current composite dataBase. The two buttons allow to select an existing material and the orientation wrt which material properties are calculated.
The spreadsheet makes use of several functions defined in “calcMatProperties” VBA module.
This spreadsheet calculates laminate properties for a laminate defined in the current composite dataBase. The two buttons allow to select an existing laminate and the orientation wrt which laminate properties are calculated.
The spreadsheet makes use of several functions defined in “calcLamProperties” VBA module.
This spreadsheet allows to visualize the definition of laminates in a format suitable to inclusion in text documents. The spreadsheet makes use of “getLamDescr” function defined in “calcLamProperties” VBA module. This function has two arguments: the name of the laminate, and a list of acronyms that allow to replace material names in laminate description by a shorter name (typically a single letter).
This spreadsheet calculates laminate load response for a laminate defined in the current composite dataBase, and a loading also defined in the current dataBase. The buttons allow to select:
An existing laminate (in the active dataBase),
An existing load (in the active dataBase),
The orientation wrt which laminate properties are calculated,
Whether plies result outputs are requested at bottom, mid or upper surface of each layer,
Whether the ply stresses and strains are restituted in coordinate system related to laminate axes or in ply axes,
The last button gives the rotation angle wrt laminate axes of the restitution coordinate system. (This button is used only if the previous button is set to “YES”.
The spreadsheet makes use of several functions defined in “calcLamLoadResponse” VBA module. These methods calculate laminate global stress/strain state, ply stresses and strains, and failure indices, reserve factors or equivalent stresses.
This spreadsheet performs the same calculations as “LamLoadResponse_A” except that the loading is not extracted from the current composite dataBase. Instead the loading is defined in the spreadsheet by filling the appropriate cells. (No ClaLoad object defined in the composite database is used.) For all the quantities that appear in the spreadsheet, units are those of the laminate object.
This spreadsheet is used to calculate laminate minimum or maximum reserve factors, failure indices or equivalent stresses for a selection of load cases and criteria. This is the “matricial” version of the calculation where a whole set of load responses are calculated by a single call to one function. This version is generally very efficient when a large number of load cases must be processed. The unit system for components of loading and results is the same as for the laminate.
This is the scalar version of the spreadsheet above. It is generally less efficient. On the other hand, when cells defining applied loads are modified, the amount of re-calculations is reduced. This allows to decrease the calculation time between each cell modification.
Three VBA modules are defined. The modules define functions that can be used to obtain material properties, laminate properties, or laminate load response. These modules define functions that return results that are generally presented as 1D or 2D arrays, and can be used directly in excel spreadsheets with the appropriate arguments passed as selections of cells. The user should look at the VBA code to understand the different functions.
TIP: to enter a formula that returns a matricial function into an excel spreadsheet, select the target cell, enter the name of the function with the appropriate arguments and press “MAJ+ENTER” simultaneously.
These functions return different types of material properties like CMEs, CTEs, stiffness and compliance matrices... Examples of use of these functions are given in spreadsheet “MatProperties”.
These functions return different types of laminate properties like CMEs, CTEs, stiffness and compliance matrices... Examples of use of these functions are given in spreadsheets “LamProperties” and “LamText”.
The functions calculate laminate load responses. Examples of use of the functions are given in spreadsheets “LamLoadResponse_A”, “LamLoadResponse_B”, “LamMinMaxCalcArray”, “LamMiMaxfCalcScal”.
Note that for several of the functions, the load can be specified different ways depending on the size of the range that defines the loading:
If the range corresponds to one single cell, this cell is assumed to contain the excel ID of a ClaLoad object stored in the current DataBase.
If the selection corresponds to a range of 2 line and 9 columns, the elements are interpreted as a load defined explicitly.
In directory “COMEX/EX09”, one gives an excel workbook “PostXdbRandom.xlsm” devoted to the post-processing of finite element Results. More precisely, the excel workbook allows to access randomly Nastran XDB results attached to a NastranDb DataBase.
This spreadsheet is not very different than the one presented in Chapter VII.4. Indeed the global organization of the workbook is more or less the same with spreadsheets and modules devoted to specific tasks:
A Hidden spreadsheet called “FemHiddenData” contains some persistent data for menus or selections.
Spreadsheet “FemDbIds” is devoted to the access to finite element model and Results. This spreadsheet is discussed in section VII.3.2.
Spreadsheet “GroupEdit” that allows to manipulate groups stored in the current database. This spreadsheet is discussed in section VII.3.3.
Spreadsheet “ResExtract” performs simple extractions of Results on specified Groups. A description is given in section VII.3.4.
Spreadsheet “ResCombiliExtract” performs extractions of linear combination of Results on specified Groups. A description is given in section VII.3.5.
In “WorstResExtract” spreadsheet, presented in section VII.3.6, one shows that the spreadsheets may be used to select a certain number of values based on a specified criterion.
Spreadsheet “DynamResExtract” is devoted to the extraction of complex Results corresponding to dynamic response analysis. The spreadsheet is discussed in section VII.3.7.
Possible improvements of the excel spreadsheet are discussed in section VII.3.8.
The excel workbook makes use of the FeResPost COM component. This means that the component must be registered and referenced in the workbook. More information on this subject is given in section VII.3.1.
A Samcef version of the workbook is also given in directory “COMEX/EX09” (file “PostDesFacRandom.xlsm”). Its functionalities and principles are very similar to those of Nastran version.
Before using the excel workbook, the FeResPost COM component must be referenced. This is done as follows:
The COM component must have been properly installed as explained in section X.A.4.5.
Then, open the excel workbook.
Open in the VBA editor: “Tools –> macros –> VisualBasic Editor”, or more simply key in "Alt+F11".
In VBA editor, you must reference the library. Go in “Tools –> References”, and select the appropriate version of FeResPost COM server. In the list, the name of the COM server should look like “FeResPost 5.0.9 COM server”.
Once this has been done, you may save the excel workbook so that the references to FeResPost library shall be “remembered” the next time you open the workbook.
If a FeResPost COM server is already referenced in the workbook when you open it the first time. (As it probably will be the case with the workbook you download from FeResPost web site.) You must first un-select the old reference to FeResPost server, before selecting the new one. You will have to perform this operation each time you install a new version of FeResPost COM server on your computer.
When you change the version of FeResPost, you will also have to modify the variable “appName” in the VBA code associated to “FemDbIds” spreadsheet of the workbook. (More information on this subject is given in section VII.3.1.)
The spreadsheet is devoted to the management of finite element model and finite element Results. Several buttons can be used:
The two buttons “Show/Hide FeResPost” and “Close FeResPost” work exactly as in “LaminateAnalysis.xlsm” workbook. (See section VII.2.3.)
Button “Select Bdf File” is used to select the BDF file from which the finite element model shall be read.
Button “Select Ses File” is used to select the Patran Session file from which the definition of Groups shall be read.
Button “ReadModel” performs several operations:
If necessary the COM component is loaded and the FeResPost application is loaded.
A “NastranDb” object is created.
The BDF file previously selected is imported as model into the DataBase.
The Groups are initialized by reading the Patran Session File previously selected.
After the importation of model and Groups, the list of Groups and coordinate systems present in the DataBase are saved in the two first columns in the spreadsheet.
Button “Select Xdb File” is used to select the Nastran XDB Result file that shall be read.
Button “ScanXdb” scans the content of the previously selected XDB Result file and updates the lists of load cases, sub-cases and Result types in columns C, D and E.
Button “exportGroups” can be used to export Groups from the current DataBase in a Patran session file. This is useful only if the Groups have been manipulated in the “GroupEdit” worksheet. (Section VII.3.3.)
Note that the reading of a model and Results must be performed before using the other spreadsheets.
This spreadsheet allows to manipulate the Groups stored in current DataBase. In columns “A” to “G”, one presents several automation buttons that allow to manipulate directly the entities stored in a Group:
The name of the Group being manipulated is stored in cell “C3”. This name can be set manually, or selected in the menu just below if it already exists in the DataBase.
The entities to be set, removed or added are defined in columns “A” to “E” and lines 11 to ... Column “A” corresponds to entity types. Column “B” is used when a single entity is to be added to the Group. Columns “C” to “E” defines ranges by looping on the entity IDs. Some of the cells may be left void.
Button “Add Group to current Db” builds the Group defined by its name and entities and stores it in the DataBase. If a Group with the same name is already defined in the DataBase, it is replaced by the new Group.
Button “Add Entities to Existing Group” adds the defined entities to the entities of a Group already existing in the DataBase.
Button “Remove Entities from Existing Group” performs the reverse operation.
Four buttons allow to build new Groups by topological operations on existing Groups. The operations correspond to the four topological operators defined in “Group” class. The “Group1” and “Group2” operands must be existing Groups of the current DataBase. The resulting “Group3” can be already existing in the current DataBase or a new Group set manually.
This spreadsheet is used to perform simple extraction of Results but nothing more. (Except that modification of coordinate systems are also done.) Several ComboBoxes allow to define the parameters for the extraction:
Selection of the name of the Group on which the Results shall be extracted.
Selection of the load case name.
Selection of the sub-case name.
Selection of the Result type name.
Selection of the “location” parameter. For example “Nodes”, “Elements” “ElemCenters”... This parameter, together with the name of the Group determines on which element and node entities the Results are extracted.
The coordinate system in which the Result components shall be extracted. This is the only parameter corresponding to a post-processing calculation done on the Result.
A checkBox allows to specify whether the data are recovered in a projected coordinate system (when applicable). Then, three real values specify the components of the coordinate systems given in the selected coordinate system.
It is possible to select the layers on which results will be extracted (when applicable). The choice is between “all layers” (no layers selection) or a range address. The range corresponds to a selection of cells in which the layers are given.
When all the parameters have been defined, the “Extract” button performs the extraction and fills cells in the spreadsheet starting at line 15. More precisely, the following operations are done in the corresponding VBA subroutine:
The current NastranDb DataBase is retrieved using method “getDb” of FemDbIds spreadsheet.
The names of selected load case, sub case and result type are used to import Results into the current DataBase. (The XDB file name has been selected in “FemDbIds” spreadsheet.)
The Group corresponding to the selected Group Name is retrieved from the current DataBase. (“getGroupCopy” method of NastranDb class.)
This Group, the selected location and the names of load case, sub-case and result type are used to retrieve a Result from the DataBase using “getResultCopy” method.
The Results stored in the DataBase are removed by calling method “removeAllResults”.
If necessary, the components of the Result are expressed in a new coordinate system by calling “modifyRefCoordSys” of “Result” class.
The previous results are erased.
The data are extracted from the Result and pasted into the spreadsheet starting at line 16.
A title line is added at line 15.
At different steps, an Error message is defined. This error message is printed at line 15 of the spreadsheet is an Error occurs during execution. In most cases, this error is related to inconsistencies in the definition of data. Then the error message should help the user to correct his data.
Note that this spreadsheet should work for real as well as complex Results.
The “ResExtractedCombili” worksheet allows the extraction of linear combinations of Results instead of elementary Results. In the VBA programming of the extraction this is simply done by calling method “getXdbAttachmentResultsCombili”. In this example, the linear combinations of Results extracted from the XDB files are limited to:
Combinations of 3 elementary load cases Results.
Moreover, the elementary Results must be read from a single XDB file.
The spreadsheet “WorstResExtract” is very similar to “ResExtract”. It is used to illustrate the possibility of writing small post-processing spreadsheets.
In this case, no coordinate system can be specified. Instead, one can select a criterion among a small predefined selection, and an integer number between 1 and 100 corresponding to the number of values that shall be extracted.
When the “Extract” button is clicked, the following operations are performed:
First, the same steps 1 to 5 as in section VII.3.4 are performed. The extracted Result is stored in “res” variable.
The selected criterion is calculated by calling among the methods “deriveScalToScal”, “deriveVectorToScal” and “deriveTensorToScal” the of “Result” class the one that is appropriate. A “tmpRes” Result is created.
One extracts the nbrVals largest values of this “tmpRes” Result by calling “extractResultForNbrVals” method.
Correspondingly, one also extracts the critical values of “res” Result using “extractResultOnResultKeys” method.
Finally, the data are printed in spreadsheet cells with appropriate title lines.
Instead of simply extracting FeResPost pre-defined scalar derived criteria, it should not be very difficult calculated more specific criteria by modifying the spreadsheet and associated VBA code. For example, you can try to modify the spreadsheet and calculate minimum reserve factors instead of maximum Von Mises stress.
The spreadsheet works with real Results only.
In this example, one shows how it is possible to use the COM component to investigate the Results of Nastran dynamic response analyses.
The main difference between this example and the simple result extraction of section VII.3.4, is that one no-longer selects a sub-case for Result extraction. Instead, the extraction is done for all the sub-cases corresponding to the specified load case. When Results are printed in the cells, each line corresponds to one sub-case (i.e. to one frequency).
The different entities are sorted in the columns of the spreadsheet. This limits somewhat the number of FE entities for which the Results can be retrieved. This is why the Group in this case is specified directly by defining the integer IDs of their elements and nodes. The Group is also defined by the specification of the type of entities that are inserted (“EntityTypeSelector” ComboBox).
One also decided to extract only one component for each value.
When all the parameters have been defined, the “Extract” button performs the following operations in the corresponding VBA subroutine:
The current NastranDb DataBase is retrieved using method “getDb” of FemDbIds spreadsheet.
The names of the different sub-cases found in the XDB file are retrieved by method “getXdbScNames” of “NastranDb” class and stored in an Array of Strings. This list of sub-case is used for the reading of Results from XDB file.
The names of selected load case, sub case and result type are used to import Results into the current DataBase. (One imports the Results for one load case, one Result type and all the sub-cases.)
The Group corresponding to the type of entities and the list of integers defined at left part of the spreadsheet is created. This Group shall be used to extract Results from the DataBase.
One uses method “getXdbLcInfos” of “NastranDb” class to obtain information on the load cases and sub-cases defined in the XDB file. The advantage of this method is that it provides the Results by increasing order of frequency and allows to retrieve easily the sub-case names, and their associated frequencies.
Then a loop is done on the difference sub-cases. For each sub-case:
One extracts the Result on the selected Group.
One modifies the reference coordinate system if necessary.
One extract the selected component.
One retrieves the magnitude and phase for the different entities.
An Array with the data is build. The lines of the Array correspond to the sub-cases. The columns correspond to the different entities and to the magnitude and phase. This Array is stored in variable “ret”.
The previous spreadsheet results are erased.
The content of “ret” Array is pasted into the spreadsheet starting at line 51.
The Results stored in the DataBase are removed by calling method “removeAllResults”.
The two graphics are updated to plot the magnitude and phase for the different entities.
The spreadsheet works with complex Results only.
It is possible to modify the different spreadsheets described above in order to perform more complicated operations. For example:
Allow the management of several DataBases, Patran session files or XDB attachments.
Allow the definition of linear combinations of Results with more that 3 elementary Results or with Results extracted from different XDB attachments.
...
(See also the Samcef version of the workbook is also given in directory “COMEX/EX09” and file “PostDesFacRandom.xlsm”.)
In directory “COMEX/EX10”, one gives an excel workbook “PostProject.xlsm” devoted to the automation of stressing of the satellite.
This example shows how FeResPost COM component can be used to build an excel project defining post-processing methods and data. More precisely, the purpose of this example is to define with excel a post-processing similar to the example of Chapter X.E.4 FeResPost ruby extension.
The advantage of using Excel and COM component, is that it is now possible to use Excel to define the different data of the detailed calculation, and several formatting functions. Actually the definition of data is no longer dispersed in the ruby programming code. At the same time, The use of functions in excel allows to define many things as the sequencing of calculations, the formatting of results, the calculation and archive of results for load cases or not...
Here again, the example is defined in a workbook that contains both worksheets (section VII.4.2) and VBA modules (section VII.4.3).
FeResPost is not programmed as a multi-threaded library, but some versions of excel are (2007 and later versions). Therefore, the multi-threaded calculation should be disabled in excel when FeResPost is used. (See the “advanced options” in excel.)
The use of FeResPost with excel “multi-threaded” option enabled may result in a multiplication of elapsed computing time by a factor 2 approximately.
Before using the excel workbook, the FeResPost COM component must be referenced. This is done as follows:
The COM component must have been properly installed as explained in section X.A.4.5.
Then, open the excel workbook.
Open in the VBA editor: “Tools –> macros –> VisualBasic Editor”, or more simply key in "Alt+F11".
In VBA editor, you must reference the library. Go in “Tools –> References”, and select the appropriate version of FeResPost COM server. In the list, the name of the COM server should look like “FeResPost 5.0.9 COM server”.
Once this has been done, you may save the excel workbook so that the references to FeResPost library shall be “remembered” the next time you open the workbook.
If a FeResPost COM server is already referenced in the workbook when you open it the first time. (As it probably will be the case with the workbook you download from FeResPost web site.) You must first un-select the old reference to FeResPost server, before selecting the new one. You will have to perform this operation each time you install a new version of FeResPost COM server on your computer.
When you change the version of FeResPost, you will also have to modify the variable “appName” in “DbAndLoadCases” VBA module of the workbook.
The application outputs an SQLite database that stores Results for different loadcases. (See “ResultsGMSH” module in section VII.4.3.5.) This means that the corresponding libraries must be installed on your computer. Note that these libraries are provided with the “TESTSAT/COMEX/EX11” example.
The variable “sqliteLibDirName” contains the path to the directory containing the “SQLite3” shared libraries. This variable must be adapted to match your installation.
Several types of worksheets are defined in the workbook:
Worksheets that contain the definition of databases and load cases. (More precisely, they contain the information needed to build databases and Results.) The characteristics of these worksheets are given in section VII.4.2.2.
Worksheets that allow to select load cases, and associate parameters to each load case. Section VII.4.2.3 presents these worksheets.
The “LcSelector” worksheet that automates several operations. Only one such worksheet can be defined in the workbook. It is presented in section VII.4.2.1.
The post-processing worksheets that define the data and sequence of operations to perform post-processing calculations, and archive Results. More information about these worksheets is given in section VII.4.2.4
One worksheet called “envelopeGMSH” and devoted to the manual production of GMSH envelope of Results.
Several worksheets have been added to test the post-processing of Samcef results:
Worksheet “SamcefDefDbLc” defines a database and several load cases.
Worksheet “SamcefSel” defines the corresponding selection with associated parameters.
Worksheet “post_samcef” tests the post-processing of samcef results by extracting results and calculating a few margins of safety.
Note that the finite element model and results corresponding to these samcef post-processing are not provided, so that you cannot work the samcef example.
This worksheet is used to select the definition of databases and load cases, and to select a sub-set of load cases that shall be post-processed. Two data must be entered “manually” (they appear in blue in the worksheet):
The name of the worksheet in which the definition of databases and load cases is provided.
The name of a worksheet containing a selection of load cases and defining the associated parameters.
The worksheet also defines several automation buttons:
“ReadDbAndLoadCases” is used to read the definition of databases and load cases, and the selection of load cases and parameters. The names of the two corresponding worksheets must first be defined in the appropriate cells below the “ReadDbAndLoadCases” button. This button is the first to use after opening the workbook. Indeed, this button initializes lists of load cases and databases in the “LcSelector” worksheet and several variables in “DbAndLoadCases” module.
The ComboBox allows to manually select and calculate a load case.
The “ArchiveResults” button can be used to manually archive the calculated Results in a separate workbook.
The “ReinitArchiveResults” button reinitializes all the VBA variables related to the archiving of calculated Results.
The “WriteGmshFiles” button performs the writing of Results in GMSH files.
The “ReinitGmshFilesList” clears all the variables related to the archiving of Results into GMSH files.
The “LoopOnLoadCases” button performs the calculations for all the selected load cases and archives the Results in a separate workbook.
“Reinit FeResPost Objects” button re-inits all the variables defined in the VBA project, which restarts from scratch.
“Debug Current Load Case” button prints in the standard output file debugging information about the current load case.
More information on the archiving of Results and the creation of GMSH files is provided in the sections devoted to the corresponding VBA modules.
One or several worksheets defining databases and load cases can be defined in the workbook. However, only one such worksheet can be selected in “LcSelector” worksheet. The content of the worksheet must comply with certain conventions:
The ten first lines are never taken into account.
Otherwise each line defines a peculiar entity:
An elementary load case if the first column contains “LC_ELEM” keyword.
A load case combining linearly elementary load cases if the first column contains “LC_COMBILI” keyword.
A NastranDb database if the first column contains “NASTRANDB” keyword.
A SamcefDb database if the first column contains “SAMCEFDB” keyword.
All the lines of which the first element does not contain one of these keywords are ignored.
For valid lines (un-ignored ones), the second column corresponds to an identifier of the entity that is defined.
The other columns contain information defining the object:
For NastranDb databases, several keywords allow to define the operations that are performed when a database is created:
The first keyword in the first column is “NASTRANDB" and is followed immediately by an identifier allowing to retrieve the entities and information associated to the database.
The keyword “GMSH” specifies that the value in the following column contains the name of a GMSH file in which the Nastran model is saved in GMSH format.
The “BDF” keyword specifies that the following column contains the name of a file from which the Nastran finite element model is read.
The “SESSION” keyword specifies that the columns that follow contain names of Patran Group session files containing the definition of Groups.
The “CLADB” keyword specifies that the columns that follow contain the sources in which information is read to build the ClaDB object in which compoiste entities are defined. Sources correspond to the names of NDF files in which composite databases are stored. If a cell contains the name of the NastranDb currently being defined, the composite entities defined in the corresponding finite element model are imported into the database. If the keyword is omitted, then the ClaDb is produced by extraction of the NastranDb database that is build.
For SamcefDb databases, several keywords allow to define the operations that are performed when a database is created:
The first keyword in the first column is “SAMCEFDB" and is followed immediately by an identifier allowing to retrieve the entities and information associated to the database.
The keyword “GMSH” specifies that the value in the following column contains the name of a GMSH file in which the Nastran model is saved in GMSH format.
The “DAT” keyword specifies that the following column contains the name of a Samcef Bacon “banque” file from which the Samcef finite element model is read.
The “SESSION” keyword specifies that the columns that follow contain names of Patran Group session files containing the definition of Groups.
The “GROUPDAT” keyword specifies that the columns that follow contain names of a Samcef Bacon “banque” files from which the definition of Groups shall be read.
The “CLADB” keyword specifies that the column that follows contains the name of the NDF file from which a ClaDb composite database is read. If the keyword is omitted, then the ClaDb is produced by extraction of the SamcefDb database that is build.
The “SESSION” and “GROUPDAT” keywords are the only ones that may be followed by several columns.
For elementary load cases, one provides:
In the first column, the keyword “LC_ELEM” followed in the second column by the name of the load case. This is the name by which the load case shall be referred to in the rest of the worksheet.
In the third column, one gives the name of the database associated to the load case. This corresponds to the database that shall be used for all the post-processing operations of this load case Results. The choice of the associated database can be superseded by defining parameter “FEMDB” at load cases selection level. (See section VII.4.2.3.)
The fourth column contains a keyword corresponding to the type of Result file that shall be accessed. Presently, Only two values are allowed:
Columns 4 may contain the keyword “XDB”. Then, an XDB attachment to a NastranDb database is defined and...
In column 5, one provides the access path to the XDB file.
In column 6, one provides the name of the load case in the XDB file. This name does not necessarily correspond to the “FeResPost” name specified on the second column.
Finally, the identification of the subcase is provided in column 7.
Columns 4 may contain the keyword “DESFAC”. Then, a DESFAC attachment to a SamcefDb database is defined and...
In column 5, one provides the access path to the DES file.
In column 6, one provides the access path to the FAC file.
In column 7, one provides the name of the load case in the DES/FAC file. (Default name generated by FeResPost when the file is attached.) This name does not necessarily correspond to the “FeResPost” name specified on the second column.
Finally, the identification of the subcase is provided in column 8.
Note that XDB files must be attached to NastranDb databases, and DESFAC files to SamcefDb databases.
For combined load cases, one provides:
In the first column, the keyword “LC_COMBILI’ followed in the second column by the name of the load case. This is the name by which the load case shall be referred to in the rest of the project.
In the third column, the number of elementary load cases used in the linear combination.
The following columns define pairs of real and string values corresponding to the factors and names of elementary load cases used for the linear combination of Results. These load cases must have been defined on “LC_ELEM” lines.
One or several worksheets define selections of load cases and associated parameters. The first line is a title line. It also defines the names of parameters that are defined for each selected load case. The following lines define the load cases and parameters:
In the first column, one defines the name of the load case.
The other columns define parameter values.
One notes that one load case can be defined in different “selection” worksheets with identical or different parameter values. The “TempLoad” parameter is used here to associate a load case name to an integer ID corresponding to the name of the temperature field used by Nastran to load the structure. This value is used by some post-processing functions to retrieve the temperature fields stored in an SQLite database. (See the “recoverTemp.rb” example in section IV.2.8.5.)
The “FEMDB” parameter name is a reserved one. It allows to force the association of one or several load cases to a particular finite element database. This can be handy when one tries to avoid the definition of too many different databases. The associated value is a String corresponding to the identifier attributed to the database in the databases and load cases definition worksheet.
Those are the worksheets in which the detailed data of post-processing are defined. Four such worksheets are defined so far: “post_connect” is devoted to the post-processing of connection loads, “post_sandwich” is devoted to the post-processing of stresses in sandwich panels, and “post_composite” uses the function “getCompositeRf” that calculates reserve factors using the classical laminate analysis. Worksheet “post_extract” has been added to illustrate the extraction of Results on lists of elements and/or nodes defined explicitly in ranges of cells.
These worksheets mainly use the functions defined in “ExtractionCriteria”, "ResultsExtraction", and “ResultsArchiver” modules. Basically, they define the data, and perform the call to functions of these modules. One makes several remarks about the use of these worksheets:
The number of worksheets could be increased if necessary without problem. So far, one created three post-processing worksheets, each being devoted to a peculiar type of post-processing (connections, stresses or extraction). However, other types of separations are possible: type of margin, part of the structure...
One also uses the “getParameter” function of “DbAndLoadCases” VBA module to obtain the appropriate safety factors.
The functions must depend directly or indirectly on the current load case name if one wants them to be re-calculated each time the selected load case is modified. This means that all the functions refer directly or indirectly to the corresponding cell in “LcSelector” worksheet.
One separates the calls to the post-processing function from the formatting of Results for archiving. This formatting is used to:
Select the values that shall be archived,
Modify units (MPa instead of Pa, mm instead of m...),
Perform additional calculations (calculation of margins of safety),
...
Calls to “saveToArchive” function are done to allow to archive calculated Results. (This is particularly useful when one performs loops on a selection of load cases.)
This worksheet is used to generate “manually” the GMSH files containing the envelopes of Results. More precisely, a selection of load cases is read, and the corresponding Results retrieved from “” SQLITE database are retrieved and used to generate envelopes of Results that shall be saved in GMSH files.
This is done by clicking the “Save GMSH envelope” button. The arguments of the corresponding subroutine are stored in two cells:
Cell C6 contains the name of the spreadsheet in which the selection of load cases shall be read. This spreadsheet can be the sheet “envelopeGMSH” itself, or another worksheet defining the selection. The first column of the worksheet is read and a list of load cases is generated.
Cell C7 contains the access path to the main BDF files used to generate the database that shall be used for the generation of GMSH files.
One presents below the different modules that have been defined in the project.
This module is closely related to the definition of databases and load cases. It manages the recovery of information needed to create the databases, and to generate and read the Results corresponding to the different load cases. Several variables corresponding to the lists of databases, elementary and combined load cases are defined in the module. For example:
“appName” allows to retrieve the appropriate version of FeResPost. When you change the version of FeResPost COM server, you have to modify the variable.
“storageMaxCapacity” is a “Double” variable that corresponds to the size in Megabytes of the buffer that stores information read from XDB attachments.
“maxNbrDataBases” contains the maximum number of databases that can be managed simultaneously by the excel project. Keeping the value low will reduce the use of memory by excel.
“maxNbrAttachments” corresponds to the maximum total number of attachments allowed in the project. Here again, the tuning of that value allows to reduce the amount of memory used by excel.
Also this module provides functions that allow to retrieve Results or load case information. Several such functions deserve more explanation:
“getCurrentDb” returns the currently active database corresponding to the currently selected load case name.
“getResults” is used to extract Results, or build them by calculating linear combinations.
“getParameter” is used to retrieve a parameter associated to the currently selected load case. (Arguments are the name of the currently selected load case, and the name of the parameter.)
These methods are mentioned here because they are used in “ExtractCriteria” module to program post-processing operations. The user that wishes to modify the post-processing criteria will use these functions.
Among other things, one defines in that module the different functions called in post-processing worksheets to perform specific post-processing operations. As this module defines many functions that can be called from post-processing worksheets, a separate section is specifically devoted to this module. (See section VII.4.4.)
The module defines the “extract” function that is used to extract values on selections of elements and nodes explicitly defined in the post-processing worksheet. This function is matricial as the different functions defined in “ExtractionCriteria” VBA module. The arguments of this function are:
A String corresponding to the type of entities on which the values are extracted. Possible values are “E” for elements, “N” for nodes or “EN” for pairs of elements and nodes.
A selection defining the list of entities on which the values are extracted. The values in the selection must be of integer type. The selection must have two columns if the first parameter is “EN”, one column otherwise.
The number of lines or the matrix returned by the function matches the number of lines of this selection.
A String corresponding to the name of the current load case.
A String corresponding to the type of Result that is requested.
A String or Integer corresponding to the layer on which values are extracted.
A String or Integer corresponding to the coordinate system in which the components are given.
A String corresponding to the name of the component that is requested. If this argument is “NONE”, all the components are returned.
The use of this function is illustrated in “post_extract” worksheet. So far the example worksheet only performs extraction operations without using the extracted values in post-processing.
The actual exploitation of extracted Results could be done directly by calculations in the excel worksheet. ‘ResultsExtraction” VBA module corresponds to a type of operation that is very often done in aeronautics. For example, when wings or fuselages are stressed, one often works with finite element models characterized by a structured numbering of elements and nodes that allow to easily extract shell forces or stresses for panels, beam forces for elements representing stringers or frames... This allows to estimate loads on rows of connections, assess the risk for a panel to buckle...
This module and the associated variables manage the archiving of Results. One of the module variables is a collection of arrays called “archiveList”. Each element in the collection contains the information necessary to archive one Result for later re-use:
One string corresponding to the name of worksheet in which the Results are saved.
One excel range of cells corresponding to the title inserted in the worksheet when it is created, i.e. when the worksheet is first accessed.
One excel range of cells corresponding to the values to be saved. (The number of columns in this range should preferably match the number of columns in the “title” selection.)
On excel range of cells corresponding to a test allowing to determine whether a selected line in the “values” range is to be archived. The check is done on a line-by-line basis. The number of lines in this range must match the number of lines in “values” range. The number of columns must be 1. (This argument has been added to avoid archiving some parts of the Results when necessary.)
The elements of each array correspond actually to the arguments of function “saveToArchive” used in post-processing worksheets. ‘saveToArchive” function returns a string that allows a check of the validity of arguments. It is the calculation of these functions that fills the “archiveList” collection in the module. This means that a recalculation of the worksheets must be performed before the archiving of Results. (By pressing “ArchiveResults” button in “LcSelector” worksheet for example). Also, the calculation of worksheets must be redone after pushing “ReinitArchiveResults” button in “LcSelector” worksheet. Indeed, the “ReinitArchiveResults” button clears the “archiveList” collection. This “clearing” operation may be useful to re-create the “archiveList” collection after a modification of the post-processing worksheets.
This module is used in the management of Results to be saved in GMSH files. To some extent, this module is similar to “ResultsArchiver” VBA module: it manages a outputsList module collection that contains the characteristics of Results to be saved, and the Results themselves.
One difference with “ResultsArchiver” VBA module is that the methods of “ResultsGmsh” are never called directly from the post-processing worksheets. Instead, methods from other VBA modules in the project call the methods of “ResultsGmsh”. For example, nearly all the methods of “ExtractionCriteria” module use “ResultsGmsh” to save envelope of Results in GMSH files. Indirectly, the user defines associated parameters in optional arguments of the post-processing functions defined in “ExtractionCriteria” module. (See section VII.4.4.)
The module defines several global variables:
“sqliteLibDirName” contains the path to the directory containing the “SQLite3” shared libraries. This variable must be adapted to match your installation.
“globOutputList” contains the envelopes of Results calculated for the current selection of load cases.
“locOutputList” contains the envelopes of Results for the current load case.
“sqlDbName” contains the name of the SQLite3 database in which Results are stored for each load case.
“sqlDbHandle” is a handle (pointer) to the current SQLite3 database.
Sqlite3 VBA module contains the VBA code devoted to the management of SQLite databases in Excel. This module is exactly the same as the one used in Small COM example 11. The reader is referred to section VII.1.9 for more information.
In this workbook, “Sqlite3” VBA module is used to generate a database containing for each load case the maximum stress or “failure indices”. These can be read a posteriori to save envelopes generated “manually” in GMSH files.
Note that the SQLite3 module is used by “ResultsGmsh” VBA module. This module generates all the SQLite3 operations, from the generation to the exploitation.
This module defines subroutines and functions that can be used from several different locations in the VBA project. For example:
“SheetExists” allows to check the presence of a worksheet in an excel workbook.
“checkItemExistsInCollection” allows to verify if a specified item exists in a collection.
“copyRangeFormat” copies several format characteristics of an excel range of cells to another range of cells. The sizes of the two ranges must match.
“setArrayAllValues” initializes all the values of an Array to the same specified value.
“clearAllModuleVariables” re-initializes the variables of several modules in the workbook.
“layersFromRange” returns an Array corresponding to a selection of Result layers. The argument of the function is an excel range (selection of cells).
These methods are called from several locations in the VBA module, but should never be used directly from an excel spreadsheet of the project.
The module defines several functions for extracting and manipulating Results. For example, the extraction of maximum Von Mises stress on a Group of elements, the calculation of honeycomb worst element and associated reserve factor, or the calculation of reserve factors for different connection criteria. One notes that:
These functions are called directly from the post-processing worksheets. These functions take a specified set of arguments and return an array of values (matricial functions). More precisely, so far, each extraction function returns a one line array of values. In order to know the number of columns, you should examine the examples or the sources of VBA module.
The functions return FALSE values in case of problem.
The definition of post-processing functions could be split in different post-processing VBA modules. This might be handy when many such functions are defined.
For all the post-processing criteria, the two last arguments of the associated functions are optional. These are string arguments corresponding to the name of a GMSH file in which an envelope of Results is stored, and the name of the Result that is saved in this GMSH output file. A majority of methods defined in “ExtractionCriteria” call methods in “ResultsGmsh” module to build the envelopes of Results.
(Generally, the envelopes that are calculated are the maximum of the inverse of reserve factors, but this is not an absolute rule.)
The module is the one that the user is most likely to modify to define new post-processing criteria. However, one advises those who wish to create their own criteria to define a new module called for example “UserCriteria” to develop their own functions.
Function “getVonMisesMax” in “ExtractionCriteria” VBA module extracts the maximum Von Mises equivalent stress on a Group of elements and on a selection of layers. The arguments of the function are:
A String corresponding to the name of the load case for which stresses are extracted.
A String corresponding to the location of extraction points on the elements. (For example: “Elements”, “ElemCenters” or “ElemCorners”.)
A selection of layers. This is a range of cells containing Integer or String values that are converted to a list of layers by “layersFromRange” method of “UTIL” VBA module.
A String corresponding to the Group of elements on which stresses are extracted.
Two optional String arguments corresponding to the name of the GMSH file in which the envelope of maximum equivalent stress shall be saved, and the name of the Result by which the Result is referred to in GMSH.
The function returns an Array of one line and six columns:
The element ID for maximum equivalent stress,
The node ID for maximum equivalent stress,
The layer ID for maximum equivalent stress,
The sub-layer ID for maximum equivalent stress,
The coordinate system ID which is always “NONE”,
The maximum Von Mises equivalent stress.
The use of “getVonMisesMax” is illustrated in “post_sandwich” spreadsheet.
Function “getShellVonMisesMax” in “ExtractionCriteria” VBA module extracts the maximum Shell Von Mises equivalent stress on a Group of elements and on a selection of layers. The arguments of the function are:
A String corresponding to the name of the load case for which stresses are extracted.
A String corresponding to the location of extraction points on the elements. (For example: “Elements”, “ElemCenters” or “ElemCorners”.)
A String corresponding to the Group of elements on which stresses are extracted.
Two optional String arguments corresponding to the name of the GMSH file in which the envelope of maximum equivalent stress shall be saved, and the name of the Result by which the Result is referred to in GMSH.
The function returns an Array of one line and six columns:
The element ID for maximum equivalent stress,
The node ID for maximum equivalent stress,
The layer ID for maximum equivalent stress,
The sub-layer ID for maximum equivalent stress,
The coordinate system ID which is always “NONE”,
The maximum Von Mises equivalent stress.
The difference between “getShellVonMisesMax” and “getVonMisesMax” is that one does not need to provide a selection of layers argument: the extraction is automatically done on layers “Z1” and “Z2”. The function returns a single value: the maximum Von Mises equivalent stress. The use of “getShellVonMisesMax” is illustrated in “post_sandwich” spreadsheet.
Function “getHoneycombCoreAirbusRF” in “ExtractionCriteria” VBA module calculates the minimum honeycomb reserve factor on a Group of elements using the so-called “Airbus” criterion:
|
|
in which and are the honeycomb longitudinal and transverse shear components of Cauchy stress tensor and and the corresponding allowables.
The arguments of the function are:
A String corresponding to the name of the load case for which Cauchy stress tensor is extracted.
A String corresponding to the location of extraction points on the elements. (For example: “Elements”, “ElemCenters” or “ElemCorners”.)
A String corresponding to the Group of elements on which stresses are extracted.
A String corresponding to the layer on which stresses are extracted.
A Real safety factor.
A Real value corresponding to the honeycomb longitudinal shear stress allowable .
A Real value corresponding to the honeycomb transverse shear stress allowable .
Two optional String arguments corresponding to the name of the GMSH file in which the envelope of maximum equivalent stress shall be saved, and the name of the Result by which the Result is referred to in GMSH.
The function returns an Array of one line and eight columns:
The element ID for minimum reserve factor,
The node ID for minimum reserve factor,
The layer ID for minimum reserve factor,
The sub-layer ID for minimum reserve factor,
The coordinate system ID for minimum reserve factor,
The value of longitudinal shear stress for minimum reserve factor,
The value of transverse shear stress for minimum reserve factor,
The minimum reserve factor.
The use of “getHoneycombCoreAirbusRF” is illustrated in “post_sandwich” spreadsheet.
Function “getHoneycombCoreMaxShearRF” in “ExtractionCriteria” VBA module calculates the minimum honeycomb reserve factor on a Group of elements using a maximum shear criterion:
|
|
in which is the maximum shear stress and the transverse shear allowable.
The arguments of the function are:
A String corresponding to the name of the load case for which Cauchy stress tensor is extracted.
A String corresponding to the location of extraction points on the elements. (For example: “Elements”, “ElemCenters” or “ElemCorners”.)
A String corresponding to the Group of elements on which stresses are extracted.
A String corresponding to the layer on which stresses are extracted.
A Real safety factor.
A Real value corresponding to the honeycomb longitudinal shear stress allowable . (This allowable is not used in the calculation.)
A Real value corresponding to the honeycomb transverse shear stress allowable . (Only this allowable is used in the calculation.)
Two optional String arguments corresponding to the name of the GMSH file in which the envelope of maximum equivalent stress shall be saved, and the name of the Result by which the Result is referred to in GMSH.
The function returns an Array of one line and eight columns:
The element ID for minimum reserve factor,
The node ID for minimum reserve factor,
The layer ID for minimum reserve factor,
The sub-layer ID for minimum reserve factor,
The coordinate system ID for minimum reserve factor,
The value of longitudinal shear stress for minimum reserve factor,
The value of transverse shear stress for minimum reserve factor,
The minimum reserve factor.
The use of “getHoneycombCoreMaxShearRF” is illustrated in “post_sandwich” spreadsheet.
For the post-processing of connection loads, the first step of the calculations is always to estimate for each connection the axial force, the shear force, the torsional moment and the bending moment. Afterwards the criterion for the connection is calculated (sliding, gapping, insert, rivet...). More precisely, one calculates the critical connection (node or element) and the associated reserve factor.
One explains here how the components of loading (axial and shear forces, torsional and bending moments) are first calculated for the different connections before the calculation of reserve factors for a selected criterion.
The parameters used for the calculation of these connection load components are always the first 6 parameters of the connection criterion function:
The name of the load case for which the calculation is done.
The name of a first Group (group1) corresponding generally to a part of the structure to which the connections are connected (sandwich panel, shell, metallic fitting...).
The name of second Group (group2) of finite element entities corresponding generally to the modeling of the connections (For example RBE2 elements, CBAR or CBUSH elements...).
A String corresponding to the type of operations done to build the different components of connection loads. This String determines which Results are first read from Result files, and how they are manipulated afterwards. More information about this parameter is given below.
An integer or String value corresponding to the coordinate system in which the force and moment vectors are to be expressed before extracting the different force and moment components.
A vector of three real values corresponding to the axis of the connection in the coordinate system given by the previous argument. The direction of this vector must be defined in such a way that a positive axial force corresponds to a tension in connection. For example, when internal forces are extracted from Grid Point Forces results, this is achieved by defining the vector pointing from grp2 to grp1 (to the direction of the group containing the elements from which Grid Point Forces are extracted.)
Presently, the available extraction methods for the load components, given by the fourth argument above are the following:
“GPFINT” if loads are obtained using Grid Point Forces, Internal Forces and Moments.
“GPFMPC” if loads are obtained using Grid Point Forces, MPC Forces and Moments.
“GPFSPC” if loads are obtained using Grid Point Forces, SPC Forces and Moments.
“MPCFRC” if loads are obtained from MPC Forces and Moments.
“SPCFRC” if loads are obtained from SPC Forces and Moments.
“BMFRC” is loads are obtained from Beam Forces and Moments. (This may correspond to forces of several elements like CBAR, CBEAM, CBUSH or CFAST.)
When the option “BMFRC” is adopted, the loads are extracted on the “beam-type” elements modeling the connections (CBUSH elements for example). This means that the only the second Group argument (third argument of the function) matters. The first Group argument is not considered. In all other cases, Group operations are done to obtain a list of nodes which is the intersection of the two Group arguments provided. More precisely, the Group “targetGrp” is build as follows:
If extractionMethod = "BMFRC" Then Set targetGrp = grp2 Else Set nodeGrp1 = db.getNodesAssociatedToRbes(grp1) Set tmpGrp1 = db.getNodesAssociatedToElements(grp1) nodeGrp1.importEntitiesByType "Node", tmpGrp1 Set nodeGrp2 = db.getNodesAssociatedToRbes(grp2) Set tmpGrp2 = db.getNodesAssociatedToElements(grp2) nodeGrp2.importEntitiesByType "Node", tmpGrp2 Set tmpGrp3 = nodeGrp1.opMul(nodeGrp2) Set tmpGrp2 = db.getElementsAssociatedToNodes(tmpGrp3) Set tmpGrp1 = grp1.opMul(tmpGrp2) Set targetGrp = tmpGrp1.opAdd(tmpGrp3) End If
Depending on the type of extraction, and on specific aspects of the problem, the correspondence between grp1 and grp2 on one side and the connections or assembled part may differ. For example:
When MPC or SPC forces and moments are post-processed. The choice of grp1 and grp2 is indifferent as loads are extracted on the intersection nodes only.
When one processes Grid Point Forces internal forces and moments, the definition of grp1 and grp2 may matter. Consider the example represented in Figure VII.4.1 in which Part 2 is a sandwich panel modeled with shell elements. Then,
If one calculates inserts margins of safety, loads should be extracted on elements of sandwich panel at connection nodes because the inserts of sandwich panels are loaded by connections of Groups “ConnectGrp2” and “ConnectGrp3”. This means the grp1 should correspond to Part 2 and grp2 to either “ConnectGrp2” and “ConnectGrp3”.
On the other hand, if one calculates sliding between Part 1 and Part 2, only the loads transmitted by elements of Group “ConnectGrp2” must be recovered. Then grp1 should correspond to Group “ConnectGrp2” and grp2 to Part2. Of course, this will work only if the connections are modeled with elements (CBUSH, CBAR,...) and not MPCs or rigid body elements (RBEs).
In many cases, grp1 and grp2 can be switched without consequences on the results. Then it is generally less expensive to select grp1 corresponding to the Group containing the connections.
Note however that when grp1 and grp2 are switched, the vector defining axial direction should be reversed too!
All the operations are managed by subroutine “getConnectionLoads” of “ExtractionCriteria” VBA module. This subroutine is called by each of the connection post-processing function. This is why the six parameters (eight values) of these connection post-processing functions are always the same.
This function calculates reserve factors for the sliding criterion with the following expression:
|
|
in which is the friction coefficient between assembled elements and is an estimate of the minimum possible pretension of the bolt. Parameters specific to this function are:
The factor of safety “FoS”. (Parameter 7 of the function.)
The minimum estimated pretension of a connection “Pmin”. (Parameter 8 of the function.)
The friction coefficient “Cf”. (Parameter 9 of the function.)
Two optional parameters containing the name of the GMSH file in which the envelope of inverse reserve factors is saved, and the name of the Result by which it is referred to in the GMSH file.
The function returns an Array of one line and four columns containing:
The ID of the finite element entity to which minimum reserve factor corresponds. This is the ID of an element for “BMFRC” extraction and a node ID otherwise.
The corresponding axial force.
The corresponding shear force.
The minimum reserve factor.
This function calculates reserve factors for the gapping criterion with the following expression:
|
|
in which is a parameter that allows to take into account the prying effect related to the bending moment in the connection and is an estimate of the minimum possible pretension of the bolt. Parameters specific to this function are:
The factor of safety “FoS”. (Parameter 7 of the function.)
The minimum estimated pretension of a connection “Pmin”. (Parameter 8 of the function.)
The friction coefficient “Radius”. (Parameter 9 of the function.)
Two optional parameters containing the name of the GMSH file in which the envelope of inverse reserve factors is saved, and the name of the Result by which it is referred to in the GMSH file.
The function returns an Array of one line and four columns containing:
The ID of the finite element entity to which minimum reserve factor corresponds. This is the ID of an element for “BMFRC” extraction and a node ID otherwise.
The corresponding axial force.
The corresponding bending moment.
The minimum reserve factor.
This function calculates reserve factors for the insert criterion with the following expression:
|
|
In which “PSS” is the axial allowable of the insert and “QSS” is its shear allowable. Parameters specific to this function are:
The factor of safety “FoS”. (Parameter 7 of the function.)
The insert axial allowable “PSS”. (Parameter 8 of the function.)
The insert shear allowable “QSS”. (Parameter 9 of the function.)
Two optional parameters containing the name of the GMSH file in which the envelope of inverse reserve factors is saved, and the name of the Result by which it is referred to in the GMSH file.
The function returns an Array of one line and four columns containing:
The ID of the finite element entity to which minimum reserve factor corresponds. This is the ID of an element for “BMFRC” extraction and a node ID otherwise.
The corresponding axial force.
The corresponding shear force.
The minimum reserve factor.
This function calculates reserve factors for the shear-bearing failure mode with the following expression:
|
|
in which is the shear bearing allowable. Parameters specific to this function are:
The factor of safety “FoS”. (Parameter 7 of the function.)
The shear-bearing allowable “ShrAll”. (Parameter 8 of the function.)
Two optional parameters containing the name of the GMSH file in which the envelope of inverse reserve factors is saved, and the name of the Result by which it is referred to in the GMSH file.
The function returns an Array of one line and three columns containing:
The ID of the finite element entity to which minimum reserve factor corresponds. This is the ID of an element for “BMFRC” extraction and a node ID otherwise.
The corresponding shear force.
The minimum reserve factor.
This function calculates reserve factors for the pull-through failure mode with the following expression:
|
|
in which is the pull-through tensile allowable. Parameters specific to this function are:
The factor of safety “FoS”. (Parameter 7 of the function.)
The pull-through allowable “PullAll”. (Parameter 8 of the function.)
Two optional parameters containing the name of the GMSH file in which the envelope of inverse reserve factors is saved, and the name of the Result by which it is referred to in the GMSH file.
The function returns an Array of one line and three columns containing:
The ID of the finite element entity to which minimum reserve factor corresponds. This is the ID of an element for “BMFRC” extraction and a node ID otherwise.
The corresponding axial force.
The minimum reserve factor.
Function “getCompositeRF” of “ExtractionCriteria” VBA module calculates reserve factors using the classical laminate analysis. More precisely, the Shell Forces and Moments are recovered on shell elements with laminated properties (PCOMP or PCOMPG properties), and the layered reserve factors are calculated using “calcFiniteElementResponse” method of the generic Database class. Note however that one limitation of this post-processing function is that no thermo-elastic or hygro-elastic contribution is taken into account in the post-processing. Reserve factors are generally calculated at mid thickness of each layer. One exception is the inter-laminar shear stress reserve factor which is calculated at bottom sub-layer of the selected plies.
Function “getCompositeRF” has the following arguments:
The name of the load case for which the calculation is done.
The location(s) in elements of the points at which reserve factors will be calculated. (For example “ElemCenters” or “ElemCorners”.)
The name of a Group on which the reserve factors are calculated.
The name of the failure criterion for which reserve factors are calculated. (The list of available criteria is summarized in Table II.1.2.)
A selection of cells containing the list of layers on which the composite criterion is to be estimated.
The factor of safety.
Two optional String arguments corresponding to the name of the GMSH file in which the envelope of inverse reserve factors shall be saved, and the name of the Result by which the Result is referred to in GMSH.
The function returns an Array of one line and five columns containing:
The element ID for minimum reserve factor.
The node ID for minimum reserve factor.
The layer ID for minimum reserve factor.
The sub-layer ID for minimum reserve factor.
The minimum reserve factor.
The use of “getCompositeRF” function is illustrated in “post_composite” worksheet.
“getCompositeRF2” function defined in “UserCriteria” Module is a variant of “getCompositeRF” with two additional arguments:
“bCurvature” is a boolean that specifies that one loads the laminates with “Curvature Tensor” instead of “Shell Moments Tensor” to calculate laminate load response. item “tempFieldId” corresponds to an integer that allows to retrieve a temperature field from “sqliteResults.db3” database to load the laminate. This contribution is taken into account if the database is located in excel working directory, and if the specified temperature field is found in the database. In the example, the “TempLoad” parameter is used to associate the temperature fields to post-processing load case.
Note that one explains in section IV.2.8.5 how the SQLite database containing the temperature Results can be produced.
“getCompositeRF3” function defined in “UserCriteria” Module is a variant of “getCompositeRF” that calculates laminate failure criteria directly from the stresses extracted from finite element model results. This function has been used to test the different variants of the functions calculating laminate criteria. The arguments of this function are the same as those of “getCompositeRF” function.
On Windows OS, FeResPost is distributed at the same time as a ruby extension, a COM component and as a .NET assembly. One describes in this Part several characteristics of FeResPost as a .NET assembly.
In general, the class names, their methods and attributes (properties), the parameters of these methods and attributes are the same as those available in the FeResPost ruby extension. When necessary, modifications have been done in the ruby extension in order to maintain as much as possible the compatibility between the ruby extension and the .NET assembly. Therefore, the user is referred to Parts I, II, III and IV to find information on the use of the different classes and methods. In most cases, the information given there is sufficient to use the .NET assembly.
However, an exact match between the ruby extension and .NET assembly is not possible. One details below the conventions that have been adopted when incompatibility problems were not solved. More generally, one explains here the specific aspects of the use of FeResPost as a .NET assembly.
This Part of the document is organized as follows:
Chapter VIII.2 presents the .NET characteristics of the FeResPost generic classes described in Part I.
Chapter VIII.1 presents the .NET characteristics of the FeResPost CLA classes described in Part II.
Chapter VIII.3 presents the .NET characteristics of the FeResPost generic classes described in Part III. (Solver classes.)
In Chapter IX.1, one gives a few examples illustrating the use of FeResPost .NET assembly.
The installation of the .NET assembly is described in section X.A.4.6.
In the different sections of this chapter, one describes conventions that have been adopted when translating the ruby extension into a .NET assembly. Information is given each time the ruby methods are modified to be implemented into the .NET assembly. For example, this is done for iterators, operators, “clone” method... Also one explains how objects are created with the assembly.
One highlights below some differences between .NET assembly and ruby extension that are related to specific programmatic aspects of the two different systems.
If FeResPost assembly is installed into global assembly cache, no peculiar operation is necessary to access it from IronRuby. If FeResPost is not installed in global assembly cache, a path must be provided to IronRuby to retrieve the library. This is done, for example, with the “-I” option.
When compiling a C# program, the library must be referenced at compile-time with the “-r” option. For example:
csc.exe -r:../../../SRC/OUTPUTS/NET/FeResPost.dll ...
This referencing must be done, even if the library is installed in global assembly cache. Note however, that after compiling the C# client program, this program can be moved elsewhere independently of the FeResPost assembly, if this assembly has been installed in Global Assembly Cache.
We assume that was is true for IronRuby, shall be true for other .NET interpreted languages as well. Similarly, what is true for C# compiled programs is applicable for other CLI compiled languages (C++/CLI or VB/CLI).
All classes of the FeResPost .NET assembly are defined in “FeResPost” namespace. To simplify the access to FeResPost classes and methods, it is recommended to give access to the content of the namespace.
In ruby, this is done by including FeResPost Module into the current workspace:
... include FeResPost ...
In C#, one uses using directives:
... using FeResPost ; ...
The same is true for C++.NET language, but with a different syntax:
... using namespace FeResPost ; ...
The creation of FeResPost objects depends on the language with which .NET assembly is used. In all cases, the “new” operator is used. For example to create a ClaDb object in ruby, one writes:
... db=ClaDb.new ...
The same operation is done as follows in C#:
... ClaDb db; db=new ClaDb(); ...
(Note that the variable db has been declared before being initialized.)
In FeResPost .NET assembly, the following default types are used for parameters:
Real are single precision real values corresponding to “float” C++/CLI type or “Single” CLR type. Note however, that “double” arguments are sometimes accepted.
Integer values are 32 bits integers corresponding to “int” C++/CLI type or “Int32” CLR type.
Logical values correspond to “bool” C++/CLI type or “Boolean” CLR type.
Strings of characters are passed as “String” C++/CLR/CLI objects.
...
The different classes defined in FeResPost assembly are reference managed classes. The examples given in Part IX should clarify the use of arguments.
When methods of ruby extension receive or return Array objects, .NET assembly also returns Arrays of different types of objects. The difference is that .NET Arrays may have several dimensions. For example, the C++/CLI definition of several methods of the ClaLam class reads as follows:
... array<float,2>^ get_ABBD(...array<float>^ varargs) ; array<float,2>^ get_G(...array<float>^ varargs) ; array<float>^ get_alfaEh1(...array<float>^ varargs) ; ...
The two first methods above return 2D arrays, instead of 1D arrays of 1D arrays, for ruby extension.
Similarly, when a FeResPost method of ruby extension receives or returns a Hash object, the corresponding method of .NET assembly deal with a Dictionary. For examples, the methods of CLA classes devoted to management of units are declared as follows:
... System::Collections::Generic::Dictionary<System::String^, System::String^>^ getUnits(void) ; void setUnits(System::Collections::Generic::Dictionary< System::String^,System::String^>^ Units) ; void changeUnits(System::Collections::Generic::Dictionary< System::String^,System::String^>^ Units) ; ...
.NET provides a standard interface that allows the writing of iterators on collections of different types. In FeResPost, all the iterators are based on two classes:
The “Iterator” class that implements “IEnumerable” interface.
The “IterX” class that implements “IEnumerator” interface.
As for the COM component, two classes devoted to iterations have been added because it does not seem possible to create a class that proposes several enumerators.
The “Iterator” class is common to all the iterators of all the FeResPost classes. But an Iterator object behaves differently depending on the class that produces it and/or the method of the class that is used to produce it.
Let us illustrate it by an example... Consider the “each_ply” iterator defined in ClaLam class of FeResPost ruby extension. With the ruby extension, the iteration on the plies of a laminate may be performed as follows:
... lam.each_ply do |plyDescr| ... end ...
With FeResPost .NET assembly and IronRuby, an Iterator must first be produced before iterating on the elements of the corresponding collection. This can be done as follows:
... plyIt = lam.iter_ply plyIt.each do |plyDescr| ... end ...
This examples illustrates the conventions that have been used when programming the FeResPost .NET assembly to transpose the iterators proposed in the ruby extension:
As in the FeResPost ruby extension, each iterator method name starts with “each_”, correspondingly, the .NET assembly methods returning an Iterator object have a name that starts with “iter_”. The correspondence between ruby extension methods and .NET assembly methods is obvious: “each_ply” becomes “iter_ply”, “each_material” becomes “iter_material”,...
When the .NET iteration method has no argument, it is a property “getter” that is used instead of a method. Otherwise, a method with argument is defined.
In IronRuby using the .NET assembly, the iteration on the Iterator object is done using “each” iteration method.
Note that to the IronRuby lines given as example above, one prefers the shorter notation:
... lam.iter_ply.each do |plyDescr| ... end ...
Operators are defined in the different classes to which they apply (Group, Result, ResKeyList...). Note that C++/CLI allows to define in managed classes static operators the first operand of which is an object that is not an instantiation of the class. This allows, for example, to define dyadic operators the first operand of which is a float, and the second operand of which a Result object.
Ruby “singleton” methods of FeResPost classes are defined as static functions of FeResPost managed classes.
Most FeResPost managed classes implement the “ICloneable” interface and define a “Clone” method that corresponds to ruby “clone” method in FeResPost ruby extension. “Post” static class does not derive from ICloneable, as this class can not be instantiated. Also, the classes deriving from “DataBase” (“NastranDb” and “SamcefDb” classes) do not implement the “Clone” method.
The “to_s” method of ruby extension are replaced by “ToString” method in .NET assembly.
FeResPost does not define Modules. The ruby extension “Post” Module is replaced a static “Post” class in .NET assembly. More precisely, “Post” class defines only static methods and no constructor/destructor.
All the methods defined in “Post” module of ruby extension are defined in “Post” static class.
Complex arguments are input as 1D Arrays of two float or double values.
.NET assembly defines a “FrpExcept” class corresponding to all the exceptions raised by FeResPost. The management of exceptions is as with ruby, but is also depends on the programming language. For example, with C#, the management of an exception may look like:
try {
NastranDb db=new NastranDb();
db.Name="tmpDB1";
//~ db.readBdf("../../MODEL/MAINS/unit_xyz.bdf");
db.readBdf("../../MODEL/MAINS/brol.bdf");
}
catch (FrpExcept ex) {
Console.WriteLine("\n\nGot an exception of type \"{0}\"\n",ex.GetType());
Console.WriteLine("FeResPost error message is :\n\n{0}\n",ex.Message);
}
In general, the selection of output stream for the writing of FeResPost information messages follows the same rules as for ruby extension, as explained in section I.6.1. The default output stream for information messages is “System.IO.Console.Out”. Method “setInfoStreamToClientStream” accepts as argument anyclass that derives from “System.IO.Console.TextWriter” class. Valid arguments are for example a TextWriter object, a StreamWriter object, System.IO.Console.Out, System.IO.Console.Error...
The different classes described in this Chapter correspond to the classes described in Part II. The methods defined in FeResPost .NET assembly CLA classes are the same as those defined in the FeResPost ruby extension CLA classes, except the peculiar problem of the iterators discussed in section VIII.0.6, and of the “clone” methods that have been replaced by “makeCopy” methods.
Similarly, the arguments defined for the different methods of CLA classes are the same as those for the classes of FeResPost ruby extension, except for the remark done in section VIII.0.5 for the “Hash” arguments or returned values.
In the rest of this Chapter, one makes a few remarks about the different classes. But otherwise, the reader is referred to the different chapters of Part II to find information on the use of .NET assembly CLA classes.
No peculiar remark is to be done except for the iterators:
Iterator “each_material” in ruby extension becomes “iter_material”.
Iterator “each_materialId” in ruby extension becomes “iter_materialId”.
Iterator “each_laminate” in ruby extension becomes “iter_laminate”.
Iterator “each_laminateId” in ruby extension becomes “iter_laminteId”.
Iterator “each_load” in ruby extension becomes “iter_load”.
Iterator “each_loadId” in ruby extension becomes “iter_loadId”.
The “Clone” method that returns a copy of the object.
Methods returning a 2D matrix, return a an Array with 2 dimensions. These methods are “getCompliance”, “getStiffness”, “getInPlaneCompliance”, “getInPlaneStiffness”, “getOOPSCompliance”, “getOOPSStiffness”, “getInPlaneLambdaT”, “getInPlaneLambdaH”. (In ruby extension, these methods return an array of arrays.)
The “Clone” method that returns a copy of the object.
Iterator “each_ply” in ruby extension becomes “iter_ply”.
Methods returning a 2D matrix, return a an Array with 2 dimensions. These methods are “get_ABBD”, “get_G”, “get_abbd_complMat”, “get_g_complMat”, “get_LambdaT”, “get_LambdaH”. (In ruby extension, these methods return an array of arrays.)
Methods that return Ply stresses, strains, temperature or moisture return 2D Arrays of size N*8 or N*3.
The “getDerived”, “getFailureIndices” and “getReserveFactors” methods return Arrays of 2 objects. The second object is a 2D Array in .NET assembly.
Methods “getMaxDerived”, “getMinDerived”, “getMaxFailureIndices”, “getMinFailureIndices”, “getMaxReserveFactors” and “getMinReserveFactors” returns 2 dimensional Arrays of sizes N*3.
The “Clone” method that returns a copy of the object.
No peculiar remark is to be done. The “Clone” method that returns a copy of the object.
Most classes defined in this chapter correspond to the same classes in ruby extension.
The two classes “Iterator” and “IterX” correspond to the iterators defined in the different classes of the NET assembly. These classes are not described in this chapter. Indeed, one considers that the explanations given in section VI.0.2.3 for COM component iterators about the use of iterators is sufficient. No corresponding class exists in the ruby extension.
The “Post” static class corresponds to Presently, these methods are
The methods “openMsgOutputFile”, “closeMsgOutputFile” and “writeAboutInformation”.
The methods “readGroupsFromPatranSession” and “writeGroupsToPatranSession” to read lists of Groups in Arrays.
Several methods for the manipulation of Results like “cmp”, “max”, “sin”, “sq”, “exp”,...
The “convertBlob” method deals with Array of Bytes (unsigned char) instead of Strings in the ruby extension.
...
Note that no dyadic “operator” “op*” is defined in “Post” class, as was done in COM component or ruby extension. Instead, these operators are defined as static operators in the “Result”, “Group” and “ResKeyList” classes
This class corresponds to the generic DataBase class of ruby described in Chapter I.1. The class cannot be instantiated; instead, the corresponding specialized classes “NastranDb” and “SamcefDb” that derive from DataBase can be instantiated.
The iterators of the DataBase class in ruby extension have also been defined in COM
component: “iter_abbreviation”, “iter_groupName”, “iter_resultKey”, “iter_resultKeyCaseId”,
“iter_resultKeySubCaseId”, “iter_resultKeyLcScId” and ‘iter_resultKeyResId” properties in COM
component correspond to the “each_abbreviation”, “each_groupName”, “each_resultKey”,
“each_resultKeyCaseId”, “each_resultKeySubCaseId”, “each_resultKeyLcScId” and
“each_resultKeyResId” iterators in ruby extension.
The four singleton methods “enableLayeredResultsReading”, “disableLayeredResultsReading”, “enableSubLayersReading” and “disableSubLayersReading” in the ruby extension generic DataBase class are defined as static methods in NET assembly. No instance of the derived class must be created to use these singleton methods.
Similarly, methods“setStorageBufferMaxCapacity” and “getStorageBufferMaxCapacity” are defined as static methods in DataBase class.
Most methods of the “Group” class are exactly the same as the ones defined in the Group class of ruby extension (Chapter I.3). Several methods or properties are different however:
The iterators are now “iter_element”, “iter_rbe”, “iter_node” and “iter_coordsys” instead of “each_element”, “each_rbe”, “each_node” and “each_coordsys”.
The “toBlob” and “fromBlob” methods deal with Array of Bytes (unsigned char) instead of Strings in the ruby extension.
The “Clone” method that returns a copy of the object.
Methods of the “CoordSys” class are the same as the ones defined in the CoordSys class in ruby extension. The “Clone” method that returns a copy of the object.
Most methods of the “Result” class are exactly the same as the ones defined in the Result class in ruby extension (Chapter I.4). Several methods or properties are different however:
The iterators are now “iter”, “iter_key” and “iter_values”.
The “getData” method returns a 2D Array, instead of an array of arrays as in the ruby extension.
Several operators defined as “static” in Result class allow to have a float first argument for corresponding dyadic operations.
The “toBlob” and “fromBlob” methods deal with Array of Bytes (unsigned char) instead of Strings in the ruby extension.
The “Clone” method that returns a copy of the object.
Methods of the “ResKeyList” class are the same as the ones defined in the ResKeyList class in ruby extension. However:
The property “each_key” is here named “iter_key”.
The “getData” method returns a 2D Array, instead of an array of arrays as in the ruby extension.
The “Clone” method returns a copy of the object.
The two classes that correspond to the two supported solvers (Nastran and Samcef) are complete.
The “NastranDb” class stores a model and results corresponds to Nastran finite element solver. Methods specific to the NET assembly are:
The “makeCopy” method that returns a copy of the database.
Several iterator methods with or without argument: “iter_coordSysId”, “iter_elemId”, “iter_nodeId”, “iter_rbeId”, “iter_materialId”, “iter_propertyId”, “iter_nodeOfElement”, “iter_cornerNodeOfElement”. When these iterators have arguments, they are implemented with methods and not with properties.
The reader is referred to Chapter III.1 for the description of the other methods.
The “SamcefDb” class stores a model and results corresponds to Samcef finite element solver. The other methods that are available are:
The “makeCopy” method that returns a copy of the database.
Several iterator methods with or without argument: “iter_coordSysId”, “iter_elemId”,
“iter_nodeId”, “iter_materialId”, “iter_samcefPlyId”, “iter_samcefLaminateId”,
“iter_samcefMatIdName”, “iter_samcefMatNameId”, “iter_nodeOfElement”,
“iter_cornerNodeOfElement”. When these iterators have arguments, they are
implemented with methods and not with properties.
The reader is referred to Chapter III.2 for the description of the other methods.
Presently, the examples of usage for the .NET assembly are limited mostly to C# language examples. These examples are provided in sub-directories of “TESTSAT/NETEX” and correspond to the small examples “TESTSAT/RUBY” of FeResPost ruby extension discussed in chapter IV.2.
In this chapter, one highlights the differences between ruby extension and .NET assembly. For that reason, only a few examples are discussed. For the other examples, the discussion of corresponding ruby examples in chapter IV.2 and refexamples.CLA.chap should be sufficient.
The first C# example is very simple and illustrates the use of .NET assembly with C# programming language. The example is provided in “TESTSAT/NETEX/EX01/readBdf.cs” source file. The compilation is done with script “readBdf.bat” that contains the following lines:
@SET FRP=../../../SRC/OUTPUTS/NET C:/Windows/Microsoft.NET/Framework/v3.5/csc.exe -platform:x86 \ -r:%FRP%/FeResPost.dll ..\UTIL\util.cs readBdf.cs readBdf.exe
(You may have to change the “%FRP%” path to FeResPost .NET assembly before compiling the example.) Note also that one uses the 3.5 version of .NET Framework. This is not strictly necessary in this example, but it might be useful for some examples in which classes are extended with extension methods. Once the compilation is done, the compiled program is run by line “readBdf.exe”.
The file “readBdf.cs” begins with several “using” directives:
using System; using System.Collections; using System.Collections.Generic; using System.Text; using System.Globalization; using System.Threading; using FeResPost ; using std ;
These directives allow to reduce the length of type names used in the program. For example, the “using FeResPost” directive allows to use “NastranDb” keyword instead of “FeResPost.NastranDb”.
The first example is very simple and contains only one static “Main” function:
namespace ConsoleApplication1 {
class readBdf {
static void Main(string[] args) {
...
} // static void Main(string[] args)
} // class readBdf
} // namespace ConsoleApplication1
Note however, that the static function is contained in a class. (C# does not allow to define a function outside of a class.) The “readBdf” class is also contained in a “ConsoleApplication1” namespace.
The other lines defining the program are very simple and considered as “classical” C# programming:
NastranDb db = new NastranDb();
db.Name="tmpDB1";
db.readBdf("../../MODEL/MAINS/unit_xyz.bdf");
// A Second DataBase is created :
db = new NastranDb();
db.Name="tmpDB2";
db.readBdf("unit_xyz_V1.bdf","../../MODEL/MESH/","bdf",
new Dictionary<string,string>(),true);
(The reader is referred to chapter III.1 for the description of “readBdf” arguments.) Note that in the second call to “readBdf”, one uses a void “Dictionary” instead of a ruby “Hash” object as parameter.
One presents in “readBdf_V2.cs” and “readBdf_V3.cs” variants on of this first example.
“readBdf_V2_rb.rb” contains an IronRuby version of C# example “readBdf_V2.cs”. The first call to “readBdf is done as follows:
...
bdfName=System::String.new("unit_xyz_V2.bdf")
symbols=Hash.new
symbols["INCDIR"]="../../MODEL"
db=NastranDb.new()
db.Name="tmpDB2"
begin
db.readBdf(bdfName,[],System.String("bdf"),symbols,true)
rescue Exception => x then
...
Of course, this call fails because ruby standard Arrays or Hashes cannot be used as CLI Arrays or dictionaries. Instead, the following statements work:
...
symbols=System::Collections::Generic::Dictionary[System::String,System::String].new
symbols.Add("INCDIR","../../MODEL");
db.readBdf(bdfName,System::Array[System::String].new(0),System::String.new("bdf"),symbols,true)
...
The example illustrates the difficulty of marshaling CLI data types with IronRuby. We expect this to be true for all interpreted languages.
The example is provided in “TESTSAT/NETEX/EX05/printStressMax.cs” source file. This example is worth discussing because it illustrates the difference between the value returned by “Result.getData” method in ruby extension and in C#.
In the example, one extracts the data on a Result which associates only one key-value pair, but the present principles are valid for more general Results. The following ruby lines make use of the ruby extension and extract and print the stress components :
...
maxScalarData = maxScalar.getData()[0]
maxStressData = maxStress.getData()[0]
...
printf(" %.2f Pa on element %d (layer=\"%s\").\n",
maxScalarData[5],maxScalarData[0],maxScalarData[2])
printf(" Sxx = %.2f, Syy = %.2f, Szz = %.2f,\n",maxStressData[5],\
maxStressData[6],maxStressData[7])
printf(" Sxy = %.2f, Syz = %.2f, Szx = %.2f\n",maxStressData[8],\
maxStressData[9],maxStressData[10])
...
The same operation is performed with .NET assembly by the following C# code:
...
maxScalarData=maxScalar.getData();
maxStressData=maxStress.getData();
Console.WriteLine();
Console.WriteLine("Maximum Von Mises stress in panel +Z skins :");
Console.WriteLine();
Console.Write(" {0:F2} Pa ",maxScalarData[0,5]);
Console.Write("on element {0:D} ",maxScalarData[0,0]);
Console.WriteLine("(layer=\"{0:S}\")",maxScalarData[0,2]);
Console.Write(" Sxx = {0:F2}, ",maxStressData[0,5]);
Console.Write("Syy = {0:F2}, ",maxStressData[0,6]);
Console.WriteLine("Szz = {0:F2}, ",maxStressData[0,7]);
Console.Write(" Sxy = {0:F2}, ",maxStressData[0,8]);
Console.Write("Syz = {0:F2}, ",maxStressData[0,9]);
Console.WriteLine("Szx = {0:F2} ",maxStressData[0,10]);
...
One notices that one no longer accesses element 0 of the array returned by “getData”. Indeed, in .NET assembly, the method returns a 2D Array, and not an Array of Arrays as in ruby extension.
In the “NETEX/EX02/properties.cs” example, one shows how one can access the properties in the finite element model. The C# code looks as follows:
object[] card;
foreach (int pid in db.iter_propertyId()) {
os.Write("{0,8}",pid);
os.Write("\n\n");
card=db.fillCard("Property",pid);
os.Write("{0,8}",card[0]);
for (int i=1;i<card.Length;i++) {
os.Write("{0,8}",card[i]);
if (i%8==0&&i!=card.Length-1) {
os.Write("\n");
os.Write("{0,8}","");
}
}
os.Write("\n\n");
}
This example illustrates the use of “fillCard” method, already presented in sections III.1.1.5 and IV.2.3
The examples provided in “NETEX/EX13” illustrate the possibility to extend FeResPost classes in C# by defining “extension” methods. Note however that this capability exists only if a version 3 or above of the C# compiler is used.
In the following example, extracted from “NETEX/EX13/extendedCla.cs”, The ClaMat class is extended with method “write_Compliance”:
namespace extension {
static class ext {
...
public static void write_Compliance(this ClaMat m,
StreamWriter os,float theta) {
writeMat(os,m.getCompliance(theta));
}
...
Note that the first argument is “this ClaMat m”, which indicates the class that is being extended. In file “NETEX/EX13/extendedCla.cs”, the extension methods are defined in “extension” namespace. A “using extension” statement must be present in the client program to access the extensions.
Note also, that many of the methods defined in C# differ from the ruby corresponding ruby methods with ruby extension. For example, the following C# source lines take into account that “getPliesStresses” method of .NET assembly returns a 2D Array:
...
sigTab=l.getPliesStresses();
nbrLines=sigTab.GetLength(0);
os.Write(" {0,8}{1,5}","layer","loc");
os.Write("{0,14}{1,14}{2,14}","sig_11","sig_22","sig_12");
os.Write("\n");
for (i=0;i<nbrLines;i++) {
os.Write(" {0,8}{1,5}",sigTab[i,0],sigTab[i,1]);
os.WriteLine("{0,14}{1,14}{2,14}",sigTab[i,2],
sigTab[i,3],sigTab[i,7]);
}
os.Write("\n");
...
Ruby extension returns an Array of Arrays and the corresponding lines would be:
...
sigTab=getPliesStresses
os.printf(" %8s%5s","layer","loc")
os.printf("%14s%14s%14s","sig_11","sig_22","sig_12")
os.printf("\n")
(0...sigTab.size).each do |i|
os.printf(" %8d%5s",sigTab[i][0],sigTab[i][1])
os.printf("%14g%14g%14g",sigTab[i][2],sigTab[i][3],
sigTab[i][7])
os.printf("\n")
end
...
This example is presented in files “rehashDynamicResults.cs” and “deleteSomeResults.cs” of directory “TESTSAT/NETEX/EX20” correspond exactly to the ruby examples of section IV.2.6.
The access to SQLite .NET assembly, which must be installed on the computer is done by the following statement:
using System.Data.SQLite ;
Note also the binding of parameters to SQLite command:
cmd.CommandText = sql;
cmd.Parameters.Clear();
cmd.Parameters.AddWithValue("@lcName", id[0]);
cmd.Parameters.AddWithValue("@scName", id[1]);
cmd.Parameters.AddWithValue("@resName", id[2]);
cmd.Parameters.AddWithValue("@tensorOrder", tensorOrder);
cmd.Parameters.AddWithValue("@intId1", intId1);
cmd.Parameters.AddWithValue("@intId2", intId2);
cmd.Parameters.AddWithValue("@realId1", realId1);
cmd.Parameters.AddWithValue("@realId2", realId2);
cmd.Parameters.AddWithValue("@size", size);
cmd.Parameters.AddWithValue("@result", resBlob);
cmd.ExecuteNonQuery();
The NET examples in directory “TESTSAT/PYTHON/EX27” are a simple translation of the ruby example discussed in section IV.2.11. Example are written with C#.
FeResPost is open source. Both the C/C++ sources and binaries are distributed.
The binaries are distributed in archive containing the “OUTPUTS” directory and its sub-directories. These binaries can also be re-generated from the sources as described in section X.A.1.
Depending on the OS and on the type of the binaries you are using, part of the distribution is to be used.
File “OUTPUTS/COMPILER.TXT” contains information about the compiler that has been used to produce the binaries. File “build.log” contains additional information on the build environment.
Note that the C++ shared libraries are still distributed in “OUTPUTS/lib” directory to maintain compatibility with what was done with previous versions. The use of these binaries is however not recommended because:
The methods of the shared library throw C++ exceptions. This may lead to problems at the interfaces of shared objects.
The compatibility of shared objects built from C++ code depends on the compiler used to produce them (or on its version). You might be unable to use the distributed libraries.
If you intend to develop your own wrappers or use FeResPost classes in your own programs we recommend that you recompile FeResPost C++ library with you own compiler, and statically link your executables/libraries to FeResPost objects.
Table X.A.1 gives an idea of successful build, in particular of the different versions of ruby and Python for which FeResPost library has been compiled. Note however, that the success of failure of a compilation may depend on compiler version and that the list can change. The best way to check the availability of compiled library for a given version is to explore the corresponding archives.
In archive “FeResPost_5.0.9_LINUX_32.7z” the binaries contain ruby wrappers and C++ library:
“OUTPUTS/lib” directory contains the file “libFeResPost_5.0.9.so” that corresponds to the FeResPost C++ library without any wrapper. If you intend to work with the C++ shared library, this file should be located in a library standard directory, or in a library pointed to by environment variable “LD_LIBRARY_PATH”.
“OUTPUTS/include” directory and its subdirectories contain FeResPost C++ headers. You have no use of these files unless you wish to develop your own wrapper for FeResPost (for use with Python, Perl, Java...), or use FeResPost C++ library in one of your C++ applications. So most of you can forget this directory.
“OUTPUTS/RUBY/” directory contains RUBY extensions (in different sub-directories).
“OUTPUTS/PYTHON/” directory contains Python extensions for Python (in different sub-directories).
The ruby and python libraries must be used with the appropriate 32 bits distribution of ruby or python. (Note that 32 bits programs and libraries can be used on 32 bits or 64 bits LINUX installations.)
In archive “FeResPost_5.0.9_LINUX_64.7z” the binaries contain ruby wrappers and C++ library:
“OUTPUTS/lib” directory contains the file “libFeResPost_5.0.9.so” that corresponds to the FeResPost C++ library without any wrapper. If you intend to work with the C++ shared library, this file should be located in a library standard directory, or in a library pointed to by environment variable “LD_LIBRARY_PATH”.
“OUTPUTS/include” directory and its subdirectories contain FeResPost C++ headers. You have no use of these files unless you wish to develop your own wrapper for FeResPost (for use with Python, Perl, Java...), or use FeResPost C++ library in one of your C++ applications. So most of you can forget this directory.
“OUTPUTS/RUBY/” directory contains RUBY extensions (in different sub-directories).
“OUTPUTS/PYTHON/” directory contains Python extensions for Python (in different sub-directories).
The ruby and python libraries must be used with the appropriate 64 bits distribution of ruby or python.
In archives “FeResPost_win32_5.0.9_*.7z” and “FeResPost_win32_5.0.9_gcc345_*.7z” the binaries contain ruby wrappers, COM component and C++ library:
“OUTPUTS/lib” directory contains the file “libFeResPost_5.0.9.dll” that corresponds to the FeResPost C++ library without any wrapper. If you intend to work with this shared library, this file should be located in a directory that appears in the “Path” environment variable. (The FeResPost extension shared libraries are linked to this C++ library so that it must be accessible.)
“OUTPUTS/include” directory and its subdirectories contain FeResPost C++ headers. You have no use of these files unless you wish to develop your own wrapper for FeResPost (for use with Python, Perl, Java...), or use FeResPost C++ library in one of your C++ applications. So most of you can forget this directory.
“OUTPUTS/RUBY/” directory contains RUBY extensions for ruby (in different sub-directories).
“OUTPUTS/PYTHON/” directory contains Python extensions for Python (in different sub-directories).
“OUTPUTS/COM” contains the directories and files for the COM component (dll and tlb files). Information on the installation of the COM component on Windows is given in section X.A.4.5.
The ruby and python libraries must be used with the appropriate 32 bits distribution of ruby or python. (Note that 32 bits programs and libraries can be used on 32 bits or 64 bits LINUX installations.) The “*” in archive name can be “w10” or “w11”, depending on the computer on which the libraries have been compiled (Winfows 10 or Windows 11).
“FeResPost_win32_5.0.9_gcc345_*.7z” archive contains libraries that have been compiled with an older version of GNU compiler (GCC 3.4.5). This older version of the library does not allow to compile FeResPost extension for ruby versions more recent than ruby 2.3.*. On the other hand, the C++ standard library to which FeResPost is linked allows a random access to XDB of FAC files of size larger than 2Gb. It seems that more recent versions of GNU compiler no longer allows this, and this is a regression.
We cond have decided not to distribute the 32bits Windows binaries as nowadays, most computers run 64bits operating systems. We think however that, at least for the COM component, the availability of 32bits binaries may be useful to many. Indeed, many Microsoft Office installations are still 32 bits, and FeResPost 32bits COM component is then necessary.
In archive “FeResPost_win64_5.0.9_*.7z” the binaries contain ruby wrappers, COM component and C++ library:
“OUTPUTS/lib” directory contains the file “libFeResPost_5.0.9.dll” that corresponds to the FeResPost C++ library without any wrapper. If you intend to work with this shared library, this file should be located in a directory that appears in the “Path” environment variable. (The FeResPost extension shared libraries are linked to this C++ library so that it must be accessible.)
“OUTPUTS/include” directory and its subdirectories contain FeResPost C++ headers. You have no use of these files unless you wish to develop your own wrapper for FeResPost (for use with Python, Perl, Java...), or use FeResPost C++ library in one of your C++ applications. So most of you can forget this directory.
“OUTPUTS/RUBY/” directory contains RUBY extensions for ruby (in different sub-directories).
“OUTPUTS/PYTHON/” directory contains Python extensions for Python (in different sub-directories).
“OUTPUTS/COM” contains the directories and files for the COM component (dll and tlb files). Information on the installation of the COM component on Windows is given in section X.A.4.5.
The ruby and python libraries must be used with the appropriate 64 bits distribution of ruby or python. There is no issue related to random access to large XDB or FAC files with 64bits versions of FeResPost binaries. The “*” in archive name can be “w10” or “w11”, depending on the computer on which the libraries have been compiled (Winfows 10 or Windows 11).
In archive “FeResPost_NET_5.0.9.7z” the assemblies are distributed in directory “OUTPUTS/NET”. Three versions of FeResPost .NET assembly are build:
In directory “OUTPUTS/NET/X86_CLR2”, one distributes 32 bits managed assembly that targets CLR version 2.0. It should work with programs compiled under .NET Frameworks versions 2.0, 3.0 and 3.5.
In directory “OUTPUTS/NET/X86_CLR4”, one distributes 32 bits managed assembly that targets CLR version 4. It should work with programs compiled under .NET Frameworks versions 4, 4.5 (4.5.1 and 4.5.2) and 4.6 (4.6.1).
In directory “OUTPUTS/NET/X64_CLR4”, one distributes 64 bits managed assembly that targets CLR version 4. It should work with programs compiled under .NET Frameworks versions 4, 4.5 (4.5.1 and 4.5.2) and 4.6 (4.6.1).
As explained in section III.1.1.11, to access HDF files, the first step is to load the HDF5 shared library. The libraries that have been used for the compilation of FeResPost are re-distributed in directory “HDF5_REDISTR”. (See the “Downloads” page on FeResPost web site.)
All the sources are delivered in an archive containing an SRC directory and several levels of sub-directories. The sources of the program are delivered with different Makefiles and BASH or BAT scripts that can be used for the compilation of the different targets:
The makefiles must be used with the GNU “make” command. This means that on Windows OS, you should install the corresponding binaries. We use “MSYS” for several UNIX commands, and have tested different versions of the GNU C/C++ compilers downloaded with different versions of “MINGW”. The compilation has also been tested with different versions of Microsoft Visual C++ compiler.
The “BASH” and “BAT” scripts are located in the “SRC” main directory. “BAT” scripts are used for the compilation on Windows OS, and “BASH” scripts on LINUX. These scripts define part of the compilation environment, and you may have to modify them if you want to recompile the sources.
The main Makefiles are located in “SRC/MAKEFILES” directory. They include sub-makefiles located in the “SRC/MAKEFILES” directory and in the sources sub-directories. The Makefiles in “SRC/MAKEFILES” directory also define part of the compilation environment and will have to be adapted in order to re-compile the sources. These adaptations consist mainly in modifying paths to match installation on your computer. (Ruby installation directory, for example.)
The makefiles in source directories are built automatically. You just have to ask for the building of “dependences” target. For example,you type the command “build_mingw32.bat dependences”. (You do not need to do this if you do not modify the sources.)
The association of script commands, makefiles and targets is summarized in Table X.A.1. Besides, one also defines several targets that do not depend on the platform:
“clean” cleans all the objects, libraries and other files produced by the compiler command.
“dependences” produces or updates the makefiles in the source directories.
“ruby” to build all the ruby extensions available in the Makefile.
“python” to build all the python extensions available in the Makefile.
“com” to build the COM component.
“archives” creates a 7Zip archive of the “OUTPUTS” directory.
“outputs” produces all the libraries in other outputs in “OUTPUTS” directory, and then builds the “archive”
Some targets are specific to the .NET assembly compilation:
“signkey” for the update of the assembly signature.
“install” to install the assembly in the Global Assembly Cache (GAC).
On Windows OS, the compilation of python extension is possible with the MSVC compilers (“build_python_msvc32.bat” and “build_python_msvc64.bat” scripts) or with GNU compiler (“build_mingw32.bat” and “build_mingw64.bat” scripts). We advise to use the GNU compilers as it allows to build all the 32-bits python extensions with a single version of the compiler.
Examples of builds follow:
build_linux32.bash ruby build_linux32.bash ruby_23 build_linux32.bash outputs build_mingw64.bat com build_mingw64.bat ruby build_mingw64.bat vbaruby build_mingw64.bat outputs build_python_27.bat buildbuild_python_win32 buildbuild_python_win64 ...
Note: for 32bits version 2.4.* of ruby, the “include/ruby/ruby.h” has been slightly modified: “DEPRECATE_BY” lines 1381 and 1390 have been commented. Otherwise, the compilation resulted in error messages. This has been done on Windows and on Linux.
| SCRIPT | main Makefile | targets |
| build_linux32.bash | Makefile.LINUX_586 | ruby_31, ruby_30, ruby_27, ruby_26, ruby_25, ruby_24, ruby_23, ruby_22, ruby_21, ruby_20, ruby_19, ruby_18, python_26, python_27, python_30, python_31, python_32, python_33, python_34, python_35, python_36, python_37, python_38, python_39, python_310, develop |
| build_linux64.bash | Makefile.LINUX_I64 | ruby_32, ruby_31, ruby_30, ruby_27, ruby_26, ruby_25, ruby_24, ruby_23, ruby_22, ruby_21, ruby_20, ruby_19, ruby_18, python_26, python_27, python_30, python_31, python_32, python_33, python_34, python_36, python_37, python_38, python_39, python_310, python_311, develop |
| build_mingw32.bat | Makefile.WIN.32 | com, ruby_27, ruby_26, ruby_25, ruby_24, ruby_22, ruby_21, ruby_20, ruby_19, ruby_18, vbaruby, develop, python_26, python_27, python_30, python_31, python_32, python_33, python_34, python_35, python_36, python_37, python_38, python_39 |
| build_mingw32_345.bat | Makefile.WIN.32
(345 targets) HDF5 unsupported | com, ruby_23, ruby_22, ruby_21, ruby_20, ruby_19, ruby_18, vbaruby, develop, python_26, python_27, python_30, python_31, python_32, python_33, python_34, python_35, python_36, python_37, python_38, python_39 |
| build_mingw64.bat | Makefile.WIN.64 | com, ruby_32, ruby_31, ruby_30, ruby_27, ruby_26, ruby_25, ruby_24, ruby_23, ruby_22, ruby_21, ruby_20, develop, python_30, python_31, python_32, python_33, python_34, python_35, python_36, python_37, python_38, python_39, python_310, python_311 |
| build_net.bat | Makefile.NET | net |
| build_msvc_x86.bat | Makefile.MSVC_X86 | com, ruby, python, vbaruby, develop (for debugging the sources) |
| build_msvc_x64.bat | Makefile.MSVC_X64 | com, ruby, python, vbaruby, develop (for debugging the sources) |
| build_intel.bat | Makefile.INTEL.X64 | com, python, vbaruby, develop (for debugging the sources) |
In general, the binaries are compiled without the “-static” option. This means that when using the different shared libraries, the redistributable libraries in "OUTPUTS/REDISTR" directory must be in the PATH environment variable. Compilation is done this way because the “-static” option tends to break the C++ management of exception and associated error messages.
There is one exception: the Python Windows libraries are compiled with “-static” option. This seems not to lead to issues with the management of exceptions.
Of course, users that compile libraries from he sources are free to experiment other options.
One makes below the distinction between the installation of the ruby extension, the COM server and the .NET assembly. Actually, depending on what you want to do, only some parts of the binaries must be installed/configured. Table X.A.2 summarizes what you need to do. Before configuring FeResPost, always make sure that you are selecting the right version of the binaries. In particular:
For ruby and python extensions:
Make sure that you are using the FeResPost extension library that matches your ruby version.
Chose the right version among LINUX and Windows binaries.
Chose the appropriate version among 32 bits and 64 bits libraries (for ruby wrapper library as well as FeResPost C++ library).
For COM component (on Windows), chose the Windows 32 or 64 bits C++ libraries for Windows.
There is no significant risk of mistake for the .NET assembly, but you have to chose between CLR2 and CLR4, and between 32 bits and 64 bits versions (for CLR4). Actually, CLR2 is rather old, so that CLR4 should work on most computers.
If you want to... | You must... |
Use FeResPost in ruby scripts | Install the corresponding FeResPost C++ ruby extension (section X.A.4.3) |
Use FeResPost as COM component (Windows only) | Install and register the COM component (section X.A.4.5) |
Use the .NET assembly | Install the assembly in GAC (global assembly cache) as explained in section X.A.4.6. An installation of the redistributable Microsoft Visual C++ libraries may also be necessary. |
Develop you own wrapper around FeResPost C++ library, or write a program that directly uses the C++ library | Install the C++ library and corresponding header files (section X.A.4.2) |
Modify and/or recompile the sources | Copy the sources and try to find inspiration in the information provided in section X.A.2 |
In principle redistributable libraries are no longer needed as the Windows ruby and python extensions, and the COM component are now statically linked to GNU compiler libraries (“limb.a‘”, “libstdc++.a”,...). However, you might need the redistributable libraries if you used the C++ shared libraries to compile your own executables with FeResPost.
GNU C++ compiler the C++ developer’s library, the ruby extensions or the COM component. (See below.) With recent versions of the compiler, some of the C++ built-in libraries are not included in FeResPost “dll” or “so” library file. Then these libraries are provided in “REDISTR” directory. Then, the user must give access to these libraries to each script or application that uses FeResPost library. For example:
The simplest way to access the redistributable libraries is to add the complete directory name to your PATH environment variable.
You can also copy the redistributable dll files in a directory already point to by your PATH environment variable.
Possibly, the libraries are already installed on your computer and properly referenced by your PATH variable. It might be the case if you have an installation of the appropriate version of GNU compiler, or of a program that has been compiled with this compiler.
On Windows OS, your PATH environment variable can be modified in “Control Panel” –> “System and Security” –> “System” –> “Advanced system settings” –> “Environment variables”.
On your computer, you may run FeResPost from different environments (excel with VBA, ruby, python...) that can require sometimes a 32 bits version, or a 64 bits version of the library and associated redistributables. Or you may compare results obtained with different versions of FeResPost. Then, it may be handy to define the environment associated to each separate script. This can be done by providing the execution environment in a script (BAT file on windows, and bash or csh file on UNIX for example).
For example, on Windows, assuming you are using a 64 bits version of excel, and that the 64 bits version of the COM component has been properly registered, excel could be run by the following batch file:
setlocal set PATH=D:/SHARED/FERESPOST/SRC/OUTPUTS/REDISTR;C:/NewProgs/RUBY/Ruby200_x64/bin; C:\Program Files (x86)\Microsoft Office\Office12 excel LaminateAnalysis.xlsm endlocal
(This is just an example, you have to adapt the PATH variable to your installation.)
One distinguishes the UNIX/LINUX OS and Windows OS:
On UNIX/LINUS OS, the file “libFeResPost_5.0.9.so” should be located in a library standard directory, or in a library pointed to by environment variable “LD_LIBRARY_PATH”. (If necessary, this variable can be modified to contain the path to directory in which you copy the library.)
On Windows OS, the library “libFeResPost_5.0.9.dll” should be located in a directory that appears in the “Path” environment variable. (If necessary, this variable can be modified to include the path to the directory in which you copy the library.)
(Note that the use of these shared libraries is no longer recommended. Instead, it is a better idea to statically link your libraries/executables to FeResPost objects.)
for the headers, just copy the “include” directory in a location that suits you, and adapt your compiler options to access the headers (for example, by editing your makefiles).
The shared library (FeResPost.so or FeResPost.dll) is delivered with “FeResPost.rb” ruby file. This file is the ‘main” file that loads the shared library and defines the elements that allow to “coerce” the arguments of “Result” class operators. (See section I.7.)
The files should be copied into the ruby installation library directory. The files can also be installed in another directory, but then the access path must be specified to ruby. (For example, with “-I” option.) You can also install them in any directory that suits you and ensure that “RUBYLIB” environment variable points to that directory.
The shared library (FeResPost.so or FeResPost.pyd) contain everything you need to run the examples. The files should be copied into the Python installation library directory. You can also copy Python library in you user site packages directory. This can be obtained via the command:
python -l --user-site
The files can also be installed in another directory, but then the access path must be specified to Python.
You can also install them in any directory that suits you and ensure that “PYTHONPATH” environment variable points to that directory.
Note that the Python examples are provided with with “env*’ batch files that help you to define the approrpiate environment on Windows.
Two solutions are proposed for the registration or un-registraition of COM component. One can use “modifyRegistry.exe” program”. Registration or un-registration is also possible using “reg” files.
COM server must be registered before use. For that purpose, a program called “modifyRegistry.exe” is distributed with FeResPost library. This program is used to add keys to the Windows register. Follows some information:
The component can be registered for the current user only, or for all the users. In the second case, the registration program should be used on an account that has administrator privileges.
The registration program allows to register the component as well as to unregister it.
The registration program allows the user to select the part that shall be installed among:
The in-proc library “FeResPost.dll”,
The type library “FeResPost.tlb”,
The registration of type library (TLB) is not necessary if the COM component is used from compiled language. But the user must register the type library to use the component from interpreted languages VBA, ruby, python...
The standard and recommended configuration involves the registration of the in-proc library “FeResPost.dll’, and of the type library “FeResPost.tlb”.
Among the keys and values that are written to the Windows registry, the full paths to the dll, exe and tlb appear several times. This means that ones the component has been registered, these files should not be moved. So, a proper location for the FeResPost library should be selected prior to its registration.
Several versions of FeResPost COM component can be installed at the same time on the same computer.
The examples presented in Part VII require only the registration of in-proc library and type library (recommended configuration).
Figure X.A.1 shows the window created by the "modifyRegistry.exe" program. After clicking one of the registration buttons, the program shows an information message allowing to check the correct installation of COM component (Figure X.A.2 or X.A.3). In many cases, failure is related to the impossibility of loading FeResPost library.
You may register either 32 bits version of the component, or 64 bits version of the component, or both 32 bits and 64 bits versions of the component:
The 64 bits version of the component works on 64 bits Windows only. On the other hand, the 32 bits version works on 32 bits as well as 64 bits versions of Windows. This means that the registration of both 32 and 64 bits versions of the COM component is possible only on 64 bits Windows OS.
Windows manages the writing of kes in the appropriate directories of the register. For example, when 32 bits component is registered in 64 bits Windows OS, CLASSES keys are defined in “HKLM/Software/Wow6432Node/Classes/CLSID” directory.
The registration is done with “modifyRegistry.exe” executable. The 64 bits “modifyRegistry.exe” must be used to register the 64 bits library, and the 32 bits “modifyRegistry.exe” must be used to register the 32 bits library.
The “dll” library name is the same for 32 bits and 64 bits versio of the component. Therefore, the two dll files must be located in separate and preferably clearly identified directories.
The “tlb” file must be registered only once. For example, a possible scenario is to register the 32 bits “dll” library and the “tlb” file 32 bits version of “modifyRegistry.exe”, then use the 64 bits version of “modifyRegistry.exe” to register 64 bits “dll” library.
It is not always easy to determine whether the 32 bits or the 64 bits version of COM component is to be used. For example, 64 bits versions of ruby or python seem to require the 32 bits components that are accessed through “win32ole” or “win32con” extesnions. Therefore, it may be a good idea to register the two versions.
When one gets rid of an older version of FeResPost, the 32 bits and 64 bits versions of the components must be un-registered separately.
FeResPost COM component is delivered with registration files in the “OUTPUTS/COM/REGFILES” directory. Four such files are available: “addAllUsers.reg”, “addCurrentUser.reg”, “removeAllUsers.reg” and “removeCurrentUser.reg”. The four files can be distinguished according to two criteria:
Two of the files add information to Windows registry, and two of the files are used to clean information from Windows registry.
Two of the files can be used to modify information for all users, and two of the files for current user only. To modify Windows registry information for all users requires Administrator privileges.
Before using the reg files that add information to Windows registry, you must ensure that the paths to “FeResPost.dll” and “FeResPost.tlb” match what their actual location on your computer. For example, the registry files delivered with COM binaries contain this kind of information:
[HKEY_CURRENT_USER\Software\Classes\TypeLib\{0A88E969-53D5-492B-FABB-A0DF12862BE8}\1.0\0\win32]
@="C:\\Users\\ferespost\\Documents\\SRC\\OUTPUTS\\COM\\lib\\FeResPost.tlb"
...
[HKEY_CURRENT_USER\Software\Classes\CLSID\{52FEFC92-63E7-4500-768B-84B08E1262C1}\InprocServer32]
@="C:\\Users\\ferespost\\Documents\\SRC\\OUTPUTS\\COM\\lib\\FeResPost.dll"
"ThreadingModel"="apartment"
(Of course, the paths must be modified to match your installation.)
The sources come with a ruby script that is used to generate the registration files. The script can be used as follows:
ruby bin/createRegFiles.rb C:/Users/ferespost/Documents/SRC C:/Users/ferespost/Documents/SRC/OUTPUTS/COM 5.0.7 32
The three arguments of the ruby script are:
A string corresponding to the path to sources directory. The script needs this path because it reads the “idl” source files to identify the different GUIDS and associate them to classes and interfaces.
A string containing COM directory. The “REGFILES” directory containing all the registration files is located in that COM directory. (It is created if necessary.)
The third argument is a string identifying the version of COM component. We usally choose FeResPost version number. (5.0.7 in this case.) User can choose another identifier.
Last argument is 32 or 64 and specifies whether component is 32 bits or 64 bits.
FeResPost assembly should be installed in the global assembly cache. This can be done by copying the “FeResPost.dll” dynamic link library found in “NET’ directory to the Global Assembly Cache. On my computer, this can be done simply by a drag and drop of “FeResPost.dll” into “C:/Windows/assembly” directory. Note however that:
You may need Administrator’ privileges to perform the operation.
You have to choose the right version of the .NET assembly. (See above.)
You can also use an assembly without registration. Then, the assembly must be located in the same directory as the one containing the executable.
The advantage of installing FeResPost in the Global Assembly Cache is that this allows to use from a program anywhere without minding where to find it.
The modification of coordinate system into which the components of vectorial or tensorial results are expressed is a common operation performed when post-processing finite element results. To perform the transformation some vectorial and tensorial calculation is necessary. One gives in this Appendix, a summary of theoretical background necessary to understand the operations performed with FeResPost.
When performing tensorial calculations, or post-processing results, one manipulates 1D or 2D arrays of real values corresponding to the components of vectors or tensors in a specified coordinate system. Higher order tensors also exist, but they are not manipulated in FeResPost and we do not present the theory for tensor order larger than 2.
A vectorial force can be expressed by its components in the Cartesian coordinate system characterized by its origin and its three unit length mutually orthogonal vectors , and . Then the vector corresponds to:
|
|
In the rest of the text the components of a vector are denoted and one uses the Bose-Einstein convention of summation on repeated indices so that the previous expression is simply written:
|
|
A Cauchy stress tensor is characterized by its components in the Cartesian coordinate system . (One uses the same notations as in section X.B.1.1).
|
|
The nine quantities can be considered as the basic tensors from which all the other tensors are obtained linear combinations. Note that the Cauchy stress tensor is always symmetrical so that .
In sections X.B.1.1 and X.B.1.2, one presented vector and tensor components in Cartesian coordinate systems. The same definition is also worthy in curvilinear coordinate systems. However, the director vectors depend on the point on which the vector or tensor is attached. Conventionally, one decides that the director vectors are chosen tangent to the coordinate lines and are of unit length.
For example, for a cylindrical coordinate system, the position of a point depends on three coordinates , and . So one has:
|
|
Then three tangent vectors are obtained by deriving the position wrt coordinates:
Finally, the three tangent vectors are normalized as follows:
|
|
This process to define base vectors at any point can be generalized to all curvilinear coordinate systems. However, the cylindrical and spherical coordinate systems have a peculiarity: at a given point, the three base vectors are mutually orthogonal. This is not a general characteristic of curvilinear coordinate systems.
The orthogonality property of the coordinate systems one uses in FeResPost simplifies the transformation of components from one coordinate system to another. Indeed such transformations reduce to transformations between Cartesian coordinate systems. There is only one difficulty in this process: to calculate the base vectors at every point.
One considers only the peculiar case of two Cartesian coordinate systems with the same origin. In section X.B.1.3, one showed that even for cylindrical and spherical coordinate systems it is possible to reduce the complexity of the problem to a transformation of the components between two Cartesian coordinate systems.
One considers a vectors with components expressed in two Cartesian coordinate systems with base vectors and respectively. So one has:
|
|
In the last expression we introduce the notations and for the components of vector in and respectively.
It is possible to decompose the vectors as a linear combination of vectors :
|
|
The coefficients are easily calculated. Indeed, the scalar multiplication of the previous equality by gives successively:
or finally:
|
|
By a similar calculation, it is possible to identify the relations between the components of vector expressed in the two coordinate systems:
Finally, one sees that the relation between base vectors and vector components are the same:
|
|
|
|
That’s the reason why the transformation is called a covariant transformation. One also says that or are covariant components of vector in coordinate systems and respectively. In the last vector component transformation one recognizes a classical algebraic result:
|
|
The matrix is orthogonal: and the reverse relation for vector components is:
|
|
Similarly to what has been done for vectors in section X.B.2.1, one derives transformations of the components of tensors. One considers the components of tensor in two coordinate systems:
|
|
Using the same definition of transformation matrix as in section X.B.2.1, one writes:
|
|
|
|
Then, the substitution of the two expressions in the equations defining components gives:
The last expression allows us to extract a relation involving only the components of tensors, and not the base vectors:
|
|
Here again, one recognizes a classical matricial expression:
|
|
A transformation of coordinate systems commonly done is a rotation of the coordinate system around a specified axis passing through the origin of the coordinate system. The resulting coordinate system has the same origin, but its base vectors are modified. A classical use of this operation corresponds to the transformation of vector or tensor results in material, ply or element axes of 2D elements.
For example, let be a unit vector defining the rotation axis and the rotation angle. Then the three transformed base vectors are given by:
|
| (X.B.1) |
In particular, if corresponds to , the three
One gives here additional information on the modification of coordinate systems with Result method “modifyRefCoordSys”. When developing the various transformations possible with this function, one tried to keep as much as possible, the correspondence with Patran (Patran 90) transformations. Sometimes, this process has been partially done by trials and guesses until an agreement was found.
In the rest of the section, one gives the information allowing the user to determine exactly the operations that are performed on finite element entities and coordinate systems to defined the transformed coordinate system. One makes the distinction between local, global and projected coordinate systems.
Several types of local coordinate systems may be defined, and the operations performed to define the coordinate system depend on the case:
The “elemIJK” coordinate system definitions may be found in Patran User Manual. It is also common to the element coordinate systems of most finite element programs. Usually, it is defined with the three first definition nodes of the element. Direction X corresponds to the vector from node 1 to node 3. Direction Y is determined from the position of node 3.
The “plyCS” coordinate system is obtained on surfacic elements with “PCOMP” or “PCOMPG” properties by rotating the local material coordinate system with the appropriate angle around its axis Z. For other elements, the ”plyCS” coordinate system is identical to the material coordinate system.
The “matCS” coordinate system definition depends on the type of element:
For 0D elements, no material coordinate system exists.
For 1D elements, the material coordinate system corresponds the element coordinate systems (i.e. Nastran element coordinate system).
For 2D elements, the material coordinate system can be defined by two methods:
If the material coordinate system is defined by an integer, this integer corresponds to the index of the coordinate system defined in the DataBase. Then the new coordinate system as follows:
The First vector of the coordinate system is extracted.
It is projected on the XY plane defined by the Nastran element coordinate system. This gives the vector X of the local material Cartesian coordinate system.
The Vector Z of the local material Cartesian coordinate system is identical to the vector Z of Nastran element coordinate system.
if the material coordinate system is defined by a real argument, the value corresponds to a rotation angle . Then the local material Cartesian coordinate system is defined as follows:
One first builds the IJK Cartesian coordinate system.
Then the vector X of IJK coordinate system is rotated by an angle around axis of IJK coordinate system.
This rotated vector s projected on the XY plane defined by the Nastran element coordinate system. This gives the vector X of the local material Cartesian coordinate system.
The Vector Z of the local material Cartesian coordinate system is identical to the vector Z of Nastran element coordinate system.
For 3D elements, the material coordinate is generally identified by an integer in the “PSOLID” card. It is then retrieved from the DataBase. If no material coordinate system is specified in the “PSOLID” card, then the material coordinate system corresponds to the Nastran element coordinate system.
The “nodeCS” coordinate system corresponds to the node analysis coordinate system. See Nastran reference guide for more information.
The “elemCS” coordinate system corresponds to the Nastran local coordinate system. See Nastran reference guide for more information. Note that the construction of Nastran local coordinate system for CQUAD and 3D elements is complicated. (See sections X.B.4.4 and X.B.4.5 for more information.)
Global coordinate systems correspond to CoordSys objects. However one makes the distinction between:
The basic coordinate system identified with integer 0.
Coordinate systems which have a correspondence in the DataBase from which they have been or may be extracted. Those coordinate systems are identified with an integer larger than 0.
Other user defined coordinate systems which have no correspondence in the DataBase. They are identified with integer -2000.
Not that the user is responsible for the use he makes on coordinate systems defined in DataBase. In particular, it is true when several DataBases are used.
The projected coordinate system is a local Cartesian coordinate system the definition of which depends on the type of element:
For 0D elements, no coordinate system is build.
For 1D and 3D elements, the Nastran element coordinate system is returned.
For 2D elements, the projection makes sense. The coordinate system is build as follows:
The Z vector is the normal to the surface of the 2D element. For a CTRIA3, the vector Z is constant on the element. But for a CQUAD4 the nodes of which are not co-planar, the vector Z depends on the location on the element.
The direction vector is projected on a plane perpendicular to Z and defines direction X. Note that the direction vector is associated to a coordinate system which may be curvilinear.
Note that for 2D elements, the definition of projected coordinate system is more general that in Patran. Indeed, in Patran, only the vector X of the specified coordinate system is projected.
For CQUAD4 Nastran elements, the origin of the element coordinate system is defined to be the intersection of straight lines AC and BD( A, B, C, and D being the corners of the element). As long as the four defining nodes are co-planar, this definition is sufficient. But otherwise, the two straight lines do not intersection, and a generalization of the definition of the origin has to be found. We decide that the origin of the coordinate system shall be the point closest to the two straight lines AC and BD.
The two straight lines can be defined with corresponding parameterized equations:
|
|
|
|
So, one has to find the parameters and that minimize . The vector can be developed as follows:
where
The square of the norm defined above depends on parameters and and is given by:
|
|
This function must be stationary at the optimum point. Therefore its first derivatives wrt and must be zero:
|
|
This leads to a system of two linear equations with the two unknowns and :
|
|
|
|
These two equations may be rewritten as follows:
|
|
|
|
Or simply
|
|
|
|
This equation simply means that the vector connecting the two optimum points is perpendicular to both lines AC and BD. Finally, after resolution of the system of equations and various substitutions, on finds the origin of coordinate system at:
In Nastran, for 3D elements, the definition of the local element coordinate system is a little tricky, and it is not easy to interpret the information found in the reference manuals. One provides here the interpretation that has been used to build the coordinate systems of 3D elements in FeResPost.
The first step of the local element construction is to build three vectors R, S and T related to the geometry of the element. The way those three vectors are constructed depends on the 3D element that is being constructed. Then the R, S and T vectors are used to build a local Cartesian coordinate system. In Nastran Quick Reference Guide [Sof04b], on gives the following explanation for the CTETRA element:
The element coordinate system is chosen as close as possible to the R, S, and T vectors and points in the same general direction. (Mathematically speaking, the coordinate system is computed in such a way that, if the R, S, and T vectors are described in the element coordinate system, a 3x3 positive definite symmetric matrix would be produced.)
In FeResPost, one makes the assumption that this information is also true for the other 3D elements CHEXA and CPENTA. One gives here the mathematical development that leads us to the definition of local coordinate system.
First, let us introduce the notations: , , . So the element coordinate system is and the three vectors R, S and T are denoted . Then one defines with matrix corresponding to the description of vectors on the base . One has:
|
|
|
|
The above statement is equivalent to state that matrix must be symmetric. So the problem reduces to “find three base vectors such that:
|
|
Note also that this condition makes us think to the polar decomposition theorem that states that a positive definite tensor can be decomposed in the product of an orthogonal tensor and a pure symmetric positive definite tensor. This means that any deformation of a continuum medium can be decomposed in a rigid rotation and a pure deformation. One is actually interested in the rigid rotation that can be expressed by its rotation vector (see section X.B.3). So considering an initial set of base vectors and the three vectors provided as data, one must find the three components of the vector such that the new base vector obtained with equation (X.B.1) satisfy the relation
|
| (X.B.2) |
This set of equations is non linear in the primary unknowns and one solves them by a Newton-Raphson in which successive approximations of the three vectors are calculated. One performs a Taylor expansion of the relation (X.B.2) stopped at the first order:
|
|
|
|
Substituting the two previous expressions in (X.B.2), one obtains successively:
|
|
|
|
|
|
|
| (X.B.3) |
This last expression allows to derive three independent linear equations, with three unknowns . The Newton-Raphson algorithm used looks as follows:
Determine a first estimate of the three vectors . In FeResPost, one chooses parallel to R, perpendicular to plane defined by vectors R and T, and perpendicular to and .
Then one iterates until convergence:
Vector is obtained by solving (X.B.3).
One then obtains the rotation angle and unit rotation vector :
|
|
|
|
New estimates of the base vectors are obtained using (X.B.1).
One assumes convergence if .
Vectorial and tensorial components of Results are sometimes expressed in coordinate systems related to material properties. Of course, this is also the case when laminated properties are attributed to the elements. Then, three different coordinate systems can be used: “plyCS”, “lamCS” and “matCS”.
When vectorial or tensorial Results on composite elements are imported, they are expressed:
In “plyCS” coordinate system if the values are associated to a laminate ply (layerId>0).
In “lamCS” coordinate system for Nastran Results when the values are not associated to a ply (layerId<=0).
In “matCS” coordinate system for Samcef Results when the values are not associated to a ply (layerId<=0).
The difference between Samcef and Nastran is related to the fact that Nastran does not make a difference between material and laminate coordinate systems. Then, one considers that “matCS” == “lamCS”.
When one modifies the reference coordinate system of a Result, the components are actually modified according to the rules presented in Table X.B.1.
| Software | Prop. type | layerId | “matCS” | “lamCS” | “plyCS” |
| Nastran | homogenous | <0 | “matCS” | “matCS” | “matCS” |
| Samcef | homogenous | <0 | “matCS” | “matCS” | “matCS” |
| Nastran | homogenous | >0 | — | — | — |
| Samcef | homogenous | >0 | — | — | — |
| Nastran | laminate | <0 | “lamCS” | “lamCS” | “lamCS” |
| Samcef | laminate | <0 | “matCS” | “lamCS” | “lamCS” |
| Nastran | laminate | >0 | “lamCS” | “lamCS” | “plyCS” |
| Samcef | laminate | >0 | “matCS” | “lamCS” | “plyCS” |
One presents in this Appendix the different Results that are pre-defined in FeResPost. All these Results can be read from Results files produced by different finite element solvers described in Part III. The characteristics of the different Results are described in Tables X.C.1 to X.C.10. The following notations have been adopted:
The entities (Result keys) to which values are attached are noted:
“E” if Result values are attached to element centers,
“N” if Result values are attached to nodes,
“EL” if Result values are attached to element centers and are layered,
“EN” if Result values are attached to element corners,
“ENL” if Result values are attached to element corners and are layered.
Some Results allow several possibilities for the attachment of values.
The tensoriality of Results is noted as follows:
“S” means that the Result has scalar values,
“V” means that the Result has vectorial values,
“T” means that the Result has tensorial values.
The Results have been defined in such a way that each type of Result has only one possible tensoriality.
In the description of Results, one makes the distinction between Real and Complex Results (section X.C.1 and X.C.2 respectively).
A summary of the Results that can be read is given in TableX.C.1 to X.C.10.
| Result | Target | Tensor |
| Name | Entities | Type |
| “Coordinates” | N | V |
| “Displacements, Translational” | N | V |
| “Displacements, Rotational” | N | V |
| “Displacements, Scalar” | N | S |
| “Velocities, Translational” | N | V |
| “Velocities, Rotational” | N | V |
| “Velocities, Scalar” | N | S |
| “Accelerations, Translational” | N | V |
| “Accelerations, Rotational” | N | V |
| “Accelerations, Scalar” | N | S |
| “Applied Loads, Forces” | N | V |
| “Applied Loads, Moments” | N | V |
| “MPC Forces, Forces” | N | V |
| “MPC Forces, Moments” | N | V |
| “MPC Forces, Scalar” | N | S |
| “SPC Forces, Forces” | N | V |
| “SPC Forces, Moments” | N | V |
| “SPC Forces, Scalar” | N | S |
| “Reaction Forces, Forces” | N | V |
| “Reaction Forces, Moments” | N | V |
| “Reaction Forces, Scalar” | N | S |
| “Contact, Contact Pressure” | N | S |
| “Contact, Friction Stress” | N | S |
| “Contact, Nodal Distance” | N | S |
| “Contact, Normal Distance” | N | S |
| “Temperature” | N | S |
| “Temperature Variation Rate” | N | S |
| Result | Target | Tensor |
| Name | Entities | Type |
| “Grid Point Forces, Internal Forces” | EN | V |
| “Grid Point Forces, Internal Moments” | EN | V |
| “Grid Point Forces, MPC Forces” | EN | V |
| “Grid Point Forces, MPC Moments” | EN | V |
| “Grid Point Forces, SPC Forces” | EN | V |
| “Grid Point Forces, SPC Moments” | EN | V |
| “Grid Point Forces, Applied Forces” | EN | V |
| “Grid Point Forces, Applied Moments” | EN | V |
| “Grid Point Forces, Reaction Forces” | EN | V |
| “Grid Point Forces, Reaction Moments” | EN | V |
| “Grid Point Forces, Total Forces” | EN | V |
| “Grid Point Forces, Total Moments” | EN | V |
| Result | Target | Tensor |
| Name | Entities | Type |
| “Mechanical Strain Tensor” (5) | E, EN, EL, ENL | T |
| “Strain Tensor” (5) | E, EN, EL, ENL | T |
| “Stress Tensor” | E, EN, EL, ENL | T |
| “Effective Plastic Strain” (10) | E, EN, EL, ENL | S |
| “Effective Creep Strain” (10) | E, EN, EL, ENL | S |
| “Element Strain Energy” | E | S |
| “Element Strain Energy (Density)” | E | S |
| “Element Strain Energy (Percent of Total)” | E | S |
| “Element Kinetic Energy” | E | S |
| “Element Kinetic Energy (Density)” | E | S |
| “Element Kinetic Energy (Percent of Total)” | E | S |
| “Element Energy Loss” | E | S |
| “Element Energy Loss (Density)” | E | S |
| “Element Energy Loss (Percent of Total)” | E | S |
| Result | Target | Tensor |
| Name | Entities | Type |
| “Beam Axial Strain for Axial Loads” (7) | E, EN | S |
| “Beam Axial Strain for Bending Loads” (7) | E, EN | S |
| “Beam Axial Strain for Total Loads” (7) | E, EN | S |
| “Beam Shear Strain for Torsion Loads” (7) | E, EN | S |
| “Beam Shear Strain for Total Loads” (7) | E, EN | S |
| “Beam Axial Stress for Axial Loads” (7) | E, EN | S |
| “Beam Axial Stress for Bending Loads” (7) | E, EN | S |
| “Beam Axial Stress for Total Loads” (7) | E, EN | S |
| “Beam Shear Stress for Torsion Loads” (7) | E, EN | S |
| “Beam Shear Stress for Total Loads” (7) | E, EN | S |
| “Beam Forces” (1) | E, EN | T |
| “Beam Moments” (1) | E, EN | T |
| “Beam Warping Torque” | E, EN | T |
| “Beam Deformations” (2) | E, EN | T |
| “Beam Velocities” (2) | E, EN | T |
| Result | Target | Tensor |
| Name | Entities | Type |
| “Gap Slips” (8) | E, EN | T |
| “Bush Forces Stress Tensor” (9) | E | T |
| “Bush Forces Strain Tensor” (9) | E | T |
| “Bush Moments Stress Tensor” (9) | E | T |
| “Bush Moments Strain Tensor” (9) | E | T |
| “Bush Plastic Strain” | E, EN | S |
| “Spring Scalar Strain” | E, EN | S |
| “Spring Scalar Stress” | E, EN | S |
| “Spring Scalar Forces” (3) | E, EN | S |
| Result | Target | Tensor |
| Name | Entities | Type |
| “Curvature Tensor” | E, EN | T |
| “Shell Forces” | E, EN | T |
| “Shell Moments” | E, EN | T |
| Result | Target | Tensor |
| Name | Entities | Type |
| “Shear Panel Strain, Max” | E, EN | T |
| “Shear Panel Strain, Average” | E, EN | T |
| “Shear Panel Stress, Max” | E, EN | T |
| “Shear Panel Stress, Average” | E, EN | T |
| Result | Target | Tensor |
| Name | Entities | Type |
| “Composite Failure Index, Tsai-Hill Version 1” | EL, ENL | S |
| “Composite Failure Index, Tsai-Hill Version 2” | EL, ENL | S |
| “Composite Failure Index, Tsai-Hill Version 3” | EL, ENL | S |
| “Composite Failure Index, Tsai-Wu” | EL, ENL | S |
| “Composite Failure Index, Hoffman” | EL, ENL | S |
| “Composite Failure Index, Hashin Version 1” | EL, ENL | S |
| “Composite Failure Index, Hashin Version 2” | EL, ENL | S |
| “Composite Failure Index, Hashin Version 3” | EL, ENL | S |
| “Composite Failure Index, Maximum Strain” | EL, ENL | T (11) |
| “Composite Failure Index, Maximum Strain, CompMax” | EL, ENL | S (11) |
| “Composite Failure Index, Maximum Stress” | EL, ENL | T (11) |
| “Composite Failure Index, Maximum Stress, CompMax” | EL, ENL | S (11) |
| “Composite Failure Index, Stress Ratio” | EL, ENL | S |
| “Composite Failure Index, Strain Ratio” | EL, ENL | S |
| “Composite Failure Index, Rice and Tracey” | EL, ENL | S |
| “Composite Failure Index, Interlaminar Shear Stress” | EL, ENL | S |
| Result | Target | Tensor |
| Name | Entities | Type |
| “Composite Critical Ply Failure Index, Tsai-Hill Version 1” | E, EN | S |
| “Composite Critical Ply Failure Index, Tsai-Hill Version 2” | E, EN | S |
| “Composite Critical Ply Failure Index, Tsai-Hill Version 3” | E, EN | S |
| “Composite Critical Ply Failure Index, Tsai-Wu” | E, EN | S |
| “Composite Critical Ply Failure Index, Hoffman” | E, EN | S |
| “Composite Critical Ply Failure Index, Hashin Version 1” | E, EN | S |
| “Composite Critical Ply Failure Index, Hashin Version 2” | E, EN | S |
| “Composite Critical Ply Failure Index, Hashin Version 3” | E, EN | S |
| “Composite Critical Ply Failure Index, Maximum Strain, CompMax” | E, EN | S (11) |
| “Composite Critical Ply Failure Index, Maximum Stress, CompMax” | E, EN | S (11) |
| “Composite Critical Ply Failure Index, Stress Ratio” | E, EN | S |
| “Composite Critical Ply Failure Index, Strain Ratio” | E, EN | S |
| “Composite Critical Ply Failure Index, Rice and Tracey” | E, EN | S |
| “Composite Critical Ply Failure Index, Interlaminar Shear Stress” | E, EN | S |
| Result | Target | Tensor |
| Name | Entities | Type |
| “Composite Critical Ply, Tsai-Hill Version 1” | E, EN | S |
| “Composite Critical Ply, Tsai-Hill Version 2” | E, EN | S |
| “Composite Critical Ply, Tsai-Hill Version 3” | E, EN | S |
| “Composite Critical Ply, Tsai-Wu” | E, EN | S |
| “Composite Critical Ply, Hoffman” | E, EN | S |
| “Composite Critical Ply, Hashin Version 1” | E, EN | S |
| “Composite Critical Ply, Hashin Version 2” | E, EN | S |
| “Composite Critical Ply, Hashin Version 3” | E, EN | S |
| “Composite Critical Ply, Maximum Strain, CompMax” | E, EN | S (11) |
| “Composite Critical Ply, Maximum Stress, CompMax” | E, EN | S (11) |
| “Composite Critical Ply, Stress Ratio” | E, EN | S |
| “Composite Critical Ply, Strain Ratio” | E, EN | S |
| “Composite Critical Ply, Rice and Tracey” | E, EN | S |
| “Composite Critical Ply, Interlaminar Shear Stress” | E, EN | S |
| Result | Target | Tensor |
| Name | Entities | Type |
| “Temperature Gradient” | E, EN | V |
| “Conductive Heat Flux” | E, EN | V |
| “Specific Heat Energy” | E, EN | S |
| “Applied Heat Flux” | E, EN | S |
In the following remarks about the information given in Tables X.C.1 to X.C.10, one assumes that the international unit system is used.
“Beam Forces” and “Beam Moments” are assumed in FeResPost to be tensorial Results expressed in N or Nm respectively. However several components of the tensor are systematically nil. The non-zero components are:
|
|
There is an approximation for the moments above because the torsional component is calculated wrt cross-section shear centre, and bending components are calculated wrt cross-section centre of inertia.
One assumes that the beam forces are calculated from the Cauchy stress tensor components as follows:
|
|
In which is the surface defined by a cross-section through the beam orthogonal to beam longitudinal axis. (One presumes here that the beam longitudinal direction corresponds to “” axis.) Similarly, one assumes that the bending moments tensor is calculated from the Cauchy stress tensor components as follows:
|
|
In which and are the components of coordinates in section, and correspond to the coordinates of center of gravity of the section, and and correspond to the shear center coordinates. Note also that “Beam Forces” and “Beam Moments” are Results that correspond to most 1D elements. (Bars, beams, rods, bushing elements...). However spring elements do not produce “Beam Forces” and “Beam Moments”.
These conventions ensure that beam forces and moments behave like real order 2 tensors when transformation of coordinates systems are performed. The vectorial forces and moments at the two extremities are easily obtained. Vectors
|
|
correspond to the forces and moments that must be applied on side of the beam. On the side of the beam the components of these vectors must be multiplied by -1.
“Beam Deformations” is a tensorial Result corresponding to the difference of displacements of grids B and A of the beam element. The tensor is expressed in element axes. The “Beam Velocities” Result is the time derivative of the “Beam Deformations”.
Spring forces are scalar. The units depend on the connected components: one has N for displacements and Nm for rotations. (Of course, it is also possible to define springs connecting translational and rotational degrees of freedom, but it is generally an error.)
“Shell Forces” and “Shell Moments” are tensorial Results expressed in N/m or N respectively. These Results contain all the force and moment tensors produced by 2D elements. The non-zero components are:
|
|
(Symbol has been used for the out-of-plane shear force.)
One assumes that the shell in-plane forces are calculated from the Cauchy stress tensor components as follows:
Similarly, one assumes that the bending moments tensor is calculated using the distribution through the thickness of the Cauchy stress tensor components as follows:
This is a usual convention for shell elements. For example, this is generally the convention used to present the theory of classical laminate analysis. When a component of the bending tensor is positive, the corresponding component is positive on the upper surface of the shell, and negative on the other face.
The shear components of strain tensors Results stored in FeResPost are the .
The shell curvature tensor is defined as follows:
|
|
Here again, a positive curvature means that the corresponding component of strain tensor is in tension on the upper face, and in compression on the lower face of the shell.
Beam stresses and strains are always scalar Results corresponding either to the axial component, or to the norm of the shear components. Depending on the type of element, the axial stress may be calculated from the axial or bending loads, or to involve both contributions.
Gap elements produce various results. Results are vectorial or tensorial and:
Gap forces results are stored in “Beam Forces” tensorial Result as indicated in remark 1. The value of the axial component is multiplied by “-1.0”, because it is a compression component.
“Beam Deformations” and “Beam Velocities” are tensorial Results containing the relative displacements or velocities of end nodes B and A in element coordinate system.
“Gap Slips” is identical to “Beam Deformations” except that the axial component is set to “0.0”.
Bushing elements produce Stress and Strain tensors obtained by multiplying the Beam Forces and Beam Moments by specified constants. These constants are by default set to 1. Therefore, stresses and strains have often values identical to the forces and moments. Note that the meaning of modifications of coordinate systems for bush stresses and strains have may be discussed. This is particularly so for stresses and strains corresponding to moments.
Composite Results have non-linear dependence on the primary unknowns (displacements). Therefore, composite Results obtained by linear combination of elementary Results are false. This remark applies to all non-linear Results, plastification Results...
Actually “Maximum Strain” and “Maximum Stress” composite Results are not tensorial because each component is a separate scalar Result. So no modification of coordinate system can be done for these Results.
The corresponding “CompMax” scalar Results are obtained by selecting the maximum failure index value among the six components.
The Complex Result types are summarized in Tables X.C.12 to X.C.16.
| Result | Target | Tensor |
| Name | Entities | Type |
| “Displacements (RI), Translational” | N | V |
| “Displacements (RI), Rotational” | N | V |
| “Displacements (MP), Translational” | N | V |
| “Displacements (MP), Rotational” | N | V |
| “Velocities (RI), Translational” | N | V |
| “Velocities (RI), Rotational” | N | V |
| “Velocities (MP), Translational” | N | V |
| “Velocities (MP), Rotational” | N | V |
| “Accelerations (RI), Translational” | N | V |
| “Accelerations (RI), Rotational” | N | V |
| “Accelerations (MP), Translational” | N | V |
| “Accelerations (MP), Rotational” | N | V |
| “Applied Loads (RI), Forces” | N | V |
| “Applied Loads (RI), Moments” | N | V |
| “Applied Loads (MP), Forces” | N | V |
| “Applied Loads (MP), Moments” | N | V |
| “MPC Forces (RI), Forces” | N | V |
| “MPC Forces (RI), Scalar” | N | S |
| “MPC Forces (MP), Forces” | N | V |
| “MPC Forces (MP), Scalar” | N | S |
| “SPC Forces (RI), Forces” | N | V |
| “SPC Forces (RI), Moments” | N | V |
| “SPC Forces (MP), Forces” | N | V |
| “SPC Forces (MP), Moments” | N | V |
| Result | Target | Tensor |
| Name | Entities | Type |
| “Beam Axial Strain for Axial Loads (RI)” (7) | E, EN | S |
| “Beam Axial Strain for Bending Loads (RI)” (7) | E, EN | S |
| “Beam Axial Strain for Total Loads (RI)” (7) | E, EN | S |
| “Beam Shear Strain for Torsion Loads (RI)” (7) | E, EN | S |
| “Beam Axial Strain for Axial Loads (MP)” (7) | E, EN | S |
| “Beam Axial Strain for Bending Loads (MP)” (7) | E, EN | S |
| “Beam Axial Strain for Total Loads (MP)” (7) | E, EN | S |
| “Beam Shear Strain for Torsion Loads (MP)” (7) | E, EN | S |
| “Beam Axial Stress for Axial Loads (RI)” (7) | E, EN | S |
| “Beam Axial Stress for Bending Loads (RI)” (7) | E, EN | S |
| “Beam Axial Stress for Total Loads (RI)” (7) | E, EN | S |
| “Beam Shear Stress for Torsion Loads (RI)” (7) | E, EN | S |
| “Beam Axial Stress for Axial Loads (MP)” (7) | E, EN | S |
| “Beam Axial Stress for Bending Loads (MP)” (7) | E, EN | S |
| “Beam Axial Stress for Total Loads (MP)” (7) | E, EN | S |
| “Beam Shear Stress for Torsion Loads (MP)” (7) | E, EN | S |
| “Beam Forces (RI)” (1) | E, EN | T |
| “Beam Moments (RI)” (1) | E, EN | T |
| “Beam Warping Torque (RI)” | E, EN | T |
| “Beam Forces (MP)” (1) | E, EN | T |
| “Beam Moments (MP)” (1) | E, EN | T |
| “Beam Warping Torque (MP)” | E, EN | T |
| Result | Target | Tensor |
| Name | Entities | Type |
| “Bush Forces Stress Tensor (RI)” (9) | E | T |
| “Bush Forces Strain Tensor (RI)” (9) | E | T |
| “Bush Moments Stress Tensor (RI)” (9) | E | T |
| “Bush Moments Strain Tensor (RI)” (9) | E | T |
| “Bush Forces Stress Tensor (MP)” (9) | E | T |
| “Bush Forces Strain Tensor (MP)” (9) | E | T |
| “Bush Moments Stress Tensor (MP)” (9) | E | T |
| “Bush Moments Strain Tensor (MP)” (9) | E | T |
| “Spring Scalar Strain (RI)” | E, EN | S |
| “Spring Scalar Stress (RI)” | E, EN | S |
| “Spring Scalar Forces (RI)” (3) | E, EN | S |
| “Spring Scalar Strain (MP)” | E, EN | S |
| “Spring Scalar Stress (MP)” | E, EN | S |
| “Spring Scalar Forces (MP)” (3) | E, EN | S |
| Result | Target | Tensor |
| Name | Entities | Type |
| “Curvature Tensor (RI)” | E, EN | T |
| “Shell Forces (RI)” | E, EN | T |
| “Shell Moments (RI)” | E, EN | T |
| “Curvature Tensor (MP)” | E, EN | T |
| “Shell Forces (MP)” | E, EN | T |
| “Shell Moments (MP)” | E, EN | T |
The predefined criteria source code is located in file “SRC/Result/predfinedCriteria.cpp”. So far, five criteria are defined. They are presented in section X.D.1.
Note that the user can define its own criteria, and some preparatory work has already been done. Some explanation is given in section X.D.2.
Only five predefined criteria are available at the moment. They are presented and discussed in the sub-sections that follow. Additional information on what is done in the criterion can be obtained by reading “SRC/COMMON/result/predfinedCriteria.cpp” source file.
This criterion is used to calculate honeycomb core margin of safety according to the so-called “Airbus” core failure criterion than combines the two components of out-of-plane stress tensor. The margin of safety is calculated according to the following expression:
|
|
in which and are the honeycomb longitudinal and transversal shear components of Cauchy stress tensor and and the corresponding allowables.
The arguments of the criterion are given in Table X.D.1. The method returns an Array of 8 elements according to Table X.D.2:
The four first elements correspond to the Result key on which the minimum margin of safety is calculated.
Then, the two components of the out-of-plane shear stress at critical location is given.
Then, one gives the critical (minimum) margin of safety.
The last element of the Array is a Result object that contains the margins of safety element-per-element, node-per-node...
| Pos. | Name | Type | meaning | can be modified? |
| 1 | dB | DataBase | DataBase (or derived) | NO |
| 2 | fos | Real | factor of safety | NO |
| 3 | allL | Real | shear allowable in L-direction | NO |
| 4 | allW | Real | shear allowable in L-direction | NO |
| 5 | stressRes | Result | Cauchy Stress Tensor | NO |
| Pos. | Name | Type | meaning |
| 1 | ElemId | Integer | Critical Element ID |
| 2 | NodeId | Integer | Critical Node ID |
| 3 | LayerId | Integer | Critical Layer ID |
| 4 | SubLayerId | Integer | Critical Sub-Layer ID |
| 5 | sigLmax | Real | L OOP shear component of stress tensor at critical location |
| 6 | sigWmax | Real | W OOP shear component of stress tensor at critical location |
| 7 | mosMin | Real | Critical margin of safety |
| 8 | mosRes | Result | All the margins of safety that have been calculated |
This criterion is used to calculate honeycomb core margin of safety according to the so-called “Airbus” core failure criterion than combines the two components of out-of-plane stress tensor. The margin of safety is calculated according to the following expression:
|
|
in which and are the honeycomb longitudinal and transversal shear components of Cauchy stress tensor and and the corresponding allowables. Actually, one calculates a strength ratio instead of a margin of safety. The relation between strength ratio, reserve factor and margin of safety is as follows:
|
|
This leads to the following expression for the strength ratio:
|
|
(The display of strength ratios instead of margins of safety allows usually a better identification of critical areas. This is true,for example, when results are saved in GMSH format.)
The arguments of the criterion are given in Table X.D.3. Compared to the “HoneycombAirbusMoS” discussed in section X.D.1.1, two new parameters are defined: “strL” and “strW” String arguments. These arguments, allow to specify the Cauchy Stress Tensor components that should be considered for and respectively. Possible values are “XZ”, “ZX”, “YZ”, “ZY”, “XY” and “YX”. (This capability has been added to allow the post-processing of stress when the usual convention for honeycomb core material definition have not been followed.
The method returns an Array of 8 elements according to Table X.D.4:
The four first elements correspond to the Result key on which the minimum margin of safety is calculated.
Then, the two components of the out-of-plane shear stress at critical location is given.
Then, one gives the critical (maximum) strength ratio.
The last element of the Array is a Result object that contains the strength ratio element-per-element, node-per-node...
| Pos. | Name | Type | meaning | can be modified? |
| 1 | dB | DataBase | DataBase (or derived) | NO |
| 2 | fos | Real | factor of safety | NO |
| 3 | allL | Real | shear allowable in L-direction | NO |
| 4 | allW | Real | shear allowable in L-direction | NO |
| 5 | strL | String | shear allowable in L-direction | NO |
| 6 | strW | String | shear allowable in L-direction | NO |
| 7 | stressRes | Result | Cauchy Stress Tensor | NO |
| Pos. | Name | Type | meaning |
| 1 | ElemId | Integer | Critical Element ID |
| 2 | NodeId | Integer | Critical Node ID |
| 3 | LayerId | Integer | Critical Layer ID |
| 4 | SubLayerId | Integer | Critical Sub-Layer ID |
| 5 | sigLmax | Real | L OOP shear component of stress tensor at critical location |
| 6 | sigWmax | Real | W OOP shear component of stress tensor at critical location |
| 7 | srMax | Real | Critical strength ratio |
| 8 | srRes | Result | All the strength ratios that have been calculated |
This criterion is used to calculate Von Mises margin of safety. The margin of safety is calculated according to the following expression:
|
|
|
|
The arguments of the criterion are given in Table X.D.5. The method returns an Array of 7 elements according to Table X.D.6:
The four first elements correspond to the Result key on which the minimum margin of safety is calculated.
Then, Von Mises equivalent stress at critical location.
Then, one gives the critical (minimum) margin of safety.
The last element of the Array is a Result object that contains the margins of safety element-per-element, node-per-node...
| Pos. | Name | Type | meaning | can be modified? |
| 1 | dB | DataBase | DataBase (or derived) | NO |
| 2 | fos | Real | factor of safety | NO |
| 3 | sigAll | Real | allowable stress | NO |
| 4 | stressRes | Result | Cauchy Stress Tensor | NO |
| Pos. | Name | Type | meaning |
| 1 | ElemId | Integer | Critical Element ID |
| 2 | NodeId | Integer | Critical Node ID |
| 3 | LayerId | Integer | Critical Layer ID |
| 4 | SubLayerId | Integer | Critical Sub-Layer ID |
| 5 | vmMax | Real | Von Mises equivalent stress tensor at critical location |
| 6 | mosMin | Real | Critical margin of safety |
| 7 | mosRes | Result | All the margins of safety that have been calculated |
This criterion is used to calculate Von Mises strength ratios. The relation between strength ratio, reserve factor and margin of safety is as follows:
|
|
This leads to the following expression for the strength ratio:
|
|
in which
|
|
The arguments of the criterion are given in Table X.D.7. The method returns an Array of 7 elements according to Table X.D.8:
The four first elements correspond to the Result key on which the minimum margin of safety is calculated.
Then, Von Mises equivalent stress at critical location.
Then, one gives the critical (minimum) margin of safety.
The last element of the Array is a Result object that contains the margins of safety element-per-element, node-per-node...
| Pos. | Name | Type | meaning | can be modified? |
| 1 | dB | DataBase | DataBase (or derived) | NO |
| 2 | fos | Real | factor of safety | NO |
| 3 | sigAll | Real | allowable stress | NO |
| 4 | stressRes | Result | Cauchy Stress Tensor | NO |
| Pos. | Name | Type | meaning |
| 1 | ElemId | Integer | Critical Element ID |
| 2 | NodeId | Integer | Critical Node ID |
| 3 | LayerId | Integer | Critical Layer ID |
| 4 | SubLayerId | Integer | Critical Sub-Layer ID |
| 5 | vmMax | Real | Von Mises equivalent stress tensor at critical location |
| 6 | srMax | Real | Critical strength ratio |
| 7 | srRes | Result | All the strength ratios that have been calculated |
This criterion is used to calculate with a single call three connection failure criteria: sliding, gapping and insert. The calculation is done by calculating strength ratios. The relation between strength ratio, reserve factor and margin of safety is as follows:
|
|
In this case, three strength ratios are calculated:
For the sliding strength ratio, one calculates:
|
|
in which is the friction coefficient between assembled elements and is an estimate of the minimum possible pretension of the bolt.
The gapping strength ratio is given by:
|
|
in which is a parameter that allows to take into account the prying effect related to the bending moment in the connection and is an estimate of the minimum possible pretension of the bolt.
The insert criterion is calculated as follows:
|
|
In which “PSS” is the axial allowable of the insert and “QSS” is its shear allowable.
In these expressions, various scalar values related to the connection force and moment vectors are calculated:
|
|
|
|
|
|
|
|
The arguments of the criterion are given in Table X.D.9:
First argument is a DataBase.
The second argument is a String that corresponds to extraction method. If this argument is “BSHFRC” or “BMFRC”, the forces and moments are assumed to be associated to elements. Otherwise they are associated to nodes. (This parameter influences the critical entity ID returned for each failure criterion.)
Arguments 3 and 4 are Result objects that correspond to the connection forces and moments. Note that these Result objects can be modifed if the predefined criterion is calcualted. It is the case, for example, if the coordinate system wrt which force and moment components are expressed is changed.
Arguments 5 to 8 define the direction vector that allows to convert vectorial forces and moments to the corresponding scalar derived components.
Arguments 9 to 11 correspond to the safety factors of the different criteria. A negative safety factor means that the corresponding criterion must not be calculated. Then the corresponding output values are initalized to Boolean “FALSE”.
Arguments 12 to 16 are clearly presented in Table X.D.9
The method returns an Array of 15 elements (5 elements for each criterion):
Elements 1 to 5 correspond to the sliding criterion and are:
The maximum strength ratio;
The corresponding entity ID (element or node ID),
The corresponding connection axial force.
The corresponding connection shear force.
A Result object containing all the strength ratios.
If the sliding safety factor is negative, the criterion is not calculated, and 5 “FALSE” Booleans are returned.
Elements 6 to 10 correspond to the gapping criterion and are:
The maximum strength ratio;
The corresponding entity ID (element or node ID),
The corresponding connection axial force.
The corresponding connection bending moment.
A Result object containing all the strength ratios.
If the gapping safety factor is negative, the criterion is not calculated, and 5 “FALSE” Booleans are returned.
Elements 11 to 15 correspond to the insert criterion and are:
The maximum strength ratio;
The corresponding entity ID (element or node ID),
The corresponding connection axial force.
The corresponding connection shear force.
A Result object containing all the strength ratios.
If the gapping safety factor is negative, the criterion is not calculated, and 5 “FALSE” Booleans are returned.
| Pos. | Name | Type | meaning | can be modified? |
| 1 | dB | DataBase | DataBase (or derived) | NO |
| 2 | extractionMethod | String | Forces and Moments extraction method | NO |
| 3 | fRes | Result | Vectorial Forces | YES |
| 4 | mRes | Result | Vectorial Moments | YES |
| 5 | csId | String/Integer | Reference coordinate system | NO |
| 6 | vx | Real | X component of connection axis vector | NO |
| 7 | vy | Real | Y component of connection axis vector | NO |
| 8 | vz | Real | Z component of connection axis vector | NO |
| 9 | FoSs | Real | Sliding criterion safety factor | NO |
| 10 | FoSg | Real | Gapping criterion safety factor | NO |
| 11 | FoSi | Real | Insert criterion safety factor | NO |
| 12 | Pmin | Real | Bolt minimum pretension for sliding or gapping | NO |
| 13 | Cf | Real | Friction coefficient for sliding criterion | NO |
| 14 | Lg | Real | Prying length for gapping criterion | NO |
| 15 | PSS | Real | Insert tensile allowable | NO |
| 16 | QSS | Real | Insert shear allowable | NO |
| Pos. | Name | Type | meaning |
| 1 | ssrMax | Real/Boolean | Maximum Strength Ratio (for sliding) |
| 2 | ENId | Integer/Boolean | Critical Element/Node ID (for sliding) |
| 3 | sfAxialMax | Real/Boolean | Axial force in critical connection (for sliding) |
| 4 | sfShearMax | Real/Boolean | Shear force in critical connection (for sliding) |
| 5 | ssrRes | Result/Boolean | All the strength ratios (for sliding) |
| 6 | gsrMax | Real/Boolean | Maximum Strength Ratio (for gapping) |
| 7 | ENId | Integer/Boolean | Critical Element/Node ID (for gapping) |
| 8 | gfAxialMax | Real/Boolean | Axial force in critical connection (for gapping) |
| 9 | gmBendingMax | Real/Boolean | Bending moment in critical connection (for gapping) |
| 10 | gsrRes | Result/Boolean | All the strength ratios (for gapping) |
| 11 | isrMax | Real/Boolean | Maximum Strength Ratio (for inserts) |
| 12 | ENId | Integer/Boolean | Critical Element/Node ID (for inserts) |
| 13 | ifAxialMax | Real/Boolean | Axial force in critical connection (for inserts) |
| 14 | ifShearMax | Real/Boolean | Shear force in critical connection (for inserts) |
| 15 | isrRes | Result/Boolean | All the strength ratios (for inserts) |
One often finds in the literature semi-empirical failure criteria corresponding to the combination of elementary failure modes with different load components. For example, in [otNCE21], one finds two criteria for the verification of ultimate failure of bolt under combined tensile, shear and bending loads:
|
| (X.D.1) |
|
| (X.D.2) |
The derivation of a reserve factor from expressions (X.D.1) or (X.D.2) is not straightforward. Statring from the definition of reserve factor (value by which loads can be multiplied to reach failure), one verifies that for (X.D.1) it corresponds to the value such that
|
| (X.D.3) |
Similarly, for interaction expression (X.D.2), RF is the solution in of
|
| (X.D.4) |
An analytic expression of the solution of equations (X.D.3) or (X.D.4) as a function of the different parameters is generally not available. Then, one must try other ways to calcula numerically. For the three methods “Interaction_2_SR”, “Interaction_3_SR” and “Interaction_N_SR”, we propose a dichotomic solver. The two first methods are specializations of the general case solved by predefined criterion “Interaction_N_SR”. This corresponds to the resolution in of equation:
|
| (X.D.5) |
The arguments of the “Interaction_N_SR” predefined criterion are parameters in the following order: , , ... and :
The parameters are real scalar Result objects. The keys of the different Result objects must match.
The parameters are real values.
(“Interaction_2_SR”, “Interaction_3_SR” criteria need 4 and 6 arguments respectively.) “Interaction_N_SR” predefined criterion returns an Array of two values:
First element is a real value corresponding to .
Second element is a Result object correspond to the different Strength Ratios calculated for the keys of Result objects.
A modified version of the “Interaction_abg_N_SR” predefined criterion corresponds to the resolution in of the following equation:
|
| (X.D.6) |
The arguments of the “Interaction_abg_N_SR” predefined criterion are parameters in the following order: , , , ... and :
The parameters are real scalar Result objects. The keys of the different Result objects must match.
The parameters are real values.
The parameters are real values.
The use that wishes to define his own criteria can do it by inserting code in “SRC/Result/predfinedCriteria.cpp” source file and re-compiling the library. Three areas are to be modified:
One must first define the itneger ID that is associated to the criterion. This is done by inserting the appropriate “#define” statement at the beginning. For example:
#define UD_criterion_1 20001
#define UD_criterion_2 20002
#define UD_criterion_3 20003
#define UD_criterion_4 20004
// ...
in which one assumes that all the user criteria are prefixed with “UD_” string. (It is advised to prefix the criteria following this kind of convention to reduce the risk of clash with someone else’s criterion.)
Then, at the beginning of the “result::calcPredefinedCriterion” method, the mapping between criteria names and integer IDs must be build (“critNameIds” variable). This is currently done by the following C++ lines:
if (bFirstHere) {
critNameIds.insert(make_pair("HoneycombAirbusMoS",HoneycombAirbusMoS));
critNameIds.insert(make_pair("HoneycombAirbusSR",HoneycombAirbusSR));
critNameIds.insert(make_pair("VonMisesMoS",VonMisesMoS));
critNameIds.insert(make_pair("VonMisesSR",VonMisesSR));
critNameIds.insert(make_pair("SGI_SR",SGI_SR));
critNameIds.insert(make_pair("UD_criterion_1",UD_criterion_1));
critNameIds.insert(make_pair("UD_criterion_2",UD_criterion_2));
critNameIds.insert(make_pair("UD_criterion_3",UD_criterion_3));
critNameIds.insert(make_pair("UD_criterion_4",UD_criterion_4));
// ...
}
(Here again, the User is allowed to change the criteria name and associated integer variable names.)
Finally, the new criterion “case” must be defined in the “switch(critId)” case. The case integer ID corrtrsponds to the integer value defined with “#define” statement. The otugh part fo the job is to write the appropriate C++ source code. We hope that the criteria already defined will be a source of inspiration for the developers.
In this Chapter, one presents an example of modular automated post-processing program using the “FeResPost” ruby library. This Chapter is organized as follows:
In section X.E.1, one presents the general architecture of the post-processing program.
In section X.E.2, two post-processing modules of the program are described in detail.
A few last comments are done in section X.E.4.
Different modules corresponding to the different concepts used in the post-processing.
The “LoadCase” modules corresponds to the concept of load case. In our post-processing program, a load case corresponds to the definition of a set of Results, and their association to a DataBase. The Results can be directly read from an “op2” Nastran Result file, or produced by linear combination of elementary Results.
LoadCase module has only one member data: @@dbList. This Hash contains a list of DataBases used for the post-processing.
Several methods are defined:
“getResDirName” returns a String corresponding to a directory in which result files are stored.
“getModelDirName” returns a String corresponding to a directory in which model files are stored.
“createGroups” performs the definition of Groups in a DataBase. The method has two arguments. The first argument is the DataBase object on which Groups are added. The second argument is a String corresponding to the version of the DataBase.
In the example, the method reads Groups from a Patran session files. Then, other Groups are defined by topological operations. The “version” argument is not used because all the DataBases contain the same Group definition. (Generally, Groups defined in different DataBases are not the same.)
The “createGroups” method is used when a new DataBase is defined.
“getDb” method returns the DataBase corresponding to a specified version. The version is given as a String argument. The method first checks if the requested DataBase already exists, i.e. if it is stored in @@dbList member data. If it already exists, the DataBase is returned. If it does not exists, a new DataBase is created. It is read from a BDF file, and groups are defined by a call to “createGroups” methods. The created DataBase is stored in @@dbList and returned.
Finally, the main method is the iterator “each”. This method has one argument corresponding to the version of the loop on load cases. The method defines two “proc1 ” objects:
“postList” loads Results from an op2 file and loops on the corresponding list of load cases. The list is given in the “lcList” Hash. The Results must be read from a single op2 file. The method “yields” and Array containing the DataBase, the name of the load case, and the name of the subcase for which Results are post-processed. After yielding, the Results corresponding to the load case are destroyed.
Note that the programming of this “proc” has been done in such a way that it can easily be switched to read Samcef result. This is the reason which the list of load cases to be processed is given in a Hash argument.
“postCombili” builds Results by linear combination, yields the corresponding Results to a block, then destroys the Results. The created Results are defined by the name of the loadcase, by an Array containing the factors of the linear combination, by the list of elementary load case names.
When the two “proc” objects have been defined, they can be used by the definition of operations to load, yield and destroy Results. This is done in a case statement. One comments below several examples of uses:
A first set of load cases corresponds to the three load cases at constant temperature. They are defined as follows:
case version
when "thermo_const" then
db=getDb("ORBIT")
dirName=getResDirName()
op2Name="temp_disc.op2"
lcList={}
lcList[1]="TEMP_PZ_COLD"
lcList[2]="TEMP_PZ_HOT"
lcList[3]="TEMP_PANLAT_COLD"
lcList[4]="TEMP_PANLAT_HOT"
postList.call
“thermo_const” is the “version” argument of the iterator. One first retrieves the DataBase corresponding to orbital (thermo-elastic) load cases by calling “getDb” method. Then, one specifies which op2 file is to be read. Finally, the list of load cases to be read and post-processed is build. Finally, the proc is called.
One gives below a second example with load cases defined by linear combinations of elementary load cases. The piece of code looks as follows:
when "qs_launch" then
db=getDb("LAUNCH")
dirName=getResDirName()
op2Name="unit_xyz.op2"
elemNames=["LAUNCH_ONE_MS2_X","LAUNCH_ONE_MS2_Y",\
"LAUNCH_ONE_MS2_Z"]
db.readOp2(getResDirName()+"/"+op2Name,"Results",elemNames)
postCombili.call("GLOB_COMPRESSION",[0.0,0.0,-200.0],elemNames)
postCombili.call("GLOB_TENSION",[0.0,-15.0,180.0],elemNames)
postCombili.call("GLOB_LATERAL_1",[30.0,0.0,-50.0],elemNames)
postCombili.call("GLOB_LATERAL_2",[21.21,21.21,-50.0],elemNames)
postCombili.call("GLOB_LATERAL_3",[0.0,30.0,-50.0],elemNames)
postCombili.call("GLOB_LATERAL_4",[-21.21,21.21,-50.0],elemNames)
postCombili.call("GLOB_LATERAL_5",[-30.0,0.0,-50.0],elemNames)
postCombili.call("GLOB_LATERAL_6",[-21.21,-21.21,-50.0],elemNames)
postCombili.call("GLOB_LATERAL_7",[0.0,-30.0,-50.0],elemNames)
postCombili.call("GLOB_LATERAL_8",[21.21,-21.21,-50.0],elemNames)
elemNames.each do |name|
db.removeResults("CaseId",name)
end
elemNames=nil
GC.start
First, the DataBase is prepared and elementary load cases are read from “unit_xyz.op2”. Then the “postCombili” proc objects is called with the appropriate arguments to generate the linear combination of Results. At the end of the calculations, the elementary results are removed from the DataBase.
A peculiar case of iterator is defined by calling each iterator and yielding the returned parameters given in the block:
when "All" then
LoadCases::each("qs_launch") do |db,lcName,scName|
yield([db,lcName,scName])
end
LoadCases::each("thermo_grad") do |db,lcName,scName|
yield([db,lcName,scName])
end
LoadCases::each("thermo_const") do |db,lcName,scName|
yield([db,lcName,scName])
end
One defines two-post-processing modules. The first module, described in section X.E.2.1 uses the Grid Point Forces and Moments to calculate connection margins of safety. The second module, presented in section X.E.2.3 uses the Cauchy stress tensor to calculate margins of safety.
The module “Post_Connect” defines a post-processing of connections considered individually. It builds the Results corresponding to forces and moments at connections. Then, up to three criteria can be calculated. The criteria correspond respectively to sliding, gapping, and failure of inserts.
The member data defined in class “Post_Connect” are given below:
@@fAxial=nil @@fShear=nil @@mTorsion=nil @@mBending=nil
“fAxial”, “fShear”, “mTorsion” and “mBending” contain scalar Results corresponding to different components of the connection loads. These member data are set by method “calcOneInterface”.
This methods builds the scalar Results corresponding to connection loads. It works in several phases:
A Group on which the Results shall be retrieved from the DataBase is build:
grpA = db.getGroupCopy(@@grpNameA)
grpB = db.getGroupCopy(@@grpNameB)
tmpGrp = grpA * grpB
grpC = db.getElementsAssociatedToNodes(tmpGrp)
grpC += tmpGrp
grpC *= grpA
“grpC” is build in such a way that it contains all the elements and nodes necessary to recover the contributing Grid Point Forces (internal forces and moments). Note that, the Groups defined in the DataBase must be such that “grpA” contains all the contributing element and nodes, and “grpB” contains all the contributing nodes.
Parameters are retrieved:
params = getParameters(nil)
csId = params["csId"]
direction = params["direction"]
norme=0.0
for i in 0..2
norme+=direction[i]*direction[i]
end
norme=Math.sqrt(norme)
for i in 0..2
direction[i]/=norme
end
criteriaList=params["criteriaList"]
Note that the list of failure criteria that shall be calculated for each connection is defined in the parameters that are retrieved.
Then, Results are retrieved from the DataBase and used to build the four load components:
tmpForces=db.getResultCopy(lcName,scName,\
"Grid Point Forces, Internal Forces","ElemNodes",grpC,[])
tmpMoments=db.getResultCopy(lcName,scName,\
"Grid Point Forces, Internal Moments","ElemNodes",grpC,[])
tmpForces.modifyRefCoordSys(db,csId)
tmpMoments.modifyRefCoordSys(db,csId)
tmpForces=tmpForces.deriveByRemapping("CornersToNodes",\
"sum",db)
tmpMoments=tmpMoments.deriveByRemapping("CornersToNodes",\
"sum",db)
@@fAxial=tmpForces*direction
@@fShear=sqrt(sq(tmpForces)-sq(@@fAxial))
@@mTorsion=tmpMoments*direction
@@mBending=sqrt(sq(tmpMoments)-sq(@@mTorsion))
Finally, the different criteria in “criteriaList” Array are calculated by calls to the appropriate methods:
criteriaList.each do |critName|
case critName
when "sliding" then
crit_Sliding(db,lcName,scName)
when "gapping" then
crit_Gapping(db,lcName,scName)
when "insert" then
crit_Insert(db,lcName,scName)
end
end
Criteria methods are described below.
This criterion, defined by “crit_Sliding” method is used to calculate sliding margins of safety with the following expression:
|
|
in which is the friction coefficient between assembled elements and is an estimate of the minimum possible pretension of the bolt.
One gives the lines used for the calculation of margins of safety:
mos=(cf*pMin/fos)/(max(@@fAxial,0.0)*cf+@@fShear)-1.0 mosMin=mos.extractResultMin rklMin=mosMin.extractRkl fAxialMin=@@fAxial.extractResultOnRkl(rklMin) fShearMin=@@fShear.extractResultOnRkl(rklMin)
Other programming lines are devoted to the extraction of parameters and printing of Results. One first checks whether the output file exists. If it exists, one opens it in “append” mode. If it does not exists, it is opened in “write” mode and a title line is printed:
if (File.exist?(outputFile)) then
os=File.open(outputFile,"a")
else
os=File.open(outputFile,"w")
os.printf("%30s%40s%10s%8s%10s%8s%8s%14s%14s%8s\n",\
"LoadCase ID","Interface","Elem ID","FoS",\
"Type","Pmin","Cf","Faxial","Fshear","MoS")
end
In either case, the critical margin and corresponding information is printed in the result file:
interfStr=format("%s/%s",@@grpNameA,@@grpNameB)
os.printf("%30s%40s%10s%8.2f%10s%8.1f%8.3f%14.1f%14.1f",\
lcName,interfStr,mosData[1],fos,connectType,pMin,\
cf,fAxialData[5],fShearData[5])
if (mosData[5]>1000.0) then
os.printf("%8s\n",">1000")
else
os.printf("%8.2f\n",mosData[5])
end
Finally, the output stream is closed.
This criterion, defined by “crit_Gapping” method is used to calculate gapping margins of safety with the following expression:
|
|
in which is a parameter that allows to take into account the prying effect related to the bending moment in the connection and is an estimate of the minimum possible pretension of the bolt.
One only gives the lines used for the calculation of margins of safety:
mos=(pMin/fos)/(max(@fAxial,0.0)+@mBending/radius)-1.0 mosMin=mos.extractResultMin rklMin=mosMin.extractRkl fAxialMin=@fAxial.extractResultOnRkl(rklMin) mBendingMin=@mBending.extractResultOnRkl(rklMin)
Other programming lines are devoted to the extraction of parameters and printing of Results.
This criterion, defined by “crit_Insert” method is used to calculate inserts margins of safety with the following expression:
|
|
In which “PSS” is the axial allowable of the insert and “QSS” is its shear allowable.
One only gives the lines used for the calculation of margins of safety:
tmp = sq(@fAxial/pss)+sq(@fShear/qss) tmpMax = tmp.extractResultMax mosMin = (1.0/fos)/sqrt(tmpMax)-1.0 rklMin = mosMin.extractRkl fAxialMin = @fAxial.extractResultOnRkl(rklMin) fShearMin = @fShear.extractResultOnRkl(rklMin)
Other programming lines are devoted to the extraction of parameters and printing of Results.
The interfaces (lists of pair of Groups) on which connection margins will be calculated are defined in “calcAll” method. This method corresponds to a definition of data. One first defines a list of pair of groups with statement like:
list = [] list << ["pan_MX","bar_MXMY"] list << ["pan_MX","bar_MXMZ"] list << ["pan_MX","bar_MXPY"] list << ["pan_MX","bar_MXPZ"] list << ["pan_MX","corner_MXMYMZ"] ...
Then a loop on these data is done, and method “calcOneInterface” is called for each interface:
list.each do |groupNameA,groupNameB| @@grpNameA=groupNameA @@grpNameB=groupNameB calcOneInterface(db,lcName,scName) end
Parameters “@@grpNameA” and “@@grpNameB” are passed by member data of the module. The other parameters are passed as arguments of the call to “calcOneInterface”.
Some parameters depend on the interfaces. For example, the direction of connections, allowables... The method “getParameters” is used to produce the parameters corresponding to each interface.
This method has one parameter “critName” a String argument corresponding to the criterion that requires the parameters. If the argument is nil, one considers that the method is called by “calcOneInterface” and data corresponding to the different orientation of the connection are returned. If the method is called by a criterion method, the data returned correspond to allowables used in the calculation of margins of safety.
The “Post_Connect” module defines methods corresponding to the calculation operations, and methods than can be considered as definition of data. Of course, many different types of data definitions are possible. For example, the definition of interfaces, and of the calculation parameters could be read from a file.
The calculation methods as well as the data are defined in a single module. However, it could be interesting to split the definition of data into several files. This could be interesting, for example, when several persons work on the same project. At the same time, the copying of the methods corresponding to calculation methods into different data files is a poor way to use the object-oriented capabilities of ruby language.
One shows in section X.E.2.3 a different modular design that allows not to repeat the writing of calculation methods, and at the same time to split the module into separate smaller entities. More precisely, one defines a generic “Post_Cauchy” module that performs calculations based on the components of Cauchy stress tensor. Then two modules calculating honeycomb margins of safety and skin margins of safety are defined as two specialized modules using “Post_Cauchy” capabilities.
The module “Post_Cauchy” performs the post-processing of Results corresponding to the Cauchy stress tensor. Presently, three criteria corresponding to the stress tensor are available: an “Airbus” criterion for the calculation of honeycomb, a “MaxShear” criterion for the calculation of honeycomb, and a “VonMises” criterion for the calculation of metallic parts.
The class has three member data:
“groupName” is a String corresponding to the name of the Group of elements for which the post-processing is done.
“layerNames” is an Array of Strings which contains the list of layers for which the Results are retrieved. This variable is initialized by the first call to “getParameters” method.
“stressTensor” contains a Result object with values corresponding to the Cauchy stress tensor for a particular Group and on selected layers. This member data is filled by method “calcOneGroup” is called
This method has one more argument than the corresponding method in “Post_Connect” module:
def Post_Cauchy::calcOneGroup(db,lcName,scName,paramsMethod)
“paramsMethod” is the method to be called when one wishes to retrieve calculation parameters.
“calcOneGroup” performs the building of “stressTensor” member data by retrieving the corresponding Results. The first operations performed by the method are programmed as follows:
grp = db.getGroupCopy(@@groupName) params = paramsMethod.call(nil) interpolation = params["interpolation"] layers = params["layers"] criteriaList=params["criteriaList"] @@stressTensor=db.getResultCopy(lcName,scName,\ "Stress Tensor",interpolation,grp,layers)
So far, the method is not very different than the corresponding method of “Post_Connect” module. Just note the way the parameters method is called.
The rest of the method is similar too:
criteriaList.each do |critName| case critName when "airbus" then crit_HoneyAirbus(db,lcName,scName,paramsMethod) when "maxShear" then crit_HoneyMaxShear(db,lcName,scName,paramsMethod) when "vonMises" then crit_VonMises(db,lcName,scName,paramsMethod) end end
The different methods that performs the criteria calculations are called if necessary. Note that the method to be called to retrieve parameters is passed as argument to the different criteria methods.
This criterion, defined by “crit_HoneyAirbus” method is used to calculate margins of safety in the honeycomb with the following expression:
|
|
in which and are the honeycomb longitudinal and transversal shear components of Cauchy stress tensor and and the corresponding allowables.
As the programming of the criterion is not more complicated than the programming of “Post_Connect” module criteria, one does not describe the instructions.
This criterion, defined by “crit_HoneyMaxShear” method is used to calculate margins of safety in the honeycomb with the following expression:
|
|
in which is the maximum shear stress and the transverse shear allowable.
This criterion, defined by “crit_VonMises” method is used to calculate margins of safety in the metallic parts with the following expression:
|
|
in which is the Von Mises equivalent stress and the material tensile allowable.
This module includes “Post_Cauchy” module:
module Post_honeycomb include Post_Cauchy ...
This means that the methods of “Post_Cauchy” module are now visible in “Post_honeycomb”. In this example, the module has two specific methods:
“calcAll” defines the list of Groups on which honeycomb margins are calculated. Then, a loop on this list is done and the “calcOneGroup” of “Post_Cauchy”
list = ["pan_MX_Honey_50", "pan_MY_Honey_50", "pan_PX_Honey_50",
"pan_PY_Honey_50", "pan_PZ_Honey_72", "pan_SUP_Honey_50"]
list.each do |groupName|
@@groupName=groupName
Post_Cauchy::calcOneGroup(db,lcName,scName,method(:getParameters))
end
Note that the call to “calcOneGroup” has a fourth parameter: the method that shall be called to retrieve the necessary data.
This method “getParameters” is the second method defined in “Post_honeycomb” module. This method is similar to the corresponding method in “Post_Connect” module.
This module is very similar to ‘Post_honeycomb” module.
The file “testSat.rb” contains the “testSat” method that starts the loop on load cases, and where the different post-processing criteria done for each load case are selected.
The different modules that are used in the “testSat” method are made visible by several require statements:
require "util" require "loadCases" require "data_Post_Connect" require "data_Post_honeycomb" require "data_Post_skins"
Then, in “testSat” method, a loop on the load cases is started by calling the “each” iterator of “LoadCases” module with appropriate parameter:
version="All" LoadCases.each(version) do |db,lcName,scName| PostConnect.calcAll(db,lcName,scName) Post_honeycomb.calcAll(db,lcName,scName) Post_skins.calcAll(db,lcName,scName) GC.start end
The different post-processing criteria are called in the block that follows the iterator. At the end of each load case calculation a call to the garbage collector cleans the memory.
One presented in the Chapter a finite element post-processing program written by defining modules. This post-processing works and it is possible to trick the language in order to prevent the rewriting of codes. (See the “Post_Cauchy” class.)
However, the program written in this example uses poorly the object-oriented capabilities of ruby. One presents in Chapter X.E.4 an example of object-oriented post-processing.
This Chapter is devoted to the presentation of an object-oriented post-processing program. The purpose of the example is to illustrate the flexibility that object-oriented programming introduces in the development of post-processing. Note however, that this example requires a better knowledge of object-orientation, and of the ruby language.
The example is very similar to the example presented in Chapter X.D.2. Most programming lines are identical. When presenting the program one only present the different aspects that are specific to the object-orientation of the program. There is however one significant difference between versions “A” and “B” of the post-processing. Version “B” presents one possible programming of dynamic Results post-processing.
The example program is located under "PROJECTb" directory.
One characteristic of the new post-processing, is that it allows to better separate the definition of calculation operations and of the definition of data. Therefore, two directories have been created under "PROJECTb" directory:
Directory "POST" contains the definition of classes used in the post-processing. It corresponds to the definition of calculation operations.
Directory "Data" contains the definition of modules, classes and objects corresponding to the definition of data.
Directory "PROJECTb" still contains the main ruby file "testSat.rb".
Two post-processing classes are defined: "PostCauchy" and "PostConnect". Each of these classes has been obtained by modifying slightly the corresponding post-processing modules of Chapter X.D.2. Note that for connections, new criteria have been defined.
Both classes inherit the generic post-processing class "GenPost". This class is very short, and its main purpose is to manage a list of all the post-processing objects that shall be created when the data are defined (see below). The programming of the class looks as follows:
class GenPost @@postList = [] public def initialize @@postList << self end def GenPost::each @@postList.each do |current| yield current end end end # class Post
The class also defines an iterator that loops on all the instances of the class that have been stored in class member data "@@postList".
One presents below the class "Post_Cauchy" which has been more deeply modified than
"Post_Connect". The inheritance of "GenPost" is ensured by the use of following statements:
require "genPost" class PostCauchy < GenPost
One decided also that member data are no-longer module or class member data. Instead, the become instance member data:
@groupName @layerNames @stressTensor @currentMoSResult @minMosResults
For this post-processing, two member data have been added to allow the storage of results in the object between the different calls to its methods.
One also adds and initializes a method that defines the member data when an instance of the class is created:
def initialize
super
@groupName = nil
@layerNames = nil
@stressTensor = nil
@currentMoSResult = nil
@minMosResults = {}
end
Note the call to "super" that ensures that the corresponding initialize method of "GenPost" class shall be called too. This ensures that each time an instance of "Post_Cauchy" is created, the "GenPost" class is made aware of it, and a pointer to this object is added to its "@@postList" class member data.
Class "Post_Cauchy" defines a method used to write Gmsh result files:
def writeGmshMinMosResults(db,fileName,skeleton) results=[] @minMosResults.each do |key,val| results << [val,key,"ElemCorners"] end db.writeGmsh(fileName,0,results,\ [[skeleton,"mesh_slat"]],\ [[skeleton,"skel_slat"]]) end
the Results stored in the file correspond to those stored in the new member data "@minMosResults". This member data is a Hash that contains the pairs of String identifiers and Results corresponding to minimum margins of safety. This variable is updated at the end of each criterion calculation to contain maps of the minimum margins of safety:
tmpStr=@groupName+"_"+critName if (@minMosResults.has_key?(tmpStr)) then tmpRes1=@minMosResults[tmpStr] tmpRes2=Post.min(tmpRes1,@currentMoSResult) @minMosResults[tmpStr]=tmpRes2 else @minMosResults[tmpStr]=@currentMoSResult end
This method uses the last calculated margin mapping result, stored in "@currentMoSResult".
The Class “PostComposite” calculates composite failure indices and reserve factors for a specified failure criterion. The calculation is done with CLA classes using a loading using finite element “Shell Forces” and “Shell Moments” Results. Practically, one defines a loading as follows:
ld=ClaLoad.new ld.Id="testLoad" ld.setMembrane([0.0,0.0,0.0],"femFM","femFM","femFM") ld.setFlexural([0.0,0.0,0.0],"femFM","femFM","femFM") ld.setOutOfPlane([0.0,0.0],"femFM","femFM") res=db.getResultCopy(lcName,scName,"Shell Forces", interpolation,grp,layers) res.modifyRefCoordSys(db,"lamCS") ld.setShellForces(res) res=db.getResultCopy(lcName,scName,"Shell Moments", interpolation,grp,layers) res.modifyRefCoordSys(db,"lamCS") ld.setShellMoments(res)
Then, the failure indices and reserve factors are calculated as follows:
criteria=[] criteria << ["composite_RF",criterion,"RF",false,false] criteria << ["composite_FI",criterion,"FI",false,false] outputs=db.calcFiniteElementResponse(@compDb,0.0,ld,[false,true,false], [],[],fos,criteria) rfRes=outputs["composite_RF"] fiRes=outputs["composite_FI"]
Note that the calculation uses a composite database stored in “@compDb” member data. This ClaDb object must have been defined before. The class also records envelopes of failure indices in “@minMosResults” member data.
Note that there is a limitation to the post-processing: the thermo-elastic part of the
laminate loading is not considered in this example. Therefore, the results might be inexact
for thermo-elastic load cases (orbit load cases for example). The class is defined in file
“POST/post_Composite.rb”.
The new object-oriented structure for the post-processing also allows the post-processing of dynamic Results. One Presents below two examples of post-processing for dynamic Results.
A new post-processing class is created to allow the presentation of dynamic Results. Actually, this class only extracts the magnitude and phase for one finite element entity and one component, and saves it into an Array, for later output in a text file. The class is called “PostExtract” and has only one member data: “extracts” in which the extracted Results shall be stored.
The “initialize” method calls the constructor of the parent class and initializes “extracts” to a void Hash:
def initialize
super
@extracts = {}
end
Then the sequence of operations to perform the extractions is described below. It is performed by the “calcOneGroup” method:
def calcOneGroup(db,lcName,scName,refName,grpContent,resName, extractMethod,csId,component) ...
The method has nine arguments:
The usual “db”, “lcName” and “scName” arguments.
“refName”: is used to reference the extracted Results in “extracts” member data.
“grpContent” the description of entities for which Results are extracted. This argument contains a String that must correspond to exactly one extracted value. For example: “Element 10”, “Node 17”.
“resName”: a String containing the name of the Result stored in the DataBase “db” and from which one value shall be extracted.
“extractMethod”: a String corresponding to the extraction method of “getResultCopy” DataBase method.
“csId” the identifier of the coordinate system in which the Result shall be expressed. This argument can be an integer or a String.
“component” The name of the component one shall extract. This is a String with 0, 1 or 2 characters. For example: "", "Y", "ZZ", "ZY"... (The void String is used if no extraction operation is necessary. This is the case when the Result obtained from the DataBase is already scalar.
Then the following sequence of operations:
One builds a Group “grp” that shall be used for the extraction of a Result from the DataBase “db”:
grp=Group.new
grp.Name=refName
grp.setEntities(grpContent)
The Result is extracted:
res=db.getResultCopy(lcName,scName,resName,extractMethod,grp,[])
If the Result is vectorial or tensorial, the transformation of coordinate system is done:
if (res.TensorOrder>0) then
res.modifyRefCoordSys(db,csId)
end
One builds a new Result “compRes” by extraction of a component. Of course, if the Result is already scalar, one just performs an assignation operation:
if (component.size==0) then
compRes=res
elsif (component.size==1) then
compRes=res.deriveVectorToOneScal("Component "+component)
elsif (component.size==2) then
compRes=res.deriveTensorToOneScal("Component "+component)
end
Then, one retrieves an Array “grpHashRes” from “extracts” member data. If the Array is not found in the Hash by key “refName”, this means that this key appears for the first time. then, one initializes a new Array and inserts it in “extracts”.
if @extracts.has_key?(refName) then
grpHashRes=@extracts[refName]
else
grpHashRes=[]
@extracts[refName]=grpHashRes
end
Finally, one inserts extracted values in “grpHashRes”. The four values inserted are the output index, the frequency, the magnitude and the phase:
compRes.set2MP
data=compRes.getData
mag=data[0][5]
phase=data[0][6]
grpHashRes << [compRes.getIntId(1),compRes.getRealId(0),mag,phase]
The class “PostExtract” also defines a method for the final processing of the values stored in “extracts” member data. This method, called “gnuplot” outputs the Results in text files created in “OUT_DYNAM” directory. Also, a “dat” file containing the gnuplot commands to create graphical outputs is created in the same directory. The name of this command file is the argument of “gnuplot” method:
def gnuplot(datName)
gnuplotOs=File::open("OUT\_DYNAM/"+datName,"w")
gnuplotOs.printf("\nset terminal png\n\n")
@extracts.each do |key,tabs|
fileName="OUT\_DYNAM/"+key+".txt"
os=File::open(fileName,"w")
tabs.each do |mode,freq,mag,phase|
os.printf("%4d%15g%15g%15g\n",mode,freq,mag,phase)
end
os.close
gnuplotOs.printf("set output \"%s_m.png\"\n",key)
gnuplotOs.printf("plot \"%s.txt\" using 2:3 with lines\n",key)
gnuplotOs.printf("set output \"%s_p.png\"\n",key)
gnuplotOs.printf("plot \"%s.txt\" using 2:4 with points 1\n\n",key)
end
gnuplotOs.close
end
One also defines a modified version of “PostComposite” class devoted to the corresponding post-processing of dynamic results in Real-Imaginary format. This Class is defined in file “POST/post_DynamComposite.rb” and the Class is named “PostDynamComposite” Its definition is nearly the same as the corresponding static class. Only, for each frequency, an additional loop performs the calculation for Real Results extracted at different rotation angles:
... ld=ClaLoad.new ld.Id="testLoad" ld.setMembrane([0.0,0.0,0.0],"femFM","femFM","femFM") ld.setFlexural([0.0,0.0,0.0],"femFM","femFM","femFM") ld.setOutOfPlane([0.0,0.0],"femFM","femFM") forces=db.getResultCopy(lcName,scName,"Shell Forces (RI)", interpolation,grp,layers) forces.modifyRefCoordSys(db,"lamCS") moments=db.getResultCopy(lcName,scName,"Shell Moments (RI)", interpolation,grp,layers) moments.modifyRefCoordSys(db,"lamCS") critTheta=critElem=critNode=critLayer=critSubLayer=critFI=critRF=nil; (0..nbrAngles).step(1) do |i| theta=360.0*i/nbrAngles res=forces.getR(theta) ld.setShellForces(res) res=moments.getR(theta) ld.setShellMoments(res) ... end # Angles loop
Then, the critical angle is identified and the corresponding Results are printed in the a result file.
The calculation has one additional parameter: “nbrAngles”, which corresponds to the number of rotation angles to be tested in the post-processing.
"testSat" method is slightly more complicated than before:
def testSat
db=LoadCases.getDb("LAUNCH")
GenPost::each do |current|
if current.respond_to?("preCalc") then
current.preCalc(db)
end
end
GC.start
version="All"
LoadCases.each(version) do |db,lcName,scName|
GenPost::each do |current|
if current.respond_to?("calcAll") then
current.calcAll(db,lcName,scName)
end
end
GC.start
end
db=LoadCases.getDb("LAUNCH")
GenPost::each do |current|
if current.respond_to?("postCalc") then
current.postCalc(db)
end
end
GC.start
end
The "GenPost" iterator is used to loop on the different object of class "GenPost" or of one of its derived classes. This iterator is called three times:
The first time "GenPost" iterator is used, one checks the existence of “preCalc” method in each object to perform preliminary operations before the loop on load case.
Then, the iterator is called inside the loop on load cases to perform the operations required for each load case.
The third time the iterator is called, this is done outside the load cases loop. Then the instance method "postCalc" is called to perform the operations that are to be done at the very end of the program. In the example, this operation corresponds to the printing of the maps of critical margins.
Note that “preCalc”, “calcAll” and “postCalc” methods are now instance methods. This means they are specific to a particular instance of the classes. Note also, that the availability of these instance methods is tested before the method is called.
The “testSat” example is defined in “testSat.rb” file. Similarly, a “dynam.rb” file is defined to provide an example for dynamic analysis. ‘dynam.rb” is very similar to “testSat.rb”, but the file calls another version of the LoadCases and includes other data for post-processing:
require "DATA/data_Post_accel" require "DATA/data_Post_cbush"
One should keep in mind that the data for dynamic Results post-processing are generally very different than the data for Static load cases post-processing. This justifies that separate “main” data files are written for these different categories of load cases.
Those data are very similar to those defined in “A” version of the post-processing. One added however, new methods to the “LoadCase” module to allow the post-processing of dynamic Results (SOL108 and SOL111 of Nastran).
In iterator “LoadCases::each”, a new proc object called “makeDynamLoop” loops on all the dynamic sub-cases (frequency outputs) for a given load case name. The three argument of this loop are
A String object containing the full name of the Nastran xdb file in which the dynamic Results will be read.
The Name of the Load Case for which Results shall be improved. This is also a String argument.
An integer argument corresponding to maximum number of dynamic sub-cases that can be stored in the DataBase. This parameter allows to prevent the DataBase memory to increase too much because it contains an excessive number of Results.
The first operation performed by “makeDynamLoop” is to build a list of sub-cases in sorted in order of increasing frequencies:
lcNames=[lcName]
tmpList={}
xdbInfos=db.getXdbLcInfos(fullXdbName)
xdbInfos.each do |info|
if (info[0]==lcName) then
tmpList[info[4]]=info[1]
end
end
scList=tmpList.sort
In the previous instructions, one first loads the information about load cases and sub-cases stored in the xdb Result file. Then, the sub-cases corresponding to the selected load case name are selected. Finally, they are sorted and stored in the Array “scList”.
Then, a loop is done on the list of sub-cases stored in “scList”. A new Array “scNames” containing a list of sub-cases is filled. Each time its size reaches the values specified by the proc argument, one reads the Results, yields them, and finally erases them from the DataBase. This is done as follows:
scNames=[]
scList.each do |intId,scName|
scNames << scName
if (scNames.size==maxScNbr) then
db.readXdb(fullXdbName,lcNames,scNames)
scNames.each do |name|
yield([db,lcName,name])
db.removeResults("SubCaseId",name)
GC.start
end
scNames=[]
end
end
At the end, the remaining sub-cases are calculated the same way:
db.readXdb(fullXdbName,lcNames,scNames)
scNames.each do |name|
yield([db,lcName,name])
db.removeResults("SubCaseId",name)
GC.start
end
GC.start
end
An example of use of the “makeDynamLoop” proc follows:
when "SINUS_Z" then
db=getDb("LAUNCH")
fullXdbName=getXdbDirName()+"/sol111_ri_xyz.xdb"
makeDynamLoop.call(fullXdbName,"SINUS_Z",30)
In this case, the Results of “SINUS_Z” load case are required, and the maximum number of sub-cases loaded simultaneously in the DataBase is 30. Note that this number should be chosen with care: if it is too small, many readings of the Nastran xdb file will be necessary which increases the disk access time. On the other hand, if the number is too big, a larger amount of memory might be necessary to store the Results in the DataBase. This is important if you have limited resources. It is the responsibility of “LoadCases” module manager to select an appropriate value of this integer parameter.
Note that we voluntarily limit the example of dynamic Results post-processing to a simple extraction from an xdb file. Actually, the possibilities of FeResPost are larger that. For example, it should be possible to read simultaneously the Results for different load cases as “SINUS_X”, “SINUS_Y” and “SINUS_Z” and to yield linear combinations of these elementary Results for the different frequency outputs.
One presents the example of data for honeycomb calculation. Also examples of data for dynamic post-processing with “PostExtract” class are presented.
The first operation consists in creating an instance object of class "PostCauchy":
require "post_Cauchy" post_honeycomb=PostCauchy.new
Then, three instance methods are created. For example, the "calcAll" method definition looks as follows:
def post_honeycomb.calcAll(db,lcName,scName) list = ["pan_MX_Honey_50", "pan_MY_Honey_50", ... end
One sees that the method is attached to the instance object created earlier, and not to its class.
The object also defines a "postCalc" method that defines several data and performs a call to writeGmshMinMosResults method:
def post_honeycomb.postCalc(db)
skeleton=Group.new
skeleton.setEntitiesByType("Element","Element 1:100000")
skeleton.matchWithDbEntities(db)
writeGmshMinMosResults(db,"OUT_STATICS/postSandwichHoney.gmsh",skeleton)
end
Note that object "post_skins" does not define the method "postCalc" and produces no Gmsh file.
In file “DATA/data_Post_TsaiHill.rb”, one defines the corresponding data for the calculation of Tsai-Hill criterion in panel -Z. Before doing a loop on the different load cases, one initializes the “@compDb” member data as follows:
def post_TsaiHill.preCalc(db) @compDb=db.getClaDb end
At the end of the calculations, the envelopes of Results and the mesh are printed:
def post_TsaiHill.postCalc(db)
skeleton=db.getGroupAllFEM()
writeGmshMinMosResults(db,"OUT_STATIC/postTsaiHill.gmsh",skeleton)
db.writeGmshMesh("OUT_STATIC/postTsaiHill.msh",0,skeleton)
end
A first instance of the “PostExtract” class is created. This instance is devoted to the printing of several nodal accelerations in Z direction. Basically, the method contains several calls to “calcOneGroup” method with the appropriate arguments that define the data:
def post_accel.calcAll(db,lcName,scName) resName="Accelerations (RI), translational" method="Nodes" csId=0 component="Z" calcOneGroup(db,lcName,scName,"Accel_Node_500001", "Node 500001", resName, method, csId, component) calcOneGroup(db,lcName,scName,"Accel_Node_20919", "Node 20919", resName, method, csId, component) calcOneGroup(db,lcName,scName,"Accel_Node_20920", "Node 20920", resName, method, csId, component) calcOneGroup(db,lcName,scName,"Accel_Node_40913", "Node 40913", resName, method, csId, component) ...
A second instance of the method is used to output the launcher interface force recovered from the corresponding CBUSH element=
def post_cbush.calcAll(db,lcName,scName) resName="Beam Forces (RI)" method="Elements" csId=0 component="XZ" calcOneGroup(db,lcName,scName,"Force_launcher", "Element 500003", resName, method, csId, component) end
Remember that the “calcAll” method is called for each load case or sub-case.
The final printing of values in “OUT_DYNAM” directory is called from “postCalc” method:
def post_accel.postCalc(db)
gnuplot("post_accel.dat")
end
When the post-processing is finished, and if you have gnuplot on your computer, you can visualize the values by entering the “OUT_DYNAM” directory and typing:
gnuplot < post_accel.dat gnuplot < post_cbush.dat
For example, the results obtained for the post-processing of CBUSH element forces are represented in Figure X.F.1 and X.F.2.
The data for the composite dynamic post-processing are defined in file
“DATA/data_Post_TsaiHillDynam.rb”. This file is very similar to the corresponding file for static
post-processing. Only one selects 12 sub-divisions for the rotation angles.
The “PostCauchy” class also defines two accelerated versions of the honeycomb and Von Mises criteria. These are defined by the “crit_HoneyAirbusAccel” and “crit_VonMisesAccel” methods of the class.
The data for the calculations of these versions of the criterion are defined in files “ DATA/data_Post_honeycomb2.rb” and “DATA/data_Post_skins2.rb”. The activation/deactivation of these calculations can be obtained by uncommenting or commenting the corresponding require statements in “testSat.rb” file:
require "DATA/loadCases" require "DATA/data_Post_Interf" require "DATA/data_Post_honeycomb" #~ require "DATA/data_Post_honeycomb2" require "DATA/data_Post_skins" #~ require "DATA/data_Post_skins2" require "DATA/data_Post_TsaiHill"
We advise the use to play with the example and try to understand it. This post-processing program architecture is very flexible and should allow the developments of very sophisticated and powerful tools.
The example “dynam.rb” illustrating the post-processing of dynamic Complex Results is very preliminary and can be improved in several ways:
The excitation on the large mass below the satellite corresponds to a sinusoidal acceleration of amplitude 1 . This is not a realistic case. Actually, a realistic excitation should be a data of the post-processing. For this, the post-processing should be modified.
One should try to program with Ruby and FeResPost a tool similar to the Patran tool MSC.Random to calculate the response of structures to random excitations.
...
The description of FeResPost COM component in Part VI, and the corresponding examples in Part VII might suggest that the only way to use FeResPost in excel is to write VBA modules that use FeResPost COM component.
It is not true. One explains in this Appendix, how ruby can be embedded into excel, and how VBA calls may be marshaled to ruby interpreter. Then, the programming of post-processing can be done nearly entirely with ruby language and FeResPost ruby extension may be used instead of the COM component.
The technique we propose here makes use of excel/VBA capability to load dll libraries and of ruby language to be dynamically embedded into another application by loading the ruby interpreter dynamic library. A schematic representation of the process is given in Figure X.G.1:
Excel and its objects (workbooks, worksheets, ranges, automation buttons...) are represented in blue.
The green part corresponds to the small bits of VBA code that is necessary to call the ruby runtime environment through the bridge.
The parts specific to the bridging are represented in red. In the excel process, they correspond to the two loaded dynamic libraries (the bridging and the ruby runtime environment, and their different interactions. Outside excel process, the external environment corresponds to ruby programs, loaded extensions, input and output files...
In order to explain how the bridging works, one gives in section X.G.1.1 information about the programming of the bridge. In section X.G.2.1 one explains what is done in excel VBA modules to use the bridge and ruby programs.
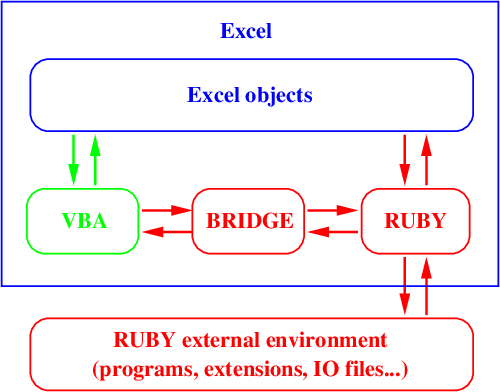

The sources are made of three C++ “cpp” files, three C++ header files and one “def” file that defines the four functions that will be exported into the dll library. More precisely:
Files “conversion.h” and “conversion.cpp” are devoted to type conversion between VBA and ruby. More precisely, the corresponding “convert” C++ methods perform conversions between VBA “Variant” and ruby “VALUE” types. Note that conversion are done from Variant to VALUE, or in the other direction. Some “convert” methods from Variant to other C++ types are also defined for internal use only.
“win32ole.h” and “win32ole.cpp” define methods that are called from “conversion.cpp” functions. They contain specifics to the conversion of COM automation types. The reason why these methods have been kept separate from the conversion ones, is that the bits of code in our “win32ole” files have been extracted from the corresponding sources of ruby “win32ole” extension.
Files “marshal.h” and “marshal.cpp” contain the definition of methods that dispatch the calls from VBA to ruby. In particular, four methods that are meant to be exported in the dll library are defined here.
File “marshal.def” exports the methods that will be used in excel: “RubyInit”, “RubyFinish”, “RubyRequire”, “RubyLoad” and “RubyCallMethod”. The “RubyInit” method has no argument and simply initializes the ruby runtime. The “RubyFinish” method is used to quit ruby interpreter and unload the bridge library. Methods “RubyRequire” and “RubyLoad” can be used to load the ruby programs that shall later be called from VBA. Each of these two methods has one argument corresponding to the name of the ruby file to be imported. Finally, method “RubyCallMethod” is the one that really performs the dispatch between VBA and ruby. The method has four arguments that correspond to the methods receiver (module or class name), the name of the method, an Array containing the arguments, and the Variant in which the value returned by the method shall be stored. The four methods listed above return an integer containing the error code.
Note that the four arguments of the method “RubyCallMethod” are pointers to VARIANT objects:
extern "C" int __stdcall RubyCallMethod(const VARIANT *objName,
const VARIANT *methodName,const VARIANT *args,
VARIANT *ret) {
...
}
One remarks that the bridge between VBA and ruby implicitly assumes that the ruby “win32ole” extension is present. (This extension is required in the “RubyInit” method.) It was not a priori mandatory. However, the early loading of “win32ole” extension helps the programming of the for COM automation types translations. As the manipulation of these types by ruby programs might be necessary, it is necessary to load the extension as early as possible. This means that the ruby distribution with which the bridge is used must contain the “win32ole” extension. (Of course, the bridge should be used only on Windows platforms on which Office is installed.)
The compilation of the library is straightforward. On my computer, it looks like this:
g++ -O2 -IC:/NewProgs/RUBY/Ruby187/lib/ruby/1.8/i386-mingw32 \ -c marshal.cpp g++ -O2 -IC:/NewProgs/RUBY/Ruby187/lib/ruby/1.8/i386-mingw32 \ -c conversion.cpp g++ -O2 -IC:/NewProgs/RUBY/Ruby187/lib/ruby/1.8/i386-mingw32 \ -c win32ole.cpp gcc -O2 -LC:/NewProgs/RUBY/Ruby187/bin \ -fPIC -shared -static -m32 -Wl,--enable-auto-import \ marshal.o conversion.o win32ole.o -lmsvcrt-ruby18 \ -lws2_32 -luuid -lole32 -loleaut32 -lstdc++ -lm \ marshal.def -o vbaruby.dll
Note that the “vbaruby.dll” is linked to the “msvcrt-ruby18.dll” dynamic library. This means that the ruby runtime library is automatically loaded into excel when “vbaruby.dll” is loaded. This also means that “msvcrt-ruby18.dll” must be located in a directory defined in the “PATH” environment variable. Also, the “vbaruby.dll” library is linked to a particular version of ruby runtime library. If another version of ruby is installed, the bridge may have to be re-compiled.
One summarizes here the requirements to use the VBA-ruby bridge:
The bridge works on Windows platforms only.
It must be used from VBA environment. Typically, it shall be used in excel.
the “win32ole” ruby extension must be available.
The dll library is linked to a peculiar version of ruby runtime machine. This means that this version of the runtime must be available, and the corresponding “bin” directory must be in the “PATH” environment variable. If someone wants to use another version of the ruby runtime machine, then the bridge must be recompiled.
Some of the practical details for using the bridge are explained in the example in section X.G.2.
Note that the installation of FeResPost is not a requirement for the use of VBA-ruby bridge. Indeed the bridge is independent of FeResPost and can be used for any ruby post-processing.
One presents in directory “TESTSAT/VBARUBYEX” an example that corresponds to the “PostProject.xlsm” example illustrating FeResPost COM component. (See section VII.4.) The programming of ruby modules is discussed in section X.G.2.1. Two VBA modules are defined in the excel workbook: “RubyMarshal” and “RubyFunctions”. These modules are discussed in section X.G.2.2 and section X.G.2.3 respectively. A few other points are discussed in section X.G.2.4.
In this case, most of the VBA programming of post-processing operations has been replaced by corresponding code in “TESTSAT/VBARUBYEX/RUBY” directory. This code is loaded through the “main.rb” main file. This file looks as follows:
$: << Dir.getwd+"/RUBY"
$: << "D:/SHARED/FERESPOST/SRC/OUTPUTS/RUBY"
$: << "D:/FERESPOST/BINARIES/FeResPost_4.0.10/RUBY"
$stdout.reopen("main.log","w")
$stdout.sync=true
$stderr=$stdout
require "dl"
require "UTIL/util"
require "UTIL/xls"
require "POSTPROJECT/postProject"
One makes the following comments:
The first lines update the list of directories from which ruby files and extensions shall be loaded. You must change these lines according to the local configuration of your computer. Note that the first directory added to the list is defined relative to the current working directory. The rest of the programming assumes that the working directory is the one in which “PostProject.xlsm” is located. A special VBA command in “PostProject.xlsm” has been added to ensure it is the case.
The following lines redirect standard outputs to “main.log” file. This can be handy when you have a bug and you want to retrieve ruby error messages.
Finally, the lines that follow perform “require” statements that load the programmed modules. The “postProject” require corresponds to most of the post-processing programming.
Note that the example we provide here depends on the availability of “FeResPost” and “sqlite3” ruby extensions. The example will not work on your computer if these two modules are not properly installed.
This VBA module performs the loading of dynamic libraries, and defines methods that can be called from anywhere in the VBA code and that dispatch the calls to corresponding ruby methods. The code begins as follows:
Const vbaRubyLib As String = _ "D:\SHARED\FERESPOST\SRC\OUTPUTS\VBARUBY\vbaruby.dll" ’ Private Declare Function LoadLibrary Lib "kernel32" _ Alias "LoadLibraryA" (ByVal lpLibFileName As String) As Long Private Declare Function FreeLibrary Lib "kernel32" _ (ByVal hLibModule As Long) As Long ’ Public Declare Function RubyInit _ Lib "vbaruby" () As Long Public Declare Function RubyFinish _ Lib "vbaruby" () As Long Public Declare Function RubyRequire _ Lib "vbaruby" (ByVal param As Long) As Long Public Declare Function RubyLoad _ Lib "vbaruby" (ByVal param As Long) As Long Public Declare Function RubyCallMethod _ Lib "vbaruby" (ByVal objName As Long, _ ByVal methodName As Long, ByVal args As Long, _ ByVal ret As Long) As Long ’ Private testLibrary As Long
In this library:
The constant “vbaRubyLib” contains the full path to bridge dynamic library. You will probably have to change this line to match the configuration of your computer.
Two methods from “kernel32” system library are declared. These methods are used to load and free libraries.
Five methods from the “vbaruby” bridge dll library are declared. Those are the methods that perform the marshaling between VBA and ruby. Note that all the parameters are long integers; these correspond to pointers towards the corresponding VARIANT objects.
Variable “testLibrary” contains a pointer to the bridge library.
The VBA procedure “libInit” performs the loading of the bridge library and the require statement to ruby main file:
Public Sub libInit() Dim rbFile As Variant If testLibrary = 0 Then testLibrary = LoadLibrary(vbaRubyLib) RubyInit End If rbFile = ThisWorkbook.Path + "\RUBY\main.rb" RubyRequire VarPtr(rbFile) End Sub
Note that the path to the main required ruby be file is defined in the subroutine. Other choices are possible. You can change the way of accessing the ruby programs according to your preferences.
The VBA function “CallMethod” calls the bridge method “RubyCallMethod”. Its three arguments are the receiver of the method call (the name of a volume or of a class), the name of the method, and a ParamArray VARIANT argument containing an optional number of arguments.
Public Function CallMethod(obj As String, method As String, _ ParamArray args() As Variant) As Variant Dim varObj As Variant, varMethod As Variant, _ varArgs As Variant, ret As Variant Dim var As Variant ’ varObj = obj varMethod = method varArgs = args ’ RubyCallMethod VarPtr(varObj), VarPtr(varMethod), _ VarPtr(varArgs), VarPtr(ret) CallMethod = ret End Function
Note that the arguments passed to the “RubyCallMethod” in bridge library are pointers to VARIANT objects. These pointers are obtained by calls to “VbaPtr” function. The last argument of call to “RubyCallMethod” is a pointer to “ret” VARIANT that shall contain the value returned by the called ruby method. Note that the creation of pointers to VARIANT arguments and the call to “RubyCallMethod” bridge function are the main things done by the function.
Note also that the solution one proposes allows to call methods defined in modules, or class methods. It is not possible to directly call methods on instances of a class.
A “CallMethodValue” method is also defined in “RubyMarshal” VBA module. This method is very similar to “CallMethod”. The difference is that each time a “Range” argument is found, it is replaced by an Array containing the correspond Cell values.
One defines in “RubyFunctions” VBA module functions and subroutines that can be called from other VBA modules, or directly used as formulas in spreadsheets. For example, the function “getParameter” returns a parameter calculated from the load case name, and the parameter name:
Function getParameter(lcName As String, paramName As String)
getParameter = CallMethodValue("PostProject::DbAndLoadCases", _
"getParameter", lcName, paramName)
End Function
The function “getShellVonMisesMax” calculates the maximum von Mises stress on a Group of shell elements:
Function getShellVonMisesMax(lcName As String, method As String, _ groupName As String, Optional gmshFileName As String = "", _ Optional gmshResName As String = "") As Variant getShellVonMisesMax = CallMethodValue( _ "PostProject::ExtractionCriteria", _ "getShellVonMisesMax", lcName, method, groupName, _ gmshFileName, gmshResName) End Function
Note that the ruby methods called from VBA may also correspond to subroutines, even though the distinction between subroutines and functions do not exist in ruby. Examples, of calls to subroutines can be found in the VBA code corresponding to “LcSelector” spreadsheet. For example, one presents below the code associated to the button “ReadDbAndLoadCases” in the spreadsheet:
Public Sub ReadDbAndLoadCases_Click()
On Error GoTo locError:
’
Dim x As Variant
x = CallMethod("PostProject::DbAndLoadCases", _
"setWorkbook", ThisWorkbook)
x = CallMethodValue("PostProject::DbAndLoadCases", _
"readDbAndLoadCases", ActiveSheet.name, nbrReservedLines, _
LcSelect)
Exit Sub
’
locError:
MsgBox prompt:="Something wrong happened! check standard output file.", _
Title:="ReadDbAndLoadCases_Click()"
MsgBox prompt:=CurDir, Title:=CurDir()
End Sub
In the “ThisWorkbook” VBA code, two excel event subroutines are provided. When opening, the event “Workbook_Open” changes the excel execution directory to the directory containing the workbook, loads the vbaruby bridge library and initializes ruby by calling “libInit”, then calls the “PostProject::DbAndLoadCases::setWorkbook” method to initialize the corresponding variable of the ruby post-processing program:
Sub Workbook_Open()
ChDrive (Left(ActiveWorkbook.Path, 1))
ChDir (ActiveWorkbook.Path)
Application.Calculation = xlCalculationAutomatic
Call libInit
Dim x As Variant
x = CallMethod("PostProject::DbAndLoadCases", "setWorkbook", ThisWorkbook)
End Sub
This step is mandatory if one wants the “main.rb” file to be loaded correctly, because a path relative to the directory containing “PostProject.xlsm” is used in the “RubyMarshal” VBA module. (Sees section X.G.2.2.) It also ensures that the “main.log” file to which ruby standard output is redirected is located in the same directory as “PostProject.xlsm”. (See section X.G.2.1.)
When closing the excel workbook, the following method is called:
Sub workbook_BeforeClose(cancel As Boolean)
Application.Calculation = xlCalculationAutomatic
Dim x As Variant
x = CallMethodValue("PostProject", "clearModuleVariables")
End Sub
This method is meant, among other things, to remove all references to excel automation objects, so that the closing of the application is cleanly done. Practically, it sometimes fail, so that you have to kill excel with the task manager. (If someone can explain me why...)
In order to adapt the example to your configuration you must:
Change the “vbaRubyLib” constant in “RubyMarshall” Module of the excel spreadsheet.
Change the “PATH” environment variable so that it points to the “bin” directory of the particular version you intend to use.
In “RUBY/main.rb” file, change the include directory definition:
$: << "D:/SHARED/FERESPOST/SRC/OUTPUTS/RUBY_191"
Sometimes, the finite element model of part of a structure does not allow to obtain reliable estimates of connection loads. This is the case for example:
When RBE2 or RBE3 elements are used to distribute connection loads on a larger area of the model.
When very stiff and coarsely modeled parts are assembled together.
When thermo-elastic environments lead to unrealistic reactions in connections.
...
Then, bolt group re-distributions allow to produce smoother distribution of connection loads from an initial distribution produced by FEM solver.
We present here the equations that govern the redistribution of loads on a bolt group. The equations are inspired by similar equations developed in [eEL94] for the calculation of a solid motion.
We make several assumptions to simplify the developments that follow:
All the developements are done considering Cartesian coordinate systems. If the finite element model produces results in other type of coordinate systems, these results (forces, moments and coordinates) must be expressed in a Cartesian coordinate system before performing the bolt group calculations.
The global force and moment transferred by the group of connections is noted by and respectively. These vectors are defined wrt to bolt group center of gravity that will be defined later.
the two parts assembled by a group of connections are assumed infinitely stiff compared to the connections. The only source of flexibility of the assembly is the set of connections.
Each connection of the group is characterized by two scalar stiffnesses: a translational one and a rotational one. These stiffnesses are noted and respectively. We will see below that this assumption is a simplification of a general case.
The behaviour of each connection in the group is linear. The same is then true for the group of connections global behaviour.
Each connection is also characterized by its location in bolt group local coordinate system. Bolt coordinates are noted in which index corresponds to the three position components and index loops on the connections of the group ().
Bolt group local coordinate system is parallel to connection loads extraction coordinate system, but its origin is located as the bolt group center of gravity.
The calculation of bolt group center of gravity is made easier by the fact that connection translational stifnesses are scalar. If connection coordinates in the initial extraction Cartesian coordinate system are noted , center of gravity is calculated as follows:
|
| (X.H.1) |
Note that this simplification is possible only because connection translational stiffnesses are scalar (isotropy assumption). Once the center of gravity has been calculated, a new Cartesian coordinate system parallel to the initial one and with origin as center of gravity is defined. In this translated coordinate system, connection locations are simply calculated as:
|
| (X.H.2) |
and all the following calculations will be done using these coordinates.
Note that the definition of a bolt group center of gravity is possible only because connection stiffnesses are scalar. Otherwsie, a different center of gravity would be calculated for each direction. Actually, it would be even worse that that: the deformation of the assembly in one direction could lead to a global force with a different direction. This means that no center of gravity could be calculated.
The total force and moment transmitted by an interface are calculated as follows:
|
| (X.H.3) |
|
| (X.H.4) |
in which and are the connection loads extracted from FEM results before bolt group redistribution.
We have seen in section X.H.1 that the parts are assumed infinitely stiff compared to the conenctions. The only source of flexibility in the assembly is the flexibility of connections. Here, to fix the ideas, we consider that part “A” is fixed, and that only part “B” moves slightly. This means that only the motions of part “B” must be considered in the development of expressions leading to the estimation of group global stiffnesses.
As part “B” is rigid, its motion can be characterized by a vectorial translation and a vectorial rotation of components and respectively. These components are expressed in bolt group center of gravity Cartesian coordinate system defined in section X.H.2. The motion of “B” side of connection is then
|
|
in which we use the Bose-Einstein convention for the notation of components, except that no distinction is done between the covariant and contravariant types of components as coordinate system is a Cartesian one. Previous expression can also simply be written:
|
| (X.H.5) |
This equation shows that the translational elongation of each connection depends on its location wrt bolt group center of gravity. On the other hand, all the rotational deformations are exactly equal to part “B” global rotation:
|
| (X.H.6) |
To these connection deformations correspond connection forces and moments:
|
| (X.H.7) |
|
| (X.H.8) |
With these expressions for connection deformations, bolt group total strain energy can be developed as follows:
In last expression, one term has been set to zero because (origin of coordinate system located at bolt group center of gravity). Finally, one develops this expression following similar development for the definition of interia tensor in chapter 32 of [eEL94]:
Last expression allows us to introduce one scalar and one tensorial quantities characterizing bolt group total stiffness:
|
| (X.H.11) |
|
| (X.H.12) |
The scalar quantity corresponds to a interface global translational stiffness. The tensorial quantity is the interface total rotational stiffness. Using these expressions, the bolt group strain energy is given by
|
|
The strain energy is also given by:
|
|
This allows to write an expression that relates the interface global force and moment to interface deformation:
|
|
that can be inverted as follows:
|
| (X.H.13) |
We have assumed here that can be inverted.
The equations developed in section X.H.2 allow the definition of the different steps involved in bolt group redistribution of connection loads. We summarizes these steps below:
Bolt group center of gravity is calculated using (X.H.1).
This allows to calculate connection locations in a new coordinate system with origin on this center of gravity using expression (X.H.2)
The bolt group global stiffnesses and are calculated with expressions (X.H.11) and (X.H.12) respectively.
The compliance matrix in (X.H.13) can then be calculated. Let us remark that so far, the calculations do not depend on connection loads. This means that they can be performed only once before the actual post-processing of FEM results.
For a given load case, connection loads and can be extracted from the soler result file.
Bolt group global forces and moments are then calculated with (X.H.3) and (X.H.4).
Expression (X.H.13) is used to calculated bolt group global translational and rotational deformation.
Connection forces and moments are then calculated with expressions (X.H.7) and (X.H.8).
The values atributed to connection translational stiffness can be an issue. Generally test results are not available. The estimation of connection stiffness via detailed FEM is a possibility, but this might prove very complicated and expensive. One notices however, that as far as the distributed loads are concerned, only the relative stiffnessesz of the different connections in an interface matter. This means that if all connections have common characteristics, the use of any common value for stiffnesses will lead to the same results. If bolt group involves several types of connections, the stiffnesses considered in the calculations should be estimated using reasonable assumptions. For example, one can consider a proportionality to bolt section area of the kind , in which is the nominal diamter of connection .
The bolt group equations that are developed in this Appendix consider connections that have translational and rotational stiffnesses. In many case, the rotational stiffness is not necessary to redistribute interface loads. Setting will lead to a redistribution in which the connections of the interface are loaded with forces only (). This approach works only when setting does not lead to a singular matrix . This will be the case when interface connections are not aligned along a straight line. Would the connections be distributed along a straight line, and the particular case of a group of two connections saisfies this condition, a rotational stiffness must be attributed to connections to allow a bolt group redistribution.
Then appears the issue of the rotational stiffness to be attributed to the connections. As test results are generally not available, we advice to put a rotational stiffness corresponding approximately to .
Copyright 2005-2024 Renaud Sizaire
This document is the User Manual of FeResPost.
FeResPost is free software; you can redistribute it and/or modify it under the terms of the GNU Lesser General Public License as published by the Free Software Foundation; either version 3 of the License, or (at your option) any later version.
FeResPost is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU Lesser General Public License for more details.
You should have received a copy of the GNU Lesser General Public License along with FeResPost; if not, write to the Free Software Foundation, Inc., 59 Temple Place, Suite 330, Boston, MA 02111-1307 USA
GNU GENERAL PUBLIC LICENSE Version 3, 29 June 2007
Copyright © 2007 Free Software Foundation, Inc. http://fsf.org/
Everyone is permitted to copy and distribute verbatim copies of this
license document, but changing it is not allowed.
The GNU General Public License is a free, copyleft license for software and other kinds of works.
The licenses for most software and other practical works are designed to take away your freedom to share and change the works. By contrast, the GNU General Public License is intended to guarantee your freedom to share and change all versions of a program–to make sure it remains free software for all its users. We, the Free Software Foundation, use the GNU General Public License for most of our software; it applies also to any other work released this way by its authors. You can apply it to your programs, too.
When we speak of free software, we are referring to freedom, not price. Our General Public Licenses are designed to make sure that you have the freedom to distribute copies of free software (and charge for them if you wish), that you receive source code or can get it if you want it, that you can change the software or use pieces of it in new free programs, and that you know you can do these things.
To protect your rights, we need to prevent others from denying you these rights or asking you to surrender the rights. Therefore, you have certain responsibilities if you distribute copies of the software, or if you modify it: responsibilities to respect the freedom of others.
For example, if you distribute copies of such a program, whether gratis or for a fee, you must pass on to the recipients the same freedoms that you received. You must make sure that they, too, receive or can get the source code. And you must show them these terms so they know their rights.
Developers that use the GNU GPL protect your rights with two steps: (1) assert copyright on the software, and (2) offer you this License giving you legal permission to copy, distribute and/or modify it.
For the developers’ and authors’ protection, the GPL clearly explains that there is no warranty for this free software. For both users’ and authors’ sake, the GPL requires that modified versions be marked as changed, so that their problems will not be attributed erroneously to authors of previous versions.
Some devices are designed to deny users access to install or run modified versions of the software inside them, although the manufacturer can do so. This is fundamentally incompatible with the aim of protecting users’ freedom to change the software. The systematic pattern of such abuse occurs in the area of products for individuals to use, which is precisely where it is most unacceptable. Therefore, we have designed this version of the GPL to prohibit the practice for those products. If such problems arise substantially in other domains, we stand ready to extend this provision to those domains in future versions of the GPL, as needed to protect the freedom of users.
Finally, every program is threatened constantly by software patents. States should not allow patents to restrict development and use of software on general-purpose computers, but in those that do, we wish to avoid the special danger that patents applied to a free program could make it effectively proprietary. To prevent this, the GPL assures that patents cannot be used to render the program non-free.
The precise terms and conditions for copying, distribution and modification follow.
_______________________________________________________________________________________________________________________________________________________
TERMS AND CONDITIONS
Definitions.
“This License” refers to version 3 of the GNU General Public License.
“Copyright” also means copyright-like laws that apply to other kinds of works, such as semiconductor masks.
“The Program” refers to any copyrightable work licensed under this License. Each licensee is addressed as “you”. “Licensees” and “recipients” may be individuals or organizations.
To “modify” a work means to copy from or adapt all or part of the work in a fashion requiring copyright permission, other than the making of an exact copy. The resulting work is called a “modified version” of the earlier work or a work “based on” the earlier work.
A “covered work” means either the unmodified Program or a work based on the Program.
To “propagate” a work means to do anything with it that, without permission, would make you directly or secondarily liable for infringement under applicable copyright law, except executing it on a computer or modifying a private copy. Propagation includes copying, distribution (with or without modification), making available to the public, and in some countries other activities as well.
To “convey” a work means any kind of propagation that enables other parties to make or receive copies. Mere interaction with a user through a computer network, with no transfer of a copy, is not conveying.
An interactive user interface displays “Appropriate Legal Notices” to the extent that it includes a convenient and prominently visible feature that (1) displays an appropriate copyright notice, and (2) tells the user that there is no warranty for the work (except to the extent that warranties are provided), that licensees may convey the work under this License, and how to view a copy of this License. If the interface presents a list of user commands or options, such as a menu, a prominent item in the list meets this criterion.
Source Code.
The “source code” for a work means the preferred form of the work for making modifications to it. “Object code” means any non-source form of a work.
A “Standard Interface” means an interface that either is an official standard defined by a recognized standards body, or, in the case of interfaces specified for a particular programming language, one that is widely used among developers working in that language.
The “System Libraries” of an executable work include anything, other than the work as a whole, that (a) is included in the normal form of packaging a Major Component, but which is not part of that Major Component, and (b) serves only to enable use of the work with that Major Component, or to implement a Standard Interface for which an implementation is available to the public in source code form. A “Major Component”, in this context, means a major essential component (kernel, window system, and so on) of the specific operating system (if any) on which the executable work runs, or a compiler used to produce the work, or an object code interpreter used to run it.
The “Corresponding Source” for a work in object code form means all the source code needed to generate, install, and (for an executable work) run the object code and to modify the work, including scripts to control those activities. However, it does not include the work’s System Libraries, or general-purpose tools or generally available free programs which are used unmodified in performing those activities but which are not part of the work. For example, Corresponding Source includes interface definition files associated with source files for the work, and the source code for shared libraries and dynamically linked subprograms that the work is specifically designed to require, such as by intimate data communication or control flow between those subprograms and other parts of the work.
The Corresponding Source need not include anything that users can regenerate automatically from other parts of the Corresponding Source.
The Corresponding Source for a work in source code form is that same work.
Basic Permissions.
All rights granted under this License are granted for the term of copyright on the Program, and are irrevocable provided the stated conditions are met. This License explicitly affirms your unlimited permission to run the unmodified Program. The output from running a covered work is covered by this License only if the output, given its content, constitutes a covered work. This License acknowledges your rights of fair use or other equivalent, as provided by copyright law.
You may make, run and propagate covered works that you do not convey, without conditions so long as your license otherwise remains in force. You may convey covered works to others for the sole purpose of having them make modifications exclusively for you, or provide you with facilities for running those works, provided that you comply with the terms of this License in conveying all material for which you do not control copyright. Those thus making or running the covered works for you must do so exclusively on your behalf, under your direction and control, on terms that prohibit them from making any copies of your copyrighted material outside their relationship with you.
Conveying under any other circumstances is permitted solely under the conditions stated below. Sublicensing is not allowed; section 10 makes it unnecessary.
Protecting Users’ Legal Rights From Anti-Circumvention Law.
No covered work shall be deemed part of an effective technological measure under any applicable law fulfilling obligations under article 11 of the WIPO copyright treaty adopted on 20 December 1996, or similar laws prohibiting or restricting circumvention of such measures.
When you convey a covered work, you waive any legal power to forbid circumvention of technological measures to the extent such circumvention is effected by exercising rights under this License with respect to the covered work, and you disclaim any intention to limit operation or modification of the work as a means of enforcing, against the work’s users, your or third parties’ legal rights to forbid circumvention of technological measures.
Conveying Verbatim Copies.
You may convey verbatim copies of the Program’s source code as you receive it, in any medium, provided that you conspicuously and appropriately publish on each copy an appropriate copyright notice; keep intact all notices stating that this License and any non-permissive terms added in accord with section 7 apply to the code; keep intact all notices of the absence of any warranty; and give all recipients a copy of this License along with the Program.
You may charge any price or no price for each copy that you convey, and you may offer support or warranty protection for a fee.
Conveying Modified Source Versions.
You may convey a work based on the Program, or the modifications to produce it from the Program, in the form of source code under the terms of section 4, provided that you also meet all of these conditions:
The work must carry prominent notices stating that you modified it, and giving a relevant date.
The work must carry prominent notices stating that it is released under this License and any conditions added under section 7. This requirement modifies the requirement in section 4 to “keep intact all notices”.
You must license the entire work, as a whole, under this License to anyone who comes into possession of a copy. This License will therefore apply, along with any applicable section 7 additional terms, to the whole of the work, and all its parts, regardless of how they are packaged. This License gives no permission to license the work in any other way, but it does not invalidate such permission if you have separately received it.
If the work has interactive user interfaces, each must display Appropriate Legal Notices; however, if the Program has interactive interfaces that do not display Appropriate Legal Notices, your work need not make them do so.
A compilation of a covered work with other separate and independent works, which are not by their nature extensions of the covered work, and which are not combined with it such as to form a larger program, in or on a volume of a storage or distribution medium, is called an “aggregate” if the compilation and its resulting copyright are not used to limit the access or legal rights of the compilation’s users beyond what the individual works permit. Inclusion of a covered work in an aggregate does not cause this License to apply to the other parts of the aggregate.
Conveying Non-Source Forms.
You may convey a covered work in object code form under the terms of sections 4 and 5, provided that you also convey the machine-readable Corresponding Source under the terms of this License, in one of these ways:
Convey the object code in, or embodied in, a physical product (including a physical distribution medium), accompanied by the Corresponding Source fixed on a durable physical medium customarily used for software interchange.
Convey the object code in, or embodied in, a physical product (including a physical distribution medium), accompanied by a written offer, valid for at least three years and valid for as long as you offer spare parts or customer support for that product model, to give anyone who possesses the object code either (1) a copy of the Corresponding Source for all the software in the product that is covered by this License, on a durable physical medium customarily used for software interchange, for a price no more than your reasonable cost of physically performing this conveying of source, or (2) access to copy the Corresponding Source from a network server at no charge.
Convey individual copies of the object code with a copy of the written offer to provide the Corresponding Source. This alternative is allowed only occasionally and noncommercially, and only if you received the object code with such an offer, in accord with subsection 6b.
Convey the object code by offering access from a designated place (gratis or for a charge), and offer equivalent access to the Corresponding Source in the same way through the same place at no further charge. You need not require recipients to copy the Corresponding Source along with the object code. If the place to copy the object code is a network server, the Corresponding Source may be on a different server (operated by you or a third party) that supports equivalent copying facilities, provided you maintain clear directions next to the object code saying where to find the Corresponding Source. Regardless of what server hosts the Corresponding Source, you remain obligated to ensure that it is available for as long as needed to satisfy these requirements.
Convey the object code using peer-to-peer transmission, provided you inform other peers where the object code and Corresponding Source of the work are being offered to the general public at no charge under subsection 6d.
A separable portion of the object code, whose source code is excluded from the Corresponding Source as a System Library, need not be included in conveying the object code work.
A “User Product” is either (1) a “consumer product”, which means any tangible personal property which is normally used for personal, family, or household purposes, or (2) anything designed or sold for incorporation into a dwelling. In determining whether a product is a consumer product, doubtful cases shall be resolved in favor of coverage. For a particular product received by a particular user, “normally used” refers to a typical or common use of that class of product, regardless of the status of the particular user or of the way in which the particular user actually uses, or expects or is expected to use, the product. A product is a consumer product regardless of whether the product has substantial commercial, industrial or non-consumer uses, unless such uses represent the only significant mode of use of the product.
“Installation Information” for a User Product means any methods, procedures, authorization keys, or other information required to install and execute modified versions of a covered work in that User Product from a modified version of its Corresponding Source. The information must suffice to ensure that the continued functioning of the modified object code is in no case prevented or interfered with solely because modification has been made.
If you convey an object code work under this section in, or with, or specifically for use in, a User Product, and the conveying occurs as part of a transaction in which the right of possession and use of the User Product is transferred to the recipient in perpetuity or for a fixed term (regardless of how the transaction is characterized), the Corresponding Source conveyed under this section must be accompanied by the Installation Information. But this requirement does not apply if neither you nor any third party retains the ability to install modified object code on the User Product (for example, the work has been installed in ROM).
The requirement to provide Installation Information does not include a requirement to continue to provide support service, warranty, or updates for a work that has been modified or installed by the recipient, or for the User Product in which it has been modified or installed. Access to a network may be denied when the modification itself materially and adversely affects the operation of the network or violates the rules and protocols for communication across the network.
Corresponding Source conveyed, and Installation Information provided, in accord with this section must be in a format that is publicly documented (and with an implementation available to the public in source code form), and must require no special password or key for unpacking, reading or copying.
Additional Terms.
“Additional permissions” are terms that supplement the terms of this License by making exceptions from one or more of its conditions. Additional permissions that are applicable to the entire Program shall be treated as though they were included in this License, to the extent that they are valid under applicable law. If additional permissions apply only to part of the Program, that part may be used separately under those permissions, but the entire Program remains governed by this License without regard to the additional permissions.
When you convey a copy of a covered work, you may at your option remove any additional permissions from that copy, or from any part of it. (Additional permissions may be written to require their own removal in certain cases when you modify the work.) You may place additional permissions on material, added by you to a covered work, for which you have or can give appropriate copyright permission.
Notwithstanding any other provision of this License, for material you add to a covered work, you may (if authorized by the copyright holders of that material) supplement the terms of this License with terms:
Disclaiming warranty or limiting liability differently from the terms of sections 15 and 16 of this License; or
Requiring preservation of specified reasonable legal notices or author attributions in that material or in the Appropriate Legal Notices displayed by works containing it; or
Prohibiting misrepresentation of the origin of that material, or requiring that modified versions of such material be marked in reasonable ways as different from the original version; or
Limiting the use for publicity purposes of names of licensors or authors of the material; or
Declining to grant rights under trademark law for use of some trade names, trademarks, or service marks; or
Requiring indemnification of licensors and authors of that material by anyone who conveys the material (or modified versions of it) with contractual assumptions of liability to the recipient, for any liability that these contractual assumptions directly impose on those licensors and authors.
All other non-permissive additional terms are considered “further restrictions” within the meaning of section 10. If the Program as you received it, or any part of it, contains a notice stating that it is governed by this License along with a term that is a further restriction, you may remove that term. If a license document contains a further restriction but permits relicensing or conveying under this License, you may add to a covered work material governed by the terms of that license document, provided that the further restriction does not survive such relicensing or conveying.
If you add terms to a covered work in accord with this section, you must place, in the relevant source files, a statement of the additional terms that apply to those files, or a notice indicating where to find the applicable terms.
Additional terms, permissive or non-permissive, may be stated in the form of a separately written license, or stated as exceptions; the above requirements apply either way.
Termination.
You may not propagate or modify a covered work except as expressly provided under this License. Any attempt otherwise to propagate or modify it is void, and will automatically terminate your rights under this License (including any patent licenses granted under the third paragraph of section 11).
However, if you cease all violation of this License, then your license from a particular copyright holder is reinstated (a) provisionally, unless and until the copyright holder explicitly and finally terminates your license, and (b) permanently, if the copyright holder fails to notify you of the violation by some reasonable means prior to 60 days after the cessation.
Moreover, your license from a particular copyright holder is reinstated permanently if the copyright holder notifies you of the violation by some reasonable means, this is the first time you have received notice of violation of this License (for any work) from that copyright holder, and you cure the violation prior to 30 days after your receipt of the notice.
Termination of your rights under this section does not terminate the licenses of parties who have received copies or rights from you under this License. If your rights have been terminated and not permanently reinstated, you do not qualify to receive new licenses for the same material under section 10.
Acceptance Not Required for Having Copies.
You are not required to accept this License in order to receive or run a copy of the Program. Ancillary propagation of a covered work occurring solely as a consequence of using peer-to-peer transmission to receive a copy likewise does not require acceptance. However, nothing other than this License grants you permission to propagate or modify any covered work. These actions infringe copyright if you do not accept this License. Therefore, by modifying or propagating a covered work, you indicate your acceptance of this License to do so.
Automatic Licensing of Downstream Recipients.
Each time you convey a covered work, the recipient automatically receives a license from the original licensors, to run, modify and propagate that work, subject to this License. You are not responsible for enforcing compliance by third parties with this License.
An “entity transaction” is a transaction transferring control of an organization, or substantially all assets of one, or subdividing an organization, or merging organizations. If propagation of a covered work results from an entity transaction, each party to that transaction who receives a copy of the work also receives whatever licenses to the work the party’s predecessor in interest had or could give under the previous paragraph, plus a right to possession of the Corresponding Source of the work from the predecessor in interest, if the predecessor has it or can get it with reasonable efforts.
You may not impose any further restrictions on the exercise of the rights granted or affirmed under this License. For example, you may not impose a license fee, royalty, or other charge for exercise of rights granted under this License, and you may not initiate litigation (including a cross-claim or counterclaim in a lawsuit) alleging that any patent claim is infringed by making, using, selling, offering for sale, or importing the Program or any portion of it.
Patents.
A “contributor” is a copyright holder who authorizes use under this License of the Program or a work on which the Program is based. The work thus licensed is called the contributor’s “contributor version”.
A contributor’s “essential patent claims” are all patent claims owned or controlled by the contributor, whether already acquired or hereafter acquired, that would be infringed by some manner, permitted by this License, of making, using, or selling its contributor version, but do not include claims that would be infringed only as a consequence of further modification of the contributor version. For purposes of this definition, “control” includes the right to grant patent sublicenses in a manner consistent with the requirements of this License.
Each contributor grants you a non-exclusive, worldwide, royalty-free patent license under the contributor’s essential patent claims, to make, use, sell, offer for sale, import and otherwise run, modify and propagate the contents of its contributor version.
In the following three paragraphs, a “patent license” is any express agreement or commitment, however denominated, not to enforce a patent (such as an express permission to practice a patent or covenant not to sue for patent infringement). To “grant” such a patent license to a party means to make such an agreement or commitment not to enforce a patent against the party.
If you convey a covered work, knowingly relying on a patent license, and the Corresponding Source of the work is not available for anyone to copy, free of charge and under the terms of this License, through a publicly available network server or other readily accessible means, then you must either (1) cause the Corresponding Source to be so available, or (2) arrange to deprive yourself of the benefit of the patent license for this particular work, or (3) arrange, in a manner consistent with the requirements of this License, to extend the patent license to downstream recipients. “Knowingly relying” means you have actual knowledge that, but for the patent license, your conveying the covered work in a country, or your recipient’s use of the covered work in a country, would infringe one or more identifiable patents in that country that you have reason to believe are valid.
If, pursuant to or in connection with a single transaction or arrangement, you convey, or propagate by procuring conveyance of, a covered work, and grant a patent license to some of the parties receiving the covered work authorizing them to use, propagate, modify or convey a specific copy of the covered work, then the patent license you grant is automatically extended to all recipients of the covered work and works based on it.
A patent license is “discriminatory” if it does not include within the scope of its coverage, prohibits the exercise of, or is conditioned on the non-exercise of one or more of the rights that are specifically granted under this License. You may not convey a covered work if you are a party to an arrangement with a third party that is in the business of distributing software, under which you make payment to the third party based on the extent of your activity of conveying the work, and under which the third party grants, to any of the parties who would receive the covered work from you, a discriminatory patent license (a) in connection with copies of the covered work conveyed by you (or copies made from those copies), or (b) primarily for and in connection with specific products or compilations that contain the covered work, unless you entered into that arrangement, or that patent license was granted, prior to 28 March 2007.
Nothing in this License shall be construed as excluding or limiting any implied license or other defenses to infringement that may otherwise be available to you under applicable patent law.
No Surrender of Others’ Freedom.
If conditions are imposed on you (whether by court order, agreement or otherwise) that contradict the conditions of this License, they do not excuse you from the conditions of this License. If you cannot convey a covered work so as to satisfy simultaneously your obligations under this License and any other pertinent obligations, then as a consequence you may not convey it at all. For example, if you agree to terms that obligate you to collect a royalty for further conveying from those to whom you convey the Program, the only way you could satisfy both those terms and this License would be to refrain entirely from conveying the Program.
Use with the GNU Affero General Public License.
Notwithstanding any other provision of this License, you have permission to link or combine any covered work with a work licensed under version 3 of the GNU Affero General Public License into a single combined work, and to convey the resulting work. The terms of this License will continue to apply to the part which is the covered work, but the special requirements of the GNU Affero General Public License, section 13, concerning interaction through a network will apply to the combination as such.
Revised Versions of this License.
The Free Software Foundation may publish revised and/or new versions of the GNU General Public License from time to time. Such new versions will be similar in spirit to the present version, but may differ in detail to address new problems or concerns.
Each version is given a distinguishing version number. If the Program specifies that a certain numbered version of the GNU General Public License “or any later version” applies to it, you have the option of following the terms and conditions either of that numbered version or of any later version published by the Free Software Foundation. If the Program does not specify a version number of the GNU General Public License, you may choose any version ever published by the Free Software Foundation.
If the Program specifies that a proxy can decide which future versions of the GNU General Public License can be used, that proxy’s public statement of acceptance of a version permanently authorizes you to choose that version for the Program.
Later license versions may give you additional or different permissions. However, no additional obligations are imposed on any author or copyright holder as a result of your choosing to follow a later version.
Disclaimer of Warranty.
THERE IS NO WARRANTY FOR THE PROGRAM, TO THE EXTENT PERMITTED BY APPLICABLE LAW. EXCEPT WHEN OTHERWISE STATED IN WRITING THE COPYRIGHT HOLDERS AND/OR OTHER PARTIES PROVIDE THE PROGRAM “AS IS” WITHOUT WARRANTY OF ANY KIND, EITHER EXPRESSED OR IMPLIED, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE. THE ENTIRE RISK AS TO THE QUALITY AND PERFORMANCE OF THE PROGRAM IS WITH YOU. SHOULD THE PROGRAM PROVE DEFECTIVE, YOU ASSUME THE COST OF ALL NECESSARY SERVICING, REPAIR OR CORRECTION.
Limitation of Liability.
IN NO EVENT UNLESS REQUIRED BY APPLICABLE LAW OR AGREED TO IN WRITING WILL ANY COPYRIGHT HOLDER, OR ANY OTHER PARTY WHO MODIFIES AND/OR CONVEYS THE PROGRAM AS PERMITTED ABOVE, BE LIABLE TO YOU FOR DAMAGES, INCLUDING ANY GENERAL, SPECIAL, INCIDENTAL OR CONSEQUENTIAL DAMAGES ARISING OUT OF THE USE OR INABILITY TO USE THE PROGRAM (INCLUDING BUT NOT LIMITED TO LOSS OF DATA OR DATA BEING RENDERED INACCURATE OR LOSSES SUSTAINED BY YOU OR THIRD PARTIES OR A FAILURE OF THE PROGRAM TO OPERATE WITH ANY OTHER PROGRAMS), EVEN IF SUCH HOLDER OR OTHER PARTY HAS BEEN ADVISED OF THE POSSIBILITY OF SUCH DAMAGES.
Interpretation of Sections 15 and 16.
If the disclaimer of warranty and limitation of liability provided above cannot be given local legal effect according to their terms, reviewing courts shall apply local law that most closely approximates an absolute waiver of all civil liability in connection with the Program, unless a warranty or assumption of liability accompanies a copy of the Program in return for a fee.
END OF TERMS AND CONDITIONS
GNU LESSER GENERAL PUBLIC LICENSE
Version 3, 29 June 2007
Copyright (C) 2007 Free Software Foundation, Inc. <http://fsf.org/> Everyone is permitted to copy and distribute verbatim copies of this license document, but changing it is not allowed.
This version of the GNU Lesser General Public License incorporates the terms and conditions of version 3 of the GNU General Public License, supplemented by the additional permissions listed below.
Additional Definitions.
As used herein, "this License" refers to version 3 of the GNU Lesser General Public License, and the "GNU GPL" refers to version 3 of the GNU General Public License.
"The Library" refers to a covered work governed by this License, other than an Application or a Combined Work as defined below.
An "Application" is any work that makes use of an interface provided by the Library, but which is not otherwise based on the Library. Defining a subclass of a class defined by the Library is deemed a mode of using an interface provided by the Library.
A "Combined Work" is a work produced by combining or linking an Application with the Library. The particular version of the Library with which the Combined Work was made is also called the "Linked Version".
The "Minimal Corresponding Source" for a Combined Work means the Corresponding Source for the Combined Work, excluding any source code for portions of the Combined Work that, considered in isolation, are based on the Application, and not on the Linked Version.
The "Corresponding Application Code" for a Combined Work means the object code and/or source code for the Application, including any data and utility programs needed for reproducing the Combined Work from the Application, but excluding the System Libraries of the Combined Work.
Exception to Section 3 of the GNU GPL.
You may convey a covered work under sections 3 and 4 of this License without being bound by section 3 of the GNU GPL.
Conveying Modified Versions.
If you modify a copy of the Library, and, in your modifications, a facility refers to a function or data to be supplied by an Application that uses the facility (other than as an argument passed when the facility is invoked), then you may convey a copy of the modified version:
under this License, provided that you make a good faith effort to ensure that, in the event an Application does not supply the function or data, the facility still operates, and performs whatever part of its purpose remains meaningful, or
under the GNU GPL, with none of the additional permissions of this License applicable to that copy.
Object Code Incorporating Material from Library Header Files.
The object code form of an Application may incorporate material from a header file that is part of the Library. You may convey such object code under terms of your choice, provided that, if the incorporated material is not limited to numerical parameters, data structure layouts and accessors, or small macros, inline functions and templates (ten or fewer lines in length), you do both of the following:
Give prominent notice with each copy of the object code that the Library is used in it and that the Library and its use are covered by this License.
Accompany the object code with a copy of the GNU GPL and this license document.
Combined Works.
You may convey a Combined Work under terms of your choice that, taken together, effectively do not restrict modification of the portions of the Library contained in the Combined Work and reverse engineering for debugging such modifications, if you also do each of the following:
Give prominent notice with each copy of the Combined Work that the Library is used in it and that the Library and its use are covered by this License.
Accompany the Combined Work with a copy of the GNU GPL and this license document.
For a Combined Work that displays copyright notices during execution, include the copyright notice for the Library among these notices, as well as a reference directing the user to the copies of the GNU GPL and this license document.
Do one of the following:
Convey the Minimal Corresponding Source under the terms of this License, and the Corresponding Application Code in a form suitable for, and under terms that permit, the user to recombine or relink the Application with a modified version of the Linked Version to produce a modified Combined Work, in the manner specified by section 6 of the GNU GPL for conveying Corresponding Source.
Use a suitable shared library mechanism for linking with the Library. A suitable mechanism is one that (a) uses at run time a copy of the Library already present on the user’s computer system, and (b) will operate properly with a modified version of the Library that is interface-compatible with the Linked Version.
Provide Installation Information, but only if you would otherwise be required to provide such information under section 6 of the GNU GPL, and only to the extent that such information is necessary to install and execute a modified version of the Combined Work produced by recombining or relinking the Application with a modified version of the Linked Version. (If you use option 4d0, the Installation Information must accompany the Minimal Corresponding Source and Corresponding Application Code. If you use option 4d1, you must provide the Installation Information in the manner specified by section 6 of the GNU GPL for conveying Corresponding Source.)
Combined Libraries.
You may place library facilities that are a work based on the Library side by side in a single library together with other library facilities that are not Applications and are not covered by this License, and convey such a combined library under terms of your choice, if you do both of the following:
Accompany the combined library with a copy of the same work based on the Library, uncombined with any other library facilities, conveyed under the terms of this License.
Give prominent notice with the combined library that part of it is a work based on the Library, and explaining where to find the accompanying uncombined form of the same work.
Revised Versions of the GNU Lesser General Public License.
The Free Software Foundation may publish revised and/or new versions of the GNU Lesser General Public License from time to time. Such new versions will be similar in spirit to the present version, but may differ in detail to address new problems or concerns.
Each version is given a distinguishing version number. If the Library as you received it specifies that a certain numbered version of the GNU Lesser General Public License "or any later version" applies to it, you have the option of following the terms and conditions either of that published version or of any later version published by the Free Software Foundation. If the Library as you received it does not specify a version number of the GNU Lesser General Public License, you may choose any version of the GNU Lesser General Public License ever published by the Free Software Foundation.
If the Library as you received it specifies that a proxy can decide whether future versions of the GNU Lesser General Public License shall apply, that proxy’s public statement of acceptance of any version is permanent authorization for you to choose that version for the Library.
First issue of the library (2005/08/21). Creation of the manual.
The new version of the library is issued 2005/08/28. A few bugs have been corrected:
Correction for the reading of strain tensor, and curvature tensor in “op2” Nastran results file.
Correction of small bugs in the reading of element forces.
Addition of new capabilities:
Addition of the new functions “min”, “max” and “cmp” in the “Post” Module.
New methods have been added to the ResKeyList class.
The reading of strain/stress tensors, and of element forces is supported for additional element types.
The modifications of the manual correspond to the modifications of the library and of the examples:
Modifications corresponding to the reading of strain tensor from “op2” Nastran results file. Also, a few comments about the strain tensor have been added. Correspondingly, an example has been added (section IV.2.4.4).
Presentation of the new functions “min”, “max” and “cmp” in the “Post” module in section I.6.3.
Modification of the presentation of post-processing data definition for the calculation of margins of safety with the Cauchy stress tensor.
Modifications corresponding to the new methods introduced in the ResKeyList class (Chapter I.5).
The new version of the library is issued 2005/09/11.
The four elementary operators “+”, “-”, “*” and “/” allow now Float or Array left operands. The FeResPost library also modifies the corresponding classes.
Correction of a few small bugs.
The modifications of the manual correspond to the modifications of the library and of the examples:
The four elementary operators “+”, “-”, “*” and “/” allow now Float or Array left operands. The post-processing example as been modified accordingly.
The post-processing example has been modified in such a way that the methods defined in “Post” module are included in “Main” name space.
The new version of the library is issued 2005/11/06.
Correction of a bug in result extraction.
A new element coordinate system “elemIJK” is introduced.
Several modifications have been brought to the modifications of reference coordinate systems. (Possibility of projecting coordinate systems, for example).
The modifications of the manual correspond to some of the modifications of the library, and a little more:
Addition of Appendix X.A.4.6 devoted to the thoeretical background of transformation of coordinates.
Addition of an example illustrating the capabilities of coordinate system transformations (section IV.2.4.5).
The new version of the library is issued 2005/11/20.
The definition of local element (Nastran) coordinate systems has been modified.
The “CTETRA” element is now supported.
The reading of “op2” files is now more reliable. Previously tests were made with Nastran version 70.5 only. Now Nastran 2005 has been tested and a few bugs have been corrected.
Also, the reading functions check the “endiannes” of “op2” files and the performs the needed corrections when reading the content. This improves the portability of the result files from one platform to another.
The modifications of the manual correspond to some of the modifications of the library, and a little more:
Modification of the example illustrating the capabilities of coordinate system transformations (section IV.2.4.5). One more transformation is proposed. Moreover, one also gives an example with results on 3D elements.
The new version of the library is issued 2005/12/02.
Correction of few bugs.
Modification of the C++ programming of op2 reading. The reliability should be improved.
The third argument of function “modifyRefCoordSys” is now optional.
It is now possible to manipulate CoordSys objects and store them into a DataBase.
he modifications of the manual correspond to some of the modifications of the library, and a little more: an example, presented in section IV.2.4.5 illustrates the manipulation of coordinate systems.
The new version of the library is issued 2006/01/02.
Correction of few bugs.
More results types can be read from op2 files, and also results for other solution sequences can be read. (SOL 101, 103, 105 and 106 are now supported.)
Additional Nastran cards can be read from bdf or op2 file.
Some readings of entities in Nastran results or models can be desactivated.
A new function allows to calculate the total force and moment corresponding to a distribution of forces and moments. (see function “calcResultingFM” in section I.4.8.
Modification of “generateCoordResults” method in DataBase class. The method can now have three String arguments that correspond to the key to which the generated Result object is associated in the DataBase.
The modifications of the manual correspond to some of the modifications of the library, and a little more:
Modification of the example presented in section IV.2.4.1 to illustrate the modification of function “generateCoordResults” in DataBase class.
Addition of a new example in section IV.2.5.3 to illustrate the calculation of global force and moment transmitted by an interface.
The new version of the library is issued 2006/02/05.
Correction of few bugs.
Addition of method “writeBdfLines” to the “DataBase” class.
Addition of methods “renameResults” and “copyResults” to the “DataBase” class.
The modifications of the manual correspond to some of the modifications of the library.
The new version of the library is issued 2006/03/26.
Correction of few bugs.
The modifications of the manual correspond to some of the modifications of the library.
The new version of the library is issued 2006/05/26.
Modification of a few Nastran Result names.
Addition of a Samcef interface.
PCOMPG Nastran card is now supported.
New options for “deriveByRemapping” method in “Result” class. The new options are “mergeLayers” and “mergeLayersKeepId”.
Addition of methods “initWithOV2V1”, “initWithOV3V2” and “initWithOV1V3” to the “CoordSys” class.
Addition of method “setRefCoordSys” to the “Result” class.
Addition of method “extractResultOnLayers” to the “Result” class.
In nearly all functions dealing with layers, the layer may be identified either with String or integer objects. The correspondence between the two identification methods is summarized in Table I.4.4.
Addition of “extractLayers” and “extractGroup” methods to “Result” and “ResKeyList” classes.
The modifications of the manual correspond to some of the modifications of the library.
The new version of the library is issued 2006/07/02.
Reading of Dynam and Stabi Samcef Results.
Addition of “getSize” method to “Result” class.
Modification of “getResultCopy” method in “DataBase” class.
Modification of Result names to harmonize Samcef and Nastran Results access:
“Shell Forces” and “Shell Moments” for forces in 2D reduction elements.
“Beam Forces” and “Beam Moments” for forces in 1D reduction elements.
Beam Results in general.
Composite Results.
...
Some of the examples have been modified accordingly.
Correction of a few bugs.
The modifications of the manual correspond to some of the modifications of the library.
The new version of the library is issued 2006/07/23.
In the DataBase class, addition of several methods:
“readXdb” to import Result from a Nastran “xdb” file.
“removeAllResults” to clean the Results stored in a DataBase.
“eraseAllGroups” to erase all the Groups stored in a DataBase.
“getElementsAssociatedToMaterials”,
“getElementsAssociatedToProperties”,
“getElementsAssociatedToPlies”,
“getElementsAssociatedToLaminates”,
“getElementsAssociatedToAttr1s”,
“getElementsAssociatedToAttr2s”.
Also, two functions are now marked “to be deprecated soon”:
“getElementsAssociatedToMaterialId”,
“getElementsAssociatedToPropertyId”.
Addition of a few methods in the “Group” class:
“getNbrEntitiesByType”,
“getNbrEntities”.
Two methods added to “Post” module allow the activation and deactivation of Samcef Result codes:
“activateSamcefResCodes”,
“desactivateSamcefResCodes”.
A few modifications of Results corresponding to Bush and Gap elements.
Correction of a few bugs in the reading of Samcef composite Results.
The modifications of the manual correspond to some of the modifications of the library.
The new version of the library is issued 2006/08/20.
Correction to the beam element type forces and moments imported from Nastran Result files.
Improvement of the support for Samcef coordinate systems. However limitations for results given in element axes still exist!
Modification of the arguments of methods used to import Results. It is now possible to filter the Results being imported. (Modified methods are “readOp2”, “readXdb” and “readDesFac”.
The modifications of the manual correspond to some of the modifications of the library.
The new version of the library is issued 2006/11/05.
Redefinition of keys for force and stress Results on Nastran CBEAM and CSHEAR elements.
Redefinition of “getData” method and addition of “getStrData” method to the Result class.
Deletion of “getStrData” method from the Result class.
“getData” method from the Result class has now optional arguments that allow to tune the type of values returned in the Array. The values corresponding to the element, the node, the layer and the coordinate system may now be of integer or string type.
The "feresPost.so" library build by the Makefile is now output in the "FeResPost.so" file. Also, the classes "CoordSys", "ResKeyList", "DataBase", "Group", "Result" and the module "Post" are defined under the new module "FeResPost". The ruby programs using the previous versions of FeResPost must be modified. More precisely, the line
require "feresPost"
in the previous versions must be replaced by the two following lines:
require "FeResPost"
include FeResPost
and the rest of the program may be left unchanged.
Addition of the “lamCS” coordinate system identifier in the “result::values” class. Also, the use of “lamCS”, “matCS” and “plyCS” parameters in the “modifyRefCoordSys” method of “Result” class has been modified.
Correction of a bug in the reading of stresses on Nastran solid elements. (The reference coordinate system was wrong.) Similar corrections for the reading of layered results.
Correction of bugs when reading Samcef beam forces and moments.
Addition of several methods allowing the manipulation of flags influencing the behaviour of “readDesFac” method in “DataBase” class. This has been done to correct a bug in Samcef. Actually, only the “ANGULAR_STRAIN_BUG” flag can be set to correct errors in the shear components of strain tensor.
Addition of the “generateElemAxesResults” method to “DataBase” class.
Addition of the “sgn” derivation method for scalar Results.
Addition of the “deriveVectorToVector” method for vectorial Results.
The modifications of the manual correspond to some of the modifications of the library.
The new version of the library is issued 2006/12/10.
Addition of functions for the manipulation of abbreviations read from Samcef finite element models in the DataBase class. (Section I.1.7.)
Addition of a method allowing the renumbering of layers in a Result object. (Section I.4.6.3.)
Addition of a “writeGmsh” method to the DataBase class. (See section I.1.7.)
Addition of iterators to different classes (Group, Result, ResKeyList and DataBase classes).
A few modification of rules for coordinate system definitions and transformations on Results associated to elements with laminated properties. (See section I.4.6.7 and section X.B.5.)
The modifications of the manual correspond to some of the modifications of the library. Let us mention however:
Addition of an example illustrating the use of the new “writeGmsh” method of the DataBase class. This example is presented in section IV.2.5.4.
Modification of examples to illustrate the use of iterators. See for example, sections IV.2.2.2, IV.2.4.1, IV.2.4.4 and IV.2.4.5.
A few modification of rules for coordinate system definitions and transformations on Results associated to elements with laminated properties. (See section I.4.6.7 and section X.B.5.)
The new version of the library is issued 2006/12/18.
Correction of a bug in reading the OQG block of the Nastran op2 file.
A bug in the “writeGmsh” method of the “DataBase” class has been corrected.
Addition of “eachLcScId” iterator to DataBase class.
Modification of sub-case identifier of Results read in Samcef Results (asef module). One now names them with “Statics” instead of “Static SubCase”.
Addition of methods to the “Group” class: “clearEntitiesByType”, “importEntitiesByType”.
Suppression of the definition of assignment operators “+=”, “-=”, “*=”, “/=” in “Group”, “Result” and “ResKeyList” classes. However, these operators can still be used as ruby generates them automatically from the corresponding dyadic operators.
Addition of the “insert” method to the “ResKeyList” class that allows the user to fill its own ResKeyList objects.
Addition of the “insert”, “setTensorOrder” and “getTensorOrder”method to the “Result” class that allow the user to fill its own Result objects.
The modifications of the manual correspond to some of the modifications of the library. Let us mention however:
Modification of the example "EX04" presented in section IV.2.4.1.
The new version of the library is issued 2007/02/04.
When reading Nastran laminate ILSS failure indices, the "-1" values are no longer inserted in the Result.
Correction of a bug in the reading of stresses and strains from an xdb file.
Correction of a bug in reading Samcef results.
The modifications of the manual correspond to some of the modifications of the library. Let us mention however:
Modification of the post-processing program example. One now presents a simple modular example, and a more sophisticated object-oriented example.
The new version of the library is issued 2007/02/18.
Correction of a bug in the re-definition of “+”, “-” and “*” operators of the Array class.
Addition of sub-layer id field to the Result keys. Several classes and methods are affected by this modification:
Several methods of the “Result” class are modified: “getData”, “extractResultOnEntities”, “insert”, “each”, “each_key”.
One also added methods “extractResultOnSubLayers”, “extractSubLayers”.
Several methods of the ResKeyList class: “insert”, “each”. One also added “extractSubLayers” method.
When possible, one tried to modify the methods in such a way that previous versions of ruby programs using FeResPost were not to be deeply modified. Most modified methods do not require a corresponding modification of the ruby programs. However, for “getData” and “each” methods of Result class, more care is necessary. To ease the migration of post-processings, the previous version of “getData” still exists but has been renamed “oldGetData”.
It is now possible to read Samcef result codes 1???? and 2????. (Composite results on top and bottom surfaces of plies.) This is related to the addition of a sub-Layer ID in Result keys.
Addition of methods “activateSamcefSubLayerResCodes” and “desactivateSamcefSubLayerResCodes” to the “Post” module to desactivate the reading of sub-layer result codes from Samcef finite element Results.
Modifications in the importation of Nastran shell bending and curvature Results.
The modifications of the manual correspond to some of the modifications of the library.
The new version of the library is issued 2007/04/15.
Correction of a serious bug that affected all dyadic operations on Results. This bug resulted in segmentation faults when FeResPost was run on windows, in version 2.8.0.
Modification of the “writeGmsh” method in “DataBase” class. It is now possible to output Results at "ElemCenterPoints". Void Results are no longer output in the file.
Correction of a bug in the reading of Samcef banque file. No the reading should work for all types of line splitting.
Correction of a few other minor bugs.
Addition of CLA module for Classical Laminate Analysis calculations. The module is still under development.
The modifications of the manual correspond to some of the modifications of the library.
The new version of the library is issued 2007/05/01.
Correction of a few bugs in CLA module and its Classes:
Correction of a problem of material orientation in the calculation of laminate shear properties.
Correction of the “each_ply” iterator in Laminate Class.
Addition of an example illustrating the out-of-plane shear calculations with CLA modules.
It is now possible to define temperature loadings with different upper skin and lower skin temperatures.
Addition of moisture contribution to the loading. (Based on the same principles as the temperature loading.)
The modifications of the manual correspond to some of the modifications of the library (among other things the modifications of the thermo-elastic and hygrometric aspects of the CLA calculations). The theoretical Chapter has been deeply transformed.
The new version of the library is issued 2007/05/06.
Correction of a bug in some string manipulation instructions. (The problem appeared only for some computer architecture.)
Modification of the methods used to manipulation temperature and moisture contributions in Load class of CLA module.
Better support of anisotropic materials.
Better distinction of material types when mechanical, CTE and CME characteristics are defined.
The modifications of the manual correspond to some of the modifications of the library.
The new version of the library is issued 2007/05/13.
Correction of a bug is Result methods "extractOnLayers" and “extractOnSubLayers”.
Correction of a bug in “getResultCopy” method of DataBase class. (The bug occurred when the one extracted result for a selection of entities AND on a list of layers or sub-layers.)
Addition of the reading of composite strength ratios in Nastran “op2” files.
Improvement of the reading of ESAComp edf files: now laminates with repetition of layers or symmetry are supported.
The modifications of the manual correspond to some of the modifications of the library.
The new version of the library is issued 2007/05/20.
The “Cla::DataBase” class has been renamed “CLA::CompDb”. (This to avoid confusions between the “FeResPost::DataBase” and “FeResPost::CLA::DataBase” classes.)
Addition of CLA methods to the “DataBase” class. The methods are devoted to the manipulation of “CompDb” class that stores materials and laminates corresponding to finite element model stored in the DataBase object.
Correction of a bug in the reading of ESAComp "edf" files.
Correction of a bug in the definition of anisotropic materials in CLA module.
The modifications of the manual correspond to some of the modifications of the library.
The new version of the library is issued 2007/07/01.
Suppression of the concept of “active” CLA::CompDb object. The corresponding methods of the CLA::CompDb class have been cancelled.
It is now possible to insert Result objects into CLA::Load objects (“Shell Forces”, “Shell Moments”, “Shell Strains”, “Shell Curvatures”, “Shell Temperatures”, “Shell Moistures”)..
In relation to this modification, the methods “setT” and “setH” of the Load object have one additional parameter specifying the type of component to consider for laminate load response. Also the type of mechanical components “femFM” and “femSC” have been introduced. Also, eighteen methods for finite element Results insertions have been introduced in “Load” class (section II.5.6).
Addition of two iterators in the “DataBase” class: “each_nodeOfElement” and “each_cornerNodeOfElement”. An example illustrating the use of these iterators has been added.
Addition of the “Mid” sub-layer ID. Also the correspondence between sub-layer names and sub-layer IDs has been changed.
Addition of the method “calcFiniteElementResponse” to the “Laminate” class. The same method has been added to “CompDb” class too.
The modifications of the manual correspond to some of the modifications of the library. Moreover:
In the “testSat” example, the bottom panel is modeled with surface elements and laminates properties corresponding to a sandwich panel with laminated skins.
Examples “EX15” and “EX16” have been added to the “RUBY” examples. (Example “EX15” illustrates the production of composites Results from other finite element Results.)
The new version of the library is issued 2007/07/11.
Correction of a bug in the reading of continuation cards in Nastran Bulk Data Files.
Support for “include” statements in Nastran Bulk Data Files. Now the Bulk Data Files can be split in several files.
Support for “input” statements in Samcef banque files. Here again, this allows to split the model in several files.
The modifications of the manual correspond to some of the modifications of the library. Moreover:
Restructuration of the presentation of the ‘testSat” model, with one version with xdb outputs, and one version with op2 outputs.
The examples have been updated to take the modifications of “readBdf” in “DataBase” class into account. (“include” statements.
The new version of the library is issued 2007/07/29.
Correction of a bug in the reading 1D element forces from Nastran “op2” result files.
Correction of a bug in the reading of SPOINT elements from Nastran Bulk Data File.
Addition of the method “getdXdbLcInfos” to the “DataBase” class.
Addition of the methods “setFormat” and “getFormat” to the “Result” class.
The previously deprecated method “oldGetData” has been completely deleted.
It is now possible to read Complex Results from a Nastran xdb file. Nastran SOL107, SOL108 and SOL111 are supported.
Methods devoted to the manipulation of Complex Results have been defined in the “Result” class. (See section I.4.9.)
Correction of several bugs in reading Nastran Bulk Data Files. Among other things, the reading of free format cards has been improved.
Results from CELASi elements can now be read from an xdb Nastran Result file.
The modifications of the manual correspond to some of the modifications of the library. Moreover:
Addition of an example illustrating the manipulation of Complex Results.
The discussion of examples has been modified according to these different modifications.
The new version of the library is issued 2007/08/05.
Correction of a bug in the reading of binary xdb files.
Correction of a bug in the reading of continuation fields when bulk data files are read.
When Nastran Results are read, different load case names are attributed to Results with no load case titles.
The “Complex” class is no longer automatically required when FeresPost is loaded.
Modification of classes and methods specific to the composite calculations:
The classes “CLA::CompDb”, “CLA::Laminate”, “CLA::Material” and “CLA::Load” have been renamed “ClaDb”, “ClaLam”, “ClaMat” and “ClaLoad” respectively.
These new classes are defined directly in “FeResPost” module. The “FeResPost::CLA” module has been erased.
Several “Composite” Methods of the “DataBase” class have been renamed: “buildClaDb”, “getClaDbCopy”, “setClaDb” and “clearClaDb”.
The modifications of the manual correspond to some of the modifications of the library.
The new version of the library is issued 2007/08/26.
“DataBase” class is now virtual and two specialized classes have defined: “NastranDb” and “SamcefDb” classes. The “DataBase” class no longer can be instantiated. This is a modification of the extension that mirrors deep restructuration of the C++ programming of FeResPost.
In “DataBase” class, methods “buildClaDb”, “getClaDbCopy”, “setClaDb” and “clearClaDb” have been suppressed. Instead, a method “getClaDb” has been inserted.
The DataBase methods “getElementsAssociatedToMaterialId” and “getElementsAssociatedToPropertyId” have been deprecated.
Addition of method “getResultSize” to the generic DataBase class.
Correction of a bug in the reading of Des and Fac Samcef Result files.
Reading of new Samcef Codes: 1413, 3413, *423.
Addition of a seventh optional parameter to the “readDesFac” method in SamcefDb class.
Four singleton methods for activating and deactivating Samcef Result Codes have been displaced from “Post” module to “SamcefDb” class.
Similarly, five singleton methods of the “Post” module have been displaced in “NastranDb” class as singleton methods.
Modification of the Makefiles organization for compiling the code. The “build.bat” to be used for compiling in Windows environment is suppressed. Now the compilation is to be done with “make” command on windows too. (Installation on MSYS on windows might be necessary.)
The modifications of the manual correspond to some of the modifications of the library.
The new version of the library is issued 2007/09/02.
In “readBdf” method of “NastranDb” class, a few bugs have been corrected. (Among other things problems around void lines, or splitting of bulk Data Files.)
Correction of a bug in the reading of strain tensor per plies from an xdb file.
In CLA classes and methods, the “Equivalent Strain Tensor” is renamed “Mechanical Strain Tensor”. Correspondingly, the method “getPliesEquivStrains” is renamed “getPliesMechanicalStrains”.
Addition of “calcFiniteElementCriteria” to DataBase and ClaLam classes.
The modifications of the manual correspond to some of the modifications of the library.
The new version of the library is issued 2007/09/30.
Modification of ClaLam methods devoted to the manipulation of allowables.
Modification of ClaMat methods devoted to the manipulation of allowables, moduli, CTEs and CMEs.
Addition to the ClaMat class of methods allowing to recover characteristics in specified direction. Some of the already existing methods have been renamed.
Possibility to retrieve absolute and relative ply temperature and moisture when laminate load response is calculated.
Modification of the calculation of in plies with CLA module.
Modification of “max” and “min” methods in “Post” module.
Addition of “insertRklVals” method to the “Result” class.
Addition of a sixth parameter in “writeGmsh” method of DataBase class. The logical parameter is used to trigger binary or ASCII output.
Modification of the identification of sub-cases when Samcef Results are read from “des” and “fac” files. The new denomination is now closer to the Nastran one. Also the integer and real values associated to Results have been modified.
Addition several of Mecano Thermal elements support in Samcef preferences.
Several Mecano Thermal Results can now be read.
A few bugs have been corrected.
The modifications of the manual correspond to some of the modifications of the library. A few examples illustrating the modification of CLA classes have been added. Several correction in CLA theory and classes descriptions.
The new version of the library is issued 2007/10/07.
Addition of methods “getGroupAllElements”, “getGroupAllNodes”, “getGroupAllRbes”, ‘getGroupAllCoordSys”, “getGroupAllFEM” to the DataBase class.
Addition of method “renumberSubLayers” to the Result class.
Modification of the reading for Shell Laminate Stresses from Nastran Results. Now the inter-laminar stresses are better taken into account.
Addition of method “calcFemLamProperties” to DataBase class (I.1.5).
Correction of a few bugs.
The modifications of the manual correspond to some of the modifications of the library. Moreover:
The examples in “TESTSAT/RUBY/EX15” has been modified. A modification of coordinate system of the shell Results is done to obtain them in laminate axes.
The new version of the library is issued 2007/11/04.
Addition of methods “readGroupsFromPatranSession” and “readGroupsFromSamcefDat”to the “Post” module.
Correction of a few minor bugs.
Addition of composite failure criteria in CLA classes, or renaming of some of the existing criteria.
Some failure criteria imported from Samcef or Nastran finite element Results have been renamed.
Critical ply Results are no longer produced when Nastran layered failure indices are read from a Nastran op2 file.
Corrections brought to the calculation of Tsai-Wu criterion.
Addition of several derivation methods for the “deriveDyadic” method of Result class. Corresponding methods have been added to the “Post” Module.
Addition of the “writeGmshMesh” method to the generic “DataBase” Class. Modification of the corresponding example in section IV.2.5.4.
Finalization of the separation of solvers (Nastran and Samcef).
The modifications of the manual correspond to some of the modifications of the library. Moreover:
The manual is completely restructured in such a way that the preferences for the different supported solvers are discussed in a separate Part of the manual.
Addition of the example “TESTSAT/RUBY/EX02/writeGroupEntities.rb” that illustrates the reading of Groups into a Hash object.
Addition of examples illustrating the calculation of composite failure indices from shell forces and moments. The examples are defined for static load cases as well as dynamic ones.
The new version of the library is issued 2008/01/01.
Correction of a bug in the reading of ILSS from ESAComp EDF files.
Addition of new capabilities to the method “modifyRefCoordSys” in “Result” Class.
The modifications of the manual correspond to some of the modifications of the library. Moreover:
Addition of an example illustrating the “Beam Forces” and “Beam Moments” recovered from Nastran CBAR element Results.
Addition of an example illustrating the new capabilities of “modifyRefCoordSys” method in DataBase Class.
New explanation for the coordinate systems in NastranDb and SamcefDb Classes.
More information about the peculiarities of “writeGmsh” methods in NastranDb and SamcefDb Classes.
Minor modification of example “EX01/readBdf”. An error message is issued if the second “readBdf” fails.
The new version of the library is issued 2008/01/13.
Addition of methods for the activation/deactivation of reading of composite layered Results. These methods are defined in generic DataBase class (section I.1.3.2).
Correspondingly the two methods “activateSamcefSubLayerResCodes” and “desactivateSamcefSubLayerResCodes” previously defined in SamcefDb class have been erased.
Correction of a small bug in the reading of ILS failure indices from Nastran op2 Result files.
The modifications of the manual correspond to some of the modifications of the library. Moreover:
Modification of the example in section IV.2.4.1 to illustrate the deactivation of composite element layered results reading.
The new version of the library is issued 2008/01/20.
Correction of a bug in the reading of Nastran PBEAM properties.
Reading of the nodal temperature results from Nastran “op2” and “xdb” result files.
The name of sub-cases no longer include the units of time or frequencies (when applicable). For example “Mode 1 (f = 2.2526 Hz)” becomes “Mode 1 (f = 2.2526)” and “Step 12 (t = 8.6591 s)” becomes “Step 12 (t = 8.6591)”.
Correction of a small bug in the modification of coordinate systems for Nastran Results.
The modifications of the manual correspond to some of the modifications of the library. Moreover:
Correction of an error in the description of methods in Group class “clearAllEntitiesByType” method).
Small modification of the example devoted to the manipulation of complex Results in sectionIV.2.4.6.
The new version of the library is issued 2008/01/27.
Removing a few “write” statements that has been added for debugging of the PBEAM property reading.
“readBdf” method of NastranDb class has now up to five arguments. The additional argument corresponds to symbols that can be substituted in the file names in include statements.
The modifications of the manual correspond to some of the modifications of the library. Moreover:
The example illustrating the reading of Nastran Bulk Data Files has been modified to illustrate the use of symbols in include statements and the related modifications in NastranDb “readBdf” method.
The new version of the library is issued 2008/02/03.
Addition of a parameter to “readOp2” method of “NastranDb” class to allow the reading of op2 Result files for post-processors other than Patran.
Reading of the “BOPHIG” and "BOUGV1" result tables from op2 files.
Reading of Nastran element energies from op2 files as well as xdb files.
he modifications of the manual correspond to some of the modifications of the library.
The new version of the library is issued 2008/02/10.
Correction of a bug in the extraction of CoordSys objects from Nastran or Samcef DataBases.
Correction of several bugs in the manipulation of user-defined CoordSys objects.
Modification of the method “initWith3Points” defined in “CoordSys” class. A DataBase object must be added to the list of arguments.
A few modification of reading of des and fac files into “SamcefDb” DataBases.
he modifications of the manual correspond to some of the modifications of the library. Moreover:
The post-processing examples have been modified. Addition of criteria to the PostConnect class and correction of one bug in the calculation of the norm of direction defining the axis of a connection.
The new version of the library is issued 2008/02/24.
Correction of a bug in “extractResultOnLayers” method in Result class.
A few other minor modifications.
The modifications of the manual correspond to some of the modifications of the library.
The new version of the library is issued 2008/03/30.
Modification of CLA classes for the calculation of thermal and moisture diffusion quantities.
Addition of methods “removeLayers” and “removeSubLayers” to the “Result” class.
Addition of methods “removeLayers” and “removeSubLayers” to the “ResKeyList” class.
Reading of “conductive Heat Flux” and “Temperature Gradient” Results from Nastran op2 and xdb Result files.
Correction of a bug in the reading of Samcef Results.
A few other minor modifications.
The modifications of the manual correspond to some of the modifications of the library. Moreover:
Addition of an example illustrating the calculation of Laminate thermal properties.
Correction of a few minor errors in the manual.
The new version of the library is issued 2008/04/20.
Modification in the reading of beam bending moments from Samcef Results.
The modifications of the manual correspond to some of the modifications of the library. Moreover:
Addition of more explanation about sign conventions for beam force and moments tensors.
Addition of lists of methods defined in the different classes of FeResPost.
Correction of a few minor errors in the manual.
The new version of the library is issued 2008/04/27.
Correction of a bug int the reading and manipulation of Nastran “PCOMP” property cards with “SYM” option.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected.
The new version of the library is issued 2008/05/25.
Addition of method “generateShellOffsetsResult” to the SamcefDb class.
Addition of method “extractResultOnResultKeys” to the Result class.
Modification of method “getResultcopy” in generic DataBase class.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected.
The new version of the library is issued 2008/06/08.
Correction of a bug in the reading of Grid Point Forces from Nastran xdb file. Class NastranDb is modified.
Addition of the methods “writeGroupsToPatranSession” in generic DataBase class and Post module.
The lists of entities to be stored in Groups can now be defined in ranges with steps: for example “ ... firstId:lastId:step ...”.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected. Moreover:
Addition of an example illustrating the manipulation of entities stored in a Group and the use of method “Post::writeGroupsToPatranSession” (section IV.2.2.3).
Modification of Appendix X describing the installation and compilation of FeResPost.
Modification of the introduction of the manual.
The new version of the library is issued 2008/06/15.
Correction of a few minor bugs related to error messages.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected.
The new version of the library is issued 2008/07/06.
Addition of “getData” and “getSize” methods to “ResKeyList” class.
Addition of attributes setters and getters to several classes.
Modification in the, reading of BDF files. Now the reading should be more reliable for “special cases”, even though the reverse is also possible. (If you have problems, do not hesitate to send examples of data leading to bugs.)
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected.
The new version of the library is issued 2008/09/07.
All the attributes have been renamed. Their name starts now with an uppercase letter.
The two methods “get_abbd” and “get_g” have been renamed “get_abbd_complMat” and “get_g_complMat”.
Addition of methods “eraseMaterial”, “getMaterialsNbr”,“eraseLaminate”, “getLaminatesNbr”,“eraseLoad” and “getLoadsNbr” to the “ClaDb” class.
Correction of several bugs in the reading of Nastran Bdf and Samcef Dat files.
FeResPost is no longer open source.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected.
The new version of the library is issued 2008/10/06.
The FeResPost library is now distributed as a COM component (on windows).
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected.
The new version of the library is issued 2008/10/19.
Correction of a bug in Result filtering when Nastran xdb stress Results are read.
Correction of a bug in COM conversion of boolean arguments.
Correction of two bugs in methods of ClaMat class returning CME properties.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected. Description of the “CLA in excel” example has been improved and the example modified.
The new version of the library is issued 2008/10/26.
Correction of a bug in the division of tensorial results by real values.
Addition of the exponentiation “**” operator to the “Result” class.
Addition of methods “getPliesStrainsWrtLamAxes”, “getPliesStressesWrtLamAxes” and and “getPliesMechanicalStrainsWrtLamAxes” to ClaLam class (Section II.4.7.3).
Addition of “clearData” method to Result class.
Modification of “insertRklVals” method in Result class. Now, the first argument can also be a Result object.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected.
The new version of the library is issued 2008/11/16.
The “each” iterator of ResKeyList class in ruby extension is renamed “each_key”.
Modification of the arguments for singleton method “writeNastran” of NastranDb class in ruby extension. The method has been renamed “writeNastranCard”. One also defines the new method “writeNastranCards”.
The “writeBdfLines” of NastranDb class is ruby extension has also been modified.
Correction of bugs in some iterators on FE entities ID of the NastranDb and SamcefDb classes. (When specified, the lower ID was not well taken into account.)
In “SamcefDb” class, method “each_samcefMaterialId” has been renamed “each_samcefPlyId”. This new name corresponds to what the method does.
In COM component, the classes “Group”, “CoordSys” and “ResKeyList” are more or less terminated. The “NastranDb” and “SamcefDb” classes are in progress.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected. New examples illustrating the manipulation of Groups and the use of iterators with the COM component are given.
The new version of the library is issued 2008/11/23.
Correction of a bug in SamcefDb class of COM component: the two “readSamcefDat” and “readDesFac” methods were permuted.
Addition of several methods in generic DataBase class.
Addition of several methods in “Application” class.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected.
The new version of the library is issued 2008/12/07.
Addition of methods “getNeutralLines” and “initWithNeutralLines” in the four CLA classes.
Addition of several methods in Result class.
Addition of several methods in “Application” class.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected. The “CLA in excel” example has been modified to illustrate the use of new methods.
The new version of the library is issued 2008/12/14.
Correction of a bug in the reading of Samcef BUSH element results.
Correction of a bug in method “writeGroupsToPatranSession”. (Void Groups resulted in erroneous session lines.)
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected.
The new version of the library is issued 2009/01/04.
Addition of methods “opAdd”, “opSub”, “opMul” and “opdiv” in the “Post” Module.
The modification of “Float” and “Array” classes is done in a separate ruby source file and no-longer in the compiled shared library.
Correction of a bug in methods returning laminate stresses and strain (“ClaLam” class of FeResPost ruby extension). The structure of Results was not as stated in the manual. The examples have been updated according to the modification.
The different classes in the COM component are now completely programmed, and several bugs have been fixed.
Addition of different methods for XDB files content investigation to the “NastranDb” class.
A small correction in the calculation of Tsai-Hill reserve factors: when the failure index is negative, the RF is 1e+20.
Addition of several methods to FE DataBase classes to investigate the content of the model (number of elements, nodes, groups,...).
A small modification in the parameters of the “getResultCopy” in generic DataBase class.
The “none” keyword for merging method of “deriveByRemapping” in Result class is replaced by “NONE”.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected. Moreover:
Several examples using the COM component have been added. These examples have also been used to fix several bugs.
The new version of the library is issued 2009/03/01.
Correction of a bug in the reading of XDB Results. No Results were previously read for SOL101 analyses when the loading was purely thermo-elastic.
Addition of units management to the different CLA classes.
The CFAST element is now supported.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected. Moreover:
Correction of the “sol106.bdf” data file.
Addition of examples illustrating the manipulation of CLA classes units systems.
The new version of the library is issued 2009/03/08.
Correction of a bug in the construction of a Composite DataBase from Nastran or Samcef Databases: now the density of materials is correctly initialized.
Addition of several mass units in CLA ("t", "dat" and "kbm").
Correction of a bug in method “matchWithDbEntities” of Group COM class. (There was one “Release” too much.)
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected.
The new version of the library is issued 2009/03/29.
“Bizarre” points are skipped with a warning message when “OUG” or “OQG” blocs are read by a “readOp2” statement.
Modifications that should increase the robustness of reading of groups from Patran session files.
Addition of a “SwapEndiannes” optional argument to methods devoted to XDB files access. This argument allows to force the swap of endiannes when reading the binary file.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected.
The new version of the library is issued 2009/05/24.
Addition of new layers corresponding to groups of layers in Results keys. (For extraction operations.) Similarly, one adds one new sub-layer for extractions.
A few modification of interpretation of element properties when elements are read into a SamcefDb object. The modified method for reading Samcef banque files should be more reliable.
Correction of bugs in the conversion of Boolean variables in COM component.
Addition of methods for XDB random access in NastranDb class.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected.
Moreover, excel examples using COM component have been improved. In particular, one added an example illustrating random access to XDB results. Also small ruby examples illustrating the use of random access have been added.
The new version of the library is issued 2009/06/07.
Addition of a memory buffer to XDB attachments.
Addition of method “writeMsgOutputLine” to “Post” Module.
Huge memory leak problems in the COM component have been solved.
Correction of several problems related to String conversions in COM component.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected.
The new version of the library is issued 2009/06/21.
Correction of several bugs in the filtering on elements/nodes when Results are read on a given Group from a Nastran XDB file.
A few bug corrections in the conversions of arguments in COM component.
The reading of Nastran composite layered stress Results has been modified. Values are no longer produced in top and bottom skins of each ply.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected.
Moreover, a post-processing project in excel using COM component is presented. (See Chapter VII.4.)
The new version of the library is issued 2009/07/12.
Correction of a bug in the random access to XDB files. (When nodal values were read on a Group, the first node was skipped.)
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected.
The excel post-processing project has been improved.
The new version of the library is issued 2009/08/02.
Correction of several bugs in the conversion of matrices in COM component.
Correction of a bug in the conversion of Arrays of Boolean in COM component.
Correction of a bug in the calculation of laminate finite element load response. (The bug resulted in several criteria not being calculated.)
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected.
The excel post-processing project has been improved and several corrections have been done in the manual.
Also the presentation of the examples has been improved. One separates the examples with FeResPost ruby extension on one side, and with FeResPost component on the other side. The excel examples are presented in separate chapters.
The new version of the library is issued 2009/08/23.
Random access to Samcef “des” and “fac” Result files.
Addition of one “UNDEF” layer for Result keys.
Most methods of “NastranDb” class devoted to the manipulation of XDB attachments have been renamed. (The “Xdb” in method name has been removed.)
Addition of method “getAttachmentNbrSubCases” to “NastranDb” class.
Correction of a bug in the conversion of “SamcefDb” arguments in COM component.
Correction of several bugs related to the modification of coordinate systems for beam Results.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected.
Moreover:
Correction of Samcef Contact Result names in the manual.
Suppression of the example illustrating sequential access to Nastran XDB Results with excel.
Addition of an example illustrating random access to Samcef DES/FAC Results with excel.
Modification of the excel post-processing example to allow the post-processing of Samcef Results as well as Nastran Results.
The new version of the library is issued 2009/11/08.
Correction of a bug in the writing of Nastran cards in wide format.
Correction of a bug in the reading of Groups from Patran session files. (Now several “ga_group_entity_add” statements can be interpreted for a single Group, or a Group can be build by reading several session files.)
Correction of a bug in method “deriveByRemapping” method of Result class. The “MergeLayersKeepId” option did not keep the layer as it should.
Correction of a bug in the writing of GMSH meshes for Nastran models.
The new version of the library is issued 2009/12/13.
Correction of several bugs in the CLA calculations (ClaLam class).
Correction of a bug in the creation of COM component. (The creation of component was not possible with several languages.)
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected.
The new version of the library is issued 2010/01/03.
Modification of method “getAttachmentNbrSubCases” in “NastranDb” class.
Addition/modification of several DES/FAC “attachment” methods to the “SamcefDb” class. (The purpose of these modifications is to defined the same methods in “NastranDb” and “SamcefDb” class.
Addition of several checks when results are read from Nastran XDB files (insertion of pairs key-values for composite results in particular).
Addition of methods “isThermalLoadingDefined”, “isMoistureLoadingDefined” and “isMechanicalLoadingDefined” to the “ClaLam” class.
Correction of a bug in the management of units for Classical Laminate Analysis.
Modification of the management of storage buffers for methods and classes providing random access to binary Result files. (Presently, Nastran XDB files and Samcef DES/FAC files.) After the modification the, management of buffers is common to the different result attachments. The maximum capacity for storage buffers is managed by singleton methods “setStorageBufferMaxCapacity” and “getStorageBufferMaxCapacity” of the generic “DataBase” Class. The corresponding methods of “NastranDb” and “SamcefDb” classes have been deleted.
Correction of a bug in the reading of Nastran SOL107 Results from XDB files.
Correction of a bug in the simplification of include paths when Nastran BDF files are read with “readBdf” method of “NastranDb” class. The same correction has been done for the reading of Samcef Bacon files with “readSamcefDat” method of “SamcefDb” class.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected.
Moreover:
In examples “RUBY/EX13”, modification of the source file “extendedCLA.rb” to illustrate the use of new “ClaLam” class methods. The manual is modified accordingly.
The new version of the library is issued 2010/01/24.
Correction of a bug in the storage buffer for Result reading. (Previously, the actual size of buffer was 16 times the size specified by the call of “setStorageBufferMaxCapacity”.)
Correction of a bug in the reading of Samcef contact result codes 1305, 1306 and 1307 from FAC result files.
Correction of a bug in the reading of abbreviations from Samcef "dat" files.
he modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected. Moreover:
In examples “RUBY/EX13”, modification of the source file “extendedCLA.rb” to illustrate the use of new “ClaLam” class methods. The manual is modified accordingly.
The new version of the library is issued 2010/01/31.
Correction of small bugs in the random access to Nastran XDB result files.
Improvement of the reading of ESAComp files. Now version 4 files are supported as well as those of version 3.4.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected. Moreover:
Addition of installation instructions to the distributed ruby extensions and COM components.
Modification and documentation of the COM excel examples.
The new version of the library is issued 2010/02/07.
Correction of a bug in the extraction of Result eigen-values. Previously, the extraction algorithm sometimes failed when two eigen-values were very close to each other.
Correction of a bug in the reading of Nastran BDF files. The rules for including sub-files have changed.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected. Moreover:
More explanation is given about the rules applied by FeResPost to include sub-files when Nastran BDF files are imported into a DataBase.
Some tidying up of the manual (among other things in the list of versions and changes).
Addition of the example “RUBY/EX01/readBdf_V3.rb” to test new versions of file includes statement in BDF read with “readBdf” of “NastranDb” class.
The new version of the library is issued 2010/02/21.
Correction of a bug in the reading of result code 221 (reaction forces and moments) from Samcef Mecano des/fac files.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected. Moreover:
Additional information on the Hash object returned by “getAttachmentResults” and “getAttachmentResultsCombili” in NastranDb and SamcefDb classes.
New example “RUBY/EX19/attachedXdbExtract.rb” illustrating the extraction of Results from XDB attachments.
The new version of the library is issued 2010/04/11.
Correction of several bugs here and there. Most of these bugs are related to segmentation faults that appear when using the Microsoft Visual C++ compiler.
Correction of several bugs in the reading of Nastran CBEAM element forces, stresses and strains from XDB result files.
Correction of a bug in Nastran XDB files reading. Now, results produced with SORT2 Nastran output can be read as well as those produced with SORT1 option.
Addition of flag “DES_FAC_DEBUG” to SamcefDb class to allow the debugging of Des/Fac Result files access.
Modification in the reading of Samcef Des files: lines containing NULL characters are now accepted by FeResPost. (Note that we consider this as a bug in Samcef, as it is very nasty to add NULL characters in a file that is supposed to be formatted.)
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected. Moreover:
Additional information on the reading of composite stresses from Nastran op2 or xdb result files. (In particular about the out-of-plane shear stress components.)
The example described in section VII.2 (Classical Laminate Analysis with Excel) is slightly modified: for spreadsheets calculating laminate load response in which loading is directly defined in the spreadsheet, loading units are now the same as the laminate ones. (Loading is no longer defined with default units.)
In “calcLamLoadResponse” module, methods “calcLamOopShearForces” and “calcLamOopShearStrains” have been added. Spreadhseets “LamLoadResponse_A” and “LamLoadResponse_B” have been modified to use the new methods.
The new version of the library is issued 2010/05/02.
Correction of several bugs in COM conversions, and iterators.
Addition of a second version of Yamada-Sun criterion (more adapted to the justification of fabrics).
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected. Moreover:
The Laminate Analysis example with Excel has been updated. (Several bugs were fixed in thee excel VBA.)
The new version of the library is issued 2010/08/18.
FeResPost is now also distributed as a .NET assembly.
In CLA classes, the “Id” attribute is no longer accessible by methods “setId” and “getId”. Instead, the corresponding attributes (ruby) or properties (COM and .NET) have to be used.
In all classes, the “Name” attribute is no longer accessible by methods “setName” and “getName”. Instead, the corresponding attributes (ruby) or properties (COM and .NET) have to be used.
In class ClaMat, the material type can no longer be accessed by “setType”, “getType” and “getTypeName” methods. Instead, the corresponding attributes (ruby) or properties (COM and .NET) have to be used.
In “Result” class, several “set” or “get” methods have become attributes. These methods correspond to “Name”, “TensorOrder”, “Format” and “Size” attributes. (Note that the “size” attribute or property has been renamed “Size”.)
Similarly, The “Size” and “Name” attributes of “ResKeyList” class have been modified. Note that the “size” attribute or property has been renamed “Size”.)
in “ClaLam” class, the methods returning load results by ply have been modified: the returned values have a different format.
In “ClaLam” class of COM component, the methods “getMaxDerived”, “getMinDerived”, “getMaxFailureIndices”, “getMinFailureIndices”, “getMaxReserveFactors” and “getMinReserveFactors” returns 2 dimensional Arrays of sizes N*3.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected. Moreover:
The new version of the library is issued 2010/10/17.
Methods “setVerbosityLevel” and “getVerbosityLevel” have been added to “Post” Module.
Methods “convertIdfierToString” and “convertStringToIdfier” have been added to “Post” Module.
Correction of several small bugs in the .NET assembly, and in the reading of Nastran BDF cards in free format.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected. Moreover:
Correction in the “PostProject.xls” COM example: there was a problem in the extraction of connection loads.
The COM examples with Excel have been modified to allow debugging by setting the value of a “verbosityLevel” variable.
...
The new version of the library is issued 2010/11/01.
Correction in method “convertStringToIdfier” of “Post” Module.
Correction of method “getOOPSStiffness” in “ClaMat” Class.
Correction of a small bug in the reading of RBE3 MPC elements from Nastran BDF files.
Several memory leaks have been quenched.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected. Moreover:
Minor corrections in the manual and in the examples.
...
The new version of the library is issued 2010/11/14.
Several minor bugs have been fixed (memory leaks).
A few modifications in the construction of Groups to avoid a too large use of RAM.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected. Moreover:
Several corrections in the “PostProject.xls” example to reduce the use of computer memory.
...
The new version of the library is issued 2011/02/20.
Correction of a several memory leaks that occurred when exceptions were thrown. (Cleaning of temporary variables when exceptions were thrown.)
Addition of methods in “Group” and “Result” classes that allow the conversions between these objects and SQL BLOBs.
In .NET assembly, the assignment operators (operator=) of the FeResPost classes, have been removed.
In .NET assembly, definition of “finalizer” methods in FeResPost classes. (Huge memory leaks!)
in COM component: correction of an error in vector<result*> conversion.
...
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected. Moreover:
Addition of examples illustrating the manipulation of FeResPost BLOBs with SQLite.
FeResPost is again distributed under the terms of the general public license.
The new version of the library is issued 2011/03/13.
Correction of a bug in blob conversion of Results. (Conversion failed when “void” Results were considered.)
A few modifications in the output of Results in GMSH files. Now the Results should be output without problem even when some of the keys do not match finite element entities (nodes or elements) defined database.
The modifications of the manual correspond to some of the modifications of the library and a few errors in the manual have been corrected. Moreover:
Modification of the post-processing with excel project. It is now possible to save an SQLite3 database that can be used a posteriori to build envelopes of Results to be saved in GMSH files.
The new version of the library is issued 2011/04/25.
Correction of a bug in “addResult” of generic DataBase class. (A huge memory leak.)
Correction of a bug in the random access to XDB results. (Previously latest key-value pairs in data blocks were sometimes “forgotten”.)
Correction of bug in “attachDesFac” method of “SamcefDb” class. (In some cases, the method failed and FeResPost crashed.)
Modification of the manual and examples:
Modification of the post-processing with excel project. The method “getCurrentDb” of “DbAndLoadCases” Module has been modified to ensure that the last DataBase is returned.
Also in post-processing with excel example, the Module “ResultsGmsh” has been modified in such a way that the post-processing also works when SQLite is not available, or installed in a different location.
Addition of a spreadsheet for manipulation of Groups in examples “PostXdbRandom.xls” and “PostDesFacRandom” examples.
The new version of the library is issued 2011/06/05.
Correction of a bug in XDB files random access. Now the access to files alarger than 1 Tb should work. (Previously the limit was approximately 2 Gb.)
Correction of a bug in Nastran FAC files random access. Now the access to files alarger than 1 Tb should work. (Previously the limit was approximately 2 Gb.)
The “activate” and “desactivate” methods have been renamed “enable” and “disable”.
Modification of the manual and examples:
Examples have been modified to correspond to the new “enable” and “disable” methods
The new version of the library is issued 2011/07/24.
The COM component is now also distributed as an out-of-proc (EXE) server.
The new version of the library is issued 2011/09/18.
Correction of a bug in the reading of CSHEAR element stresses from op2 files. (The “elemId” field of result keys was not initialized.)
Reading of CONROD and CSHEAR results from xdb files.
COM component is provided with a Proxy/stub dll.
The new version of the library is issued 2011/09/25.
Attribution of a default load case name when Results are read from Nastran OP2 or XDB files and no SUBTITLE has been defined in the corresponding Nastran SUBCASE definition.
Special care has been taken to correctly identify the version of .NET assembly.
Modification of the manual and examples:
Update of the manual according to the modifications of the library.
Update of information on the component registration.
The new version of the library is issued 2011/11/06.
Addition of the “FromTo” parameters “MergeSubLayers” and “MergeSubLayersKeepId” for the method “deriveByRemapping” of “Result” class.
Modification of “getData” methods of “Result” and “ResKeyList” classes in such a way that they return coherent default “string” or “int” values. (Coherence between the two classes, but also between the ruby extension, COM component and .NET assembly.)
Addition of the methods “getElementType”, “getElementTypeName”, “getElementDim”, “getElementNbrNodes”, “getElementNbrCornerNodes” to the generic DataBase class.
Addition of the method “getElementPropertyId” to the NastranDb class.
Distribution of a “vbaruby” bridge for the embedding of ruby in MS-Office programs, and the dispatch of VBA calls to ruby interpreter. (See X.F.7.)
A few improvements in the “writeBdfLines” method of “NastranDb” class.
Modification of the manual and examples:
Modification of the example “RUBY/EX16/elemConnectivity.rb”.
Elimination of “ResultsEnveloper” module from “COMEX/EX10/PostProject.xls” example.
Addition of an example illustrating the use of vbaruby bridge to call ruby post-processing programs from excel. (See Appendix X.F.7.)
The new version of the library is issued 2012/01/02.
Addition of methods allowing to access the characteristics of nodes in NastranDb and SamcefDb classes. (Access to coordinates, ACID or RCID.)
Addition of methods “checkAbbreviationExists”, “checkCoordSysExists”, “checkElementExists”, “checkNodeExists” and “checkRbeExists” in the generic “DataBase” class.
In the “CoordSys” class, addition of methods allowing the transformation of point coordinates, or vectors and tensors components.
Modification of the manual and examples:
Description of the new methods have been added in the user manual.
Addition of an example illustrating the transformation of point coordinates and vector or tensor components in the “CoordSys” class. (See section IV.2.4.5.)
The new version of the library is issued 2012/02/26.
A few very minor modifications of the source code.
For the ruby extensions and COM component, the ruby and COM “wrappers” are now separated from the FeResPost C++ “core” library.
Modification of the manual and examples:
The information about installation, configuration and compilation of FeResPost and associated libraries has been gathered in Appendix X. A careful reading of this Appendix is recommended because the modifications of binaries organization influences the way they must be installed.
The new version of the library is issued 2012/06/10.
A few very minor modifications of the source code.
Correction of a bug in the .NET iterators. (The first element of each collection was missing.)
Four attributes (properties) added to the “Group” class: “NbrElement”, “NbrNodes”, “NbrMpcs” and “NbrCoordsys”.
Modification of the manual and examples:
Modification of examples to illustrate the use of the new Group attributes.
Modification of the “VBARUBY” bridge and corresponding example. The new version should work better with the 1.9.* versions of ruby.
The new version of the library is issued 2012/06/17.
Correction of a bug in “getNodeRcId”, “getNodeAcId” and “getNodeCoords” methods of the “NastranDb” class. (The return values always corresponded to the first call to the method.)
The new version of the library is issued 2012/08/19.
Addition of several error messages, and more tests for error detection.
Correction of a few minor bugs.
Addition of methods “getElementNodes” and “getElementCornerNodes” to the generic “DataBase” class.
The new ruby extensions and COM component are now statically linked to the FeResPost object. The use of a shared library containing all FeResPost C++ classes is no longer necessary. Static linking is recommended for your own programs/extensions.
The new version of the library is issued 2012/11/04.
Correction of a few bugs.
Better separation of the different Nastran and Samcef specific classes from the “common” classes. (This is internal stuff related to the programming of coordSys classes, but should be of no consequence for the library users.)
The COM and .NET iterators have also been re-organized. (Here again, the modifications should be of no consequence for the library user.)
The new version of the library is issued 2013/01/27.
Correction of a bug in the reading of Nastran BDF files.
Correction of a bug in the reading of Nastran XDB files.
Addition of four methods for the reading of Nastran SOL200 results (experimental). The four methods are “getAttachmentDesVarHistory”, “getAttachmentConstrDefinitions”, “getAttachmentConstrHistory” and “getAttachmentObjectiveHistory”.
The new version of the library is issued 2013/02/17.
Small correction in Samcef and Nastran dataBase headers that prevented the compilation with GCC versions 4.6.*.
Correction of a bug in the reading of the history of constraints from Nastran SOL200 XDB results.
Addition of method “getAttachmentDesRespHistory” to NastranDb class.
Correction of a bug in the reading of Nastran BDF files, or Samcef DAT files. (too long lines stalled the program before correction.)
The new version of the library is issued 2013/04/14.
Correction of a bug in the calculation of mechanical strain tensor in laminates: previously (until version 4.1.6), the “total” or “actual” strain tensor were returned at bottom layer of the plies.
Distinction between strain tensor criteria calculated with mechanical and total strain tensor components respectively. The default strain criteria are now using the mechanical strain tensor. (Previously, only the total strain tensor was used. It is still possible to use it with the “Total” version of each strain criterion.)
Correction of many typographical errors in FeResPost User Manual.
The new version of the library is issued 2013/05/19.
Correction of bugs in the reading of Nastran PBEAM properties.
Some cleaning of the code.
A few modifications in user manual.
The new version of the library is issued 2013/07/07.
Correction of a bug in the reading of the CBAR element stresses and strains.
Correction of several bugs in the reading of Nastran BDF files (reading of CORD1R, CORD1C, CORD1S, RBE1 and PSHELL cards).
The new version of the library is issued 2013/08/04.
Correction of a bug in the reading of the PBEAM properties from BDF files.
Correction of a bug in the PCOMP properties with symmetric laminates.
Addition of the support for 64bits XDB result files.
The “PostPproject.xls” example has been optimized. (Post-processing with COM component and excel.)
A few modifications in User Manual.
The new version of the library is issued 2013/08/18.
Correction of a several bugs in the XDB access:
Problems related to the identification of load cases.
Problems related to the reading of very large XDB files (size>2Gb).
The new version of the library is issued 2013/09/22.
Addition of four singleton methods to the Result class for the conversion of layer and sub-layer string and integer IDs.
Correction of a bug in the reading of BDF files: some real values were not recognized.
Modification of the acceptable COM arguments for conversion to “vector3”. Now, one accepts two-dimensional arrays 1*3 or 3*1. (Previously, only one-dimensional arrays were accepted.)
Modification of the “PostXdbRandom.xls” and “PostDesFacRandom.xls” workbooks that now allow to extract Results expressed in projected coordinate systems, and/or to select the layers for which values are extracted.
The new version of the library is issued 2013/11/11.
For Nastran Results, one now makes the difference between (linear) Stress and Strain tensors, and the “Nonlinear” corresponding results. Nonlinear stress and strain Results are read for CHEXA, CPENTA, CTETRA, CQUAD4 and CTRIA3 elements.
Modification of the Results for Nastran CGAP elements.
Correction of a bug in the reading of design variables history for Nastran SOL 200 output.
Correction of a bug in the “writeGmsh” method in generic “DataBase” class:
Previously only one value was printed per element/node was printed when several were present in the output Results. This may have been a problem when multi-layered Results were output.
Now an error message is issued when this kind of problem is detected and FeResPost throws an exception. (This error message is influenced by verbosity level.)
The responsibility of producing mono-layered Results for GMSH output is the user’s responsibility.
Correction of a bug in the reading of surface element forces, strain or stresses from XDB files. (Results at element corners were sometimes wrong.)
Correction of a bug in the reading of shell element complex strain and curvature Results from Nastran XDB files. (Generally, the curvatures were not correctly interpreted.)
CQUADR and CTRIAR element Results can now be read from XDB files.
Correction of a bug in “scanBdf” method of NastranDb class: comments in BDF lines are better taken into account.
Addition of “MergeAll” accepted value for “FromTo” parameter of “deriveByRemapping” in Result class.
Singleton methods “enableNasResElems” and “disableNasResElems” have been renamed “enableOp2ResElems” and “disableOp2ResElems” respectively.
Addition of singleton methods “enableXdbTables” and “disableXdbTables” to the NastranDb class to allow a better filtering of XDB tables reading.
Addition of the three “getBulkCardsEnableInfos”, “getOp2ResElemsEnableInfos” and “getXdbTablesEnableInfos” singleton methods in NastranDb class.
The description of Results read from Nastran OP2 and XDB result files has been updated (in particular, the reading of non-linear analysis Results from SOL 106, 129 and 400 analyses.
“printXdbDictionnary” method has been added to NastranDb class.
Modification of nil argument conversions in Strings or Arrays, Hashes: the conversion results in a void String, or Array or Hash.
The new version of the library is issued 2014/01/04:
The reading of Nastran 32 bits and 64 bits OP2 files is now possible.
The examples are also modified:
The post-processing project in excel has been updated. A button has been added to the “LcSelector” spreadsheet to help the debugging of data.
The new version of the library is issued 2014/02/02:
Correction of several memory segmentation bugs related to the replacement of several “strncpy” by “memcpy” in issue 4.2.4 of the library.
Addition of “initToZero” method to the “Result” class.
The new version of the library is issued 2014/08/24:
Correction of two bugs in the “checkGroupExists” and “checkAbbreviationExists” methods of the generic DataBase class in ruby extension.
For the reading of Nastran BDF files, the “rfinclude” and “rfalter” include statements are now taken into account. Note however than in FeResPost, these statements are considered to be strictly equivalent to the usual “include” statement.
Correction of a bug in the identification of included files in the “include” statements of “readBdf” method.
Modification of “min” and “max” derivations in “deriveDyadic” method of the Result class. Now, the dyadic derivation can be done for vectorial or tensorial Results. (See section I.4.5.)
Correction of a bug in the modification of coordinate systems wrt which the components of tensors or vectors are expressed. (The THETA parameter used in the definition of material orientation was not always taken into account.)
Addition of BBBT accessor to XDB files. Previously, only the HK access was supported. Note However that the reading of Grid Point Forces fails and throws an exception if several sub-cases are defined in a load case (SOL103, sol105, SOL106...).
The new version of the library is issued 2015/01/01:
Correction of a bug in the reading of Nastran BDF files: the “include” statements on several lines before “BEGIN BULK” statement are now processed correctly (hopefully without bug).
Correction of several bugs in the conversion of COM Arrays. (Segmentation faults possible when exceptions were thrown.)
Addition of “writeNastranCardToVectStr” method to “NastranDb” class.
Addition of methods “getMpcNodes”, “getMpcDependentNodes” and “getMpcIndependentNodes” to “NastranDb” class.
Correction of a bug in “writeGmsh” method of “DataBase” class. Problems occurred when void Strings were associated to Result, Mesh or Skeleton outputs.
Correction of a small bug in “scanBdf” method of “NastranDb” class. (Management of the include directories.)
Correction of the Python examples with COM component.
A few corrections in the User Manual.
The new version of the library is issued 2015/01/18:
Correction of a major bug in the reading of Nastran BDF files: the “include” statements should work better now. (The “corrections” in version 4.2.7 were actually catastrophic.)
A few corrections in the User Manual.
The new version of the library is issued 2015/04/06:
Correction of a bug in the Nastran CoordSys class. (The building of CORD1R, CORD1C or CORD1S wrt 0 failed when the nodes defining the object were defined wrt 0.)
Correction of a bug in the reading of stresses or strains from XDB files at corners of solid elements.
Addition of method “fillcard” to the NastranDb class. (See section III.1.1.5.)
A few corrections in the User Manual.
The new version of the library is issued 2015/04/19:
Correction of a bug in the conversion of Nastran MAT8 material to ClaMat object. (The “STRN” parameter was not taken into account.)
the “LaminateAnalysis.xls” example using COM component has been slightly improved.
The major modification in this issue of FeResPost is that it is now distributed under the Lesser General Public License. Practically, this means that it is now allowed to distribute proprietary applications linked with the library. (See Appendix X.H.4 for more information.)
The new version of the library is issued 2015/08/26:
Addition of an example with ruby extension illustrating the access to optimization results (RUBY/EX21). The manual is modified accordingly (section IV.2.7).
In “NastranDb” class, the “writeNastranCard”, “writeNastranCards” and “writeNastranCardToVectStr” have been modified. The “cardName” String argument has become optional. The User Manual and corresponding examples have been adapted.
Addition of several “raw XDB access” methods to the “NastranDb” class. The methods are described in section III.1.1.10 and illustrated by examples in section IV.2.8.
The new version of the library is issued 2015/11/22:
Correction in the reading of shell element stresses at mid-thickness. The stresses are associated to “NONE” layer, and no longer to “Z0”. (This has been done to ensure coherence with other shell results reading. User manual is updated accordingly.
The reading of Nastran XDB result files produced with option “DBCFACT=4” has been nearly completely re-programmed. It seems that all the results that can be read with “DBCFACT=0” can also be read with “DBCFACT=4”.
Correction of a major bug in the “modifyRefCoordSys” method of “Result” class. (The modifications from spherical, or to spherical coordinate systems were completely erroneous before version 4.3.2.)
The new version of the library is issued 2016/01/01:
Correction of a few minor bugs:
FIXED: in GMSH output, no output was produced when one or several Result keys failed.
FIXED: program crashed when operands were of wrong type.
FIXED: wrong error message in Result extract operation.
Small optimization of XDB files indexed with hash keys.
Addition of a “BulkOnly” Logical parameter to the “readBdf” method in “NastranDb” class.
Addition of method “writeNastranCardsToVectStr” to the “NastranDb” class.
Addition of methods “insertCard” and “insertCards” to the “NastranDb” class. (These methods allow to modify the model defined in the “NastranDb” object.)
Addition of “atan2” dyadic function in the “Post” Module.
The “Post.pow” method now also allows a Float as first argument.
The “Post.vectProduct” method allows vectors (Arrays of three Float) as first or second argument. Note also that the “vectProduct” operation in ”deriveDyadic” method of “Result” class has also been modified and also allows an Array of three real values as second argument.
Addition of the “setComponent” method to the ‘Result” class.
Some of the “xdb” methods in NastranDb class have been transformed in ruby singleton method, or in .NET static methods. (It does not change the bahaviour of COM component.)
Addition of the special node IDs “CbarGrdA” et “CbarGrdB” to allow the reading of moments and stresses in CBAR elements that are not defined in the dataBase. (See Table III.1.6.)
A few corrections in the examples, and in the user manual.
The new version of the library is issued 2016/03/06:
Correction of a bug in “getNodeCoords” in “NastranDb” class. Now the coordinates wrt coordinate system 0 can be obtained.
Correction of a bug in “Post.cmp” method.
Correction of a bug in the writing of GMSH “mesh” files.
Addition of support for the unisgned int and unsigned long int in NastranDb raw accessor to XDB tables (“u” and “U” conversions).
Some modifications on the manual and the distributed binaries:
Modifications that correspond to the modifications of FeResPost libraries.
The procedure for building the binaries from sources have been cleaned somewhat, and should be easier to adapt and use for anyone.
The number of available binaries has been increased. (More versions of Ruby are now supported, in 32bits or 64bits. The .NET CLR versions 2 and 4 are supported.)
The new version of the library is issued 2016/06/05:
Correction of bugs in the XDB raw iterator. (The unsigned int conversion was missing in COM component and .NET assembly.)
Correction of a bug in the “writeGroupsToPatranSessionFile” in the COM Application object. (Sometimes, the “Groups” argument was not well converted.)
Correction of a bug in the calculation of CLA finite element load response. (The thermo-elastic and hygro-elastic contributions were not correct.)
Relaxation for the syntactic rules in BDF files read with “readBdf” method of NastranDb class. Integers are now accepted as real values when no ambiguity is possible.
A few corrections in the manuals.
Binaries for the versions 2.3.* of ruby are also distributed.
Addition of examples showing how the temperature distributions applied for thermo-elastic loading of Nastran models can be retrieved and used for the calculation of laminate load response. (See sections IV.2.8.5 and VII.4.4.3.)
The new version of the library is issued 2016/08/16:
Correction of several methods with variable number of arguments:
Method “setComponent” in “Result” class.
Methods “getAttachmentNbrSubCases” and “getNodeCoords” in “NastranDb” class.
Methods “getAttachmentNbrSubCases”, “generateShellOffsetsResult” and “getNodeCoords” in “SamcefDb” class.
Correction of a bug in the “insert” method of “Result” class. (The “NONE” element ID of key was not accepted.)
Correction of arguments in methods “removeLayers” and “removeSubLayers” of “Result” class in .NET assembly.
Correction of arguments in methods “removeLayers”, “removeSubLayers” and “extractResultOnEntities” of “Result” class in COM component.
In COM component: correction of a bug in the “writeBdfLines” singleton method of “NastranDb” class.
Correction of a bug in the extraction of corner nodes in Nastran scalar elements “CMASS1”, “CMASS2”, “CDAMP1”, “CDAMP2”, “CELAS1” and “CELAS2”. (This bug affected several other methods as “writeGmshMesh”.
The limit on lines length when Nastran BDF or Samcef DAT files are read has been elmininated.
Correction of a bug in the “Result” class modification of reference coordinate systems. (Previously, transformation was erroneous when curvilinear coordinate systems were used in the orientation of material properties in shell elements.)
Introduction of the “Ilss_b” version of the composite inter-laminar shear stress failure criterion in CLA classes. (See section II.1.10.27.)
Addition of method “containsEntity” to the “Group” class.
In the description of generic “DataBase” class in User Manual, methods “getNbrCoordSys”, “getNbrElements”, “getNbrNodes”, “getNbrAbbreviations” and‘getNbrGroups” are now presented as they are: as attributes “NbrCoordSys”, “NbrElements”, “NbrNodes”, “NbrAbbreviations” and “NbrGroups”.
A few “cosmetic improvement of the manuals (addition of internal links).
COM component installation program “registrySetup.exe” has been renamed “modifyRegister.exe”. (This has been done to “dodge” Windows 10 User Access Control that does not like executables containing the word “setup”.)
Elimination of dirty spurious “QueryInterface” error messages from the COM component.
The new version of the library is issued 2016/11/01:
Correction of a bug in “setComponent” methods of “Result” class when two parameters are passed to the method. (One bug for all extensions, and another bug for the COM component only.)
Correction of a bug in the XDB reading/attachment, when anonymous load cases are present in the XDB file (SUBCASES with no SUBTITLE).
In Ruby extension, correction of a bug in “modifyRefCoordSys” method of “Result” class. (The method returned “Self” instead of nil.)
Correction of a bug in the XDB access with BBBT index (option DBCFACT=4). (It seems that no index is produced when the table is stored in a single page.)
Improvement of the test for big/little endianness of XDB files. A warning message is issued in case of “doubt”. The manual is modified accordingly (section III.1.1.9.10).
Correction of a bug in the extraction of nodes in Nastran scalar elements “CMASS1”, “CMASS2”, “CDAMP1”, “CDAMP2”, “CELAS1” and “CELAS2”. (This bug affected several other methods as “writeGmsh”.
Addition of method “calcRandomResponse” in the “Post” module.
Addition of method “deriveScalPerComponent” in the “Result” class.
Addition of “VonMises2D” derivation method for the “deriveTensorToOneScal” method.
Addition of method “deriveVectorToTensor” to the “Result” class.
A sixth optional argument has been added to the “calcResultingFM” class method in “Result” class. This argument allows to provide the list of coordinates used for the calculation of global moment. This can be handy when the forces are not associated to nodes. (Element forces extracted from CBUSH elements, for example.)
The new version of the library is issued 2017/01/02:
Correction of a bug in “deriveVectorToTensor” method of “Result” class.
Correction of a small error in User Manual (description of the “calcRandomResponse” method in “Post” module.)
Addition of information in Appendix X devoted on installation instructions. (Discussion of execution environment, of installations of both 32 bits and 64 bits versions of the COM component, on GNU C++ re-distributable libraries.)
Correction of a bug in the Result modification of reference coordinate system when one of the system is curvilinear and the result values are associated to element center. (Error was related to the fact that the location of element center is obtained by averaging the nodal coordinates in a curvilinear CS instead of a cartesian one.) Errors with previous versions were very small in most cases.
Correction of a bug in method “calcResultingFM” of the Result class. In some cases, results were erroneous when curvilinear coordinate systems were used in the calculations.
Improvement of the “modifyRefCoordSys” in Result class. New version should be faster when several modifications are done on results related to the same FEM entities. In some cases, the time saving can be very significant.
Improvement of the different operators in the “Result” class. Among other things, a better support for calculations with complex numbers is provided.
The “Post.vectProduct” method also supports calculations with complex numbers.
The new version of the library is issued 2017/03/19:
Correction of a bug in the reading of Nastran “PBEAML” property cards. (Method “readBdf”in “NastranDb” class.)
Correction of a bug in the reading of Nastran BDF files. Comment lines inside Nastran Cards were causing problems. (Method “readBdf” in “NastranDb” class.)
Minimum support for the “CORD3G” Nastran card.
Correction of a bug in a few dyadic operators in Result class. (Bad initialization of cId in some cases.)
Modification of the “operator” methods in ruby “Post” module (COM component “Application” class). Now, the new methods cover the corresponding operators and dyadic functions in “Result”, “Group” and “ResKeyList” classes. (See section I.6.4 for more information)
Improvement of “generateCoordResults” method in DataBase class. Now, error messages are printed when missing nodes are detected, but no exception is thrown.
A few optimizations of the code. In particular, the composite Result calculations have been significantly accelerated. (See section II.1.9 for a detailed explanation.)
Method “reInitAllPliesAccelMatrices” added to the “ClaLam” and “ClaDb” classes. (This modification is related to the acceleration of composite calculations.)
Correction of a few bugs in the conversion of array arguments of COM component.
Addition of a ninth parameter to “calcFiniteElementResponse” and “calcFiniteElementResponse” methods.
The new version of the library is issued 2017/05/28:
Modification of “calcFiniteElementResponse” method. ILSS criteria are always calculated at bottom ply if requested, even if no output request at bottom sub-layers.
Introduction of the concept of “Strength Ratio” in classical laminate analysis (sections II.1.10 and II.4.7.5).
A few corrections in “calcRandomResponse” method of “Post” Module. The User Manual has been corrected too.
Addition of method “calcPredefinedCriterion” in “Post” Module in order to accelerate computations (optimization of post-processing operations).
The new version of the library is issued 2017/08/27:
Correction of a bug in the Result class “multi iterator”. This correction should fix the problem in “SGI_SR” predefined criterion.
In COM component: correction of a bug in the conversion of complex vector to variant.
Correction for the reading from XDB files of complex stresses in CBEAM elements (MP format).
In “DataBase” class of the component, the “NbrAbbreviations”, “NbrGroups”, “NbrCoordSys”, “NbrElements”, “NbrNodes”“get*” methods are replaced by property “getters”.
Several bug fixes.
The most significant innovation is that FeResPost is also distributed as a Python library.
The new version of the library is issued 2017/10/22:
Modification of the “WriteGmsh” method in “DataBase” class. A check of the Result values is done and infinite of NaN values are substituted with MAXFLOAT and MINFLOAT respectively.
Correction of string conversion in PYTHON version > 3. C/C++ strings are now converted to Unicode strings, and no longer to bytes.
The problems related to the different operators in the Python extension “Result” class have been fixed. It is now possible to use the “+”, “*”, “*”, “/” and “**” operators. The corresponding “opAdd”, “opSub”, “opMul”, “opDiv”, “opPow” methods have been removed. (This means you will have to modify your Python scripts if you have used these methods.)
Correction of the “extractLayers” and “extractSubLayers” methods in “Result” class. The methods return the “NONE” layers or cub-layers, and corrections are done in COM component and .NET assembly.
The new version of the library is issued 2018/01/01:
In ruby extension, addition of a “coerce” method in the “Result” class for the management of operators with “Result” object as second argument. (See section I.7.) The standard classes are no longer modified by “modifStdClasses.rb”.
Addition of “opPow” method in “Post” Module.
In the .NET assembly, for compatibility with other FeResPost libraries, one has defined the “opAdd”, “opSub”, “opMul”, “opDiv” and “opPow” methods in the “Post” Module.
Correction of a bug in the reading of Results from XDB files produced with option “DBCFACT=4” (BBBT accessor). The reading failed when the table fitted a single page (output of a small amount of data).
Correction of a bug in method “deriveTensorToThreeScals” of “Result” class.
Addition of method “eigenQR” to “Result” class.
In Windows binaries, python extensions are now compiled with GNU compiler.
The new version of the library is issued 2018/04/29:
Correction of a bug in the “insertLaminate” of the “ClaDb” class. The method no longer returns an exception when laminate properties calculation fails.
Correction of a bug in the reading of text files on UNIX and LINUX systems. The DOS “end-of-line characters” were not well supported. This bug fix concerns the reading of Nastran BDF files, Samcef DAT files, composite databases from EDF or NDF files and groups from Patran session files.
correction of a bug in the generation of GMSH “skeletons”. (Segmentation fault occured if one node used in element definition was missing.)
Modification of “LaminateAnalysis.xls” example. Now the material and laminate thermal and moisture properties are also calculated in the corresponding spreadsheets. Also, one improved the calculation of minimum or maximum composite criteria.
A few corrections in the User Manual. For example, some remarks have been added to the description of CBUSH element forces and moments read from Nastran results.
Addition of a few checks on “NULL” arguments for “claDb” and "ClaLoad" arguments.
Correction of a major bug in Python complement. (The bug prevented numerical operations of Result class objects with other type’s arguments.) This bug concerns the version 2.* of Python.
Several other bugs have been fixed in the Python complement.
Addition of an object oriented post-processing in the Python examples (section V.1.4).
Several errors have been correction in the Python examples.
The new version of the library is issued 2018/08/05:
Correction of a bug in reading of CBUSH element complex stresses from XDB file.
Addition of method “importAttachmentResults” in “NastranDb” class.
Renaming the complex nodal Results read from XDB. The (RI) or (MP) is now at the end of Result name, and no longer at the beginning. Examples and manual are updated accordingly.
Correction of a bug in the “deriveScalToScal” method in “Result” class. (The method was completely wrong when applied to complex results.)
Correction of a bug in “deriveVectorToScal” method in “Result” class. The format of Result object is always set to Real for “abs” and “sq” derivation, even if the argument is a Complex vectorial Result.
Correction of a bug in the “max” and “min” dyadic derivation methods of “Result” class. Results were not correction when keys belonged to only one of the Results, and when the Results were tensorial or vectorial.
Modification of the “compare” method behaviour for “deriveDyadic” in “Result” class. Now the method can also be used with vectorial or tensorial Results. Then, the comparison is done on a component-per-component basis.
Modification of the “writeGmsh” method in generic “DataBase” class. The method now also accepts the “Elements” as output location for the Results.
Correction of a bug in the “writeGmsh” method in generic “DataBase” class. The function should no longer crash when one attempts to output empty or nil Results in GMSH files.
Correction of a bug in the reading of composite stresses/strains from Nastran XDB and OP2 files. When inter-laminar results are read, a rotation of the shear components is now done to obtain results in ply axes. (Nastran produces inter-laminar shear results in laminate axes.)
Correction of a bug in the reading of Nastran XDB result files produced with option “DBCFACT=4”. Results directly written in the indexation data pages, isntead of in separate data blocks are now read correctly. This is the case, for example, for the spring scalar forces. (We suspects Nastran does not create separate data pages when corresponding data are small and can be stored in a number of words <=2.)
A few other improvements of the XDB access with option “DBCFACT=4”.
The laminate interlaminar shear criteria are no longer calculated at bottom layer of laminates bottom ply.
Addition of a test on the number of components of values inserted into “Result” objects.
Correction of a bug in the reading of nonlinear stresses and strains from Nastran XDB files.
Addition of several methods in the “Result” class: “cloneNoValues”, “insertResultValues” and “removeKeysAndValues”.
Production of compiled extensions for ruby version 2.5.* and Python version 3.7.*. (However, I have problems to run the FeResPost extension with versions 2.4.* and 2.5.* of ruby on windows OS.)
A few corrections in User Manual.
The new version of the library is issued 2019/02/10:
Correction at several places in the sources codes of errors related to the check of “nbrValues” for insertion in Results.
Correction of two bugs for the conversion of blob objects:
In ruby extension, on makes a check on nil values.
In Python library, one corrects a bug in the method of “Post” module that converts blobs.
COM component and ruby or python extensions are now statically linked to GNU compiler libraries “libm.a” and “libstdc++.a”. This should facilitate the installation of FeResPost as the GNU C++ redistributable libraries are then no longer needed to use FeResPost.
Correction of two bugs in the reading of XDB results produced with option DBCFACT=4 for Nastran SOL 106.
Correction of bug in the calculation of reaction forces and moments. They are now calculated as the summation of SPC forces or moments. The Reaction forces are now also available when results are read from XDB files.
Correction of several bugs in the reading of complex results in magnitude-phase format from XDB files. The errors concern the reading of “Beam Forces”, “Shell Moments”, “Shell Curvatures’, “Strain Tensor” and “Stress Tensor”. (The errors were related to some components wrong sign corrections of the phase part of results.)
Correction of the reading of strain tensor shear components on CSHEAR, CROD, CONROD, CTUBE and CBEND elements. (Division by two in order to have “real” tensor component instead of angular shear strains.)
Correction of the reading of strains, stresses, forces and moments from XDB on CTRIA6 and CQUAD8 elements.
Void Results read from XDB files are now erased from the list of Results read from the file.
Addition of support for the reading of Nastran Results from HDF files. Programming of this part is under way and support is only partial:
em The HDF support is not available yet in .NET assembly!
No support for the reading of optimization results.
No support for the reading of thermal results.
Only partial support for the reading of nonlinear analyses results. (Result tables specific to nonlinear analyses are not read.)
...
We are working on these limitations and expect progress soon. See sections III.1.1.11 and I.6.11 for more information.
The new version of the library is issued 2019/03/02:
Reading of Nastran HDF5 Result files is now possible in .NET assemblies CLR version 4. It does not compile with CLR version 2 however.
Minor bug fixes (wrong error messages).
Extension of support for Nastran CWELD element.
Addition of method “getHdfAttachmentLcInfos” to NastranDb class.
The new version of the library is issued 2019/07/16:
Correction of method “getHdfAttachmentResults” in NastranDb class.
The reading of Grid Point Forces, MPC Forces and Moments has been improved to cover the cases when Nastran option “RIGID=LAGR” has been used. The correction has been done for the reading of results from OP2, XDB and HDF5 files.
Detection of MPC and Element ID clashes when Nastran FEM is read.
Correction of a bug in the division operator of Result class. (There was a problem when one Result was Real and the other is Complex.)
A few modification of the “deriveByRemapping” method of “Result” class. The modification consists mainly in the fact that one now distinguishes the “CornerNodes” (Result keys associated to elements and nodes at corner of elements) and the “ElemsAndNodes” (Result keys associated to elements and nodes of elements but not necessarily at their corners).
The registration of out-of-proc COM component is no longer discussed in current manual, and the corresponding information fields no longer appear in COM registration program. (See section X.A.4.5.)
Several methods of the “Result” class have been modified in such a way that the method returns the modified object. The modified methods are “clearData”, “insert”, “insertRklVals”, “insertResultValues”, “setComponent”, “removeKeysAndValues”, “setRefCoordSys”, “renumberLayers”, “renumberSubLayers”, “removerLayers”, “removeSubLayers”, “modifyRefCoordSys”, “modifyPositionRefCoordSys”, “setTocombili”. (An advantage of this modification is that it allows to “chain” operations modifying a Result object in one single instruction.)
A few modifications in the reading of Nastran nodal vectorial Results from OP2, XDB or HDF files.
Correction of COM component “Result” class method “initZeroResult”. An “AddRef” was missing which was likely to lead to a Segmentation Fault.
The new version of the library is issued 2020/01/01:
Correction of several bugs in the reading of Samcef Results from DES/FAC files.
Support for Samcef Result codes 334, 335, 3234 and 3235 (Element strain and kinetic energies).
Correction of a few bugs in the reading of results from Samcef DES/FAC files. (Among other things, the reading of Samcef code 221 for Reaction Forces and Moments.)
Addition of “ElemsAllToCenters” to the list of possible “FromTo” parameters of the “deriveByRemapping” method in Result class. This has been done to mimic a corresponding Patran averaging method.
Addition of “CornersToElemsAllNodes” to the list of possible “FromTo” parameters of the “deriveByRemapping” method in Result class. This has been done to mimic a corresponding Patran averaging method. Note that this reinterpolation method is available for Nastran results only.
Addition of method “getResultLcInfos” to “DataBase” class.
Libraries are produced for additional versions of Python and Ruby.
New post-processing project that presents a lot of improvements wrt previous versions. (See Chapter IV.4.)
The new version of the library is issued 2020/02/09:
Small modification of the “getResultCopy” method of “DataBase” class, and of the “extractResultOnEntities” method of “Result” class. It is now possible to produce Result objects, with a selection on elements or nodes without providing a Group argument. (Check section I.1.3 for examples of valid calls and a more detailed description.)
Several methods are now proposed in “ClaLam” class for the calculation of laminate out-of-plane shear stresses. SectionII.1.6 of the CLA background manual has been deeply modified accordingly. The choice of out-of-plane shear calculation method is related to methods “setMuxMuy” And “setOopsApproach” presented in section II.4.1. (“setOopsApproach” and getOopsApproach methods are introduced in this version.)
Correction of two bugs in the ruby post-processing project presented in chapter IV.4.
Python Windows binaries are now compiled and linked with modified options. This should fix issues related to missing dynamic link libraries dependence.
The new version of the library is issued 2020/03/15:
Addition dof static iterator “each_bdfCard” to “NastranDb” class.
Addition of method “readHdf” to “NastranDb” class.
Modification of CBEAM and CBAR intermediate stations identification. They were previously identified with CbeamSt1 to CbeamSt9. Now the identification is CbeamSt01 to CbeamSt40.
Reading of CBAR element Results at intermediate stations, produced when Nastran CBARAO card is associated to CBAR elements. Correspondingly, a new “Beam Stations” Result is read from Nastran result files.
The new version of the library is issued 2020/03/17:
Correction of a big error in the reading of results from Nastran XDB files.
The new version of the library is issued 2020/07/27:
Correction of a bug in function “NastranDb.getAttachmentDictionnary()”. (A debug printing of dictionnary on standard output was done, even though not requested.)
Addition to NastranDb class of four methods meant to help in the reading of XDB file raw binary data:
getAttachmentWordsSize in section III.1.1.10.
getAttachmentSwapEndianness in section III.1.1.10.
each_xdbBinRaw in section III.1.1.10.7.
binDataToValues in section III.1.1.10.7.
The use of these methods is illustrated in section IV.2.8.
Addition of “setToCombiliPerComponent” method to the “Result” class. (See section I.4.6.9.)
Addition of the concept of “FieldCS” type of Result described in section I.4.1.5. (See also the description of modifyRefCoordSys method in section I.4.6.7.) Method assembleFieldCSFrom3Vectors is specifically devoted to the construction of this kind of Result.
Improvement of the reading of Samcef input files. (See section III.2.1.1 form more information.)
Correction of two errors in NastranDb class of COM component. (Wrong conversions of data in methods returning boolean results.)
Correction of a bug in the reading of Samcef Results.
Correction of a few other minor bugs.
The new version of the library is issued 2021/01/01. Modifications of the library:
Improvement of the management of “include” statement when Nastran models are read from BDF files, or Samcef models from DAT files. The simplification of paths to included files is better and probably more robust.
Binaries are now also produced for version 3.8* of Python and version 2.7* of ruby.
Modification of the “calcRandomResponse” method in “Post” Module. The integer and real IDs associated to “intPsdOut” results correspond to the mode ID and frequency.
Correction of the presentation of “calcRandomResponse” method in User Manual.
Correction of the sign of some bending components read from the OP2 file for CBEAM elements.
Addition of “readOp2FilteredResults” class to “NastranDb” class.
Frequency response analysis Results can now be read from Nastran OP2 Result files.
Random analysis results are read from Nastran OP2 and HDF Result files. (It seems however that Random Analysis Results are not saved in Nastran XDB files.)
Correction of a bug in the “materialId” iterators of “NastranDb” and “SamcefDb” classes.
Addition of several methods that allow the reading of Results returned in a Hash object instead of importing them into a DataBase:
“readOp22H” method in “NastranDb” class.
“readOp2FilteredResults2H” method in “NastranDb” class.
“readXdb2H” method in “NastranDb” class.
“readHdf2H” method in “NastranDb” class.
“readDesFac2H” method in “SamcefDb” class.
Correction of the “Hashin” and “Hashin_c” (2D) failure criteria, in section II.1.10.20 and in the sources.
Correction of a bug in the calculation of laminate stresses. In previous versions, ply stresses were not correct when material units did not match. All the results associated to failure criteria that depended on ply stresses were also wrong.
Correction of a bug in the calculation of laminate thermal and moisture conductivities. (Results were not correct when ply material units did not match laminate units.)
Modification of the examples:
Correction of a bug in the “Sliding” and “Gapping” criteria in “PostConnect” class of the object oriented post-processing example in chapter IV.4.
Addition of the “PullThru” failure criterion in “PostConnect” class of the object oriented post-processing example in chapter IV.4.
Programming of bolt group redistribution in the “PostConnect” class.
Addition of several tools to perform “final manipulation” of results, excel extraction and word reporting. (See sections IV.4.3 and IV.4.4.)
The new version of the library is issued 2021/03/28. Modifications of the library:
In Python library, method “NastranDb.writeGroupsFromPatranSession” is renamed “writeGroupsToPatranSession”.
Iterator “each_bdfCard” has been modified in such a way that all intermediate real values read from Nastran BDF file are stored in double precision real values until the production of iterator values. This reduces the loss of accuracy in variables read from BDF files when large field format is used.
Correction of “writeNastranCardToVectStr” and “writeNastranCardsToVectStr” methods in Python library.
Small modification in the “readOp2” method in NastranDb class to allow the reading of Autodesk’s Inventor Nastran results.
Better distinction between RBE (Rigid Body Elements) and MPC (Multi Point Constraints) is now done. Therefore, the behaviour of several methods is modified and user needs to adapt its post-processing scripts.
Correction of a bug in composite failure criteria “Hashin_c” and “Hashin3D_c”.
Correction of a bug in the reading of HDF CWELD element stress or strain Results.
| Old Method | New Method | Comments |
| Methods in “Group” class
| ||
| each_mpc | each_rbe | method is renamed |
| NbrMpcs | NbrRbes | method is renamed |
| Methods in “NastranDb” class
| ||
| getNbrRbes | NbrRbes | Becomes an attribute “getter” |
| NbrMpcs | New method | |
| getMpcNodes | getRbeNodes | for rigid body elements |
| getMpcDependentNodes | getRbeDependentNodes | for rigid body elements |
| getMpcIndependentNodes | getRbeIndependentNodes | for rigid body elements |
| getMpcNodes | getMpcNodes | for MPC/MPCADD cards |
| getMpcDependentNodes | getMpcDependentNodes | for MPC/MPCADD cards |
| getMpcIndependentNodes | getMpcIndependentNodes | for MPC/MPCADD cards |
| fillCard | fillCard | RBE and MPC cards are distinguished |
| fillCards | new method | |
| each_mpcId | New method | |
| Methods in “SamcefDb” class
| ||
| getNbrRbes | NbrRbes | Becomes an attribute “getter” |
The new version of the library is issued 2021/07/30. Modifications of the library:
Correction of a bug in the reading of Shell Moments from HDF files for random analysis. The modification of bending components sign has been removed.
Correction of a bug in the reading of ILSS failure indices from HDF files.
Correction of a bug in the reading of beam stations from Nastran stress/strain in CBAR elements from XDB files.
Addition of a few checks to prevent segmentation faults when attempting to read Results from Nastran HDF5 files without first loading HDF5 dll library.
Harmonisation of the integer and real IDs associated to Results read from Nastran OP2, H5 and XDB files. (In general, former OP2 reading is chosen as reference.)
Correction of a bug in “readDesFac2H” method in “SamcefDb” class.
The new version of the library is issued 2022/01/01. Modifications of the library:
Correction of a bug in the reading of Grid Point Forces from Nastran OP2 files. (Previously, results were not correct for models containing CROD elements when the option “RIGID=LAGR” was used.)
Correction of a bug in Python extensions: a “Py_INCREF” has been added to all the methods returning a borrowed reference to Python object. (All methods of “Result” class returning the object wer affected by the bug.)
In “DataBase” class, correction of a bug in the writing of formatted GMSH files.
Correction in a regression in NastranDb class. MAT4 and MAT5 material types are now again supported in the conversion to CLA materials.
Reading of real format accelerations and velocities from Nastran XDB files.
Reading of Nastran SOL107 and SOL159 results from NASTRAN HDF5 files.
Correction of a bug for the reading of CBEAM element stress/strain from NASTRAN HDF5 file.
Some reworking of the sources to prevent unwanted compilation warnings. This has been an opportunity to fix some issues that might become a bug with some compilers.
The new version of the library is issued 2022/08/15. Modifications of the library:
Programming of the reading of nonlinear Results from Nastran HDF5 result files.
Modifications and corrections of the naming of subcases for nonlinear Results. (For example, for Nastran CGAP and CBUSH elements.)
Addition of several methods for the “raw” reading of datasets from Nastran HDF5 Result files. (See section III.1.1.11.)
In .NET assembly, “FromTo” and “Method” arguments have been swapped in the “Result.deriveByRemapping” method. (Considered as the correction of a bug;)
Some optimization of the “keys” and “values” classes and their storage in “Result” objects.
Addition of “interaction” predefined criteria that should ease the programming of interaction between several failure criteria. (See sections X.D.1.6 and IV.2.4.3.)
Also a few corrections in User Manual.
The new version of the library is issued 2023/01/01. Modifications of the library:
Addition of a new “Interaction_abg_N_SR” predefined criterion. (See sections X.D.1.6 and IV.2.4.3.)
Correction of a few minor bugs.
The ruby post-processing example is modified as follows:
For the connections, one adds the calculation of a bolt failure criterion according to method presented in NASA-STD-5020 B [otNCE21]. For the calculation, one uses new “Interaction_abg_N_SR” predefined criterion introduced in section X.D.1.6.
The definition of data for the post-processing of connections in ruby project is done by reading “Interfaces.csv” CSV file. The file format and associated ruby interpretation code have been modified to increase the flexibility of data definition. (See section IV.4.2.)
For all the excel examples using COM component, the extension of excel files is changed from “.xls” to “.xlsm”.
Binaries compiled for additional versions of Python and ruby.
Also a few corrections in User Manual.
The new version of the library is issued 2023/04/10. Modifications of the library:
Correction of a bug in the Result class. (Segmentation fault occurred for some operations on Result objects with empty key-values associative container.
Correction of Python wrapping classes. Some attributes were not correctly defined.
Correction of a bug in method “getHdfAttachmentLcInfos” of .NET assembly.
Optimizations in the Result class. (Significant time saving is obtained in many cases.)
Correction of bugs in the extraction methods of Result class.
Minor improvements of the generation of Word reports in post-processing project.
Suport for the superelements.
The new version of the library is issued 2023/08/14. Modifications of the library:
For the reading of Nastran Grid Point Forces with “RIGID=LAGRANGE” option, creation of two new Results: “Grid Point Forces, MPC Internal Forces” and “Grid Point Forces, MPC Internal Moments”.
On the other hand, the reading of Nastran Results no longer produces “Reaction Forces” and “Reaction Moments”. (These Results were previously produced when Grid Point Forces, MPC Forces or SPC Forces wer read.) The user that needs the previous Reactions can easily obtain them adding corresponding SPC and MPC Results.
A few minor corrections in the reading of Results.
Addition of Result extraction methods based on the MPCs contained in groups. The new list of available Result extraction “methods” is given in Table I.4.6 of section I.4.3.1. This modification applies to several extraction methods as getResultCopy, getAttachmentResults and extractResultOnEntities.
The BATCH files for running the examples on Windows have been updated to better considered that sources are no longer compiled with the “-static” option. You will have to adapt the environment variables to your installation.
The new version of the library is issued 2024/01/01. Modifications of the library:
Reading of Samcef Results is improved. For example, one can read buckling (stabi) results when several static load cases are processed in the same run.
Module “common:util::splitStringRE” is removed from file “COMMON/util/util.cpp”. It seems that the sregex_token_iterator is not very well supported by some versions of C++ compiler. (Nota that this method was never called.)
Correction of a bug in the reading of Shell Forces from Samcef DES/FAC files.
Correction of a bug in Nastran CQUAD8 element. (nbrCornerNodes is 4 and not 8.) This bug led to errors when exporting model in GMSH files.
Support for Nastran POINT, SPOINT and EPOINT cards. Corresponding FEM entities are considered as nodes.
MSC Nastran CPYRAM element is supported. Corresponding results can be read from OP2 and HDF5 files.
Modification of the reading of Nastran cards in free format. (Should be a little more robust.)
A few modifications in the ruby post-project:
Correction of a several bugs.
Improvement of the calculation of the bolts according to [otNCE21].
Addition of the “RSS” type of envelopes. (See section IV.4.4.)
Addition of a “PrjExcept” class for a better tracking of errors in “PostProject”. (See section IV.4.5.1.)
...
Finally, the binaries are no longer compiled with the “static” option as it lead to problems in the management of C++ exceptions. The Windows libraries are compiled on two different computers with Windows 10 and Windows 11. corresponding archives are duffixed with “w10” and “w11” respectively. Let us hope that, provided you choose the appropriate archive, this will prevent dll compatibility issues when installed on your computer.
The new version of the library is issued 2024/06/16. Modifications of the library:
Correction in the ACID for Results read from HDF5 files in NASTRAN/hdf/dispatch_nodalTR.cpp.
Correction of an error in the coordinate transformation of CBEAM element results in file NASTRAN/element/allForCS.cpp.
Correction of several bugs in the extraction of “Element forces” , “Stress” or “Strain” Results from HDF attachment. (Some of the extractions resulted in “Segmentation Faults” during execution of FeResPost.)
Correction of a bug in the naming of random load cases read from HDF result files.
In “NastranDb” class, harmonisation of the extraction of Results from XDB and HDF files.
Correction of a bug in Python iterators of “NastranDb” class.
Addition of a few “Py_INCREF(Py_None);” in Python wrapper functions to prevent attempts to destroy the Py_None object.
Addition of the “ElemNodePoints” location for the output of Results in GMSH file in section I.1.8.
Methods “Post.openMsgOutputFile” and “Post.closeMsgOutputFile” are no longer available. On the other hand, one adds several methods allowing the specification of output stream in which information messages are printed. (See section I.6.1 for more information.)
Modification of the management of exceptions. For ruby extension, explanation is given in section I.6.12. The management of exception with Python, COM and .NET assemblies.
Correction of a few “minor” bugs.
The new version of the library is issued 2024/08/24. Modifications of the library:
Addition of optional parameter “NasParam” to the “readOp2” methods of NastranDb class. Using this parameter allows to fix some issues in the reading of OP2 IFP tables. (Table formats depending on version of Nastran.) Specifically, it has been done to solve problems when reading MAT2 and MAT9 IFP tables. Remember however that reading the model from an OP2 file is not recommended!
In Python, COM and .NET: correction of three “readOp2*” methods: the scanning of “What” parameter has been removed.
For rigid body elements, support for ALPHA and TREF fields has been added to allow compatibility with recent versions of MSC Nastran. A few bugs have been fixed in these RBE elements.
Modification of “ElemCenter” location for the CBUSH element. It now corresponds to the spring-damper location. It no longer corresponds to the middle of grids A and B.
Several corrections have been done in the manual and a few examples illustrating new capabilities are presented. The description of ruby post-processing projects in chapter IV.4 has been improved:
For example, a more detailed description of the different “post” classes is given, with Tables describing the object construction parameters.
This was the occasion to improve the programming of these classes and restore coherence between the constructions of different objects. This means that the “post” classes presented in the examples are modified and the construction of these objects are modified accordingly.
The “PostConnect” class of the post-processing project is significantly modified. It now allows a the calculation of connections using Beam Forces and Beam Moments from CBUSH, CBAR or CBEAM elements.
In ruby post-processing project, the VBA of “reportToExcelAndWord.xlsm” excel workbook has been modified to prevent some exceptions depending on the Windows or Microsoft Office configuration.
[eEL94] L. Landau et E. Lifchitz. Physique Théorique, Volume 2 : Mécanique. Cinquième edition, 1994.
[Gay97] Daniel Gay. Matériaux Composites. Hermès, 1997.
[Hex22] Hexagon, editor. MSC Nastran 2022.4 Superelements and Modules User’s Guide. Hexagon, 2022.
[LL13] L.D. Landau and E.M. Lifshitz. Statistical Physics: Volume 5. Number vol. 5. Elsevier Science, 2013.
[LLK86] L.D. Landau, E.M. Lifshitz, A.M. Kosevich, J.B. Sykes, L.P. Pitaevskii, and W.H. Reid. Theory of Elasticity: Volume 7. Course of Theoretical Physics. Elsevier Science, 1986.
[Nas05] MSC.Access User’s Manual. MSC.Software Corporation, 2005.
[otNCE21] Office of the NASA Chief Engineer. NASA-STD-5020-B, Requirements for the Threading Fastening Systems in Spaceflight Hardware. Nasa Technical Standard. NASA, 2021.
[Pal99] Markku Palanterä, editor. Theoretical Background of ESAComp Analyses, Version 1.5. april 1999.
[Rey04] Michael Reymond. MSC.Nastran 2005, DMAP Programmer’s Guide, volume 1. MSC.Software Corporation, 2004.
[Sof04a] MSC Software, editor. MSC.Nastran 2004, Reference Manual. MSC.Software Corporation, 2004.
[Sof04b] MSC Software, editor. MSC.Nastran 2005, Quick Reference Guide. MSC.Software Corporation, 2004.
[Sof10] MSC Software, editor. MD/MSC. Nastran 2010, Dynamic Analysis User’s Guide. MSC.Software Corporation, 2010.